湿热环境中含脱层复合材料层合板的界面裂纹扩展
2023-01-12夏飞薛江红何赞航金福松
夏飞, 薛江红, 何赞航, 金福松
(暨南大学 力学与建筑工程学院, 广州 510632)
纤维增强复合材料是由高强度、高刚度的纤维作为增强材料,与基体材料进行模压、缠绕等方式形成宏观上具有新性能的材料。 相对于传统材料,纤维增强复合材料具有比强度高、耐腐蚀性好、可设计性好等优点,在机械化工、航空航天等众多领域得到广泛应用。 对于复合材料层合结构,在加工使用过程中极易出现损伤,层间脱层是复合材料层合板壳结构的一种常见缺陷或损伤形式,主要发生在层板的界面上。 层合板壳结构发生脱层扩展的根本原因是脱层前沿处的应力累积,由于前沿处应力场分布的奇异性,作为层间断裂韧性表征量的临界应变能量释放率得到广泛应用[1]。 同时,环境中温度和湿度的改变也会在复合材料层合板内部产生湿热应力,削弱层合板的承载能力。 因此,分析湿热环境中复合材料层合板结构在压缩荷载下的非线性后屈曲、脱层扩展等力学行为,是一项极具工程意义的工作。
关于含脱层复合材料层合板壳的非线性力学研究,Chai 等[2]最先提出一维穿透脱层分析模型,研究脱层层合板的整体失稳。 刘述伦等[3]讨论了含有贯穿脱层复合材料层合板的力学性能与湿度和温度之间的关系,并给出了屈曲问题的解答。 周宇等[4]考虑含纤维搭桥的影响,建立了用挠度和应力函数表示的正交各向异性材料矩形脱层屈曲非线性方程组。 李萍等[5]考虑接触效应,研究了单向铺设的层合梁的非线性后屈曲路径。Köllner 和Völlmecke[6-7]提出了一种分析模型,该模型仅用广义坐标就可模拟层合板的后屈曲行为和分层损伤。 文献[2-7]都是基于经典板壳理论,忽略板在横向界面处由于剪力引起的横向剪切变形,由于层合板/壳对横向剪切变形很敏感[8],由此发展出适用于中厚板的剪切变形理论。 基于一阶剪切变形理论(first order shear deformation theory, FSDT)及分层理论,Nikrad 等[9]研究了含集合缺陷的复合材料层合板的后屈曲行为,并与有限元结果进行了对比验证。 同样考虑FSDT,Wang等[10]研究了含椭圆分层的复合材料层合板的压缩破坏,所建立的模型与实验结果一致。 Shabanijafroudi 和Ganesan[11]则给出了一种新的脱层模型数学建模方法,与有限元的算例验证中证明该方法可以降低求解的计算量。
复合材料层合板的脱层扩展一般分为:Ⅰ型张开、Ⅱ型滑移和Ⅲ型撕裂。 Pereira 和Morais[12]建立梁模型计算能量释放率,并结合实验和虚拟裂纹闭合技术,分析了复合材料层合结构的Ⅰ+Ⅱ混合型层间断裂。 郑伟玲和郑龙席[13]发展了一种通过位移来计算3 点弯曲梁模型中裂纹能量释放率的方法。 任雷和盛冬发[14]建立了二维有限元模型,分析了单向纤维增强复合材料板I 型裂纹的尖端应力场。 Tay 等[15]综合使用扩展有限元(extended finite element method, XFEM)和内聚力单元(cohesive element, CE),模拟了复合材料渐进损伤过程3D 分层和基体开裂及两者之间的相互作用。 邓健等[16]基于经典层合板理论及双线性黏聚区本构关系,提出一种I-II 混合型断裂的裂纹扩展理论模型。
文献[12-16]关于界面裂纹的研究大多基于实验和有限元仿真,从模型受载和边界的形式来看,研究主要集中于双悬臂染(double cantilever beam, DCB)、端部切口弯曲(end notched flexture,ENF)、 混 合 模 式 弯 曲(mixed mode bending,MMB)层合试件,对于承受面内荷载作用的含初始脱层层合板裂纹扩展的理论研究还不多。 为了深入探讨含脱层复合材料层合结构的承载能力,Xue 等[17-19]开展了系列研究,详细讨论了接触效应与模态解的关系,并提出由于接触的存在,含脱层层合板呈现的是整体一致的屈曲模态和后屈曲变形,在面内压缩荷载作用下,含脱层层合板发生Ⅱ型面内滑移扩展,研究表明,脱层界面发生扩展的主要原因是层间剪应力的累积,也与后屈曲阶段横向剪力和剪切变形的增加有关。 本文基于FSDT,分析了承受轴压作用的复合材料层合板在脱层界面的裂纹扩展行为。 建立含脱层复合材料层合板的四分区模型,考虑环境湿热和脱层界面的接触效应的影响,推导脱层复合材料层合板在湿-热-力载荷作用下的总势能,并求解非线性后屈曲的控制方程。 结合断裂力学中的断裂准则,给出脱层扩展的能量释放率表达式,并进一步求得脱层界面发生扩展时的临界压缩载荷。 通过开发MATLAB 程序代码进行数值计算,讨论了脱层几何尺寸和湿热环境对复合材料层合板承载能力的影响。
1 基本理论
1.1 数学模型
考虑一含初始贯穿脱层的复合材料矩形中厚板,其长为a、宽为b、高为h,由厚度为h0的单层板以一定角度铺设黏合而成。 边界条件为四边简支,左右两侧受轴向压缩荷载Nx的作用。 为便于分析,将脱层复合材料层合板模型简化为可计算的四分区数学模型,如图1 所示。 脱层长度为L2,与上表面的距离为h2,脱层左前沿与左边界的距离为L1,由此将模型分为4 个层板,分别记为子层合板Ω(i),i=1,2,3,4。 随着纵向压缩载荷的增加,脱层前沿裂纹将扩展δni,各子层合板的边界及尺寸也随之发生变化。
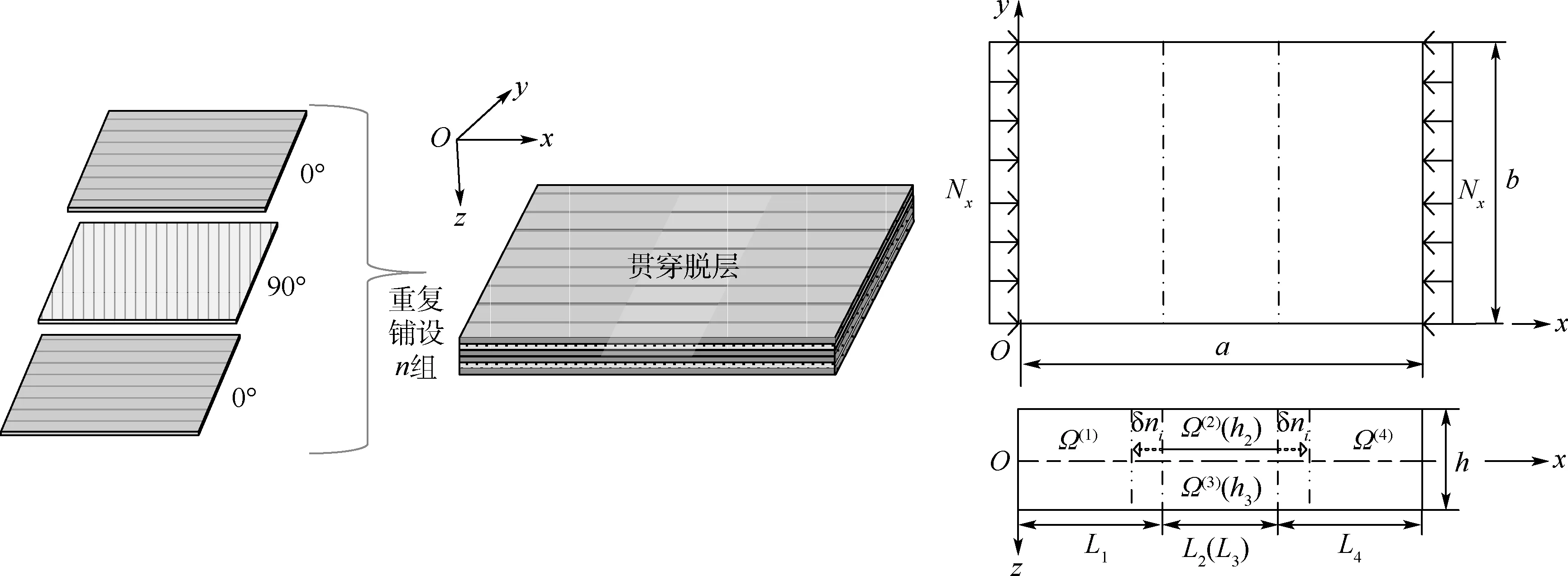
图1 含脱层复合材料层合板的四分区模型Fig.1 Four region modeling of delaminated composite laminates
假设层合板在发生变形时y-z横截面和x-z横截面的转动角度分别为和,则考虑FSDT的层合板的位移场u(i)、v(i)、w(i)为

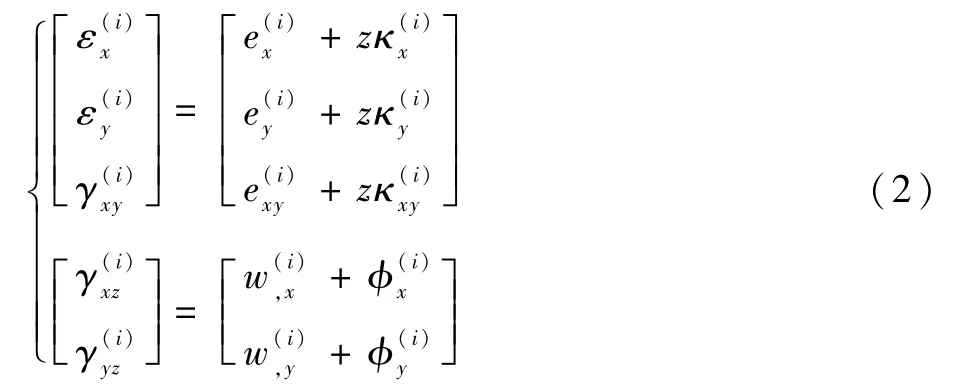
式中:

在湿热环境中,层合板的应力场分布受到湿热力和机械力的共同影响,用[N(i)]E(、、)E和[]E(、、)E分别表示层合板的总薄膜内力和总弯矩,即
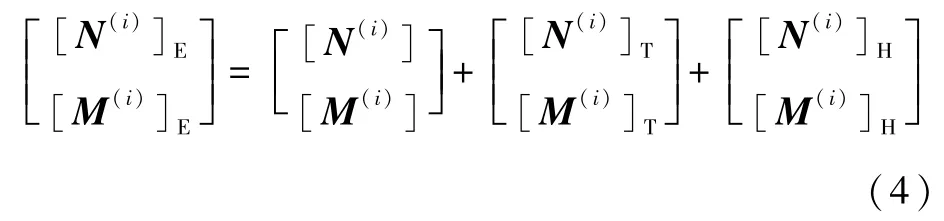
式中:[N(i)]和[M(i)]分别为机械内力和内力矩;[N(i)]T和[M(i)]T分别为热内力和热力矩;[N(i)]H和[M(i)]H分别为湿内力和湿力矩。
湿热内力和内力矩为[20]


设[σ]为应力分量,[ε]为应变分量,则有
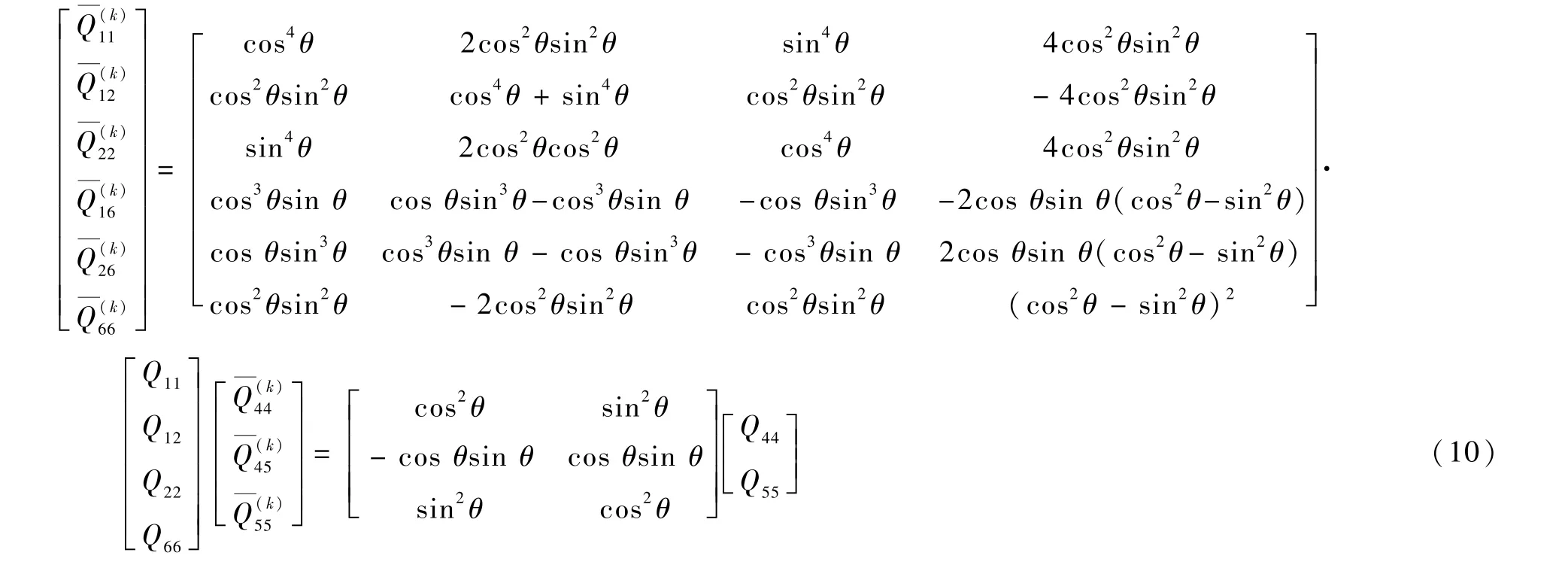
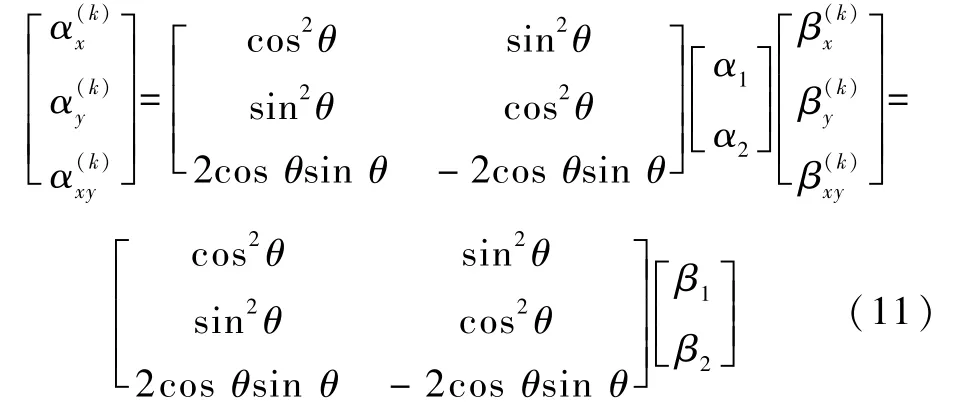
其中:θ为铺设角;α1、α2为热膨胀系数,β1、β2为湿膨胀系数,均由实验测得;单层板的折减刚度系数的各分量为
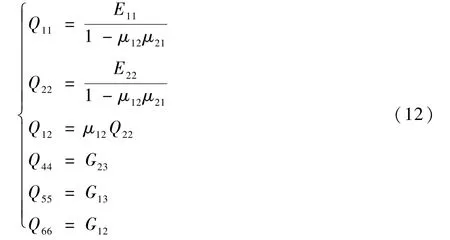
式中:E11、E22分别为材料在1、2 弹性主方向上的弹性模量;G12为材料在1-2 平面内的剪切弹性模量;μ12和μ21为泊松比。
由式(2)和式(9),得到湿热环境中正交对称铺设的层合板的本构关系为


层合板在发生面外弯曲变形时,脱层界面处的上子板Ω(2)和下子板Ω(3)之间受到一对相互作用的接触力q*作用,导致上下子板Ω(2)和Ω(3)之间载荷的重新分配。 用线弹簧模型模拟层间接触力与上下子板弯形w(2)和w(3)的关系[17]:

式中:接触系数ke为

1.2 能量分析
静力平衡状态下,含脱层复合材料层合板所受的外力功为
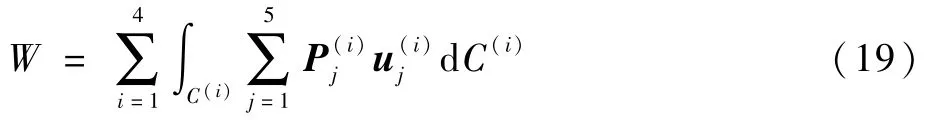
式中:C(i)为子板Ω(i)的边界;和分别为子板Ω(i)边界上的广义外力和广义位移,可以表示为
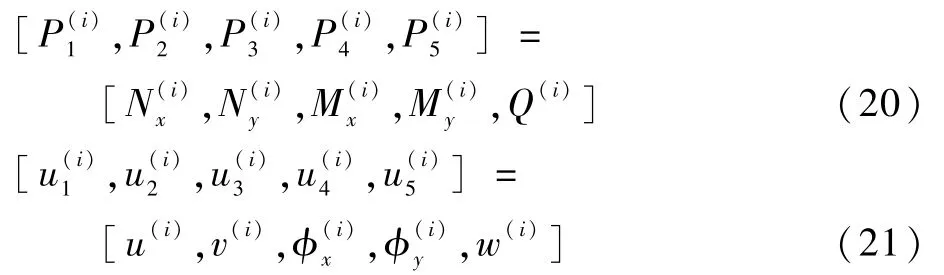
在湿-热-力载荷的共同作用下,含脱层复合材料层合板内的弹性势能为
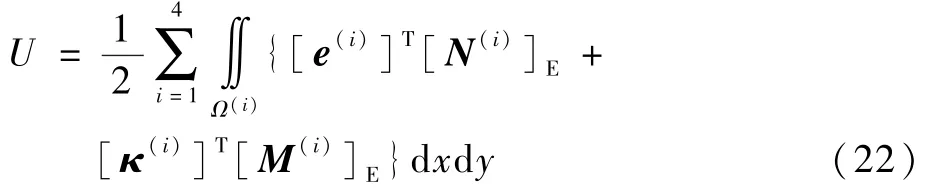
设脱层发生的虚扩展为δni,系统内总势能改变量的变分形式δΠ为
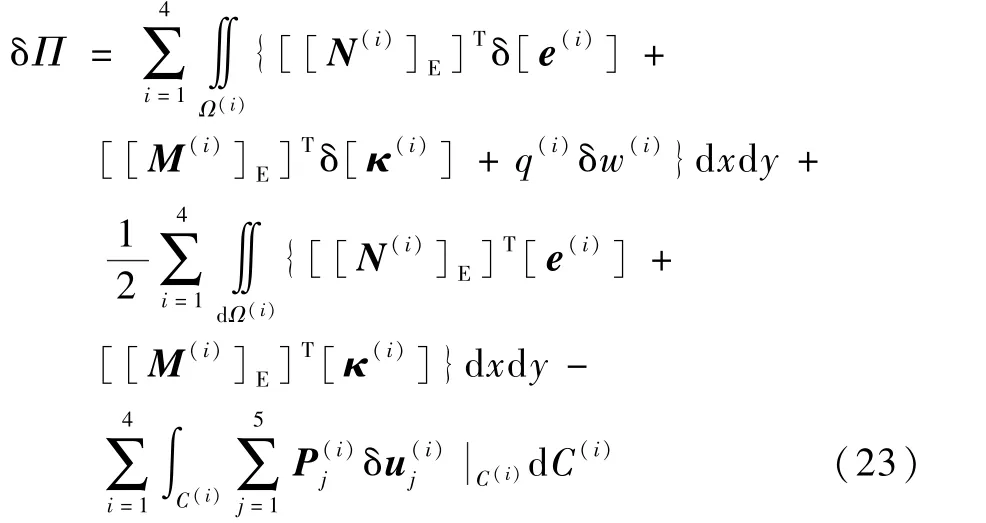
本文分析的是受轴向压缩载荷作用的复合材料层合板,考虑到复合材料层合板较弱的层间属性及初始脱层的存在,故假定裂纹的扩展路径是在脱层前沿处沿着层间方向发展。 根据可动边界变分原理,在动边界上的广义位移(j= 1,2,…,5)的变分形式为
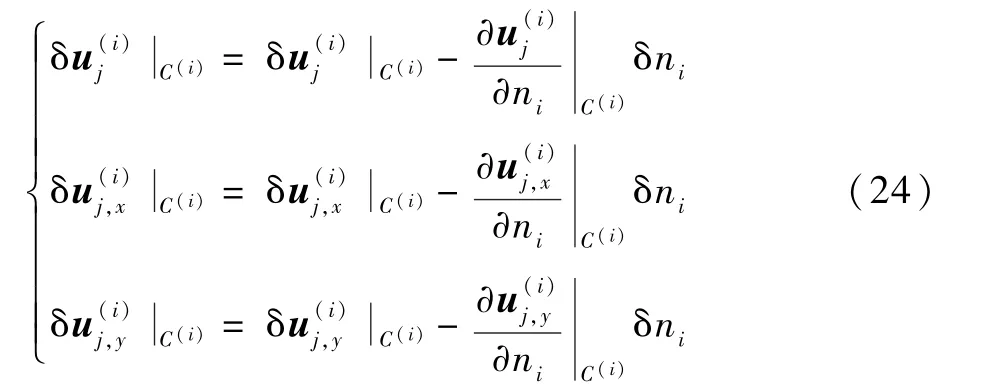
式中:δni为脱层扩展的方向,用δn表示脱层前沿边界发生正方向扩展,则有

将式(24)和式(25)代入式(23)后,系统总势能改变量的变分δΠ可拆分为2 部分:

式中:
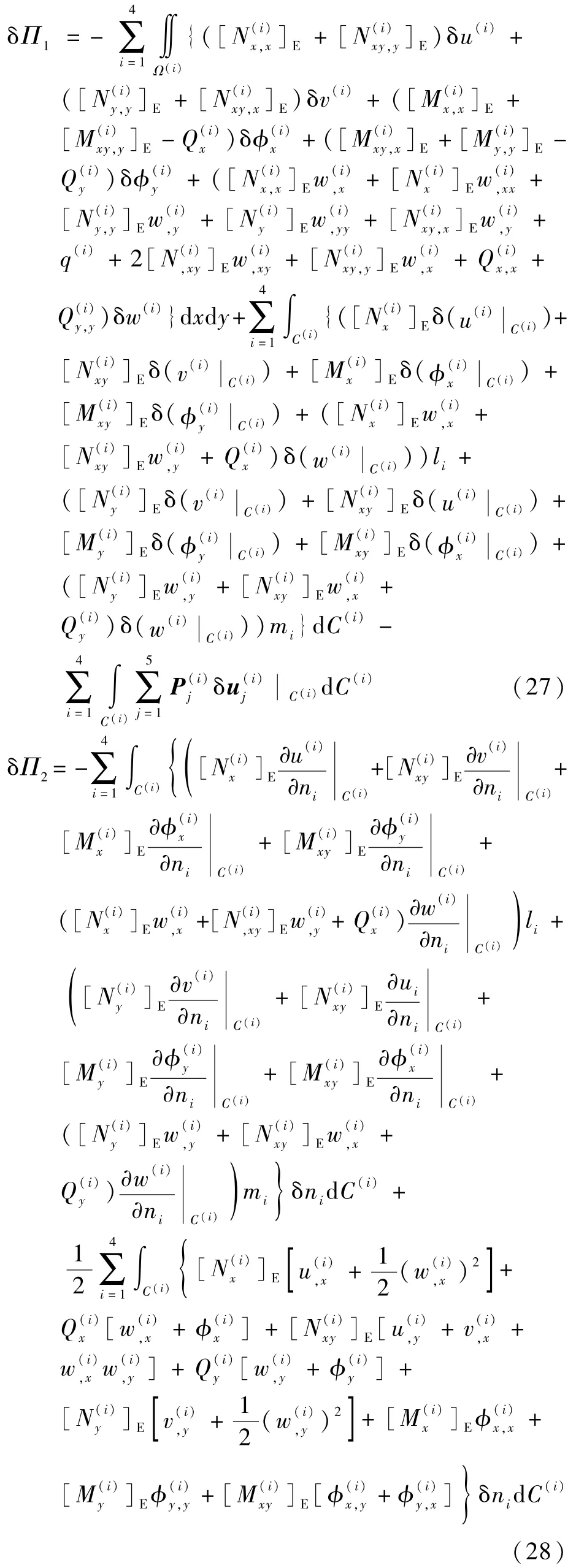
式中:li和mi分别为子板Ω(i)的边界法线在x轴和y轴上的方向余弦。 对于本文的模型,层间裂纹的扩展方向只会沿着x轴,故mi应取为0。 δΠ1是脱层边界不变时,脱层板系统的势能改变量,根据虚功原理,系统保持静态平衡的必要条件为

δΠ2为脱层板在动边界上发生扩展时的总能量变化量。 从图1 中可以看出,由于模型的对称性,层合板位移函数u、v和转角函数φx是x坐标的奇函数,转角函数φy是y坐标的奇函数,位移函数w是x、y坐标的偶函数;同时左右两边脱层前沿处的扩展能量变化相同,故脱层板在发生扩展时的总能量变化量δΠ可以简化为
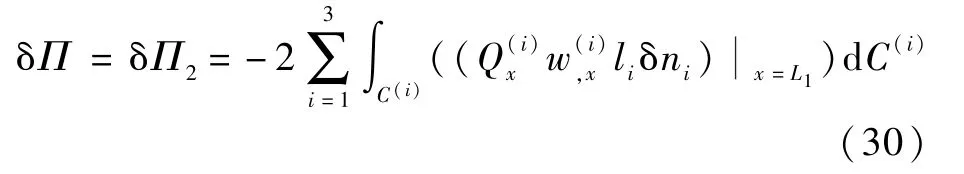
相对应的,脱层板在发生扩展时的总面积变化量为
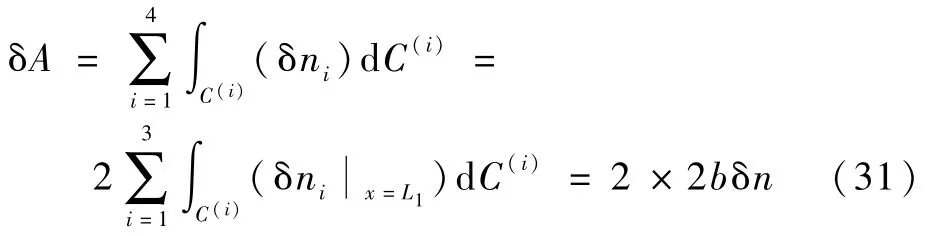
根据能量释放率的定义,本文分析的受压脱层板在脱层前沿处的能量释放率为
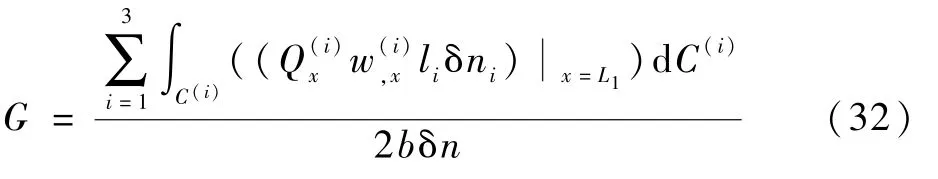
1.3 静态平衡方程及定解条件
对于承受压缩荷载作用的含脱层层合板,式(27)和式(29)中给出了脱层板在静态平衡下的基本控制方程和边界连续性条件。 根据弹性力学知识,首先引入应力函数Φ,有
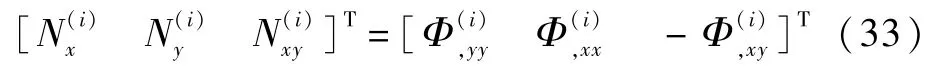
将式(33)代入式(29),得到用位移函数w(i)和转角函数和表示的脱层板的非线性控制方程组:
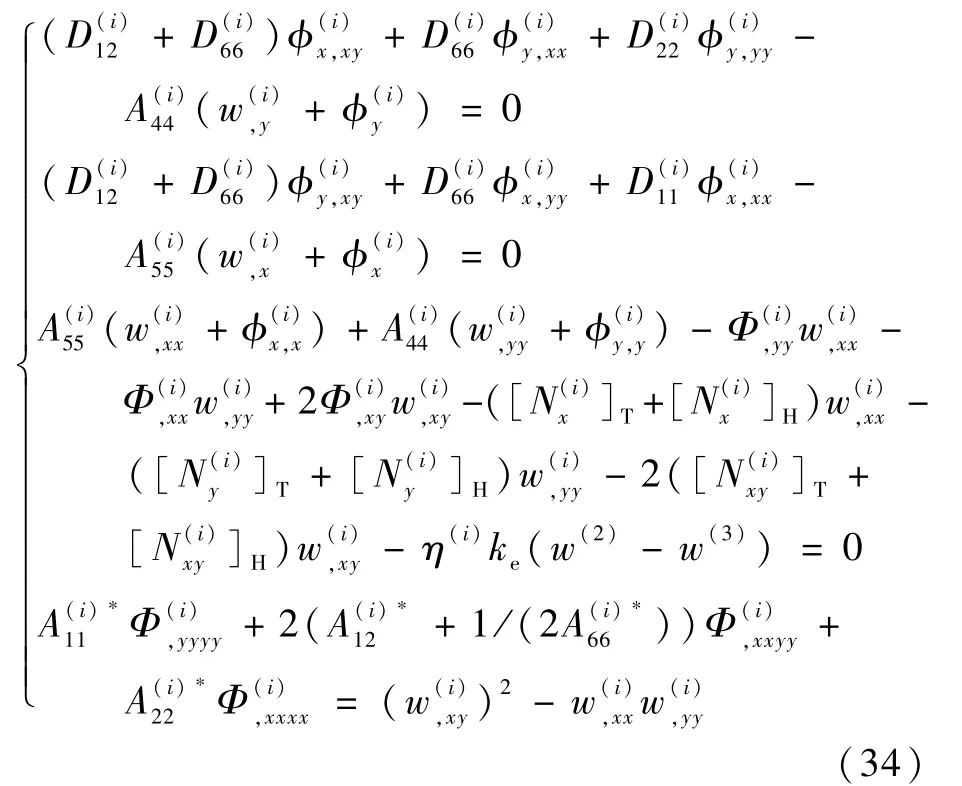
同时,脱层板的边界条件为四边简支。 结合板在脱层前沿处的连续性条件,求解上述静态控制方程组的定解条件如下。
在y=0 处,
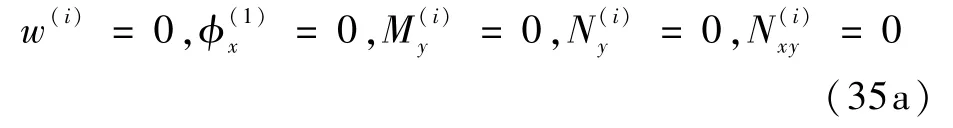
在y=b处,
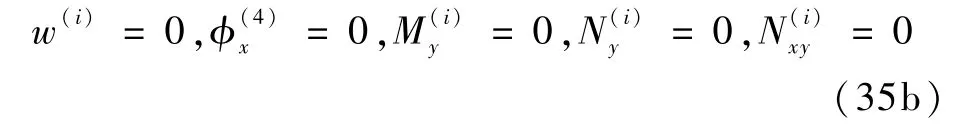
在x=0 处,
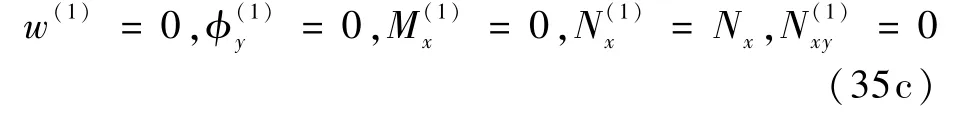
在x=a处,
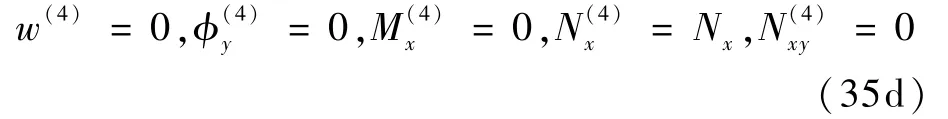
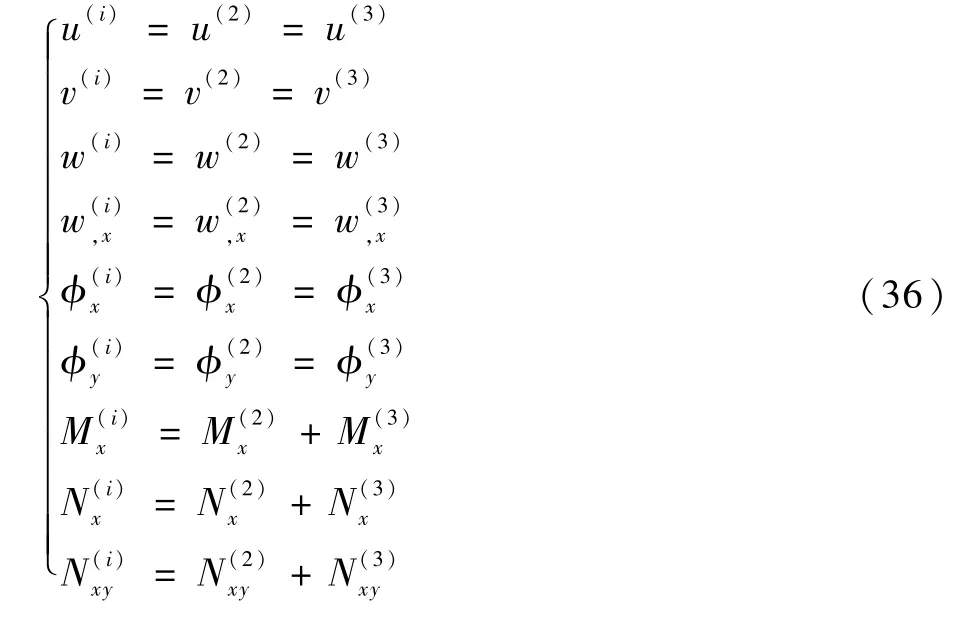
在x=L1处(i=1)和x=L1+L2处(i=4),
2 摄动求解
求解非线性控制方程式(34)的精确解比较困难,本文提供一种数值解法——小参数摄动法进行求解。 为方便摄动运算,引入如下形式的无量纲参数:

将式(37)代入式(34) ~式(36)中,得到无量纲形式的控制方程和定解条件。 选取¯w0(¯w0=
wmax/h)为摄动小参数,对式(34)中所有变量进行如下形式的摄动展开:
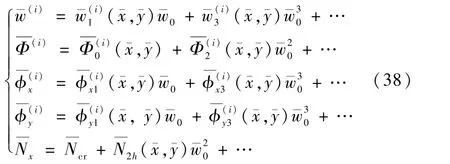
把摄动展开式(38)代入无量纲后的控制方程式(34)及定解条件式(35)和式(36)中,得到关于的多项式,根据的阶次依次提取一阶、二阶和更高阶的控制方程,并逐次进行求解。 本文主要求解前两阶方程,对应求得脱层板的屈曲解和后屈曲响应。 将式(37)和式(38)代入式(34)中,按照¯w0的阶次合并同类项,其中一阶摄动方程为

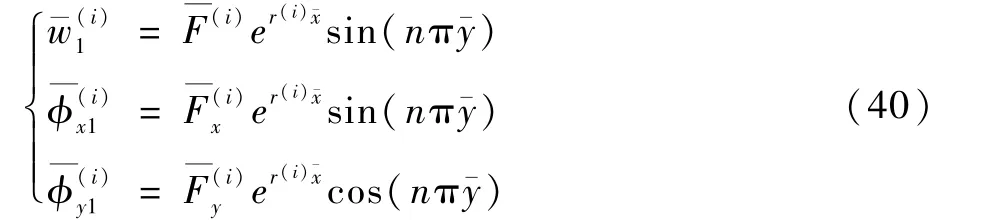
由于接触力的存在,子板Ω(2)和子板Ω(3)的控制方程是耦合方程,需要一起求解。 将式(40)代入式(39),得到
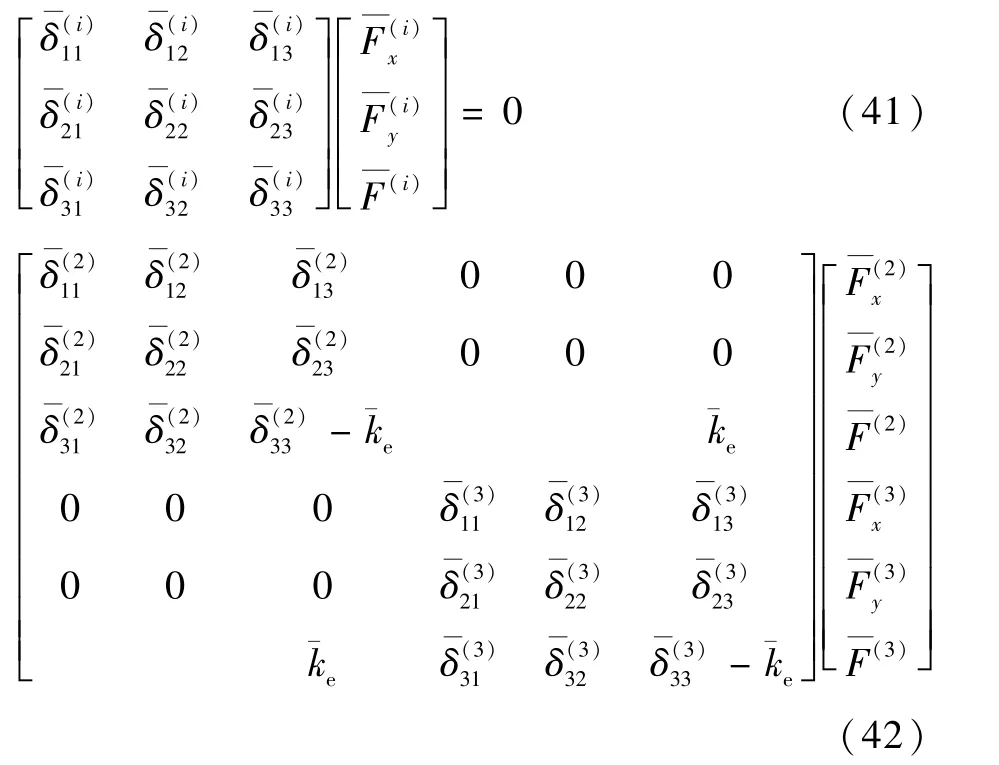
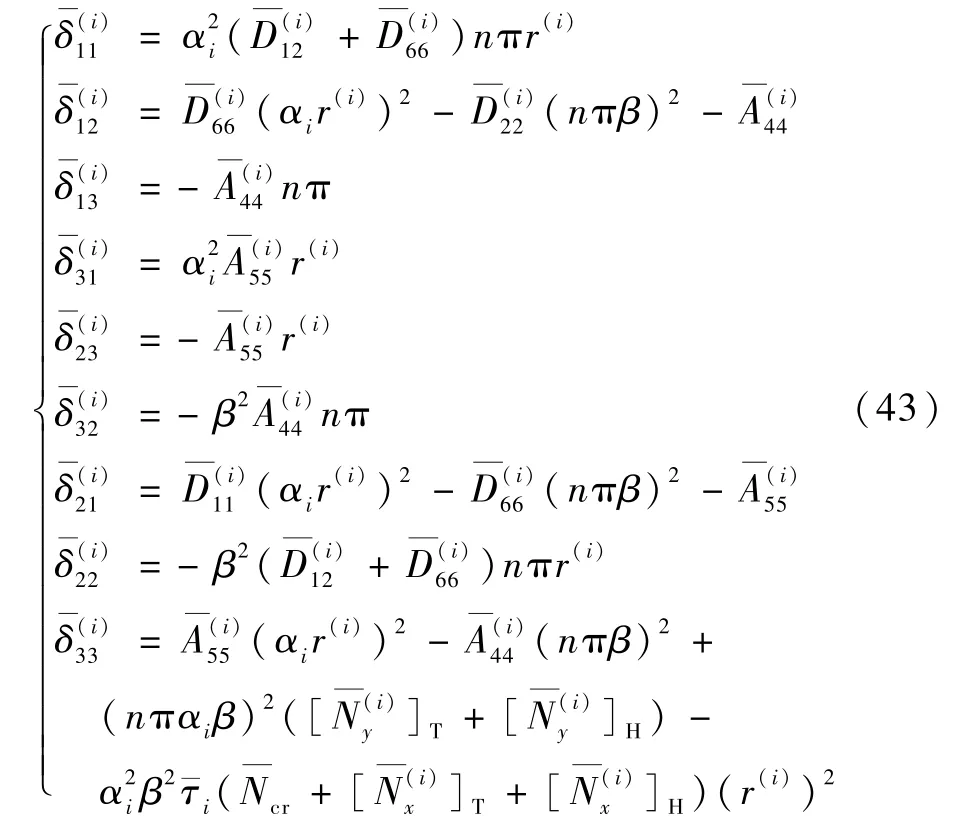
式(41)和式(42)成立的必要条件是其系数矩阵等于0,由此得到关于模态参数r(i)的特征方程:

用复数根的形式表示模态参数r(i)为
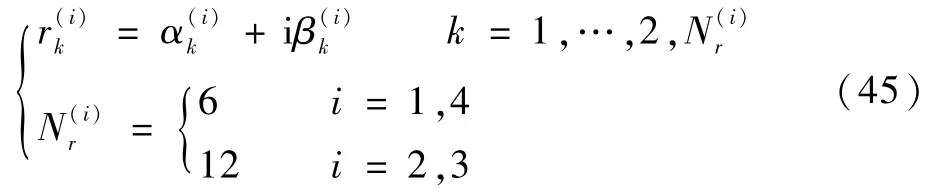


将式(46)代入式(39)的前两式,即可确定其值:
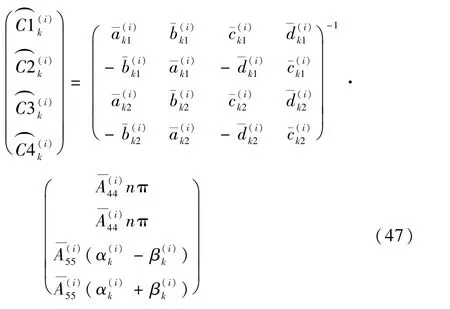
式中:
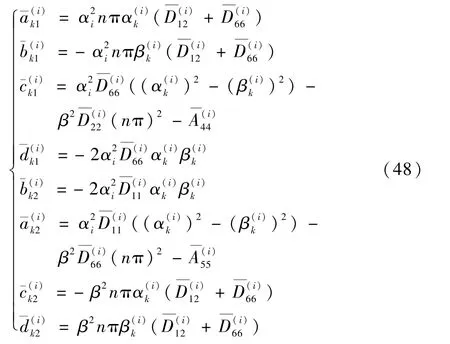
将式(46)代入无量纲后的定解条件式(35)和式(36)中,建立下面的齐次方程组:
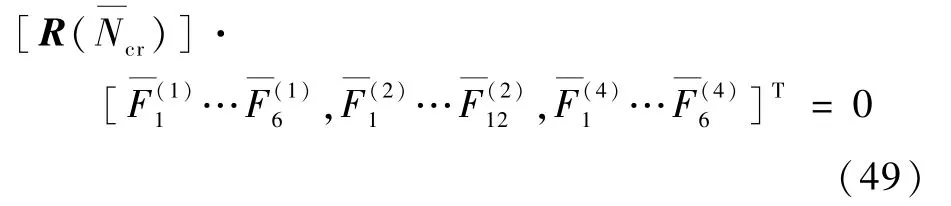
式中: [R()] 为一个24 ×24 的系数矩阵。
式(49)成立的必要条件是系数矩阵等于0,即

(2)(1/2,1/2) =1,即可求得24 个待定系数[…,从而确定式(46)。 二阶摄动方程为
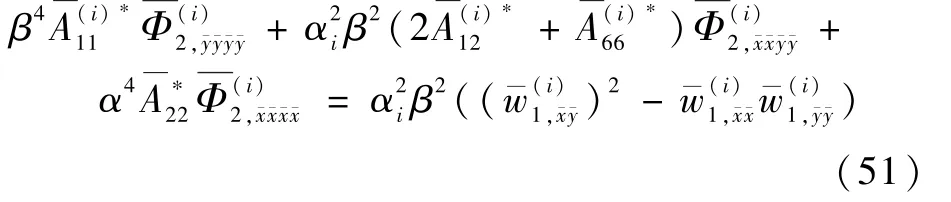
假设二阶摄动方程的形式解为

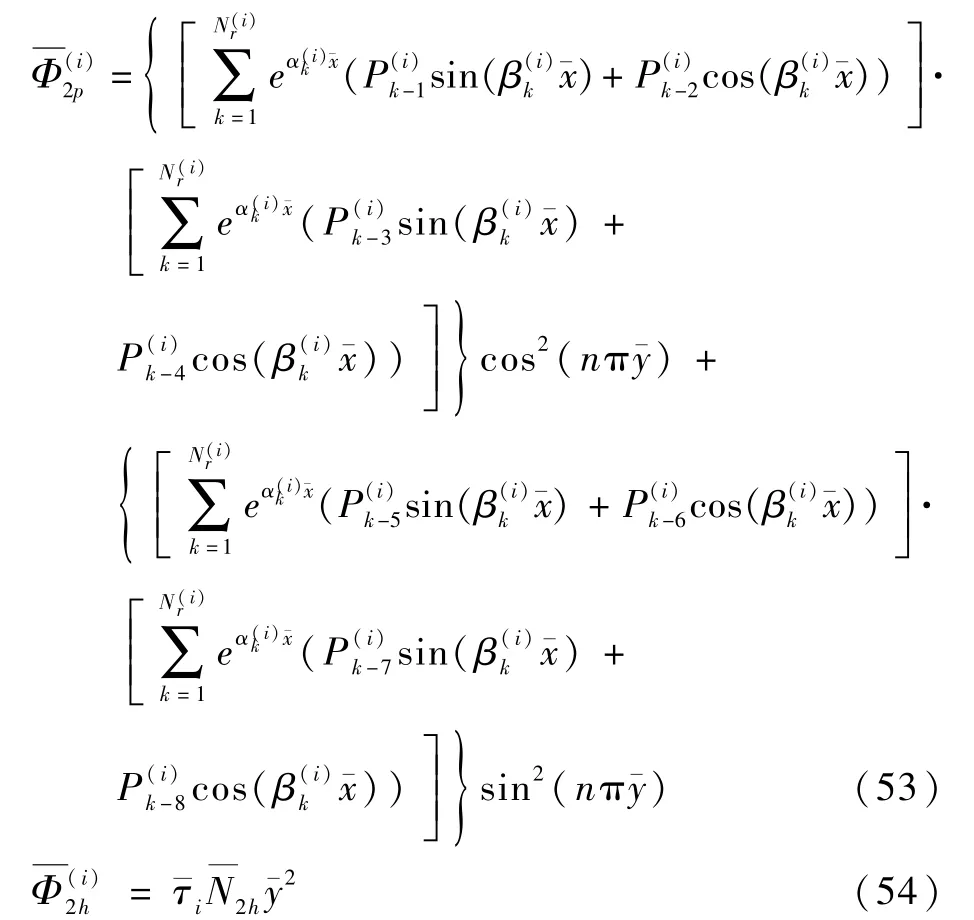
将式(46)代入式(51),并根据方程左右一一对应关系可确定式(53),其中,为相关系数。通解需要用Galerkin 方程进行求解:
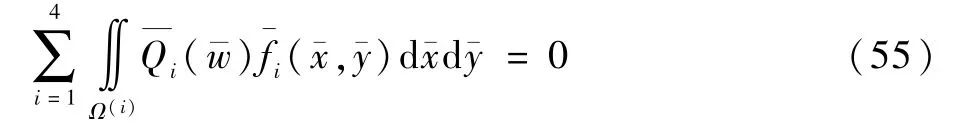
式中:
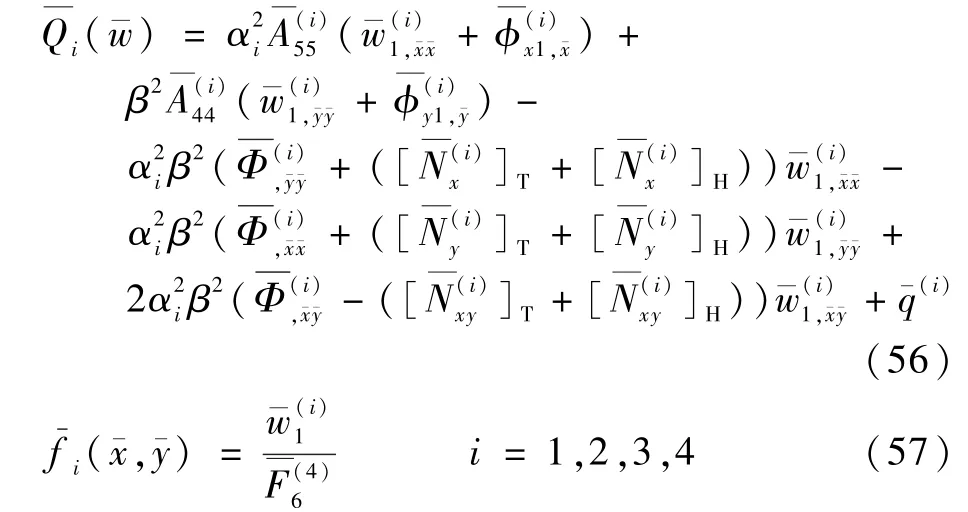
将式(56)和式(57)代入式(55)并进行简化得到后屈曲增量:
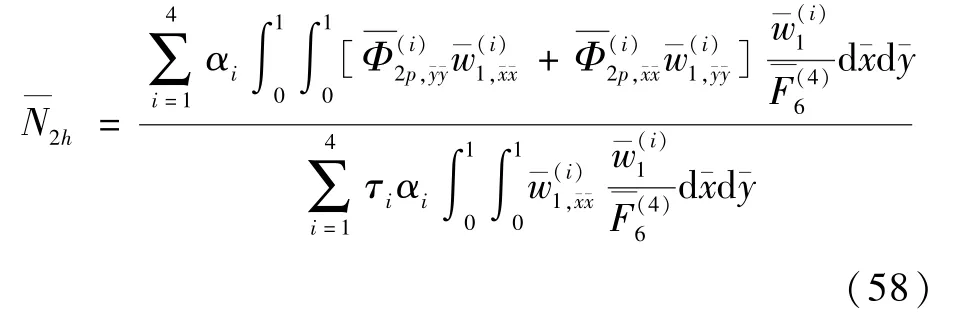
根据式(38)和式(58),可以确定脱层板在静态压缩时的后屈曲路径为

将式(38)中位移函数和转角函数的一阶摄动展开式代入式(32),得到用一阶摄动方程的解和表示的脱层板的能量释放率:
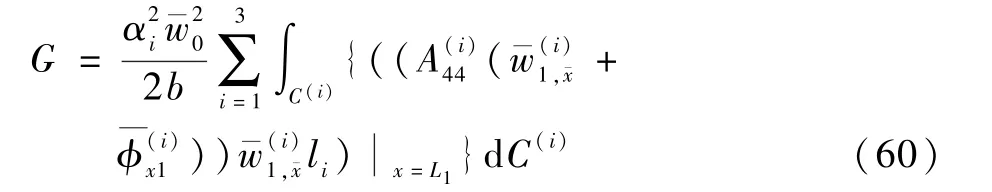
根据断裂力学的准则,如果裂纹前沿处的能力释放满足G≥Gcr,则判定裂纹发生扩展,其中Gcr为材料的断裂韧性。 结合式(60),可以推导出脱层板发生脱层扩展时的无量纲临界扩展载荷为
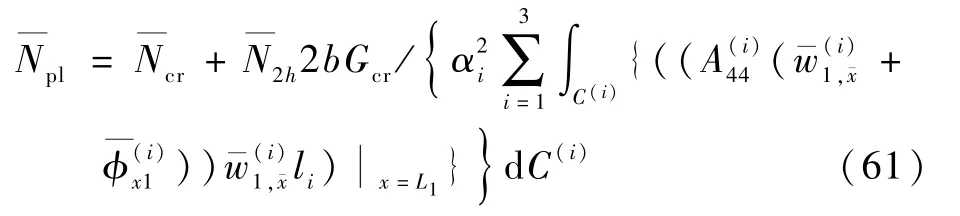
从式(32)和式(61)中可以看出,在几何尺寸和材料参数确定的情况下,脱层界面发生裂纹扩展时的能量改变δΠ主要由脱层前沿处的剪力项与横向挠度有关项决定,承受轴向压缩荷载的脱层板的Ⅱ型扩展主要发生于板的后屈曲阶段。 求解过程如图2 所示。
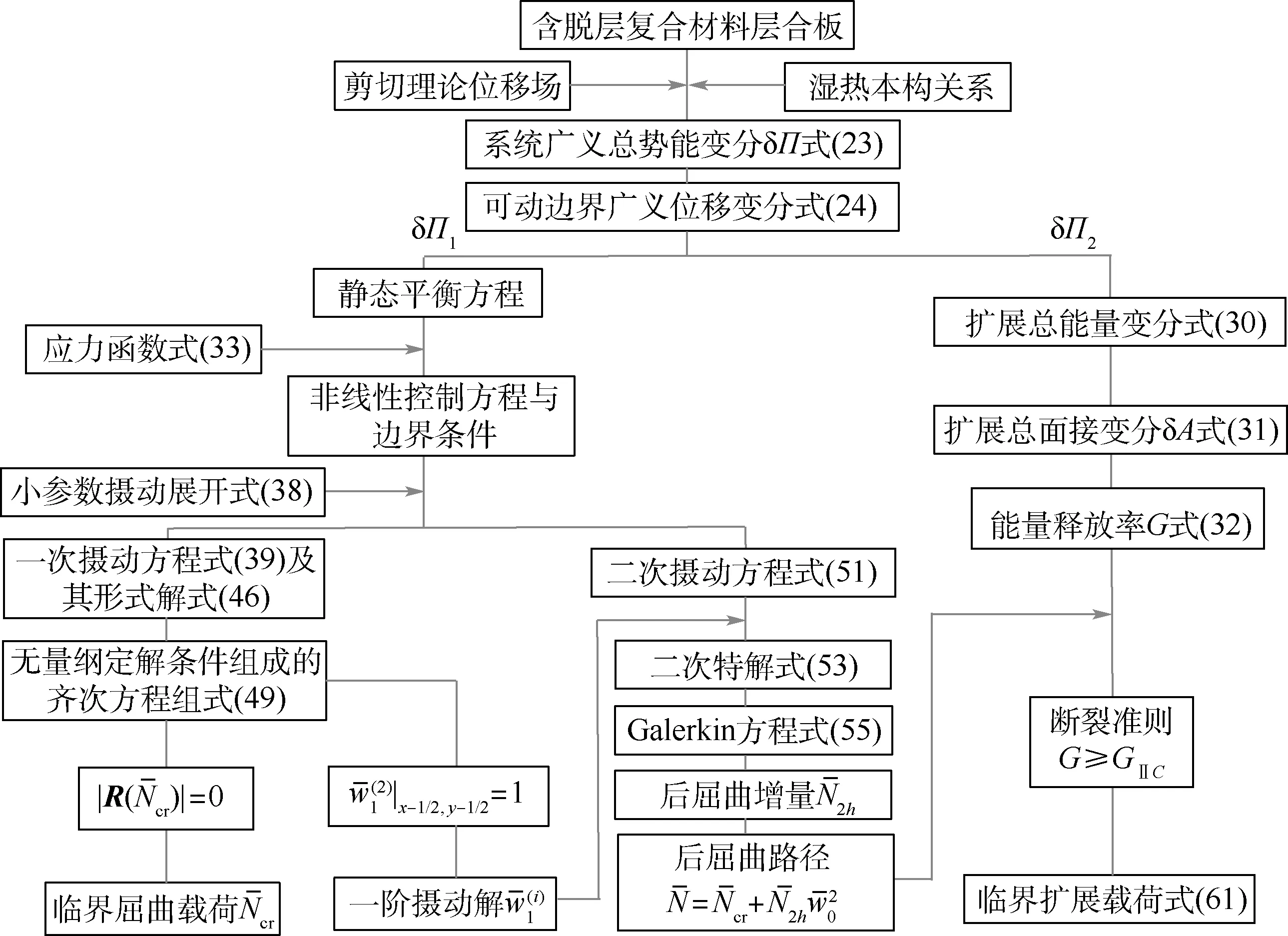
图2 求解流程Fig.2 Flow chart of solving process
3 算例分析
本文的研究对象主要为四边简支的含脱层复合材料层合板,本节对第2 节的理论推导进行了验证和讨论。 其中,算例分析中选用的材料参数[15]:E11=147 GPa,E22=10.3 GPa,G12=G13=7.0 GPa,G23=3.7 GPa,μ12=0.3,GIIC=547 N/m,α1= -0.3 ×10-6/℃,α2=28. 1 ×10-6/℃,β1=0,β2= 0. 44。 层合板的几何参数:a= 2 m,b=2 m,层合板的铺设情况,按0°、90°、0°铺设,总共60 层[0°/90°/0°]20,h0=0.002 m。
3.1 有限元分析
为了验证理论解的正确性,开发ABAQUS 有限元软件对含脱层复合材料层合板的屈曲行为进行了数值模拟。 同样采用四分区模型,在软件中使用三维空间内的可变形壳单元创建4 个层合板部件,保证板模型可以发生面外变形;然后通过装配组合及在脱层前沿连接位置设置绑定约束,使得有限元模型与理论模型一致。 在脱层上下2 个部件的接触面之间设置法向的硬接触,以防止其发生互相贯穿。 在模拟温度变化ΔT对层合板屈曲载荷的影响时,首先在静态通用分析步中计算温度改变引起的热应力分布,然后把得到的结果设置为线性摄动屈曲分析步中的初始状态,进而得出对应温度下的屈曲载荷。 整个有限元模型被划分为13 000 个S4R 单元以满足计算的精度,网格划分情况如图3 所示。

图3 有限元网格划分Fig.3 Diagram of finite element mesh partition
图4 为考虑热膨胀(ΔT=25 ℃,h2/h=0.1,L2/a=0.3)时的脱层板屈曲模态。 其中图4(a)中考虑了接触,从图4(a)中可以看出脱层板的屈曲模态是整体一致的变形模态,接触效应不可忽略,否则就会出现图4(b)中上下层板相互贯穿这样不合理的现象。 表1 列出了相对脱层深度一定(h2/h=0.2),不同相对脱层长度L2/a和温度变化ΔT情况下,有限元屈曲结果(FEM)与当前理论(FSDT)的比较,有限元模拟的屈曲结果同样进行式(37)中的无量纲处理。 从表1 中可以看出,有限元结果和理论结果较为吻合,2 种方法的差值比(Diff.)在5%之内,验证了理论推导的正确性。

表1 含脱层复合材料层合板的有限元方法与理论方法的无量纲屈曲载荷比较Table 1 Compassion of non-dimensional buckling load between FEM and present method of delaminated composite laminates
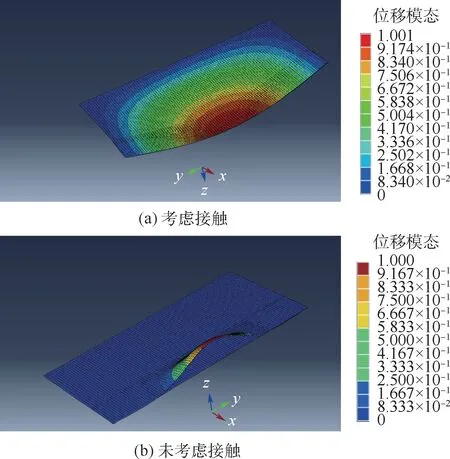
图4 含脱层复合材料层合板屈曲模态Fig.4 Buckling mode of delaminated composite laminates
3.2 文献对比
为了进一步验证理论推导结果的有效性,将本文的结果与经典层合板理论(CLPT)的解[18]进行了比较。 表2 为在不同相对脱层深度h2/h和相对脱层长度L2/a情况下,在CLPT 和FSDT 下的无量纲屈曲荷载和无量纲临界扩展荷载的对比。 可以看出,尽管脱层深度和脱层长度不同,2 种方法得到的结果的差值比均不超过7%。同时,CLPT 解总大于考虑FSDT 的解,这是由于CLPT 忽略横向剪切变形,高估了层合板的刚度和承载能力。
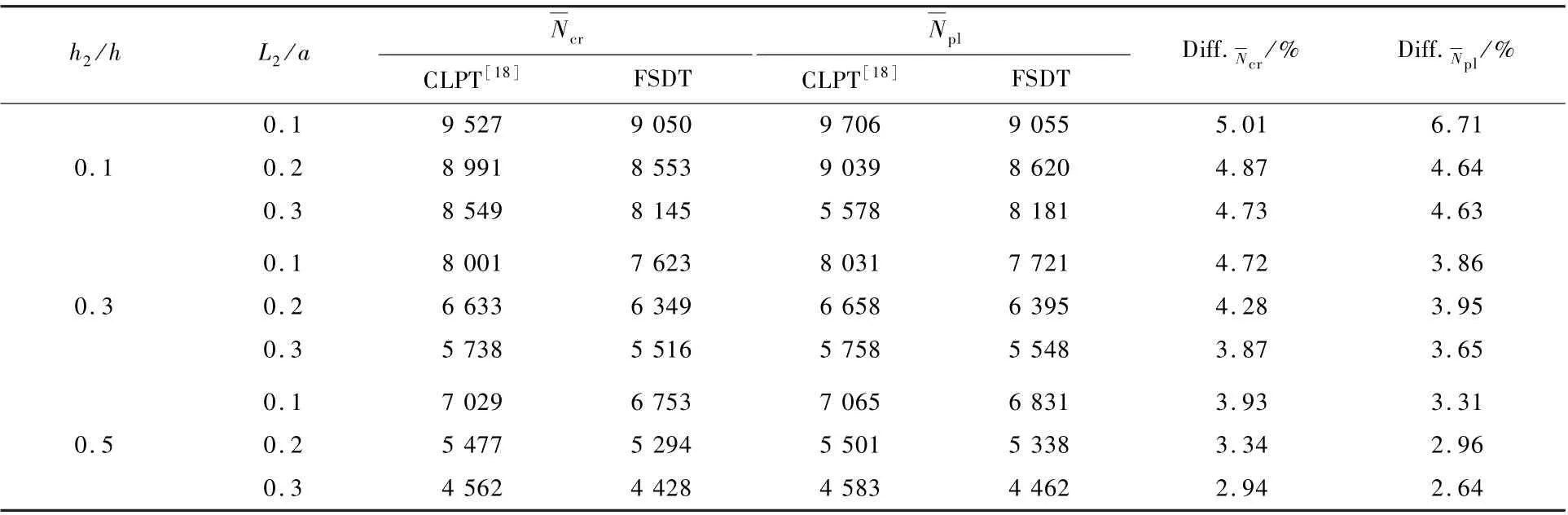
表2 含脱层复合材料层合板的经典层合板理论和剪切理论无量纲屈曲载荷和无量纲临界扩展载荷比较Table 2 Compassion of non-dimensional buckling load and non-dimensional threshold between CLPT and present method of delaminated composite laminates
3.3 脱层情况对临界载荷的影响
图5 为脱层深度(L2/a= 0. 3)和湿热环境(ΔT=25 ℃, ΔC=0.1%)一定时,脱层板的无量纲临界荷载(屈曲载荷和临界扩展载荷)随相对脱层深度(h2/h)的变化情况。 如图5 所示,随着脱层深度的增加,屈曲载荷呈现先减小后增大的趋势,在脱层位于层合板中部h2/h=0. 5时,屈曲载荷达到最小值。 临界扩展载荷也有同样的变化趋势,且总大于屈曲载荷。 在压缩载荷作用下,脱层位置越靠近中间越容易发生脱层扩展。

图5 相对脱层深度对无量纲临界载荷和的影响Fig.5 Effect of relative delamination depth on non-dimensional critical load and
图6 为脱层深度(h2/h= 0. 3)和湿热环境(ΔT=25 ℃, ΔC=0.1%)一定时,脱层板的无量纲临界荷载(临界屈曲荷载和临界扩展荷载)随相对脱层长度(L2/a)的变化情况。 由于数量级的关系,将相对脱层长度化分为3 个部分:图6(a)为L2/a=0 ~0.02,图6(b)为L2/a=0.02 ~0.2,图6(c)为L2/a=0.2 ~1。 从图6 中可以看出,屈曲载荷和临界扩展载荷均随着相对脱层长度的增加而减小。 图6(a)和图6(b)显示当脱层长度趋近于0(无脱层)时,扩展载荷急剧增加且远远大于屈曲载荷;图6(c)则相反,屈曲载荷和扩展载荷同时变化且很接近,说明脱层长度越大,脱层越容易发生扩展。 图6 的曲线趋势同时也表明脱层扩展是一个持续的过程,当静态压缩载荷达到或超过脱层板的扩展载荷时,就会导致脱层长度的增加,进而导致脱层板的承载力下降,诱发脱层发生进一步扩展,直到层合板的完全破坏。
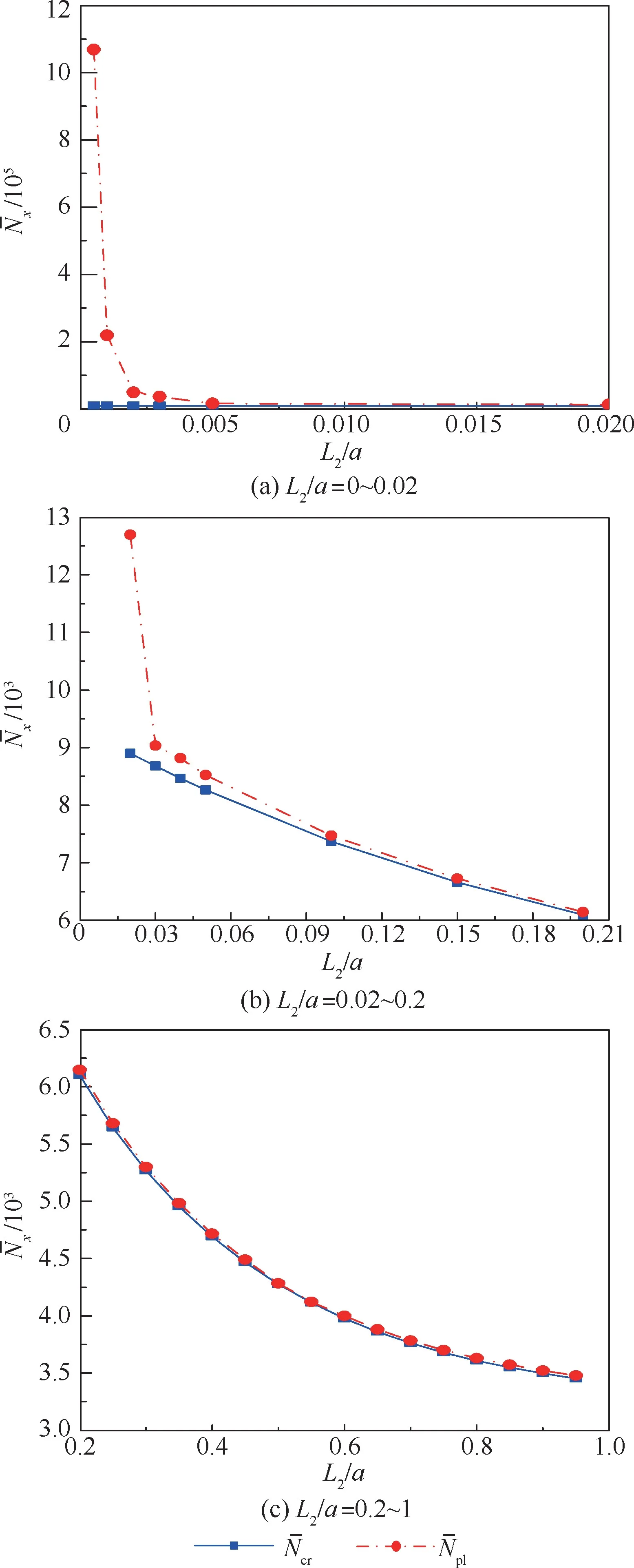
图6 相对脱层长度对无量纲临界载荷和的影响Fig.6 Effect of relative delamination length on non-dimensional critical load and
3.4 湿热环境对临界载荷的影响
图7 和图8 给出了脱层情况一定(h2/h=0.5,L2/a=0.05)时,不同温度改变量ΔT(ΔC=0%)和湿度改变量ΔC(ΔT=0 ℃)下,脱层板的承载后屈曲路径,其中¯w为无量纲挠度。 根据上面的分析,受压脱层板一旦发生扩展,会在原载荷下迅速扩展至破坏,因此图7 和图8 中各算例的后屈曲路径曲线终止于对应参数下的扩展载荷值。 图7 和图8 标注出了各种湿热情况下的无量纲屈曲载荷值和无量纲扩展载荷值,可以发现,温度和湿度的增加会极大影响脱层板的承载能力,较大的湿热变形会明显的降低脱层板的屈曲载荷、后屈曲强化载荷和临界扩展载荷。 同时,不管处于何种湿热场,脱层板都表现出后屈曲强化的特性;且随着载荷增加,脱层板在屈曲后产生的面外变形不断增加,导致层间剪力的不断累积而发生Ⅱ型脱层扩展。

图7 温度改变对无量纲临界载荷和及后屈曲路径的影响Fig.7 Effect of change of temperature on non-dimensional critical load and and post-buckling equilibrium path
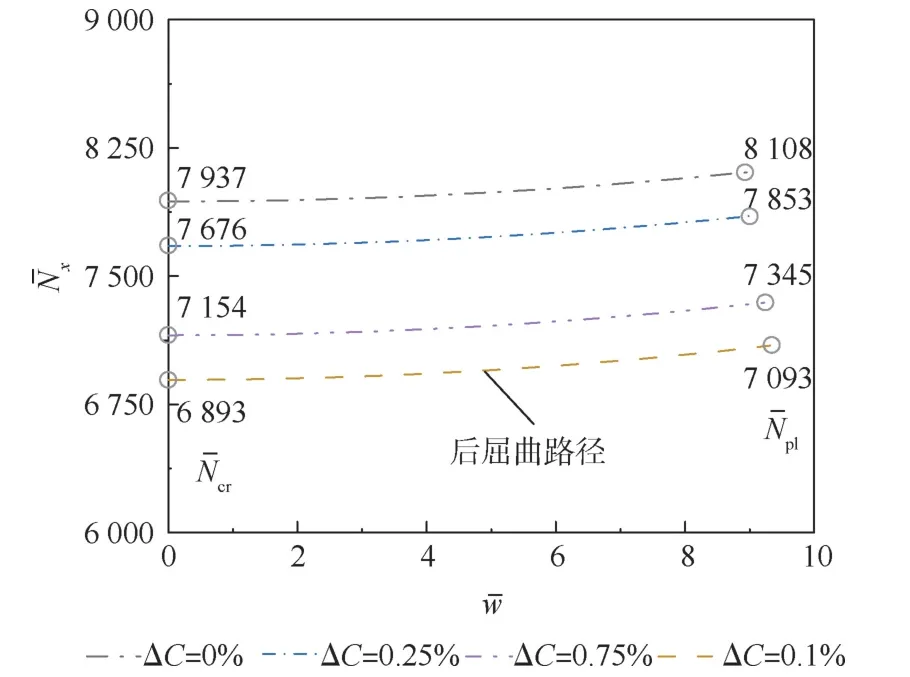
图8 湿度改变对无量纲临界载荷和及后屈曲路径的影响Fig.8 Effect of change of hygroscopic concentration on non-dimensional critical load and and post-buckling equilibrium path
4 结 论
1) 经典层合板理论由于忽略横向剪切变形,高估了层合板的承载能力,计算的屈曲载荷和扩展载荷均高于剪切理论的解。
2) 在同一湿热场中,当脱层深度越靠近层合板的中间位置或脱层长度越大时,脱层越容易发生扩展。 脱层扩展是一个持续的过程,脱层扩展导致脱层长度增加,脱层板的承载力随之下降,脱层在原压缩载荷下会继续扩展,直到层合板的完全破坏。
3) 湿热变形会显著降低脱层板的屈曲载荷、后屈曲载荷及扩展载荷。 在不同湿热场中,层合板都表现后屈曲强化的特性。
