基于图卷积网络的卷积神经网络耗时预测算法
2023-01-12李哲暘张如意谭文明任烨雷鸣吴昊
李哲暘, 张如意, 谭文明,2,*, 任烨, 雷鸣, 吴昊
(1. 杭州海康威视数字技术股份有限公司, 杭州 310051; 2. 杭州海康威视系统技术有限公司, 杭州 310051)
高清智能摄像机已成为智慧化城市管理中重要的感知来源,其含有的深度学习推理引擎能够在端侧对输入图像进行分析,向中心端系统提供高价值结构化信息。 具有深度学习推理能力的智能摄像机通常采用带有神经网络计算硬核(neural network processing unit, NPU)的片上系统(system on chip, SOC)芯片(如HISI3559)。 相对于中心端深度学习器件,边缘端的硬核加速器通常更加关注低功耗和低成本。 近年来,边缘端芯片算力有了长足的进步,智能分析输入的图像已从2 K分辨率向4 K ~8 K 高分辨率转变,智能功能需求种类也快速增长,算力和带宽瓶颈依然较为严重。 为此,芯片厂商在电路与编译器设计时采用了多种优化措施,包括权重与激活量化[1-2]、算子融合[3]、权重裁剪[4-5]、轻量化结构设计[6-8]等。由于每种硬件的特点不同,同一种模型结构在不同硬件上运行的效率也不同。 在边缘端推理加速算法研发时,需要针对不同芯片采用不同方案。多种方案叠加后,加速效果呈现非线性特点。 在对模型进行加速优化时,精确获得模型实际运行耗时是优化成功的前提条件。
现有的模型硬件耗时预测算法按发展的历程,主要可分为代理评估、硬件实测和算法预测3 类。
1) 代理评估。 采用容易获得的测评指标代替耗时指标。 早期深度学习模型主要应用在物体分类、识别等非实时任务上,在端侧部署的主要难点为参数存储。 Denton[9]、Han[10]等提出的算法以参数量为关注重点,将网络的存储压缩率作为评价指标。 随着深度学习在识别[11-12]与检测算法[13-16]的大规模应用,端侧模型的运行耗时成为主要优化目标。 介于当时的模型结构中操作类型少,卷积计算占比高[17-18],文献[19]开始将乘加运算次数(operations per second, OPS)作为主要评价指标,辅以理论内存进出消耗(memory access cost, MAC)辅助评价。 相对于以存储压缩率为指标,以乘加运算次数和内存进出消耗作为评价指标,能直接反映模型的理论算力和带宽需求。 由于不同芯片采用不同优化方式,理论计算结果与实际资源消耗存在差异。 部署时模型需反复试凑设计,对训练资源消耗大。
2) 硬件实测。 文献[20]在所提出的模型结构搜索算法MnasNet 中用了硬件实测方法,在优化算法执行中,将所得模型自动编译部署到实体硬件中进行耗时实测,并将测试结果向优化算法反馈。 硬件实测方法的优点是可以直接测量模型在特定硬件上的耗时,方法简单有效,但对部署系统设计能力及成本要求都较高。 此外实物系统受到系统调度等波动的影响,需要多次测试才能得到稳定的反馈,进一步增加了运行成本。
3) 算法预测。 通过构建数学模型,预测模型在实际硬件中的运行耗时。 Facebook AI 研究院在文献[21]中采用了查表法。 查表法通过板上实测手段对搜索空间中每种结构单元的耗时进行测量,构建[结构单元类型,耗时]的数据结构存表。 对于输入的待测模型,在进行结构拆解后,查询对应的结构单元耗时并累加后即得到预测耗时。 文献[22]中进一步对4 000 多种模型结构中的结构单元耗时进行采样,使用支持向量机(support vector machine, SVM)进行结构单元耗时预测建模,替代文献[21]中的数据结构表,一定程度上简化了所需资源。 文献[23]提出one-hot 编码方法,使得复杂网络结构可以简化为编码表,作为输入特征训练线性回归模型,直接对整体模型耗时进行回归。 文献[21-23]模型耗时预测算法,对于模块替换类结构搜索算法较为友好,但是受限于码表和传统回归算法的能力,在硬件编译器采用更加灵活的通道裁剪、混合量化、算子融合等精简手段时,优化空间复杂度指数级增长,预测误差较大。
本文提出了一种基于图卷积神经网络(graph convolution network,GCN)的卷积神经网络(convolutional neural network, CNN)模型推理硬件耗时预测新算法。 通过将卷积神经网络的拓扑结构转化为图网络,网络模型中各层的超参做为节点输入特征。 将网络模型在硬件上的前向推理过程当做黑箱系统,以耗时作为训练目标,通过学习网络结构间的关系,预测实际硬件耗时。 构建了基于MobileNetV2[7]的算法验证空间,在GPU、HISINNIE 硬核2 种硬件上验证了本文算法性能。 在模型自动裁剪、自动网络结构搜索等算法中,如需同时在精度和耗时等多方面达到最优,则可采用本文算法在多目标搜索优化过程中取代复杂的耗时实测过程。
1 图卷积网络
Kipf 和Welling[24]在2017 年提出了一种可扩展的图卷积神经网络。 图卷积神经网络融合了图神经网络和卷积神经网络的特点,将卷积神经网络从欧式空间扩展到了适合于表达关系网络的非欧空间,同时具有边与节点的可扩展性。
带有隐层的简单图卷积网络如图1 所示。 该网络由3 个层组成,分别为输入层、隐层和输出层,每层均含有Cx个通道,其中C1为输入通道,C2为隐层通道,C3为输出通道。 G 为图拓扑结构,该图为一个有4 个节点的无向图。 图1 中的虚线部分表示空域图卷积操作和非线性激活操作,其单层的前向传播如下:
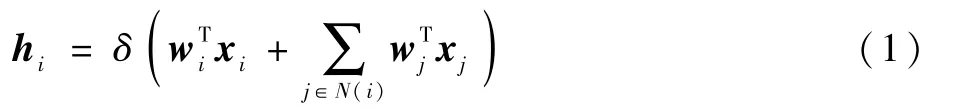
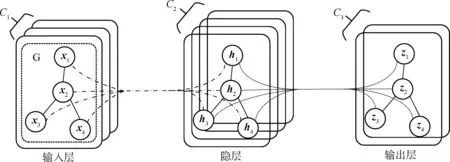
图1 带有隐层的图卷积网络示意图Fig.1 Schematic diagram of graph convolution network with hidden layers
式中:hi为隐层第i个节点特征值向量;wi为权重向量;xi为输入特征向量;N(i)为节点i的邻接节点集合;δ()为非线性激活函数。
为了能够与欧氏空间卷积相对应,可采用矩阵计算:
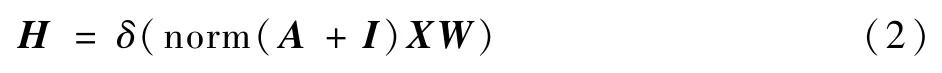
式中:A为邻接矩阵;I为单位对角矩阵;X为输入特征矩阵;W为权重矩阵;norm()为对矩阵的归一化。
用式(2)替代卷积神经元网络中的欧氏空间卷积操作,即可对图网络进行卷积计算。
如果将卷积神经网络结构作为输入特征数据,则预测器需要接受非欧空间数据,并对卷积神经网络结构中节点间拓扑关系具有较强的敏感度。 因此,本文选用图卷积网络对神经网络耗时进行建模预测。
2 基于图卷积网络的耗时预测算法
本节主要阐述基于图卷积网络的耗时预测算法核心设计,可分为卷积神经网络图编码、耗时预测算法整体设计与采样空间优化、图卷积网络设计与训练3 部分。
2.1 卷积神经网络的图编码
在利用图卷积对网络模型耗时预测之前,需要对卷积神经网络结构进行图编码。 编码分为2 步:
步骤1图网络中的节点用于表示卷积神经网络结构中的操作,边用于表示操作间的拓扑关系。 如图2(a)所示,现有主流卷积神经网络为有向无环图,拓扑结构可转换为图网络。 如图2 所示,根据边与节点的关系,可生成有向邻接矩阵A。具体的,由于图2(a)中共有4 个节点,为了表示节点间的连接关系,可以用一个维度为4 ×4 的邻接矩阵来表示。 如果第i行第j列的值为0,则表示第i个节点和第j个节点没有连接;如果为1,则表示存在连接。
步骤2节点特征矩阵用于表示网络中操作的属性超参集合,如图2(b)所示,特征矩阵F中第i行表示每i个节点操作具体的特征属性,m表示特征属性共有m维。 其中,节点的属性包括操作类型、卷积核尺寸、步进数、输入输出通道等。特别针对属性中的操作类型,使用one-hot 编码。如图2 (b) 中 的 操 作 种 类, “001” 表 示 卷 积(conv),“010”表示池化(Pool),“100”表示元素累加操作(EltAdd)等,其他特征则直接将值输入特征矩阵中。 当1 个节点操作不包含某个属性时,如元素累加操作(EltAdd)没有核大小和步进属性,则对应特征值设置为0。 经过上述的编码就可得到节点特征矩阵F。 在算法实际执行中,特征矩阵需要做归一化处理,避免不同尺度特征数据影响模型的训练收敛。

图2 网络结构和网络结构的矩阵Fig.2 Representation of a network and its matrix
2.2 耗时预测算法整体设计与采样空间优化
基于算法预测的耗时评测算法需要采集数据训练算法模型。 卷积神经网络的模型空间复杂度随着节点数与节点超参的增加成指数级增加,有限的训练样本无法表征空间的整体分布。 为了降低模型空间的复杂度,结合先验假设模型在实际硬件运行时,单个算子执行对耗时的影响仅与其邻近的节点距离为p以内的前置操作相关(p为常数),则整体网络的耗时可恒等变换成带有重叠拓扑结构的子网络差分累加:

式中:L()为网络在板上实测耗时;为整体网络N中第i个节点到第j个节点之间拓扑结构的子网络,i=j,表示单节点,i>j,表示空结构,空结构的耗时为0;n为整体网络包含的节点数, 即将整体网络耗时拆分为1 个子网络耗时L()与(n-p)个子网络对耗时差。 第i对子网络耗时差得到的是节点i的耗时补偿(L() -L())。
用图卷积去预测拆分得到的子网络集合,代入式(3)可以得到耗时预测模型:
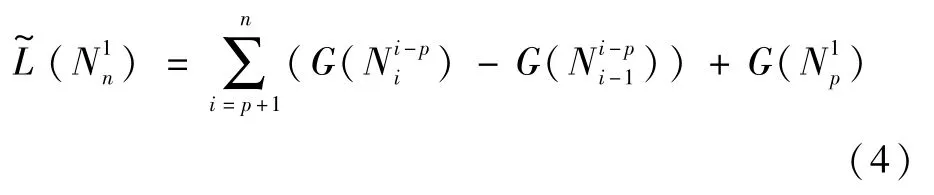
由于式(4)对应的所有子网络拓扑结构的最大节点距离均为p,故对预测模型G()进行训练的数据只需采集模型空间中最大节点距离为p的子结构集合即可。
通常无论是模型结构搜索还是模型裁剪,都面临结构空间复杂的问题。 假设模型空间为n节点单链结构,每个节点有m种可选特征属性(如操作类型、卷积核尺寸、通道数等),则整体模型空间的采样规模为mn。 而采用式(4)进行拆解后,子网络模型空间的采样规模则变为mp。 现有经典网络模型空间中n一般规模大于100,而硬件优化算法中对应的p一般小于10。 因此进行拆解可以大幅降低训练所需样本采样规模,模型空间复杂度的降低也使得图卷积网络的训练变得相对简单。 此外,利用拆解获得的子网络计算耗时补偿累加得到最终耗时预测的方式,能在训练过程中学习到编译器的算子融合技术对推理耗时的影响。
2.3 图卷积网络设计与训练
2.3.1 图卷积网络设计
本文采用GraphConv[25]中阐述的改进型图卷积神经网络,其单层前向的传播如下:
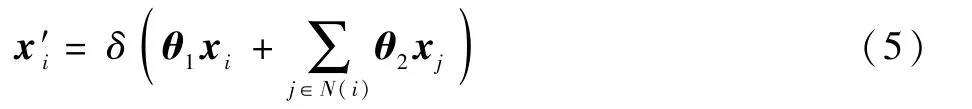
式中:xi为当前节点特征值;N(i)为邻接节点集合;θ为权重;δ()为非线性激活函数。
前向传播式(5)和图卷积神经网络的前向式(1)相比,所有邻边共享同一个权重θ2,模型参数量大幅减少,降低了过拟合的风险。 除此之外,为了缓解图卷积由于深度加深导致最后一层输出节点特征相似的固有问题,本文通过级联的方式融合浅层和深层的节点特征。
具体图卷积网路的结构如图3 所示,网络可分为3 个部分:输入、特征提取、累加输出。 输入部分将输入的卷积模型网络编码成邻接矩阵和特征矩阵。 特征提取部分由3 层GraphConv 结构级联而成,将浅层特征与深层特征进行拼接。 3 层图卷积层的节点输出维度分别是(100,100,1)。当输入节点的特征维度为m,则3 层图卷积输入的节点特征维度分别是(m,100 +m,200 +m)。最后一部分累加图卷积最后一层所有节点的1 维特征作为输出。
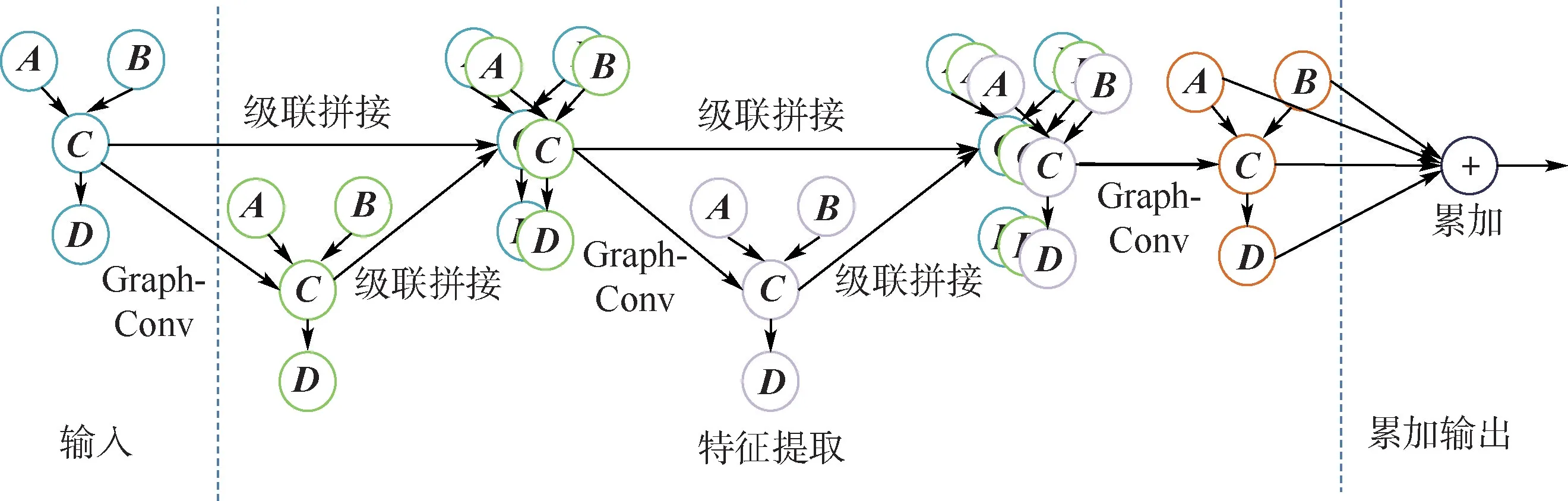
图3 图卷积网络结构示意图Fig.3 Structure of graph convolution network
2.3.2 图卷积的训练
图卷积的训练包括训练集采样与训练方案设计。
根据2.2 节所述,G()仅对拆解后的子模型空间中的结构进行耗时预测,故训练集为模型空间中最大节点距离p的子结构集合。 为了能在训练中获得式(3)中准确的单节点耗时补偿(L() -L()),本文设计了一种差分训练方案。 当采样获得了1 个子结构,则对应配置1 个附属子结构。 在训练中,不仅要训练G()对整体子结构的耗时预测能力,还要训练G()对单节点耗时补偿的预测能力。 故本文算法在训练时采用2 项损失函数:
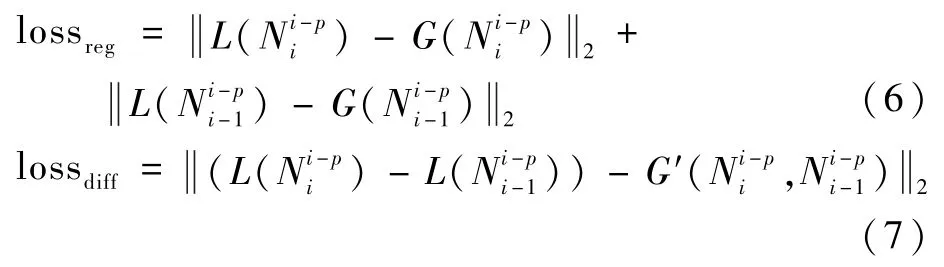

式中:G()和G()为图网络预测的子结构总体耗时;G′(,)为图网络预测的单节点补偿时间;α为[0,1]之间的实数,用来调整2 种损失函数之间的平衡;为二范数。
完整的训练方案如图4 所示。
对于每一组样本对,分别做如图4 所示的训练,训练G()对输入的图结构预测其整体耗时和最后一个节点的耗时补偿。 损失函数如式(6) ~式(8)所示。
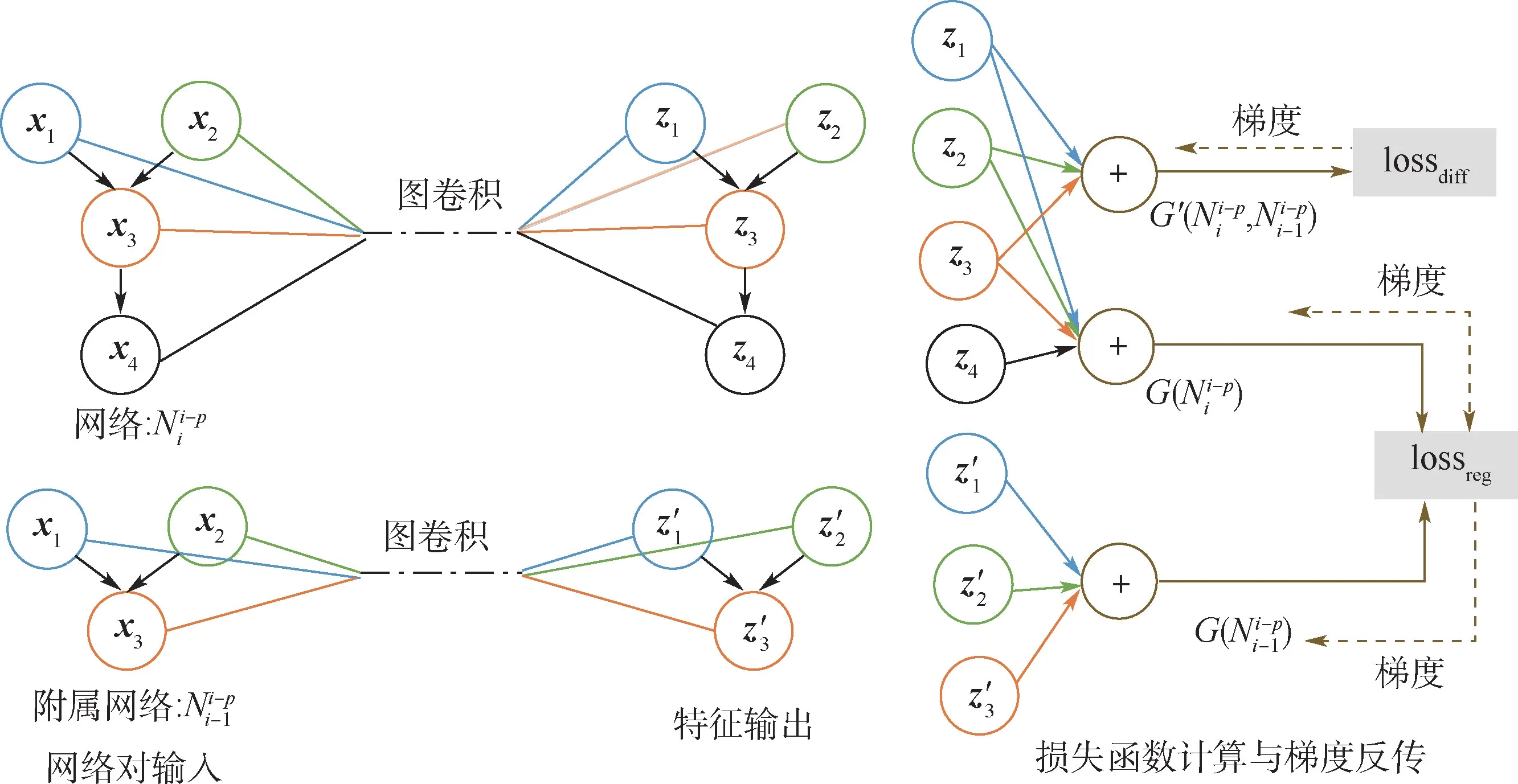
图4 图卷积训练示意图Fig.4 Schematic diagram of graph convolution network training
为了快速获得符合要求的训练集,本文使用的采样策略如下:在模型空间中随机采集大量完整网络;遍历完整网络中符合要求的子结构和附属子结构,测试2 个网络的实际硬件耗时,构成样本对;当遍历到某一节点时,以该节点为初始节点,向上包含所有路径长度小于p值的节点构成1 个子结构。
2.3.3 耗时预测推理过程
如图5 所示,本文算法对单个输入卷积模型进行耗时预测的完整推理过程。 主要可分为3 个步骤:
步骤1遍历每个节点进行网络划分,如图5中划分网络后得到网络1,网络2,…,网络N;网络划分的规则如下,对于当前节点i,向上包含所有路径长度小于等于式(3)中p+ 1 值的节点。图5 是p=1 的情况,可以看到,节点i-1 和节点i得到的子网络就是在整体网络中以当前节点为初始节点向上截取了路径长度小于等于2 的所有节点构成的网络。
步骤2对划分得到的子网络进行编码,得到邻接矩阵A和特征矩阵F,进行相应图卷积计算,得到子结构总体耗时和单节点补偿时间的预测;除第一次的子网络会将子结构总体耗时预测输出到累加器之外,其他的子网络均只将当前节点的补偿时间预测输出到累加器。 如图5 所示,假设当前节点为i-1 节点,输出到累加器的是当前节点补偿时间ti-1即为z4特征。 当前节点变为i节点时,输出到累加器的是第i节点补偿时间ti即为z5特征。
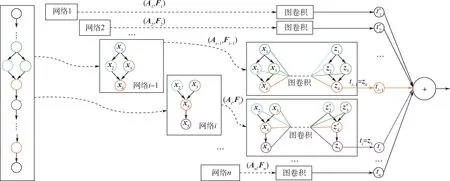
图5 耗时预测前向示意图Fig.5 Procedures of latency prediction
步骤3累加以上预测值得到网络的整体耗时。 需要说明的是,不同于之前的单节点耗时相加的算法,本文所提算法输入的是1 个网络,输出的是节点耗时再进行累加,并包含了补偿信息,故可认为是一种整体法,能得到更加精确的整体耗时预测。
3 实验结果与分析
3.1 实验平台
本文实验选取海思端侧硬件平台和英伟达GPU 平台进行验证。 HISI3559 平台是海思一款边缘端数字信号处理芯片,带有深度学习硬核。该硬核在编译使用时对网络推理有一定的自动优化。 本文实验中HISI3559 的编译器版本为2.3.5。GPU 平台具体型号为TeslaV100-SXM2-32GB。 针对神经网络推理,英伟达公司开发了一套加速工具TensorRT,本文实验中的GPU 部署使用词工具对网络推理进行优化加速。
由于测量耗时存在一定理论波动,本文实验每个真值采用10 次测试取平均值得到。
3.2 输入空间与训练集
为了验证耗时预测算法在不同输入空间的有效性,实验分别在离散空间(mobilenet block,MB)和连续空间(mobilenet block-continuous, MBC)进行实验。 离散空间和连续空间的区别在于空间中是否含有如通道数比例这种连续的变化属性。 MB 提出于文献[19],借鉴了MobileNetV2 的结构,空间由16 个可进行类型选择的层组成,且其被分成4 个阶段,单个阶段内,每层的输入输出分辨率相同,阶段间由下采样层连接,将分辨率降为原来的一半。 具体结构如图6 所示。 图6 中输入的图像高为H,宽为W,输入通道数为Cin。 经过1 ×1的卷积,将通道数变为原来的e倍,e的取值范围为{3,6}。 可分离卷积的卷积核尺寸大小可选范围为{3,5,7}。 最后经过1 ×1 卷积将输出通道数变为Cout。 非下采样层还会带有短接操作。 每层之间可以独立选择短接操作来控制网络深度。 MB-C 则是在MB 基础上加入连续通道数的变化。 通道的可变化比例为[0.35,1],每组通道数的选择范围是{1,8,16,32}。
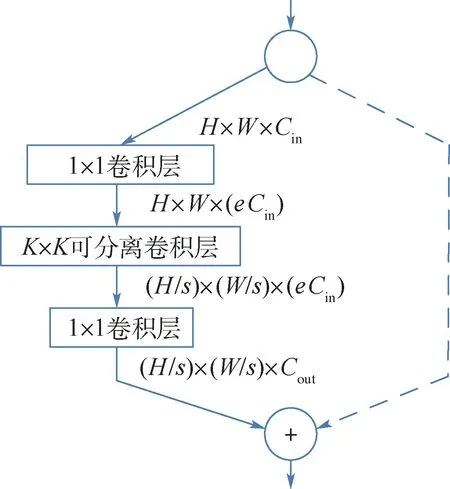
图6 MB 空间层选项示意图Fig.6 Candidate operations of layers in MB space
对于耗时模型训练所需要的数据集,先在2 个空间上各自随机采样100 个独立模型,之后根据2.3.2 节中所述算法采样双网络训练集。 测试集为2 个空间中各随机采样1 000 个模型构成。
3.3 模型训练与评估
图卷积网络训练参数如下,设置式(4)中p参数为2,训练时使用Adam 优化器。 权重初始学习率为0.01,单批次数据量为128。 总共训练迭代1 000 轮。 每100 轮学习率下降为之前的30%。 为了多维度证明算法的有效性,实验设置了多个评价指标,包括平均相对误差(MRE)、最大相对误差(MAX)、5%误差样本占比、10%误差样本占比。 各个指标具体介绍如下:
MRE 指标为测试集样本预测相对误差的平均值,其计算式为
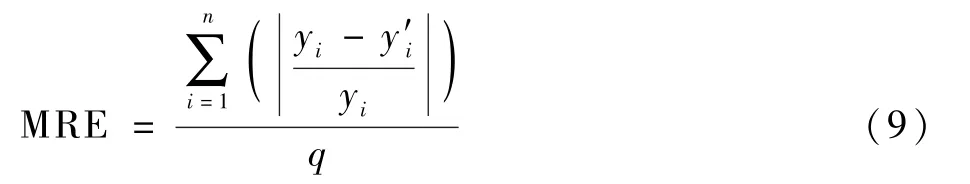
式中:yi为模型的真实耗时;为算法预测耗时;q为测试集样本数。
MAX 指标为测试集中预测的最大相对误差,其计算式为
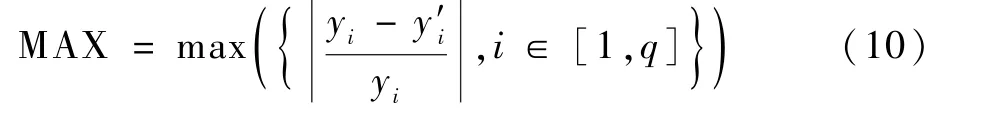
5%误差样本占比为测试集中预测相对误差在5%以内的样本数占总样本数的比例;10% 误差样本占比为模型预测相对误差在10% 以内的样本占总测量样本的比例。
3.4 针对离散空间的耗时预测算法对比
本节实验针对MB 空间,将本文算法和传统算法进行对比。 对比算法包括单层预测累加、查表累加和基于one-hot 编码的系列算法。 其中,基于one-hot 编码的系列算法具体包括SVM回归(线性核、高斯核)、贝叶斯回归、拉索回归和随机森林回归。 各算法的性能测试结果如表1所示。
本文算法(图卷积网络)在HISI3559 上的平均相对平均误差为0. 5%,最大相对误差为2.4%。 2 种指标均超越了其他算法。 在GPU 平台上,本文算法的最大相对误差为10.0%,优于其他算法,而平均相对误差除比拉索回归(2.8%)略低0.3%外同样优于其他算法。 表1 证明了基于图卷积网络的耗时预测算法在不同硬件平台上可以有效建模。 从本文算法和单层预测累加算法对比中可以看出,本文算法性能的提升来自于图卷积的建模能力和耗时补偿机制的提出。

表1 离散空间耗时算法对比Table 1 Performance comparison of algorithms in discrete search space
从表1 中进一步发现,相比GPU 平台,本文算法在HISI3559 平台的精度提升更加明显,其原因可能是HISI3559 的层间融合策略多于GPU。由于本文算法中耗时补偿的建模机制可以有效估计层间融合对耗时的影响,最终导致HISI3559 平台上的预测精度提升比GPU 平台更为显著。
3.5 针对连续空间的耗时预测算法对比
本节实验针对MB-C 连续空间,将本文算法和传统算法进行对比。 对比算法是单层预测累加算法。 需要说明的是,由于连续变量无法使用one-hot 编码, 基于one-hot 编码的相关算法无法应用于连续空间。 另外,由于连续空间提取查表的空间过大,查表累加算法也不适用。 因此,本节实验与单层预测累加算法进行对比。 2 种算法在不同平台上的性能如表2 所示。
从表2 可得,本文算法在HISI3559 平台上5%误差样本占比和10% 误差样本占比分别为63.8%和99.7%,性能远超单层预测累加算法的0%(所有测试样本误差均大于10%);对于MRE和MAX 指标,本文算法相比单层预测累加算法的误差也降低了至少1 个数量级。 在GPU 平台上,本文算法的性能相对单层预测耗时累加算法也有显著提高。 本节实验现象表明,在HISI3559和GPU 平台上,本文算法由于图编码的有效性和图卷积高效的建模能力,使其仍可以针对连续空间进行有效建模,并且性能远超单层预测累加的算法。
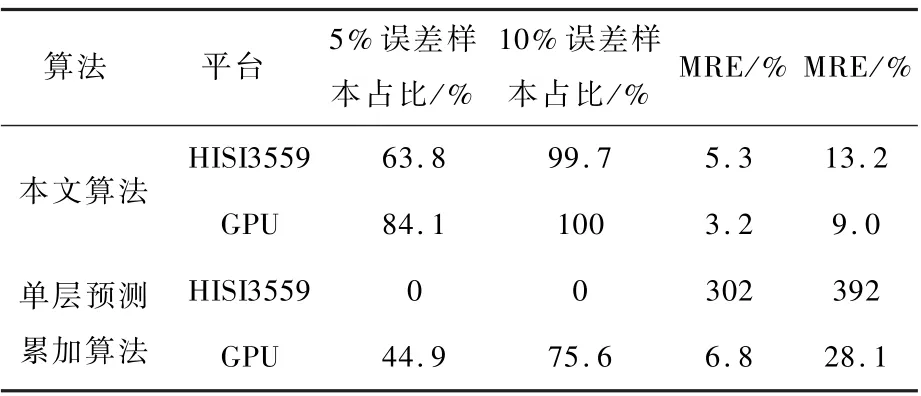
表2 连续空间耗时算法对比Table 2 Performance comparison of algorithms in continuous search space
3.6 p 参数假设的有效性讨论
本文算法基于式(3)中的假设:单个算子执行对耗时的影响仅与其邻近的节点距离p以内的前置操作相关(p为常数)。 本节以实验来讨论此假设的有效性。
选择目前主流网络MobileNetV2、IncptionV2、ResNet50。 将不同的p值代入式(3)获得的预测耗时与真实耗时进行比较。 实验结果如图7所示。
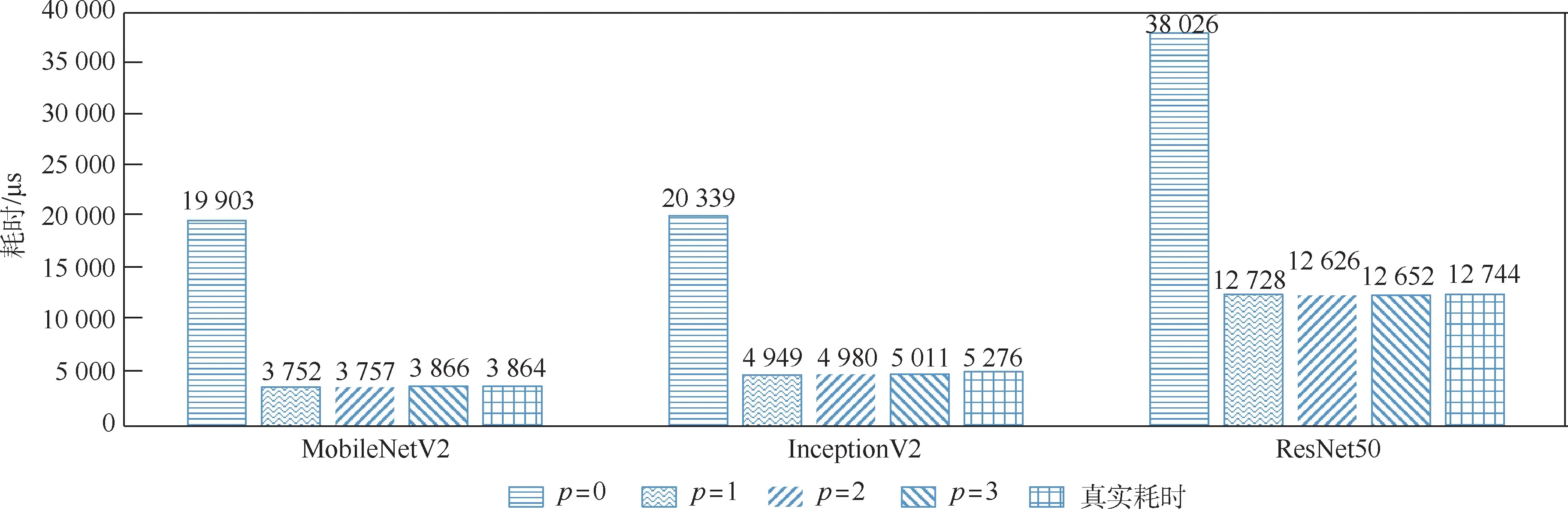
图7 不同p 值得到的耗时与真值对比Fig.7 Comparison of latency with different p values and real latency
图7 共包含3 组直方图,分别表示3 个不同的网络。 每组直方图都存在5 个纹理不同的柱形数据,柱状图高度表示相应设置获得的耗时。p=0 指单层测量直接累加所得值。 从图7 中可得,p=0的耗时累加值和真实耗时差异巨大,说明HISI3559芯片运行时存在层间融合优化,使得整体耗时与单层耗时单纯累加差异甚远。 但当p=1时,其耗时累加值和真实耗时的差异就大幅降低。 当p≥1 时,这种差异仍然有所降低,但边际效益已不高。 这说明HISI3559 平台绝大多数的单个算子执行对耗时的影响仅与其邻近的节点距离为1 以内的前置操作相关。 基于本节实验现象,说明当p≥1 时,式(3)中的假设在HISI3559 平台上是成立的,考虑到输入空间规模和耗时预测精度的权衡,在本文实验中,p设置为2。
3.7 结合图卷积网络耗时预测的网络结构搜索
将本文算法应用到多目标(精度与耗时)网络结构搜索中。 实验使用MB-C 连续空间,搜索任务针对ImageNet100K 数据集的分类任务,将搜索目标耗时设置为4 ms。 具体网络结构搜索算法为:第1 步,借鉴文献[26]训练超级网络来快速评估每条支路的精度;第2 步,根据文献[27]提出的遗传算法搜索耗时接近4 ms,且性能尽量高的模型。 对比实验设置为:在其他实验条件保持相同的情况下,一个使用单层预测累加的耗时预测算法,另一个使用基于图卷积网络的耗时预测算法,对比搜索出来的网络性能。 具体的实验结果如表3 所示(硬件平台为HISI3559)。
从表3 可得,在保证其他搜索设置相同的情况下,使用单层预测累加算法搜索到的网络耗时为4 256 μs。 使用本文提出的耗时预测算法搜索到的网路耗时为4 055 μs。 本文算法更接近预设的目标耗时(4 000 μs),精度也没有损失。
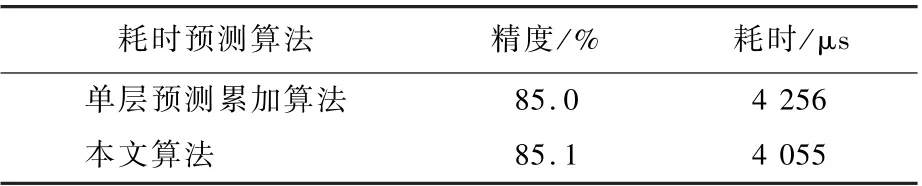
表3 耗时预测算法对结构搜索的作用Table 3 Effect of latency predictor on neural architecture search
4 结 论
传统的耗时估计算法无法很好地同时解决硬核加速器层间融合优化的建模问题和输入空间过大导致的采样成本高的问题,为此本文提出了一种基于图卷积的耗时预测算法。 主要改进如下:
1) 将网络模型编码成有向无环图,提出了基于图论的网络结构编码算法。
2) 将整体耗时模型恒等拆分成子网络对,并提出了有效的近似假设,减少了输入空间规模,降低欠拟合风险。
3) 设计了完整的图卷积网络结构,使用了浅层和深层特征融合的技术提高网络的建模能力。
4) 设计新的损失函数,有效训练图卷积回归模型。
5) 在不同网络空间和硬件平台上证明了本文算法的有效性,针对HISI3559 平台,本文算法在MRE、MAX、5% 误差样本占比、10% 误差样本占比4 项指标均超过现有耗时估计算法,特别在MB-C 连续空间上,针对HISI3559 平台,本文算法将MRE 从302%降低到5.3%。
6) 将本文算法与模型结构搜索算法结合,在特定硬件上搜索到既高效又高精度的模型。
本文算法能够与结构搜索、通道裁剪、量化等多种优化手段结合,对边缘侧部署模型优化有重要意义。
