一种方形腔体的目标散射特性及测量方法

赵京城, 娄长玉, 李家碧, 杨宗凯

(北京航空航天大学 电子信息工程学院, 北京 100191)

雷达散射截面(radar cross section,RCS)是武器系统隐身性能的重要指标[1],是定量表征目标散射强弱的物理量[2],通过研究目标的散射特性,运用材料及外型技术,减少目标的RCS 值,在隐身技术领域有重大意义。

理论分析和实验结果都已证明,发动机进气道对飞机和导弹的雷达散射截面有重要的影响[3]。 因此,在计算现代飞行器的RCS 值及进行隐身外形设计时,应充分考虑进气道结构的电磁散射特性[4]。 鉴于进气道的几何形状和结构复杂,通常将进气道简化为腔体模型来研究其散射特性[5]。

国内外已经开展了腔体电磁散射方面的研究,发展形成了一套系统的、科学的研究方法。 除了传统的解析方法、时域的积分方程解法、频域的矩量法、有限元法等数值计算方法[6]外,还有几何 光 学 法[7-9]、 物 理 光 学 法[10-12]、 射 线 追 踪法[13-14]、广义射线法[15]、复射线法[16]等高频近似方法。 矩量法等精确数值计算方法只能求解电尺寸较小的散射体[17],而高频近似解法具有物理概念清楚、场分布可以直接写出表达式和方法简单易用等优点。 在测量方面,一般测试场仍将进气道作为普通目标看待,按照三维最大尺寸(通常是长度)计算远场条件和设置距离门参数。 但是,按照波导理论分析,腔体散射应该只与口面场相关,远场条件也应该按照口面尺寸计算。 另外,由于腔体存在多次反射,反射路径远大于腔体长度,因此,距离门参数按长度设置可能给测量带来较大误差,本文将在腔体目标的远场条件分析和多次散射距离两方面进行深入研究。

本文根据矩形波导理论分析腔体散射只与口面场分布相关的机理,用几何光学法推导腔体模型的散射距离与电磁波入射角度即方位角的关系。 用FEKO软件对腔体模型进行散射场计算,验证理论推导的正确性。 将腔体实物模型分别置于紧缩场和普通远场暗室中测量,验证腔体散射只与口面场有关。 同时设置不同的距离门参数,验证腔体类目标测量系统需要具备的距离测量能力。

1 腔体目标散射机理

1.1 矩形波导理论

根据矩形波导传输特性,电磁波在金属腔体内传输可视为波在波导内壁间连续入射与反射[18],构成导行波沿波导传播。

对于闭合金属腔体而言,外加电场不影响腔体内部电场[19],对于进气道来说,与闭合腔体不同的是一端开口,入射电磁波通过口面进入腔体内部,散射电磁波通过口面传播到腔体外部,腔体外表面的电磁场不影响腔体内部散射。

在测量进气道等腔体类目标的RCS 时,由于腔体内部电磁场与腔体产生的散射场均由进气道口面场决定,与进气道外壁电磁场分布无关。 因此,在计算远场条件时,不需取目标三维最大尺寸(如进气道长度),只需取口面最大尺寸即可。

1.2 传统目标RCS 测量方法及要求

RCS 测量要求用平面波照射,但是实际天线发射的是球面波,将一个已知特性的发射天线设置在远处向待测天线照射,当发射天线的波前阵面扩展到一定程度,可认为待测天线接收的是近似平面波的照射,满足近似条件的距离称为远场条件,其示意图如图1 所示。

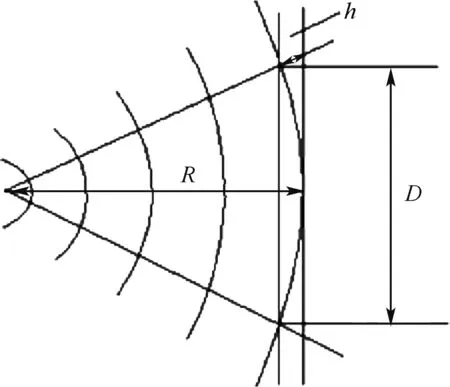
图1 远场条件示意图Fig.1 Schematic diagram of far field conditions

目标口面尺寸D的相位差满足:

其中,k=2π/λ,为保证一定的测试精度,要求相位差Δφ≤π/8 =22.5°,此时满足D≪2R的条件,有

此时雷达与被测目标之间的距离R满足:

式中:D为目标口径;λ为波长;2D2/λ为实际测量中最小的测试距离。

引入远场条件的基本出发点是要求在被测目标口径平面上的相位变化小于π/8。 在计算远场条件时,一般取目标三维尺寸中最大的一维。 对进气道来说,其长度往往比口面尺寸大,因此,需要使用长度计算远场条件。 由此计算得到的测量距离一般较大,需要在大型测试场中进行测量,成本较高。 但是,进气道等腔体类目标散射机理与一般凸表面目标不同,有2 个问题值得深入研究:①远场条件是否应该按照长度计算;②按照长度计算出的远场条件下是否能获得准确的测量结果。

1.3 腔体类目标散射特点

腔体散射最主要的特点是在腔体内部产生的多次反射,此外,在腔体边缘产生的绕射也会对腔体散射产生一定影响。

1.3.1 多次反射

电磁波照射到腔体口面后,会在口面处形成口面场并进入到腔体内部如图2 所示,在腔体内壁之间经过多次反射后,能量会从腔体口面处再次辐射到远区,多次反射对腔体散射起到十分重要的作用。

L为腔体模型长度尺寸,D为腔体模型口面尺寸,θ为电磁波(以下用射线代替)入射方向与腔体模型轴向夹角,红色标记处为射线1 的反射位置。 记射线1 在目标模型轴向的投影为d(见图2)。 下面采用几何光学法详细地分析腔体内部的单站回波特性,其中,m1=2L/d且2L可被d整除,如图3 所示。

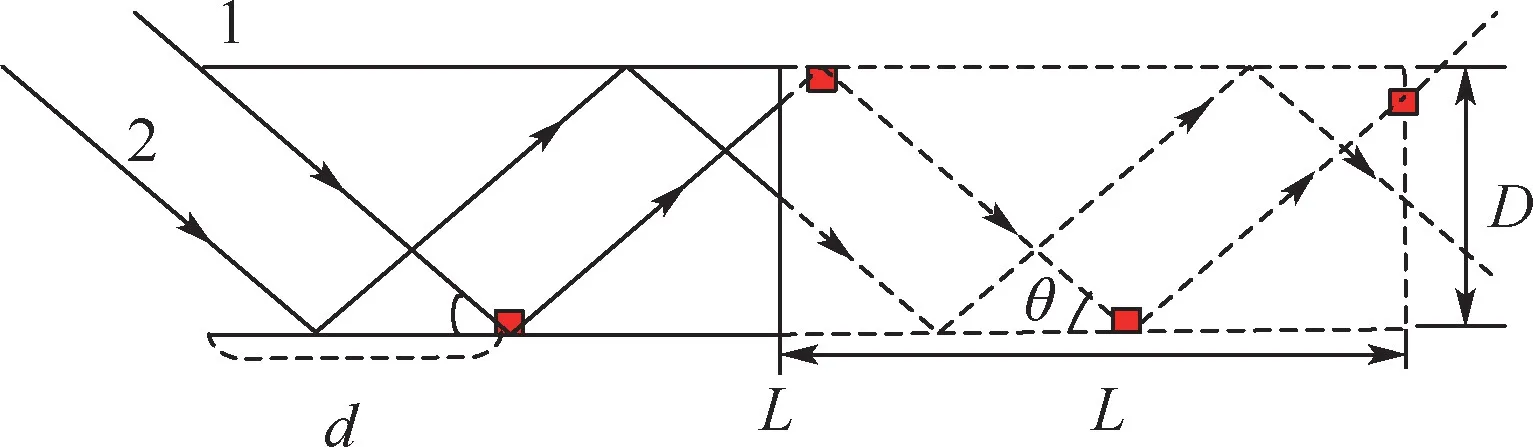
图2 腔体内壁多次反射示意图Fig.2 Multiple reflection of cavity inner wall

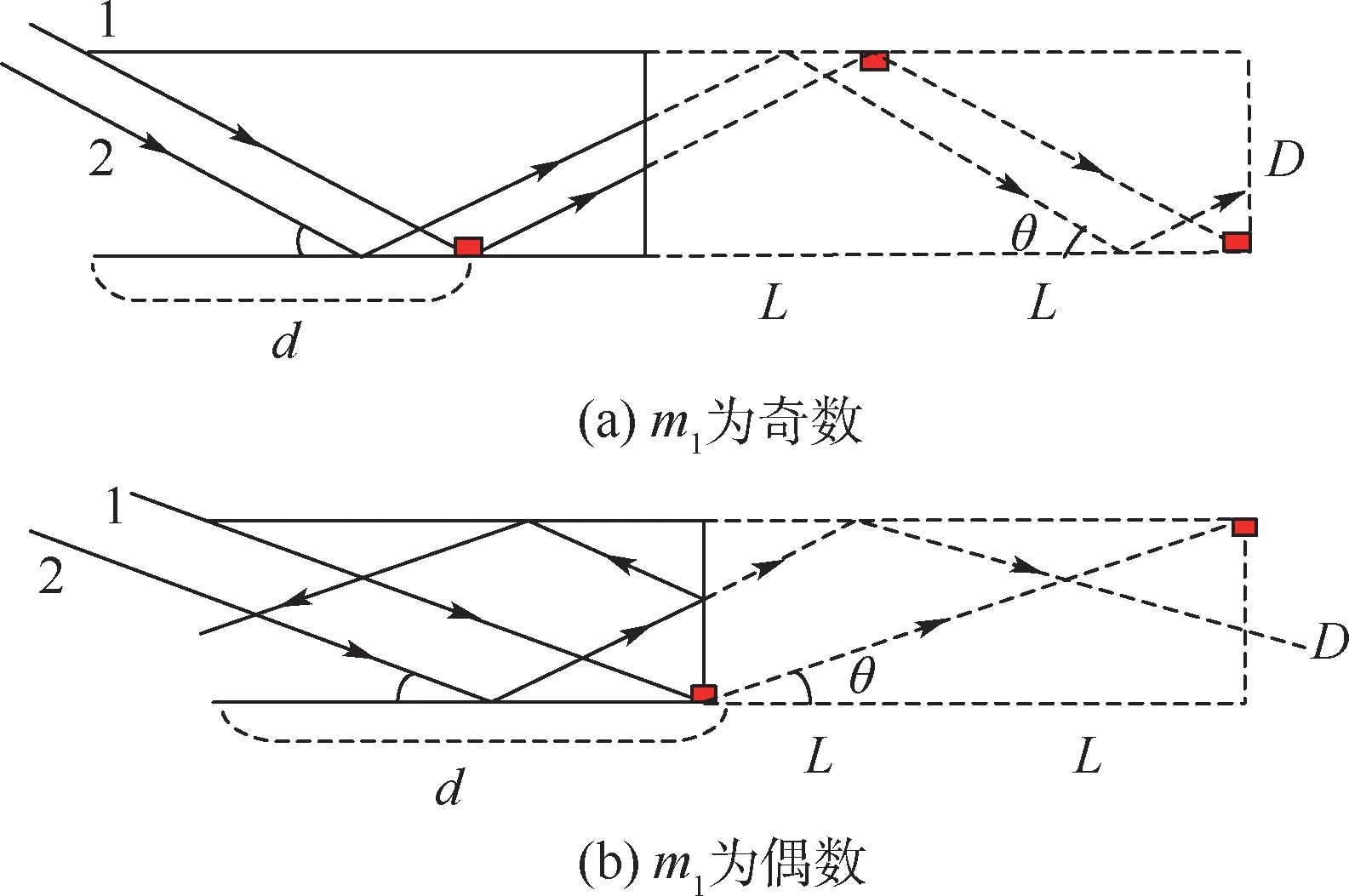
图3 腔体部分回波示意图Fig.3 Echo diagram of cavity part

本节分2 种情况予以说明。

1) 临界角度情况(2L可以被d整除)。 依据几何光学原理,射线在腔体底面反射,相当于以底面为对称轴做镜像。 因此,可以做腔体镜像来分析。 若回波方向朝上,表示回波沿入射方向返回,即接收机可以接收到回波功率的单站情况;若回波方向朝下,表示入射方向没有回波,即接收机不能接收到回波功率。 可用回波比例来表示腔体多次反射后单站接收的回波情况。

①若m1=2L/d为奇数,如图3(a)所示。 朝向目标的箭头代表电磁波入射方向,另一个代表水平极化。 不难发现除了射线1 以外,其余射线的出射方向均朝上,即全部的射线沿入射方向返回;其回波方向可用如图4(a)所示的情况来呈现。 该图是在FEKO 软件中对口面尺寸D=0.11 m、径向长度L=0.3 m 的方形腔体,在方位角为10.39°时计算获得的水平极化双站散射方向图,频率为15 GHz。 此时回波比例为1。

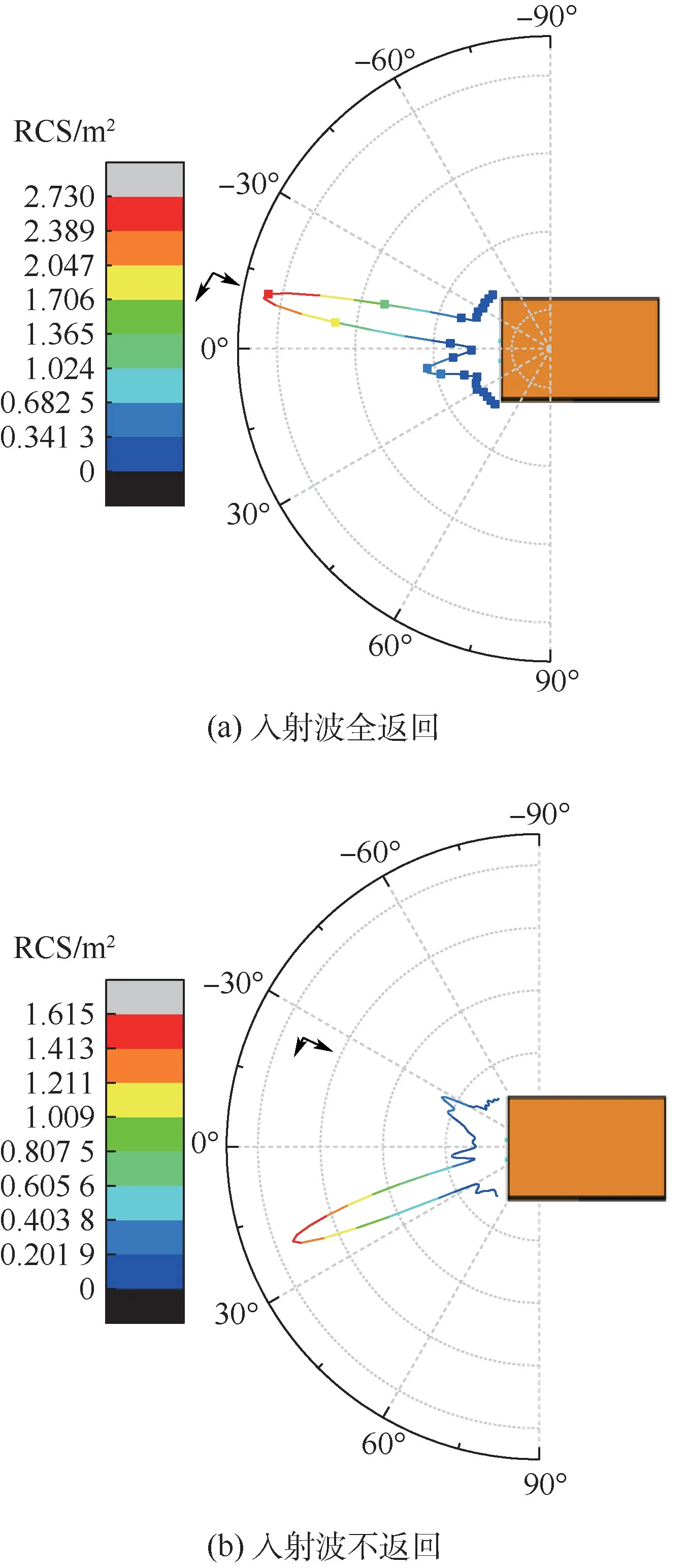
图4 入射临界角返回情况Fig.4 Return of critical angle of incidence

②若m1=2L/d为偶数,如图3(b)所示。 亦不难发现除了射线1 以外,其余射线出射方向均朝下,即入射方向没有回波,其回波大致方向如图4(b)所示,方位角为20.2°。 此时回波比例为0。

2) 一般角度情况(2L不可被d整除)。 实际入射方向与模型轴向夹角即方位角θ从0° ～90°变化。 除了某些角度下2L可以被d整除,其余角度2L均不能被d整除。

①若m2=2L/d为奇数,记d1=2L-m2d为d整除2L后的剩余长度。 如图3(a)所示,此时射线1 在镜像底面上是朝上射出的,存在一条射线,其下的所有射线均朝下射出。 这个临界射线在入射口面处距离射向内壁的垂直距离为d1tanθ,因此回波比例p为

②若m2=2L/d为偶数,记d1=2L-m2d为d整除2L后的剩余长度。 如图3(b)所示,此时射线1 在镜像底面上是朝下射出的,存在一条射线,其下的所有射线均朝上射出。 这个临界射线在入射口面处距离射向内壁的垂直距离也为d1tanθ,因此回波比例p为

式中:d=D/tanθ,m2= 2L/d= 2Ltanθ/D,得到d1=2L-m2d。 其回波方向如图5 所示,方位角为34°。

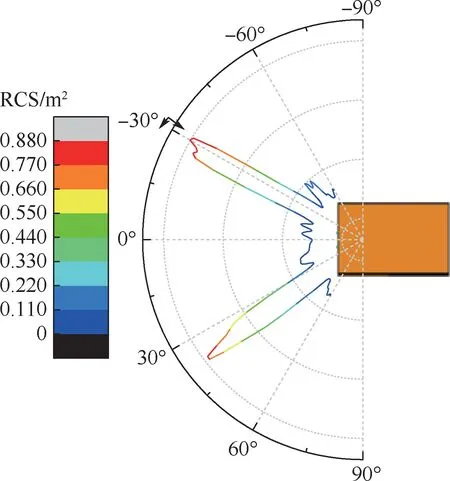
图5 入射波返回的一般情况Fig.5 Return of incident wave

显然,方形腔体多次反射情况与平面波方位角关系密切,随着角度变化,入射到腔体口面处的能量按余弦规律减小,方形腔体的归一化回波比例为

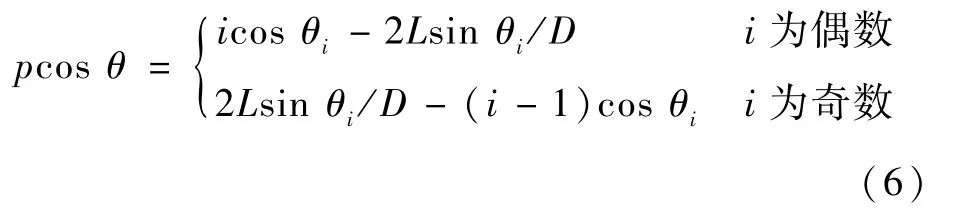
式中:i为偶数时,对应图4(a)中入射波全返回的情况;i为奇数时,对应图4(b)中入射波不返回的情况。

当方位角为小角度时,投影部分远大于2L,0°正入射时入射波全返回,角度偏离0°能量会立即减小至0,小角度时能够单站返回的部分投影为2L,即p=2L/d=2Ltanθ/D,小角度范围内的归一化回波比例为

同时,随着方位角的变化,散射距离s也会随之变化,s=L/cosθ,相对于腔体径向长度,其散射距离倍数为

本节所述,可得到方腔单站归一化回波比例曲线与腔体径向长度倍数曲线。 通过FEKO 软件仿真计算来验证推导结果,并对推导结果和仿真计算结果做归一化处理。 图6 为口面尺寸D=0.11 m、径向长度L=0.3 m 的方形腔体在不同极化状态下的推导结果与不同频率下FEKO 单站仿真计算曲线。

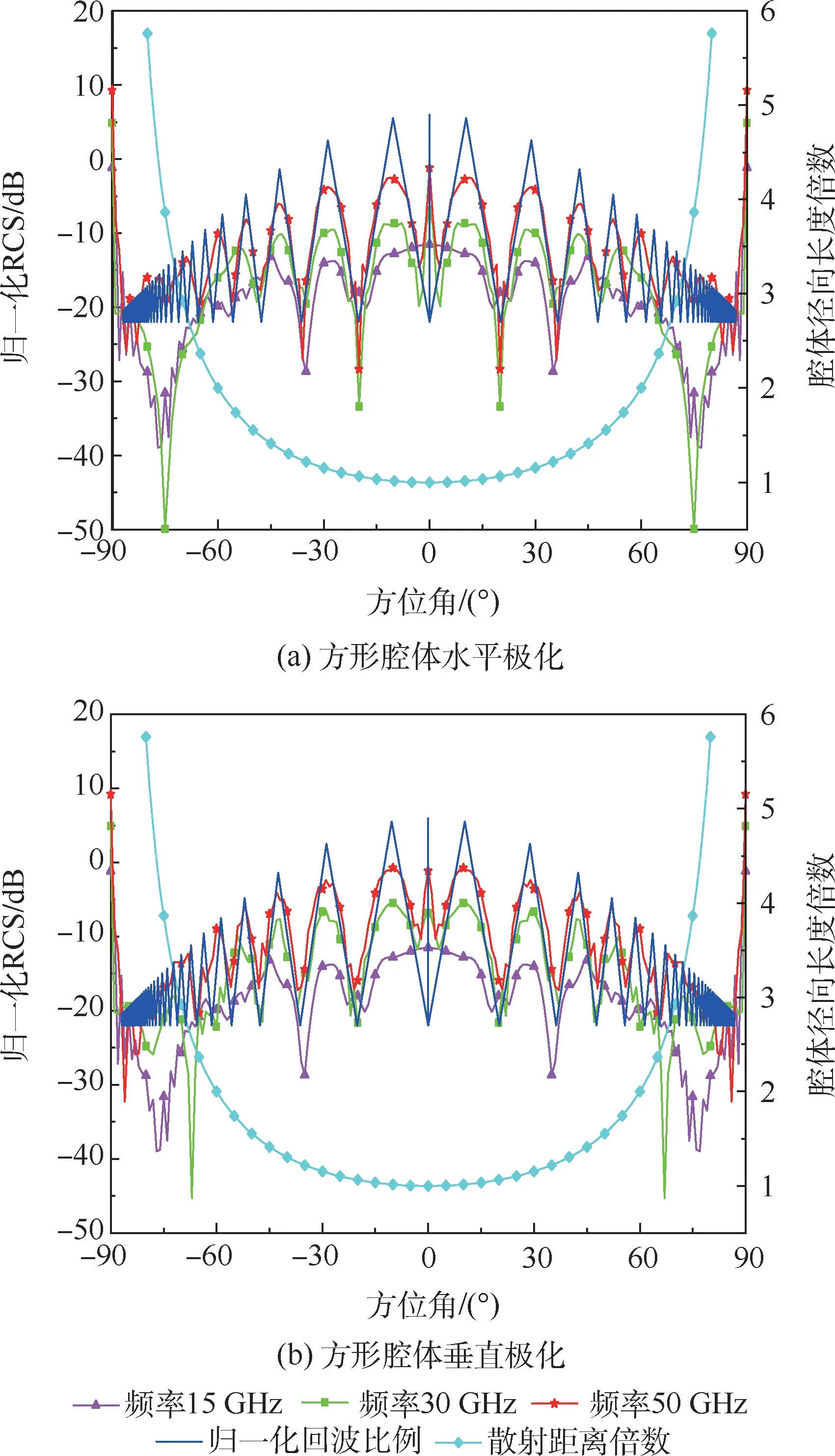
图6 不同极化状态下推导结果与FEKO 仿真计算的归一化曲线Fig.6 Normalized curves between derived results and FEKO simulation results under different polarization states

由图6 可知,归一化回波比例曲线与不同频率下FEKO 单站仿真计算曲线趋势相同,方位角从0° ～90°,其归一化RCS 都有降低趋势,并且两者的尖峰与低谷位置一致。 由于理论推导采用的是几何光学法, 频率更高的50 GHz 比30 GHz的曲线更接近于理论推导结果。 此外,散射距离会随方位角增加而增加,并且增加的斜率逐渐变大。

1.3.2 边缘绕射

电磁波在经过飞机进气道的棱边、缝隙等障碍物时,不能被直接照射到阴影区域内,而是会偏离直线传播进入该区域,即产生绕射。 阴影区的绕射场也会对腔体的散射起到一定作用。

2 仿真计算及成像分析

2.1 仿真建模计算

计算模型与1.3.1 节中验证理论推导的模型相同,口面尺寸D为0.11 m,径向长度L为0.3 m。

平面波入射方向与腔体轴线在同一个平面上,方位角范围为-90° ～90°, 如图7 所示。 角度间隔为1°,计算频率为15 GHz。 由图8 仿真计算结果看出:方位角在60° ～90°范围内,金属腔体的外壁散射较大,影响对腔体散射的分析。 为了更好地研究腔体内部多次反射特性,应减小外壁的散射值。 在腔体内外表面分别涂覆2 种吸波材料,其中吸波材料1 的电磁参数为介电常数实部εr=4,介电常数虚部εi=1.2,磁导率实部μr=1.2,磁导率虚部μi=0.6,涂在内壁。 吸波材料2的电磁参数为:介电常数实部εr=1,介电常数虚部εi=0.6,磁导率实部μr=1.2,磁导率虚部μi=0.6,涂在外壁。 通过FEKO 仿真计算2 种吸波材料的反射率,如图9 所示,吸波材料1 的反射率在-10 dB 左右,吸波材料2 的反射率在-30 dB 左右。 方形金属腔体和内外壁涂有吸波材料腔体的RCS 对比曲线如图8 所示。

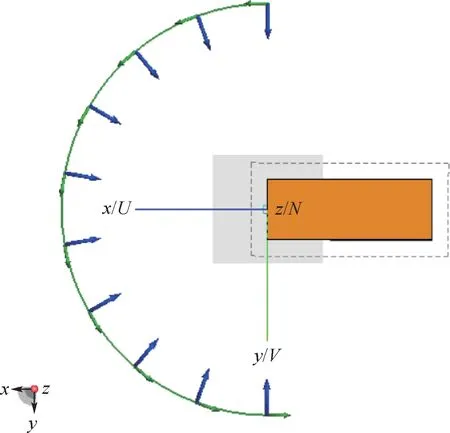
图7 方位角示意图Fig.7 Schematic diagram of azimuth angle

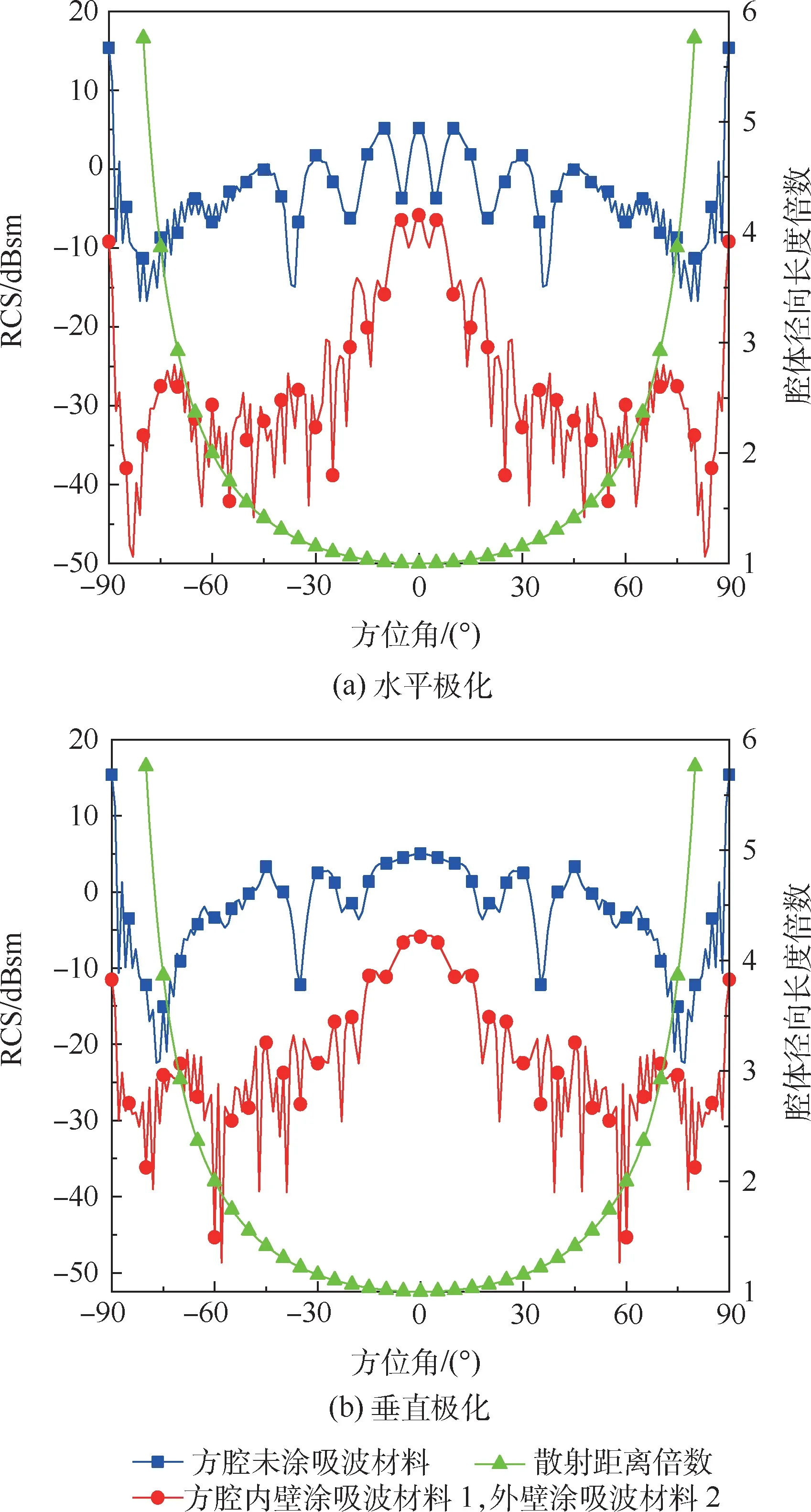
图8 15 GHz 不同极化状态下金属腔体与涂吸波材料腔体的RCS 曲线对比Fig.8 RCS curve comparison of metal cavity and cavity coated with absorbing material under different polarization conditions at 15 GHz

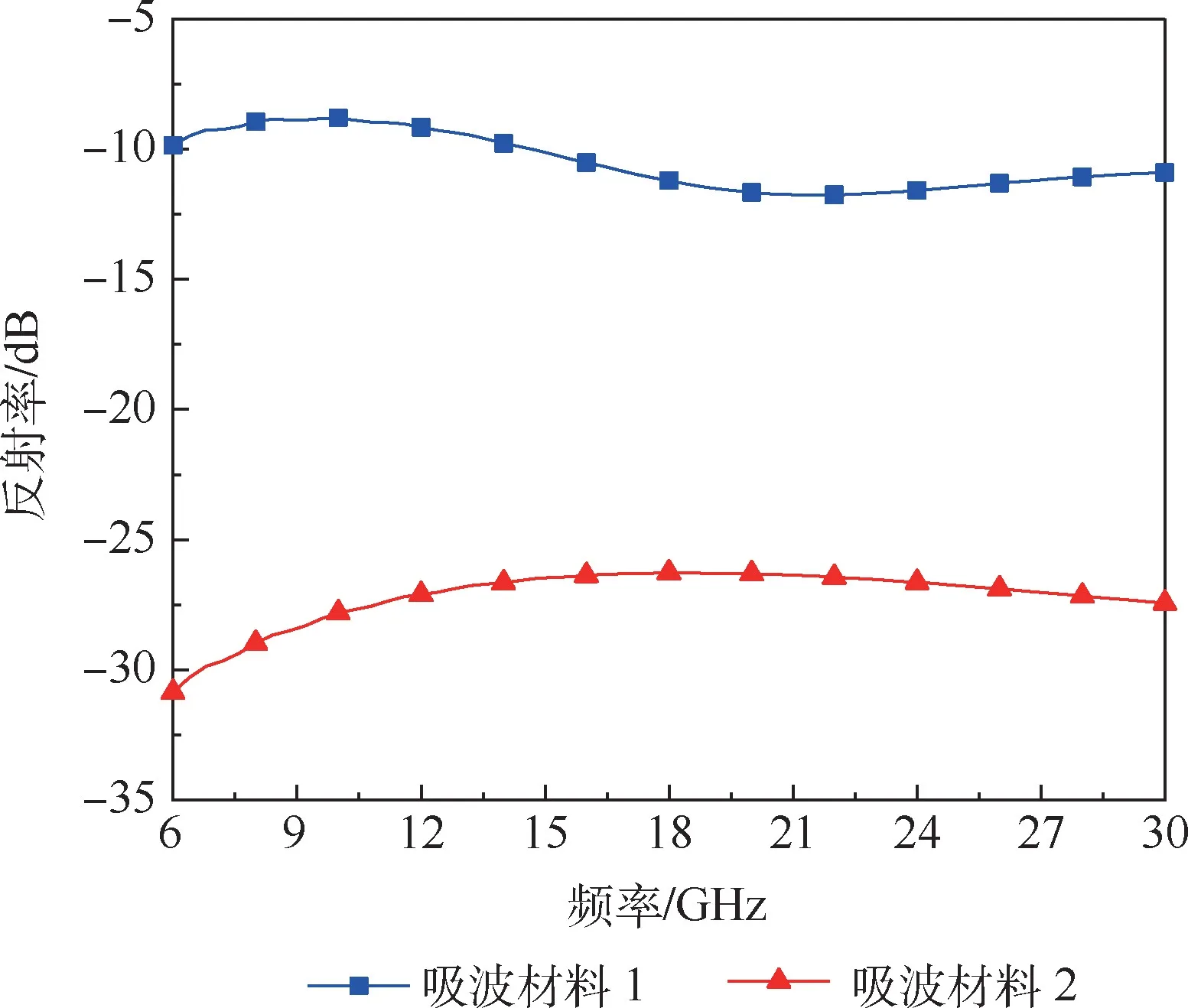
图9 两种吸波材料的反射率特性Fig.9 Reflectivity characteristics of two absorbing materials

由图8 可知,方位角在30°～60°( -60°～-30°)范围内,涂有吸波材料腔体的RCS 相比于金属腔体的RCS 显著减小,这与该方位角范围内腔体多次反射特性一致;从2 种RCS 曲线可以看出,方位角在±60°附近出现拐点,这是因为方位角在0° ～60°( -60° ～0°)范围内,腔体内部反射为腔体散射的主要部分;方位角在60° ～90°( -90° ～-60°)范围内,腔体外壁散射影响逐渐变大。 结合测试距离倍数曲线可以看出,当腔体内壁使用吸波材料时,随着方位角变大,散射次数增加,散射幅度随角度衰减较快。 在吸波材料性能较好的情况下,散射测量系统具备2 ～5 倍腔体径向长度的测量能力即可准确测量腔体散射。

2.2 一维距离像验证

图8 中的散射距离曲线是通过理论计算得出,可采用一维距离像来验证。 选择一维像计算角度为0°、43°、59°、75°,这些角度分别对应于腔体散射角度曲线中的峰值角度。 选择水平极化方式,计算频率范围为13 ～17 GHz,得到不同方位角的一维距离像如图10 所示。

由图10 可知,随着方位角增大,一维像的尖峰逐渐右移,即腔体内部散射的成像距离逐渐变大;方位角为0°、43°、59°、75°时理论计算的成像距离分别为0. 3 m(1 倍)、0. 41 m(1. 367 倍)、0.58 m(1.94 倍)、1.16 m(3.86 倍),图10 中腔体内部多次反射的成像位置与理论距离大致相同,验证了理论计算测试距离的正确性。 同时,成像幅度逐渐减小,说明腔体内部反射值逐渐减小。方位角在0° ～59°范围内,金属腔体内部多次反射的RCS 比其他散射值大,在方位角为75°时,腔体内部反射小于近距离处腔体外表面镜像反射。验证了方位角在0° ～60°( -60° ～0°)范围内,腔体内部反射为腔体散射的主要部分,而方位角在60° ～90°( -90° ～-60°)范围内,腔体外壁散射影响逐渐变大。

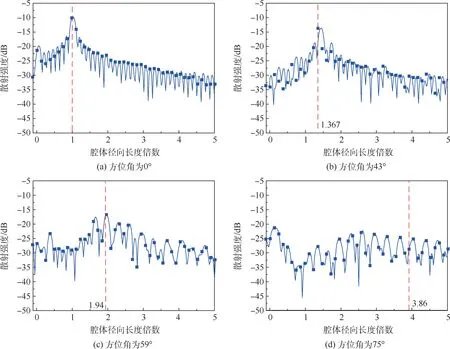
图10 不同方位角的一维距离像Fig.10 One-dimensional range profile at different azimuth angles

对于涂有吸波材料的腔体,同样在入射角为0°、43°、59°、75°做一维距离像,如图11 所示。

由图11(a)可知,随着方位角增大,散射距离增加,同时腔体散射量值逐渐减小。 由图11(b)可以看出,当腔体内壁涂有吸波材料时,方位角为59°时推算的最大散射距离应为0.6 m左右,但是其散射量值很低,可以忽略,方位角为75°时,腔体内部散射也可以忽略。 由此说明,对于内壁吸波材料性能良好的腔体,散射测量设备具备2 倍腔体径向长度的测量能力即可准确测量腔体散射。 但是,检验吸波材料性能是否良好也是测量的目的之一,所以,对于测量设备来说,应该具备2 ～5 倍腔体径向长度的测量能力,以应对吸波材料性能不好的情况。

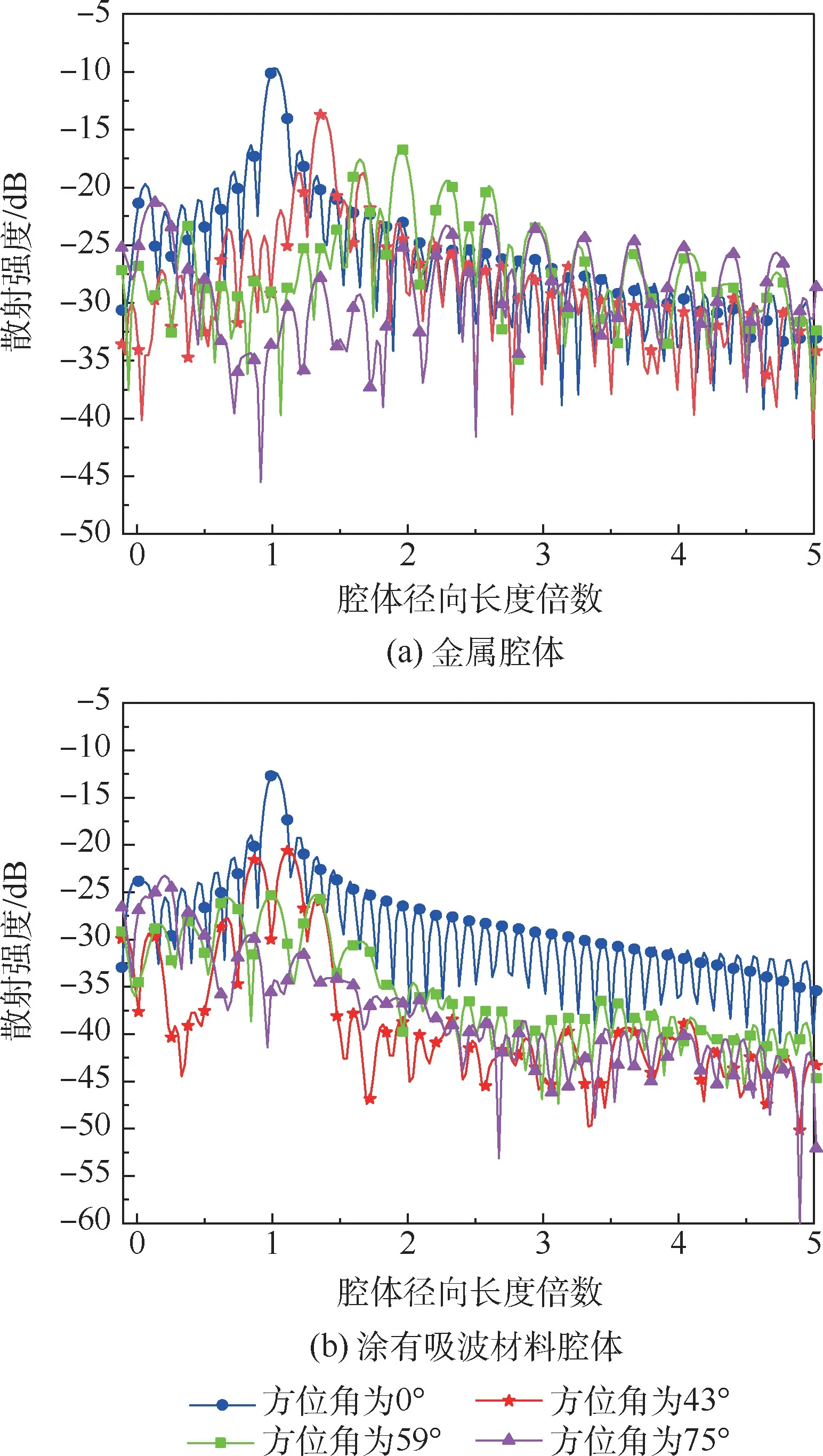
图11 水平极化状态下不同方位角的一维距离像Fig.11 One-dimensional range profiles at different azimuth angles under horizontal polarization

3 实验结果及分析

为了验证理论计算与仿真计算是否正确, 本节通过2 种类型的实验测量,分别验证是否应以口面尺寸计算进气道远场条件,以及长度方向满足远场条件的情况下,进气道的散射特性RCS 和散射测量系统配置的关系。

实验所用测试场,一种是北京航空航天大学2.5 m 静区的紧缩场,尺寸小于2.5 m 的目标在此紧缩场内都满足远场条件。 另一种是普通远场,需计算远场条件,实际测量中是在同一个实验室直接架设喇叭天线实现,天线至目标距离5 m ＜R＜7 m。

模型设计方面,因为验证的目标是腔体散射只与腔体口面场分布有关,与腔体外壁电磁散射无关。 因此,设计的模型使其口面尺寸满足远场条件,外壁即长度方向不满足远场条件。 在实验室天线至目标距离5 m ＜R＜7 m,信号频率f范围为5 ～15 GHz,波长0.02 m ＜λ＜0.06 m 时,目标尺寸应满足:

求得D＜0.224 m,0.224 m ＜L＜2.5 m。 据此结果,结合实际条件,选择口面尺寸D=0.11 m,长度L=0. 9 m。 按此尺寸,加工了方形腔体实验模型。

3.1 以口面尺寸计算远场条件

为验证以腔体口面尺寸计算远场条件是否合理,在紧缩场和普通远场条件下,对设计的腔体目标进行了频率为5 GHz 的RCS 测量。

测量场景如图12 所示。 其中图12(a)为紧缩场条件下进行测量,腔体口面和长度尺寸均满足远场条件。 图12(b)为普通远场条件下进行测量,腔体口面满足远场条件,而腔体长度不满足远场条件。

图12 不同条件下的实验测量系统Fig.12 Experimental measurement system under different conditions

2 种条件下的测量结果如图13 所示。 测试点频率为5 GHz,测试目标区长度为3 m,将待测目标放置在转台中央,通过计算机控制转台以0.5°为角度间隔转动360°( - 180° ～180°),共720 个角度位置。

从图13 可知,在方位角90°附近,即电磁波照射腔体模型长度最大尺寸时,普通远场RCS 曲线出现了典型的近场散射特征,与紧缩场测量结果有明显差别。 而在±60°小角度范围内,普通远场RCS 曲线与紧缩场测量结果基本一致。 而该角度范围内,散射机理以腔体散射为主,验证了腔体目标散射测量应以腔体口面尺寸计算远场条件的判断。

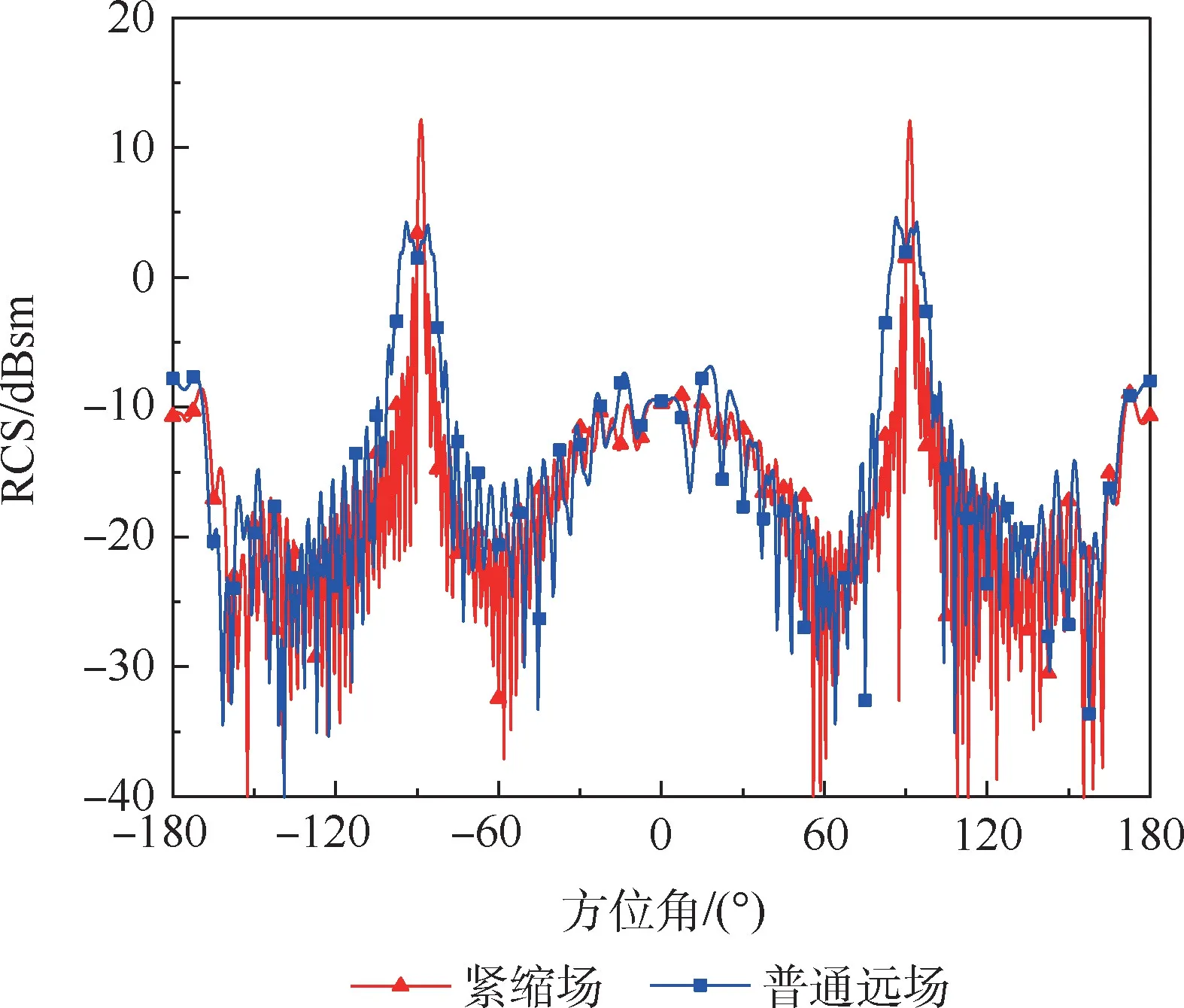
图13 方形腔体水平极化状态下紧缩场测量与普通远场结果比较Fig.13 Comparison of compact field measurement and ordinary far field measurement of square cavity under horizontal polarization state

3.2 满足远场条件情况下测量系统的配置

目前的主流散射测试场以紧缩场为主,在此情况下,只要进气道尺寸不超过紧缩场静区尺寸,则进气道口面和长度都满足远场条件,但这种情况下测量结果不一定能真实反映进气道散射,因为除了远场条件,RCS 测量结果还与测试系统相关。 在紧缩场建设时,测试系统一般都与紧缩场静区尺寸匹配,即2 m 静区的紧缩场,测量系统具备2 m 或3 m 目标的测量能力就基本达到要求。但是根据第1 节对腔体目标散射机理的分析,进气道等腔体类目标的散射机理主要是多次反射。理论推导与仿真验证结果表明,电磁波在腔体内的传播路径可达腔体长度数倍。 因此,如果在2 m静区的测试场中测量长度2 m 的进气道,而测量系统仅具备3 m 目标的测量能力,获得的进气道散射结果就可能有较大偏差。

在北京航空航天大学2.5 m 静区紧缩场中,对方形腔体长度0.9 m 的腔体进行了频率15 GHz的散射测量。 紧缩场静区远大于目标物理尺寸,满足远场条件。 但是在测量系统配置上,分别取1.5,2,2. 5,3 m 目标区进行RCS 计算,获得的RCS 曲线如图14 所示。

从图14 可知,取1.5,2,2.5,3 m 目标区进行RCS 计算获得的结果方位角在±60°范围外曲线一致性非常好,这是由于方位角在±60°范围外,腔体散射主要由腔体外表面散射为主,不存在多次反射。 而在方位角±60°范围内,取1.5,2,2.5,3 m目标区进行RCS 计算获得的结果差别非常大,可达10 dB 以上,但是1.5 m 目标区也达到了腔体物理尺寸的1.5 倍,按照一般目标考虑,基本满足测量要求。 出现如此大的曲线差别,只能判断是由腔体多次反射引起电磁波传播路径变长造成。

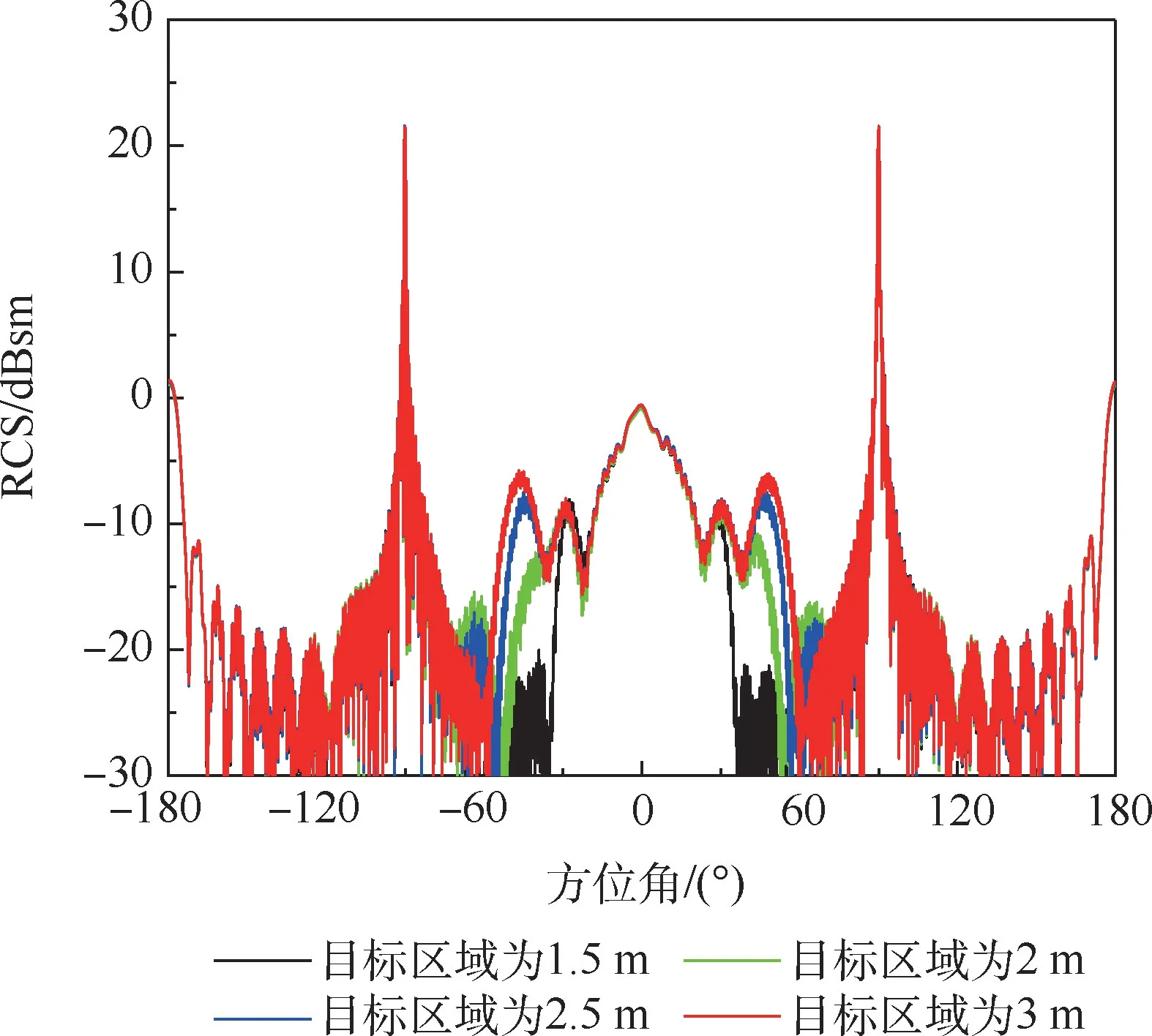
图14 频率15 GHz 方形腔体水平极化状态下的RCS 曲线Fig.14 RCS curves of 15 GHz square cavity in horizontal polarization state

为验证该问题,对腔体目标进行了二维成像诊断,如图15 所示。 其中测量频率范围为13 ～17 GHz,孔径角16°。

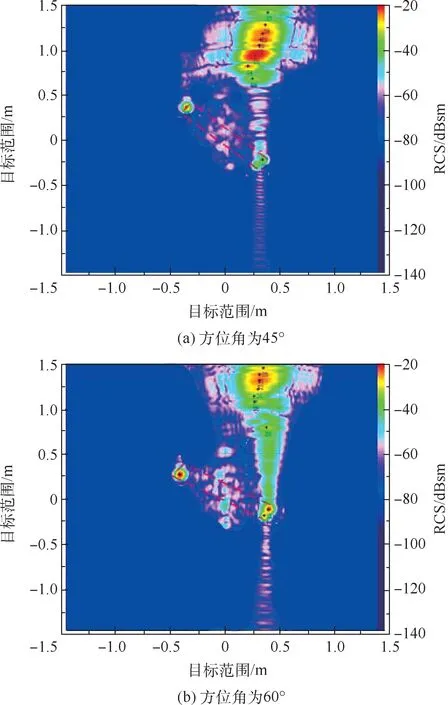
图15 方形腔体水平极化状态下不同方位角的二维成像Fig.15 Two-dimensional imaging of square cavity with horizontal polarization at different azimuth angles

如图15 所示,方形腔体在方位角为45°处,其最大散射源位置并不在腔体物理尺寸(图15中的红色虚线框处)所在位置,而是出现在腔体几何中心1.5 m 之后区域,而该位置处并没有实际目标存在,只能是腔体内部多次散射引起。 如果测量系统目标区配置不合理,很可能遗漏这一对腔体有重要贡献的散射分量。 方形腔体在方位角为60°处,其最大散射源位置在腔体口面处,这与腔体形状有关。 但是在腔体几何中心1.5 m 之后区域,仍然有很大的散射源存在。 这说明,测量方位角在±60°范围内,当取1.5,2,2.5,3 m 目标区对腔体目标进行RCS 计算,结果会差别非常大。

图15 的实验结果说明,即使在进气道口面和长度都满足远场条件的情况下,RCS 测量结果也未必能真实反映进气道的散射。 除了满足远场条件,测量腔体类目标散射时,测试系统还需根据腔体尺寸进行合理配置,根据仿真计算,测试系统应具备2 ～5 倍腔体径向长度的测量能力。

4 结 论

本文以方形腔体为例进行分析,研究方法基于电磁场基本规律,圆形腔体、S 弯进气道等其他腔体同样遵循这些规律,只是其他腔体的求解更为复杂,由方形腔体分析得到的测量要求也适用于其他腔体。 对于进气道等腔体类目标RCS 测量,其基本结论如下:

1) 腔体类目标散射测量用腔体口面尺寸计算远场条件,而不用尺寸更大的径向长度。 即长度5 m,口面尺寸1 m 的进气道,可以在静区尺寸1 ～2 m 的紧缩场中测量,前提是保证旋转过程中进气道口面在静区范围内。

2) 在进气道口面和长度都满足远场条件的情况下,RCS 测量结果也未必能真实反映进气道的散射,即在腔体实际物理尺寸之后仍然存在较强散射源。

3) 除了满足口面远场条件,测量腔体类目标散射时,测试系统应具备2 ～5 倍腔体长度的测量能力。 即长度5 m,口面尺寸1 m 的进气道,在5 m静区紧缩场中未必能获得准确测量结果,测量系统至少要具备测量大于10 m 尺寸目标的能力。