不同形状破片对945钢靶的侵彻性能的影响规律分析
2023-01-12李德聪
张 霄,李德聪
(中国舰船研究设计中心,湖北 武汉 430064)
0 引 言
目前反舰导弹大多采用半穿甲战斗部,可穿透舰船舷侧外板,进入舰船内部使其爆炸。一般而言,战斗部壳体的质量在战斗部总质量中的占比可达60%~65%,爆炸之后会产生大量高速运动的破片(初速度最高能超过2 000 m/s)[1-2],这些破片形状各异,毁伤威力极大,对于船上的重要舱室而言,需在其四周舱壁处设置装甲防护结构,以保证舱室内人员和设备的安全。
舰船装甲防护结构一般根据防护等级要求设计。不同防护等级规定了所要防御破片的质量和速度要求,但未对破片形状作统一的规定,对不同形状破片的侵彻性能的分析缺乏量化的对比数据,给装甲防护结构设计及其抗侵彻性能的横向对比带来了很大影响。苗春壮等[3]针对不同形状破片的破坏威力,通过分析不同形状预控破片的毁伤情况,认为正六边形破片的预控效果最好,没有产生相互粘连的破片,菱形破片存在少量双破片粘连,正方形破片和三角形破片存在多破片粘连;通过对破片侵彻钢靶进行仿真计算,得出在初速和质量相同的情况下,不同截面形状破片的杀伤威力由强到弱为正六边形、正方形、菱形和三角形。吴晓凤等[4]认为孔径大小通常可作为破片毁伤性能评估的标准之一,孔径较大可在一定程度上视为杀伤能力较强。因此,就孔径大小而言,立方体形破片的破孔能力最强,圆柱形破片次之,球形破片最弱。舰船装甲结构抗高速破片侵彻的过程是一个复杂的强非线性动态毁伤过程,具有穿甲时间短和载荷强度大的特点[5-11]。目前常用的装甲结构抗破片侵彻分析方法主要有试验法、经验法和数值仿真法,其中数值仿真法不仅成本较低,而且能较好地模拟破片穿甲过程中结构毁伤的细节,并能给出准确的破片剩余速度等关键数据,因此得到了广泛应用。本文采用ANSYS/LS-DYNA软件对球形、圆柱形(长径比为1.5)和立方体形等3种形状破片侵彻舰船945钢均质装甲结构的过程进行数值模拟,通过对比不同形状破片的弹道极限速度,获取其对945钢均质靶板的侵彻性能的影响规律,以期为舰船装甲防护结构设计提供参考。
1 破片侵彻靶板有限元模型
1.1 仿真对象
破片:材料为舰用945钢;质量为3.98 g;形状分别为立方体形、圆柱形(长径比为1.5)和球形。
靶板:材料为舰用945钢;形状为正方形;尺寸为240 mm×240 mm×8 mm;四周固支。
1.2 材料模型
在破片高速侵彻钢质靶板过程中,破片与靶板均存在明显的大变形和毁伤现象,因此在仿真计算中破片和靶板均采用Johnson-Cook材料模型(简称为J-C模型)模拟,该模型考虑了材料的应变率和温度效应,能很好地表征材料在侵彻过程中的塑性大变形和损伤破坏等力学行为,适于在金属由准静态转变为大应变、高应变率和高温状态的情况下应用。J-C本构模型的表达式为
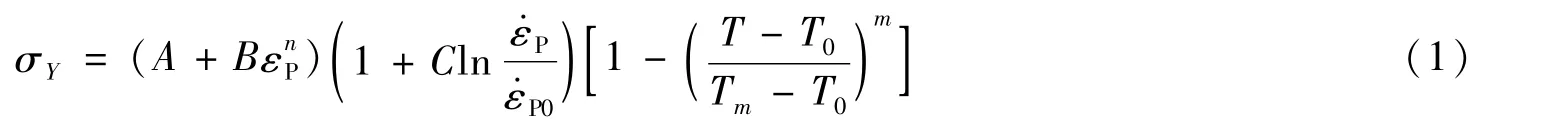
式(1)中,A为静态屈服极限;B为应变硬化模量;εP为塑性应变;为塑性应变率;T为温度;n为应变硬化指数;C为应变率系数;为参考应变率;Tm为材料的熔点;T0为参考温度;m为热软化系数。
破片和靶板的材料均为舰用945钢,其模型参数的取值参照文献[12],具体见表1,其中:E为弹性模量;υ为泊松比;ρ为密度。

表1 945钢的主要力学性能和J-C模型参数
1.3 数值仿真方法的准确性验证
为检验数值仿真方法的准确性,以侯海量等[13]开展的侵彻试验为例进行仿真模拟。该试验中的破片和靶板的材料均采用舰用945钢,通过将仿真结果与文献[13]中的试验数据相对比,检验数值仿真方法的准确性。试验中采用FSP形破片侵彻正方形靶板,具体数据如下。
1)FSP形破片:直径为14.8 mm;体长为20.449 mm;材料为舰用945钢;质量为26 g。
2)靶板:尺寸为800.00 mm×800.00 mm×3.92 mm;材料为舰用945钢。
破片和靶板的材料模型均采用J-C模型,将表1中的数据代入ANSYS/LS-DYNA软件中,单元采用SOLID164单元,接触方式采用面-面侵蚀接触方式。分别对FSP形破片以初速度1.067 5 km/s和1.238 8 km/s正侵彻靶板的工况进行模拟,图1和图2分别为2种初速度下破片侵彻靶板过程中靶板的毁伤模式图和破片速度的时历曲线。
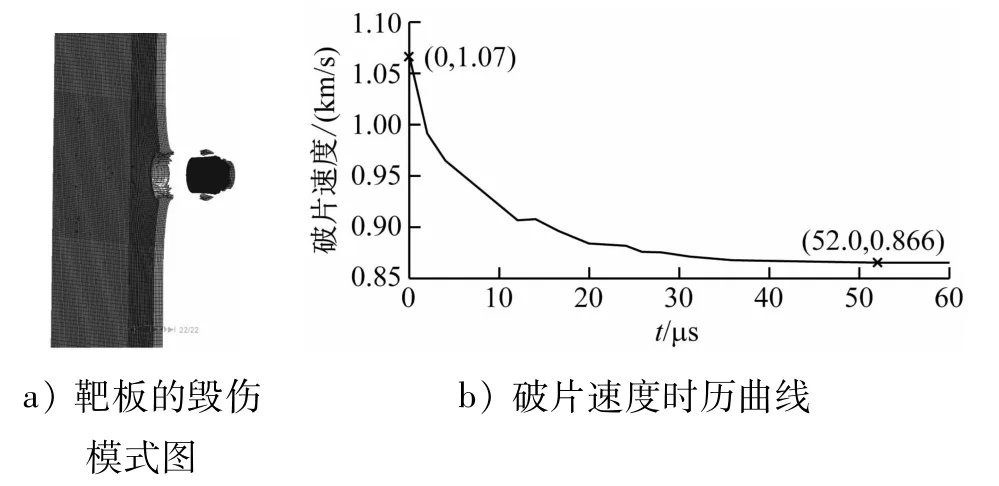
图1 破片初速度为1.067 5 km/s时靶板的毁伤模式图和破片速度的时历曲线
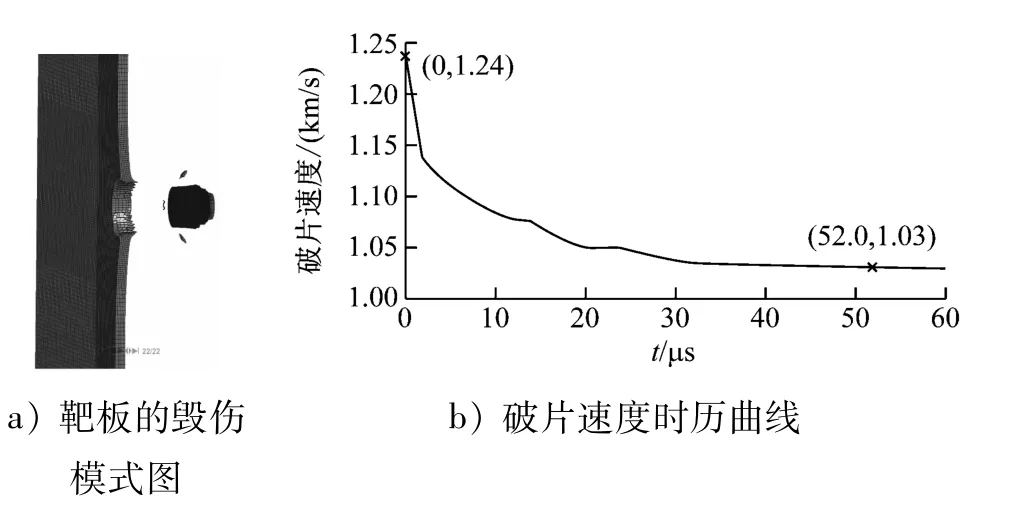
图2 破片初速度为1.238 8 km/s时靶板的毁伤模式图和破片速度的时历曲线
由破片速度时历曲线可知,FSP形破片以初速度1.067 5 km/s和1.238 8 km/s穿过靶板之后的剩余速度分别为0.866 0 km/s和1.030 0 km/s,破片剩余速度数值仿真结果与文献[13]中的试验数据对比见表2。

表2 破片剩余速度数值仿真结果与试验数据对比
从表2中可看出:数值仿真结果与文献[13]中的试验结果相比,偏差小于3%,说明本文采用的模型参数合理,数值仿真方法的准确性较好,可用来对不同形状破片侵彻钢靶的性能进行定量分析。
2 靶板抗侵彻性能表征
目前用于评价材料抗侵彻性能的主要参数有弹道极限速度和比吸能,其中比吸能又分为极限比吸能和贯穿比吸能。
2.1 弹道极限速度
弹道极限速度是指穿透靶板的临界速度,试验中因存在误差和不确定性,一般会进行多组穿靶试验,根据穿靶的概率和破片的速度建立极限速度测试方法。弹道极限速度与弹靶的基本参数(破片形状、质量、材料、密度和厚度等)密切相关,既能作为装甲防护的表征评价指标,又可作为特殊条件下对比防护材料的侵彻能力的参考量。
2.2 比吸能
比吸能是指靶板在侵彻过程中吸收的总能量与自身面密度的比值,反映相同质量下抗侵彻能力的强弱。比吸能可根据比式不同分为极限比吸能和贯穿比吸能,其中:极限比吸能是在速度为弹道极限速度v50的情况下靶板的吸能与面密度之比;贯穿比吸能是靶板在被破片贯穿过程中的吸能与面密度之比。
极限比吸能是在v50的基础上的深化表征量,v50能很好地反映不同靶板之间的抗侵彻能力,但会受靶板厚度和质量等因素的影响,而极限比吸能可很好地避免此类问题。但是,在固定板厚(面密度)情况下,极限比吸能与v50可等效。
根据贯穿比吸能的定义,破片在侵彻穿靶过程中损耗的动能应等于靶板的形变破坏能,因此在应用贯穿比吸能时需满足条件:破片在侵彻穿靶过程中无质量损耗,且保持刚性;忽略球膨胀效应和摩擦效应。这意味着要想通过贯穿比吸能表征靶板的抗侵彻能力,必须使破片的刚度远大于靶板的刚度。
综合来看,在弹道极限速度、极限比吸能和贯穿比吸能等3个表征量中:贯穿比吸能的要求较多,且需规避速度效应带来的吸能影响;极限比吸能是在弹道极限速度的基础上的深化表征量,相比极限速度能很好地避免厚度和质量问题带来的影响。在固定板厚(面密度)的情况下,极限比吸能与弹道极限速度可等效。因此,在此次数值仿真中将弹道极限速度作为表征靶板抗侵彻性能的参量。
3 不同形状破片穿甲性能有限元分析
3.1 有限元模型的建立
采用ANSYS/LS-DYNA对3种不同形状的破片侵彻靶板的过程进行模拟,破片和靶板均采用lagrange网格。为更好地对比不同形状破片的侵彻性能,使3种形状破片的质量保持一致,均为3.98 g。立方体形破片的边长为8 mm;圆柱体形破片的长径比为1.5,直径为7.574 mm;球形破片的直径为9.926 mm。靶板的尺寸为240 mm×240 mm×8 mm。破片和靶板均采用SOLID164单元,接触设置选择侵蚀接触,模拟破片在侵彻过程中的消蚀现象。当单元变形引起的损伤超过模型设定的损伤值时,认为此时单元已破坏,不再承载,避免了网格畸变导致计算不收敛的问题。破片的网格尺寸根据形状的不同划分为0.2~0.4 mm;靶板采取渐变式网格划分,中间侵彻区域网格细密,网格尺寸从中间向外侧逐渐变大。图3为破片和靶板网格划分模型。
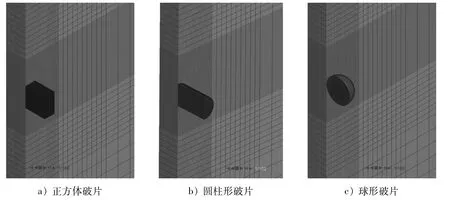
图3 破片和靶板网格划分模型
3.2 弹道极限速度计算方法
本文采用数值“逼近法”计算弹道极限速度,具体实现方式[14]如下。
1)建立破片和靶板有限元模型之后,赋予破片初速度进行侵彻过程仿真。
2)若靶板未出现穿靶现象,则适当增加下一发破片的速度;若靶板被穿透,则根据能量曲线得到靶板被穿透后的剩余能量。用初始能量减去剩余能量得到能量差,根据该能量差得到下一发破片的初速度。
3)进行数次仿真计算,直至穿透和未穿透2种情况下破片的初速度在允许范围内,取2发破片速度的平均值作为弹道极限速度。
图4为球形破片侵彻过程。

图4 球形破片侵彻过程

3.3 计算结果及分析
采用数值“逼近法”,针对8 mm厚的舰用945钢靶,分别求得立方体形、圆柱形(长径比为1.5)和球形破片的弹道极限速度,结果见表3。

表3 不同形状破片的弹道极限速度
数值仿真结果表明:3种形状破片的弹道极限速度由大到小排序为立方体形破片>球形破片>圆柱形破片,即圆柱形破片的侵彻性能最好,球形破片和立方体形破片次之;若以球形破片的侵彻性能为基准,则圆柱形破片(长径比为1.5)的侵彻性能提升了10.8%,立方体形破片的侵彻性能下降了11.9%。
3种形状破片在侵彻靶板之后的变形情况见图5。从图5中可看出:3种形状破片侵彻靶板之后的变形情况明显不同,由于在数值仿真中将破片视为变形体,因此破片在侵彻过程中发生一定的侵蚀,圆柱形破片的侵蚀比例明显小于球形破片和立方体形破片;圆柱形破片在侵彻过程中与靶板的接触面积最小,侵彻能量更集中,单位面积上的能量密度最大,因此其侵彻性能最好。

图5 3种形状破片在侵彻靶板之后的变形情况
3.4 穿靶机理分析
采用后处理软件LS-PREPOST对3种形状破片的侵彻过程作进一步的分析,根据不同时刻的应力云图和穿靶过程图像分析其破坏机理。图6为立方体形破片穿靶过程中靶板的应力云图。从图6中可看出:破片在接触靶板时其应力波就开始在靶板内由接触点向四周传播,破片的最大应力在破片头部位置,靶板的最大应力在靶板与破片接触的区域;随着破片继续侵彻靶板,破片的侵蚀情况越来越严重,在9 μs左右时破片已被侵蚀过半;随着破片逐渐被侵蚀,靶板上的弹坑逐渐缩小,整体被贯穿的区域呈圆台状。
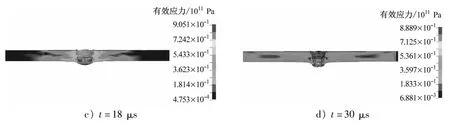
图6 立方体形破片穿靶过程中靶板的应力云图

图7为圆柱形破片穿靶过程中靶板的应力云图。从图7中可看出:圆柱形破片因弹身为细长型,其破片的侵蚀情况要明显好于立方体形破片;在9 μs左右时,破片被侵蚀不超过1/2;立方体形破片在侵彻靶板过程中所受应力要大于圆柱形破片,这是其在侵彻过程中更易发生变形和被侵蚀的原因。下面分析球形破片的侵彻过程。图8为球形破片穿靶过程中靶板的应力云图。
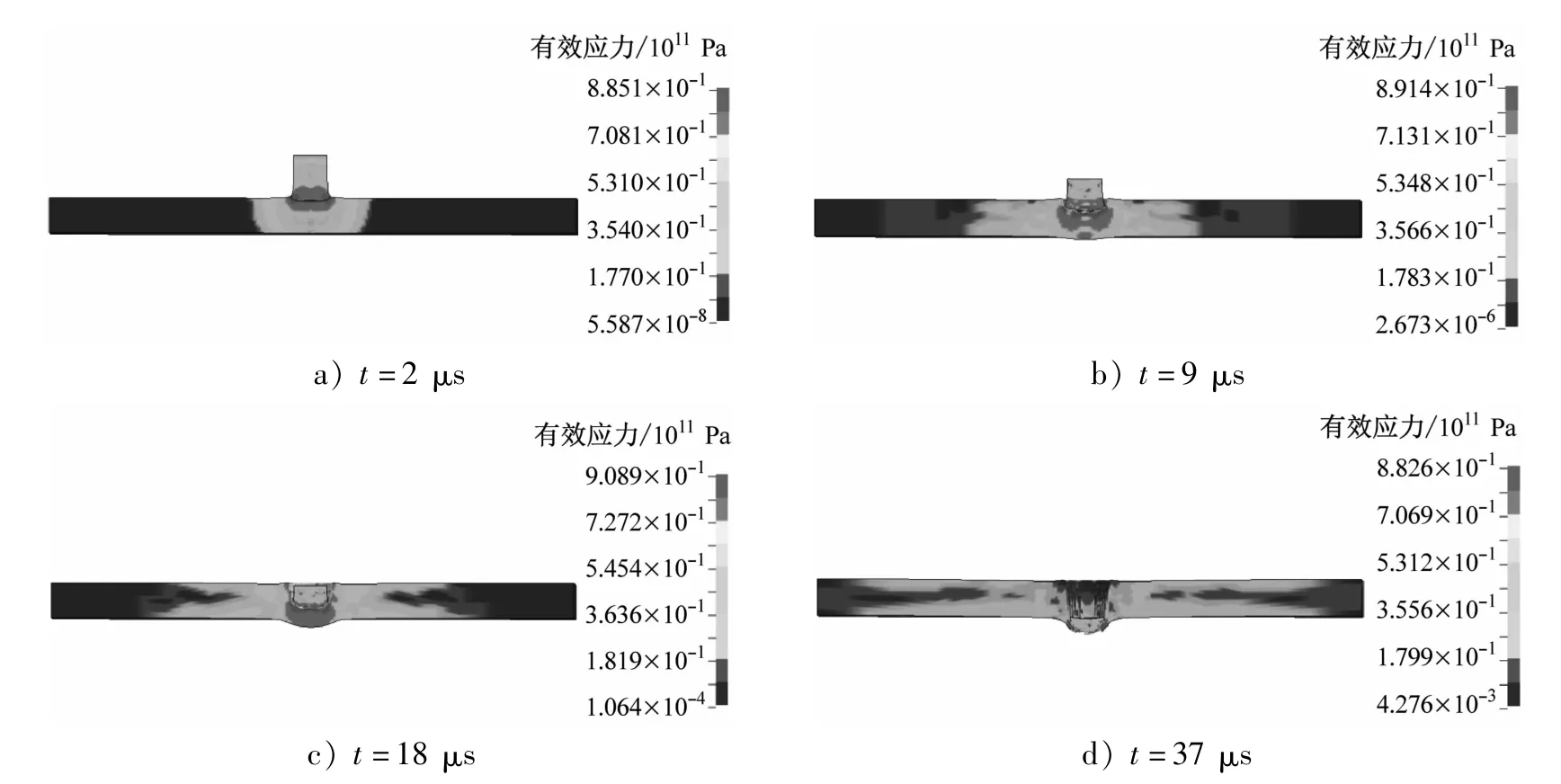
图7 圆柱形破片穿靶过程中靶板的应力云图

图8 球形破片穿靶过程中靶板的应力云图
通过对比图6~图8可知,在3种形状破片穿靶过程中,球形破片穿靶所用时间最短,其侵蚀情况虽然比圆柱形破片严重一些,但最终仍剩余较大体积,同样具备穿靶之后造成二次伤害的威力。总体来说,3种形状破片的侵彻过程较为相似,但在穿靶所用时间和破片侵蚀状况等方面存在一定的差异。
3.5 穿靶耗能分析
为进一步探究不同形状破片的侵彻性能,计算得到3种形状破片在不同初始速度下的穿靶动能消耗Ec,计算公式为
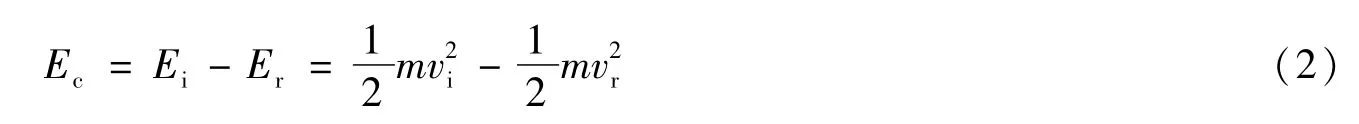
式(2)中:Ei为破片初始动能;Er为破片剩余动能;m为破片质量;vi为破片初始速度;vr为破片剩余速度。根据式(2)求得3种形状破片在不同初始速度下的穿靶动能消耗Ec见表4。

表4 3种形状破片在不同初始速度下的穿靶动能消耗Ec
图9为3种形状破片在不同初始速度下的穿靶耗能Ec的变化曲线。由表4和图9可知:破片的侵彻性能越好,其消耗的穿靶动能越少,且穿靶耗能受破片初始速度的影响较小;立方体形破片的侵彻性能最差,侵彻过程中消耗了大量能量,且因在侵彻过程中变形较大,穿靶耗能受破片初始速度的影响较大。
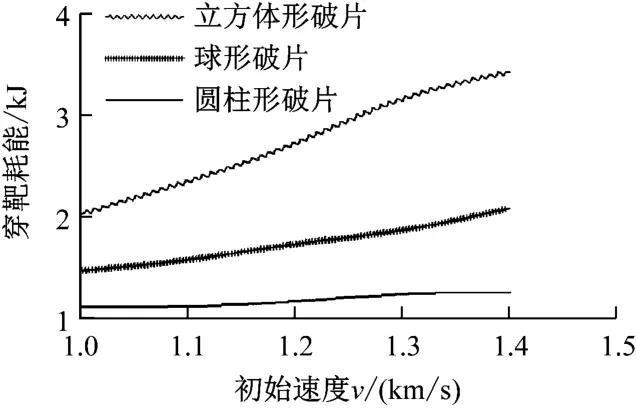
图9 3种形状破片在不同初始速度下的穿靶耗能Ec的变化曲线
4 结 语
通过对不同形状破片侵彻靶板进行数值仿真计算分析,可得到以下结论:
1)3种形状破片的弹道极限速度由大到小排序为立方体形破片>球形破片>圆柱形破片,即圆柱形破片的侵彻性能最好,球形破片和立方体形破片次之;
2)对于不可视为刚性体的破片来说,圆柱形破片的侵蚀比例要明显小于球形破片和立方体形破片,与靶板的接触面积最小,侵彻能量更集中,因此其侵彻性能最好;
3)3种形状破片的侵彻过程相似,但在穿靶时间和侵蚀状况等方面存在一定的差异,其中,球形破片的穿靶时间最短,圆柱形破片的剩余体积最多,其二次伤害威力最大;
4)破片的侵彻性能越好,其消耗的穿靶动能越少,且穿靶耗能受破片初始速度的影响较小。
