优化运算策略 减少代数运算
2023-01-11江苏省石庄高级中学
江苏省石庄高级中学
张 进
数学运算是思维能力与运算技能的有机结合,是六大数学学科核心素养之一,更是高考数学考查的四大能力之一,在函数、数列、三角函数、立体几何、解析几何等相关内容中都占据着重要位置.高考数学试题中70%以上的试题都具有一定的运算量,因而,合理研究试题特点、了解算理、改进方法、优化策略,减少高考数学试题的运算是赢得考试成功的一大重要途径.下面结合实例,谈一谈在教学中如何优化解题策略,切实减少代数运算,综合提升复习效益.旨在抛砖引玉.
1 回归本质,直达要害
抓住问题的本质,包括相关问题的概念、定义、公式、公理、定理、几何意义等,抽象出对应问题的本质属性,直接利用相关问题的实质,直达要害,可以大大减少运算量,提升解题效率.
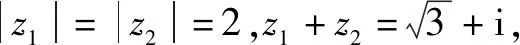
分析:引入两复数的和所对应的第三个复数,在复平面内,回归问题本质,根据复数的几何意义确定平面几何图形的特征,结合菱形的几何性质,以及两复数差所对应的图形元素来确定所求两复数差的模.
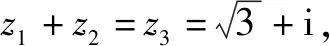
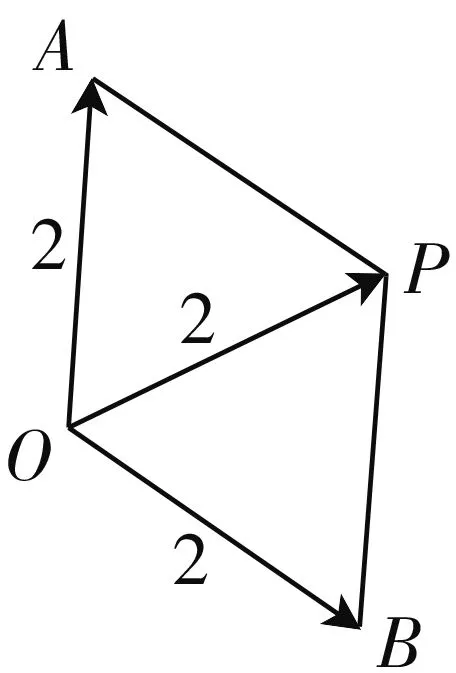
图1

点评:根据复数代数运算的几何意义,结合对应平面几何图形的特征,可以快捷破解有关复数的加、减等对应运算问题.结合几何意义,可以有效回归问题本质,挖掘问题内涵,简化运算.
2 数形结合,以图助算
数形结合思想是中学数学最重要的基本思想方法之一,更是历年高考数学考查的重点之一.利用数形结合思想,有效增加解题过程的直观性,直观想象,以图助算,可以大大减少运算量,提升解题效率.
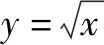
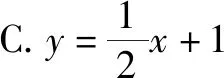
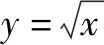
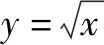
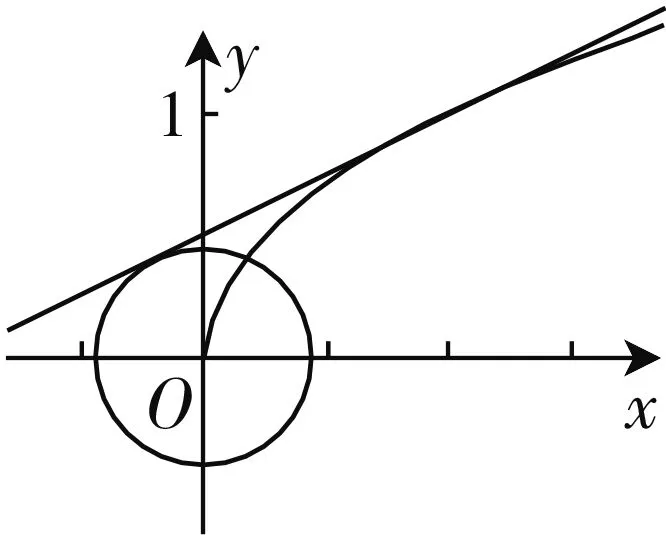
图2
同时切线l的斜率为正数,且小于1,可以直接排除选项B.
故选:D.
点评:直接从熟知的基本曲线图形入手,通过数形结合以及对应选项的特征分析加以排除与选择.利用数形结合直观处理相关问题时,往往图形都是比较熟知且较方便作出的,大致草图偏差只要不太大,就可以直观形象分析,简单快捷.
3 把握性质,合理建构
相关知识的基本性质是对该知识的理解、掌握、综合、应用的深入与拓展,准确把握基本性质,构建合理数学模型与关系,引入相应的参数、变量、模型等,合理建构,直接明确运算目标,可以大大减少运算量,提升解题效率.
例3(2020年高考数学江苏卷第11题)设{an}是公差为d的等差数列,{bn}是公比为q的等比数列.已知数列{an+bn}的前n项和Sn=n2-n+2n-1(n∈N*),则d+q的值是______.
分析:正确把握数列的函数性质,结合两特殊数列所对应的和式的函数表达式,构建函数表达式中对应的参数,建立相应的方程,借助系数的对比来确定,进而有效确定数列中公差d与公比q的值.
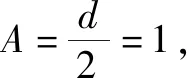
故填答案:4.
点评:正确把握等差数列与等比数列和式的函数基本性质,其中等差数列的前n项和公式Sn=An2+Bn,等比数列的前n项和公式Sn=C(qn-1),利用方程的建立与系数的对比,简捷地处理对应的值问题,很大程度上减少代数运算量,优化过程,提升效益.
4 特殊取值,估算取舍
对于一些数学客观题,借助特殊取值,根据特殊值(数或式)这一基本数学模型的选取与构造,可以用来破解参数值、函数值、代数式等的大小比较,以及不等式的求解与判定等问题,可以大大减少运算量,提升解题效率.
例4(2020年高考数学北京卷第6题)已知函数f(x)=2x-x-1,则不等式f(x)>0的解集是( ).
A.(-1,1) B.(-∞,-1)∪(1,+∞)
C.(0,1) D.(-∞,0)∪(1,+∞)
分析:通过选取特殊值,结合函数值的求解与不等式的比较来处理,估算取舍,一步到位,优化过程,减少运算量,简单快捷.
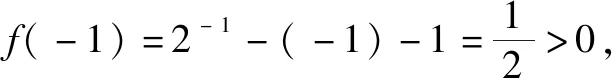
故选:D.
点评:借助特殊取值(数或式)的应用,结合排除法加以估算取舍,在解答一些客观题时,有一定的用武之地,简单易操作,且很大程度上避开了公式的应用和复杂的运算,减少数学运算,快捷准确.只是相应特殊取值(数或式)的选取有一定的技巧和局限性.
5 合情推理,弱化运算
在破解一些相关的数学问题时,借助合情推理,可以在很大程度上优化代数运算的步骤,简化数学运算的过程,弱化数学运算,从而有效减少出错的机会,提升问题的准确率与破解问题的效益.
例5(2020年高考数学全国卷Ⅰ理科第12题)若2a+log2a=4b+2log4b,则( ).
A.a>2bB.a<2bC.a>b2D.a 分析:根据条件对指数、对数问题进行同底化恒等变形,结合函数的构造以及函数单调性的应用,合情推理,巧妙转化,进而利用函数的单调性、不等式的基本性质等来确定相关参数的大小关系. 解析:由于2a+log2a=4b+2log4b=22b+log2b,构造函数f(x)=2x+log2x,则知函数f(x)在区间(0,+∞)上单调递增.又因为f(2b)=22b+log2(2b)=22b+log2b+1>22b+log2b=2a+log2a=f(a),可得a<2b. 故选:B. 点评:合理变形与转化,合情推理论证,借助函数性质来分析与判断参数的大小关系.在解答数学问题中,不能只是埋头苦算,要注意合情推理,增加解答过程的“含理量”,优化过程,减少运算,特别在大小比较以及立体几何与代数推理等问题中有奇效. 高考数学中对数学运算能力的考查是多角度、多方位、多层面的,尤其重视对数学运算算理的考查,很多高考试题需要根据不同的情况加以灵活处理.因而,平时教学学习与解题过程中,一定要注意数学运算的策略与方法,能避免的代数运算就尽量避免,不能避免的代数运算一定要注意运算的合理性、简捷性和准确性,这样才能在高考中优化运算,提升效率,立于不败之地.
