摸球问题 有型可循*
2023-01-11福建省石狮市第一中学
福建省石狮市第一中学
李桂娟
在古典概率问题中,有一类物品抽取问题,其概率的计算较为困难,如抽签、随机取数、次品抽取等.但如果能建立某种模型,将要解决的概率问题通过适当的转化,让它适用于该模型,往往能使问题更清楚,更容易看出问题本质.
引例一个袋子内有6个大小一样的小球,其中4个是黑球,2个是白球.
(1)从中任意取出3个球,求既有黑球又有白球的概率;
(2)从中不放回地依次取出3个球,求第三次摸到白球的概率;
(3)从中有放回地依次取出3个球,求第三次摸到白球的概率.
分析:以上三个问题,分别代表了古典概型中摸球问题的常见三种类型.
(1)一次性摸取.
摸球的特点:一次性摸取,元素不重复,无顺序.解决的方法:组合的思想.
(2)逐次、每次不放回摸取.
摸球的特点:逐次、每次不放回摸取,元素不重复,但有顺序.解决的方法:排列的思想.
(3)逐次、每次有放回摸取.
摸球的特点:逐次、每次有放回摸取,元素重复,同一个球每次被摸到的概率都一样.解决方法:独立重复试验中某事件发生的概率不变.

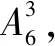
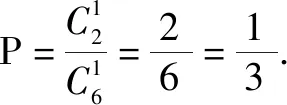

为了方便起见,把上述的第一种类型(一次性摸取)和第二种类型(逐次、每次不放回摸取),统称为不放回摸球模型.第三种类型(逐次、每次有放回摸取),称为有放回摸球模型.
模型的析出:
不放回摸球模型——解决的方法:组合或排列的思想.
有放回摸球模型——解决的方法:独立重复试验中某事件发生的概率不变.
在不放回摸球模型和有放回摸球模型中,最后一次摸到白球的概率是一样的.能否得到一般性的结论?
变式1一个袋子内有a+b个大小一样的小球,其中a个是黑球,b个是白球.
(1)从中不放回地依次取出k个球(1≤k≤a+b),最后一次摸到白球的概率为多少?
(2)从中有放回地依次取出k个球(1≤k≤a+b),最后一次摸到白球的概率为多少?
分析:变式1是引例的推广.
解:(1)问题等价于“从a+b个球中任意取出k个球进行排列,求第k个球是白球的概率”,所求概率
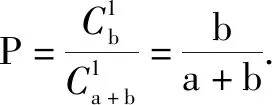
反思:在不放回摸球模型和有放回摸球模型中,第k次摸到白球的概率是一样的.但是思考的方式却不同.在有放回摸球模型中,每次摸到白球都是独立的,从而只考虑第k次即可,不需要考虑前面k-1次摸球的情况;在不放回摸球模型中,前一次摸球会影响后一次摸球,所以整个摸球过程要当成一个整体考虑.
变式2(高考题改编)已知6只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性的即没患病.下面是两种化验方法:
方案甲:逐个化验,直到能确定患病动物为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验这3只,直到能确定患病动物为止;若结果呈阴性则表明患病动物为另外3只中的1只,然后再逐个化验另外3只,直到能确定患病动物为止.
(1)用X表示依方案甲所需化验次数,求X的期望;
(2)用Y表示依方案乙所需化验次数,求Y的期望.
分析:这是一道以摸球为背景的概率问题.
问题等价于:有6个大小一样的小球,其中5个是黑球,1个是白球.
方案甲:依次不放回地摸球,直到能确定摸出白球为止.
方案乙:从中任取3个球,若这三个球含白球,则继续从这3个球中依次不放回摸球,直到能确定摸出白球为止;若这三个球不含白球,则继续从另外含白球的3个球中依次不放回地摸球,直到能确定摸出白球为止.
属于不放回摸球模型.解决的方法:组合或排列的思想.
解:化验次数X的所有可能取值是1,2,3,4,5.
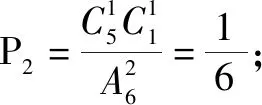

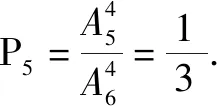
因此,方案甲所需化验次数X的数学期望
(2)化验次数Y的所有可能取值是2,3.
当Y=2时,有两类:
第一类,第一次任取的3只是含患病的,则继续从这3只中逐个化验,第一次就抽到患病的;
第二类,第一次任取的3只是不含患病的,则继续从另外含患病的3只中逐个化验,第一次就抽到患病的.
这两类事件互斥,概率为
同理,当Y=3时,也有两类:
第一类,第一次任取的3只是含患病的,则继续从这3只中逐个化验,第一次抽到不患病的,第二次不论是抽到不患病的还是抽到患病的,都能确定哪只是患病动物,化验结束;
第二类,第一次任取的3只是不含患病的,则继续从另外含患病的3只中逐个化验,第一次就抽到不患病的,第二次不论是抽到不患病的还是抽到患病的,都能确定哪只是患病动物,化验结束.
这两类事件互斥,概率为
因此,方案乙所需化验次数Y的数学期望
反思:本题也可以从对立事件的角度来求X=5与Y=3的概率.
研究以摸球为背景的概率问题,我们可以在解题中以如下思路思考问题:不放回摸球模型解决的方法是利用组合或排列的思想;有放回摸球模型解决方法是利用独立重复试验中某事件发生的概率的不变性.善于利用对立事件,是探求解题捷径的重要手段之一.
在摸球情景下,正确地求解概率问题,必须要具备一定的排列组合知识,熟悉并掌握必要的“概率模型”,会灵活运用分类与讨论、化归与转化等数学思想.
