一题一课 以题研课

江苏省宜兴市张渚高级中学

陈云明

课堂是教学的主阵地，数学课堂应该有一定的广度、深度，特别是高三复习课，更要精心选好试题，针对知识点，完善知识结构，激活学生思维，提升探究能力.其中，“一题一课”教学是高三数学复习课中一种非常重要的表现形式，对“题”进行深度挖掘，以“原题”为本，根据学生的认知规律和知识结构，合理设置，巧妙引导，从多层面进行“一题多解”尝试，从多角度进行“一题多变”创新，由浅入深，做一题，得一法，会一类，通一片.

1 一题多解

一题多解是在教师精心挑选下，利用同一道题目引导学生用不同的思维方法来破解，利用发散、联想、类比等思维方法对题目进行多角度、多方位的分析与思考，利用不同的知识、方法、工具等来分析与处理问题.一题多解能有效促进数学知识之间的联系，提升数学思维能力、创新能力与应用能力等.

例1(2020年高考数学江苏卷第11题)设{an}是公差为d的等差数列，{bn}是公比为q的等比数列.已知数列{an+bn}的前n项和Sn=n2-n+2n-1(n∈N*)，则d+q的值是______.

分析：此题是以两个特殊类型的等差数列与等比数列加以融合与交汇，结合数列{an+bn}的前n项和的表达式来确定对应数列的公差d与公比q的和式的值问题.

思维视角一：代数运算.

解法1：(代数运算法)当n=1时，S1=a1+b1=1-1+2-1=1；

当n≥2时，an+bn=Sn-Sn-1=n2-n+2n-1-[(n-1)2-(n-1)+2n-1-1]=2n-1+2n-2.

则有a2+b2=22-1+2×2-2=4，a3+b3=23-1+2×3-2=8，a4+b4=24-1+2×4-2=14.

于是a1+d+b1q=4，a1+2d+b1q2=8，a1+3d+b1q3=14.

将a1+b1=1与以上三式依次对应相减，可得

d+b1(q-1)=3，d+b1q(q-1)=4，d+b1q2(q-1)=6.

即b1(q-1)=3-d，b1q(q-1)=4-d，b1q2(q-1)=6-d.

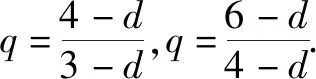
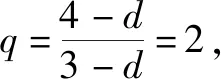
故填答案：4.

点评：通过n的分类讨论以及数列{an+bn}的前4项的确定，结合a1+b1=1与相应的关系式进行代数运算，并结合条件关系式的转化建立相应的方程，从而得以确定d与q的值.其实，在确定an+bn=2n-1+2n-2时，分别利用等差数列与等比数列的函数性，直接得以确定an=2n-2，bn=2n-1，进而确定公差与公比的值，在解决小题时可以这样处理，节省时间.

思维视角二：公式应用.

解法2：(对比系数法)设等差数列{an}的公差为d，等比数列{bn}的公比为q，根据题意知q≠1.

则等差数列{an}的前n项和公式为

等比数列{bn}的前n项和公式为

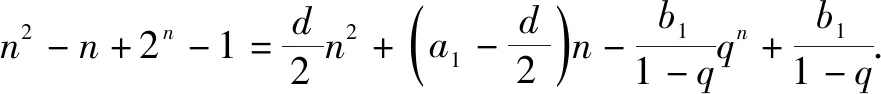
所以d+q=2+2=4.

故填答案：4.

点评：根据等差数列与等比数列的前n项和公式建立相应的关系式，结合条件Sn=n2-n+2n-1，通过对比相应数列求和中的系数关系建立对应的方程组，进而得以确定相关参数d与q的值.

2 一题多变

一题多变是在教师精心安排下，在实际教学过程中，以一道典型例题为模板，在解决问题的基础上再从多角度、多方位、多层面等思维视角提出不同的问题，以进一步加深学生对知识的理解和掌握.一题多变能有效促进数学知识、思想方法和能力的融会贯通、举一反三、触类旁通，培养创新思维与创新意识，提升创新能力与核心素养.

故选：D.

变式方向1：改变题目中的相关数据，难度相当.

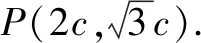
故选：B.

变式方向2：改变圆锥曲线的类型，难度相当.

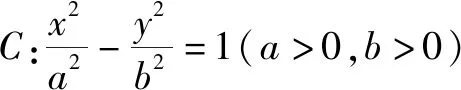
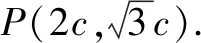
故选：B.

变式方向3：改变题目已知条件，难度相当.

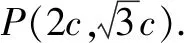
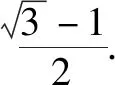
通过“一题多变”，培养学生的转向机智及思维的应变性，实现提高发散思维的变通性.

“一题一课”教学，借助一题多解，一题多变等方式，合理达到一题一练一测一思一小结.以问题驱动为导向，教师体现主导作用加以合理引导.充分体现学生的主体地位，知识尽可能让学生回顾，思路尽可能让学生探寻，方法尽可能让学生寻找，变式尽可能让学生尝试，从而真正实现知识回顾问题化，思路探寻发散化，方法寻找多样化，变式尝试创新化，全面提升数学能力，提高思维品质，培养数学核心素养.