热电材料中的电子输运机制及调控

张馨月，陈志炜，李 文，裴艳中

(同济大学材料科学与工程学院 材料交叉学科研究中心, 上海 201804 )

1 前 言

热电能量转换技术是一种通过温差驱动材料中载流子定向运动，实现热能和电能之间直接转换的清洁、无碳、可持续型的能源技术[1]。该技术具有无传动部件、全固态、零排放、零维护需求等优点，在航空航天、军事国防、微电子器件等领域具有广泛应用前景。热电器件的转换效率是评价其性能优劣的重要指标，热电转换效率主要取决于热电材料的无量纲热电优值zT(zT=S2σT/κ)，其中，S是塞贝克(Seebeck)系数，σ是电导率，κ是热导率，T是绝对温度。

热电优值表达式的分子S2σ被称为功率因子(power factor)，决定了热电器件的输出功率；而分母κ则对应于热电材料的导热性质，决定了流经热电器件的热流密度。主流的热电材料多为固态半导体，决定其功率因子的电传导媒介为电子，而热传导媒介主要是声子(晶格热导率κL)和电子(电子热导率κE)。因此，热电材料研究中提升性能的各种调控手段的本质是对材料中的电子、声子输运行为的调控。理想的热电材料应具有高的塞贝克系数与电导率，以及低的热导率。

在热输运方面，自20世纪50年代开始，以Ioffe为代表的热电先驱们提出了通过抑制声子热传导、降低晶格热导率来提升材料热电性能[2, 3]。此后的大量研究也表明，晶格热导率可以相对独立地被调控和优化，通过降低材料的晶格热导率或寻找具有本征低晶格热导率的材料是获得高性能热电材料的有效方法[4, 5]。在电输运方面，塞贝克系数和电导率通过载流子浓度强烈地互相耦合[6]，此消彼长，使得电输运性质的调控主要包括两个方向：一是通过优化载流子浓度获得功率因子的峰值[7-10]；二是通过能带调控等手段部分解耦塞贝克系数和电导率对载流子浓度的依赖[11-14]，实现功率因子的整体提升。

本文将从玻尔兹曼输运方程出发，结合无机半导体材料能带理论，重点阐述热电材料电输运行为的调控机制及方法，详细介绍近年来围绕热电材料性能提升而开展的电输运调控的研究进展。

2 热电材料中电子输运机制及调控原理

(1)

其中，e表示一个自由电子携带的电荷量，E为电子的能量，系数1/3表示电子运动的空间自由度(三维空间)，g(E)表示态密度，vg表示电子群速度，τ表示电子的弛豫时间，f表示费米-狄拉克分布函数。态密度与电子分布函数决定了电子数量的多少，电子群速度决定了电子运动的快慢，而弛豫时间则可形象地理解为电子运动可以维持多长时间。通过对以上各项参数的电子能量依赖关系进行分析，能够直观地看出固体中的电子导电行为。更重要的是，可以直观地看出各类性能调控方法的立足点。

为了简化讨论，假设电子具有抛物线型单一能带且散射过程由声学声子主导(SPB-APS近似)[15]。此假设的主要依据有3点：

(1)在自旋轨道耦合和轨道杂化效应较弱时，抛物带假设可以较好地描述许多热电材料，如Mg2Si[16]、half-Heusler[17]、Zintl[18, 19]等。对于一些非抛物带的典型热电材料，如PbTe、SnTe等，尽管抛物带近似丢失了部分能带结构信息，但简并度、有效质量等能带结构主要信息仍然被保留了下来。抛物带近似使得计算更加统一、材料与材料之间可以进行更好地进行比较；

(2)由于材料中电子和空穴两种载流子共存会导致其热电性能的急剧下降，具有优良性能的热电材料通常为重掺杂的宽带隙半导体[20]，因此暂不考虑电子和空穴两种载流子共存的情况；

(3)室温时电子的波长为～10-8m，大于一般晶格常数，因此晶格振动中波长较长的声学声子对载流子的散射起主导作用[21]。这也符合大部分中高温热电材料的实际情况，而额外的散射过程通常使材料的热电性能恶化[22, 23]。

(2)

(3)

可以看出，塞贝克系数中的分母为电导率，而分子是塞贝克导率，因此塞贝克系数即熵流与电流的比值。

由图1右上可以看出，电导率的绝对值(右图的积分面积)总是正的，且位于费米能级附近的电子对电导率的贡献最大；在电子态密度为零时，费米能级附近没有电子态，无法贡献电导。这对应了固态材料的导电特性：金属材料的费米能级深处于能带内部，导电能力很强；绝缘体的费米能级位于禁带中心，费米能级附近没有电子态，导电能力很弱；而半导体则介于两者之间。

由图1右下可以看出，塞贝克导率与电导率不同，位于费米能级两边的电子的塞贝克导率符号相反。对于金属材料，其费米能级深处于能带内部，位于费米能级两侧的塞贝克导率相互抵消，同时由于较高的电导率，使得其塞贝克系数通常很低；绝缘体的费米能级位于禁带中心，塞贝克导率没有正负抵消，电导率也低，因此绝缘体通常具有高的塞贝克系数；同样地，半导体的情况介于金属和绝缘体之间。结合电导率的分析，可得出高热电性能的材料通常是半导体，而不是金属或绝缘体的一般性结论。

图1 电势梯度、温度梯度所引起的电导率、塞贝克导率，以及其中各参量与电子能量的依赖关系[24]Fig.1 Transport functions of electrical conductivity and Seebeck conductivity clearly showing energy dependence of each parameter[24]

根据以上分析，可知影响热电材料电导率和塞贝克系数的参量包括电子态密度、电子速度和弛豫时间。因此，后文将分别综述并讨论围绕以上3个参量进行电输运调控的研究进展。

3 电子态密度调控

在玻尔兹曼输运框架下，调控热电输运性质可以从改变态密度的绝对值与形状两方面入手，如图2所示[25]。提高态密度的绝对值可显著提高参与输运过程的载流子浓度，从而在单位电场/单位温场驱动下获得更高的电流密度，具体体现为电导率与塞贝克导率的提高。而另一方面，增强态密度对载流子能量的依赖程度可显著增大费米面之上的高能载流子与费米面之下的低能载流子之间的浓度差，从而在单位温场下获得更高的净熵流密度，具体体现为塞贝克导率与塞贝克系数的提高。

热电材料电学性能的调控手段之一是围绕载流子态密度的设计而展开。近年来的研究重点之一是如何在不显著改变塞贝克系数的情况下显著提升热电材料电导率，反之亦然。针对这一思路，后文着重介绍热电材料中载流子态密度的设计方法。

3.1 能带简并

在一般的半导体材料中，可以将多条能量极值相近(通常在几个kBT以内)的能带看成是简并的(如图2a所示)，主要可细分为轨道简并和能谷简并[25]。

图2 能带简并(a)及共振能级(b)对态密度影响示意图[25]Fig.2 Schematic diagram of the density of states of a band (dashed line) contrasted to that of band convergence (a) and resonant level (b)[25]

轨道简并是指主量子数与角量子数都相同而磁量子数不同的能带极值点在能量上没有差异或差异非常小。以Mg3Sb2为代表的CaAl2Si2型Zintl化合物[26, 27]是具有该特点的典型热电材料体系。Zintl化合物的价带结构由阴离子的p轨道决定，其价带结构不像立方材料那样在Gamma点有三重简并的p轨道，Zintl化合物的三方(或其他非立方)结构使得其pz与px/py轨道在晶体场的作用下发生劈裂[26, 28]，此时pz与px/py轨道的能量差也称为轨道劈裂能Δ(如图3a和3b所示)。显然，当轨道劈裂能接近0时，轨道简并度最高，这对提升载流子态密度、热电材料的电输运性能至关重要。CaAl2Si2型Zintl化合物中p轨道的晶体场劈裂源于其非立方的晶体结构，因此调控劈裂能的有效方法之一是通过固溶调控晶体结构的畸变程度[29]。通过该方法在p型的YbCd2Sb2[30]、EuCd2Sb2[31]、CaMg2Bi2[32]、Mg3Sb2[33]等热电材料中都实现了轨道简并度的提升以及热电性能的增强。

Mg2Si1-xSnx也是具有轨道简并效应的典型体系。Mg2Si和Mg2Sn的第一导带和第二导带都位于布里渊区中的X点[34]。在Mg2Si中，轻带(XL)为第一导带，在重带(XH)之下，而Mg2Sn中则相反，重带为第一导带，在轻带之下[35, 36]。当两者形成Mg2Si1-xSnx固溶体时，轻带和重带的能量会随着组分变化而变化，在x=0.6～0.7时，发生简并。理论[37]和实验研究[38, 39]都证明了这种能带简并效应对Mg2Si1-xSnx热电性能的提升有益，并且这种固溶同时也能降低晶格热导率[40, 41]。相较于Mg2Si和Mg2Sn，Mg2Si1-xSnx合金(x=0.6～0.7)的热电性能获得了大幅提升[38, 42]。类似效应在Mg2Sn1-xGex体系中也得到了证明[43, 44]。

除轨道简并之外，能谷简并也是调控载流子态密度的有效方案。能谷简并是指：能带极值点位于布里渊区中的高对称点，具有>1的等同位置且它们之间完全等价，具有该特点的典型热电材料体系是以PbTe为代表的IV-VI族化合物[25, 45]。PbTe第一价带极值点在布里渊区边界的L点上，有8个等价的位点，因此简并度Nv=4；而第二价带极值点在布里渊区内的Σ方向上，有12个等价的位点，因此简并度Nv=12，这两个价带之间的能量差仅～0.2 eV[46, 47]。降低L带能量或提升Σ带能量，使得L带和Σ带能量差减小，能谷简并度Nv最高可达16(图3c和3d所示)[12]，此时热电材料电学性能有望获得显著提高。

图3 CaAl2Si2型Zintl化合物轨道简并及阴离子的p轨道沿轴系示意图(a，b)[26, 28]；PbTe中由温度导致的L价带和Σ价带简并及其布里渊区示意图(c，d)[12]Fig.3 Schematic diagram of orbital engineering to realize three-fold degenerate p orbitals in CaAl2Si2-type Zintl compounds and p orbitals of anions along principal axises (a, b)[26, 28]; schematic diagram of the temperature-induced band convergence of L and Σ bands in PbTe and corresponding Brillouin zone (c, d)[12]

在PbTe及其衍生化合物中，s-p轨道相互作用和spin-orbital相互作用在很大程度上决定了它们的能带结构[48-50]，因此，PbTe的轨道简并调控通常也从这方面入手。一方面，通过在PbTe基体固溶阳离子参与Te成键，从而对基体的Pbs—Tep的键进行扰动，可调控第一价带与第二价带的能量差，具备该效果的合金化合物有MTe(M=Mg[51]，Cd[52]，Mn[53]，Eu[54]，Yb[55]，Sr[56])等。另一方面，应变作用(包括外部应力、热膨胀、合金化等)也可以显著改变PbTe的能带结构[57]。例如，随着温度的升高，L带向下偏移而Σ带基本保持不变[46, 47]。而利用Se部分替代Te引起晶格收缩并引入负应变，可部分补偿热膨胀对L带的影响[12]。类似的能谷简并效应提升热电性能同样可以在SnTe[58-61]、CoSb3[13]、SnSe[62]、half-Heusler[17]等材料中发现。

3.2 共振能级

常规掺杂半导体中的施主能级一般位于导带底之下的禁带中(如P掺杂的Si半导体)，距离导带底的能量为ED。通常情况下，ED的能量很小，施主P可在热激发的作用下释放非共用的第5个电子到基体的导带中参与电输运。

与之相反的是，有些掺杂剂的施主能级位于导带之中(此时ED为负)，在能量上与基体的扩展态电子有所重叠，并与之发生相互作用，也即所谓的共振态能级。共振的过程可简易表达如下：由于施主的共振能级与基体的某一扩展态能级具有相同的能量，它们将发生共振并随之产生2个能量稍有不同的扩展态；随后，这2个由共振产生的扩展态又与其他扩展态具有相同的能量，因此继续发生上述共振过程；最终，共振能级发展成一个能量位置为ED、宽度为Γ的扩展能态[63]。此时，态密度在ED附近产生一个半高宽为Γ的洛伦兹峰，如图2b所示，极大地增强了电子态密度对能量的依赖关系。当费米能级位于ED附近时，将对塞贝克导率与塞贝克系数产生巨大影响。因此，在共振能级调控态密度的策略中，ED、Γ、EF是优化热电材料电学性能的关键调控参数。

在实际热电材料性能的优化中，需要仔细平衡上述3个参数之间的关系。已有报道表明，在Tl掺杂的PbTe[64, 65]、Al掺杂的PbSe[66]、Sn掺杂的Bi2Te3[67]等化合物中，共振能级均对其热电性能起到了积极正面的促进作用。其他一些过渡金属，如Ti[68]，Cr[69]，Sc[70]，In[71-76]也能在IV-VI族化合物的导带中产生共振能级。值得注意的是，共振能级在提升塞贝克系数的同时也会对载流子造成散射而降低电导率[71]，因此，共振能级是否对热电性能起到正面作用需要考虑塞贝克系数提升和电导率降低之间的平衡。有关共振能级对热电输运性质影响的更多细节可参考Heremans等的综述[63]。

3.3 离子输运

除了电子之外，带电离子也是热与电的载体。从线性响应理论中可以看出，带电离子的输运过程和电子的输运过程是十分类似的[77]。上文已讨论了电子的输运：能带简并的目的是提高电导率与塞贝克导率，而共振能级的目的是提高塞贝克导率与塞贝克系数。对离子输运而言，离子扩散系数对应于电导率，离子热扩散系数对应于塞贝克导率，它们之间的比值为索瑞(Soret)系数，对应于塞贝克系数[78]。引入离子作为承载热电转换的载体，相当于引入了额外的态，同时利用阳离子与阴离子热扩散速率的不同，也能使净熵流密度得到提高。这两点与能带简并、共振能级的思路是不谋而合的。

近期，有研究以K3Fe(CN)6/K4Fe(CN)6水性电解质作为研究对象，发现索瑞效应主要与Fe(CN)63-/Fe(CN)64-之间的熵变有关，而关键在于提高它们之间的离子浓度差。人为增大浓度差可以大大增强索瑞系数(4.2 mV/K)[79]。此外，也有研究在明胶体系中将Fe(CN)64-/Fe(CN)63-离子的氧化还原熵与KCl的离子扩散熵结合，获得了极高的热电势，使准固态离子型热电转换器件在准连续热充电/放电的工作模式下，利用人体温差实现了高达2.2 V的输出电压和5 μW最大输出功率[80]。离子输运的研究进展可谓是在“Go beyond Seebeck effect”上迈出了一步[81]。

4 电子速度调控

类似态密度调控策略，电子群速度的调控也可以从改变其绝对值与改变其形状2个方面进行描述。增加群速度有利于获得更高的电导率与塞贝克导率，而改变群速度的能量或动量依赖则对塞贝克系数有很大的影响，如图4所示。

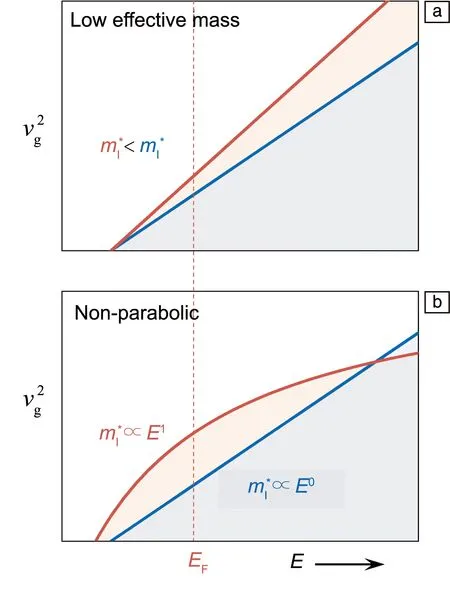
图4 在有效质量变化(a)和能带形状变化(b)影响下的电子群速度(vg)与能量依赖关系示意图Fig.4 Energy dependence of group velocity (vg) affected by inertial mass (a) and non-parabolicity (b)， respectively

4.1 低有效质量

通常来说，当直接带隙半导体的带隙不断减小时，由于导带和价带之间的相互作用，能带的色散关系将逐渐偏离抛物线型假设，色散的曲率将随电子能量变化发生改变，此时能带有效质量以及电子的群速度的能量依赖也将发生变化，如图4b所示。Kane[88]于1957年给出了非抛物线型能带的定量化描述：对导带而言，靠近带边的低能量电子具有很强的非抛物线型并服从类Dirac型色散，随着能量的升高，远离带边的高能电子逐渐恢复抛物线型色散。在这种描述下，能带边缘的有效质量很小且随着电子能量的升高而增大。

尽管Mg3Sb2-xBix化合物为间接带隙材料，能带结构变化导致有效质量变化对其热电性能的影响也十分显著。图5a为Mg3Sb2、Mg3SbBi和Mg3Bi2的理论计算能带结构图[89]，它们的导带极值点(conduction band minimum，CBM)均位于布里渊区中L-M方向，具有Nv=6的能带简并度。随Bi含量的增加，Mg3Sb2-xBix的带隙减小。实验测得的光学带隙变化趋势与理论计算结果也比较一致[90, 91](图5b)。此外，其有效质量也不断减小。图5c为利用Lyden方法[92]测试得到的惯性有效质量，可以看到，惯性有效质量随着Bi含量的增加而明显下降，从而导致了其迁移率的显著提升(图5d)[23, 93-99]。值得一提的是，Mg3Sb2-xBix最高的功率因子出现在x=0.5～1.5范围之间，而非有效质量最小的Mg3Bi2中，这是由于过高含量的Bi导致的小带隙会使得双极扩散效应更易发生，从而恶化其热电性能[89]。

图5 Mg3Sb2，Mg3SbBi和Mg3Bi2的理论计算能带结构(a)[89]；室温下n型Mg3Sb2-xBix合金的带隙Eg(b)[90, 91]；室温下n型Mg3Sb2-xBix惯性有效质量和Hall迁移率mH(d)随组分Bi含量变化的变化趋势[23, 93-99]Fig.5 Calculated band structures for Mg3Sb2，Mg3SbBi and Mg3Bi2 (a)[89]； the composition dependent band gap Eg of n-type Mg3Sb2-xBix (b)[90, 91]； inertial mass (c) as well as Hall mobility mH (d) for n-type Mg3Sb2-xBix at room temperature[23, 93-99]

4.2 能带各向异性

能带各向异性对热电性能的影响可从两方面来理解：一方面，能带各向异性的增强可以看成是布里渊区中的费米面沿某一方向延长，该方向有效质量减小，而另一方向的有效质量增大，载流子会优先沿着有效质量更小的方向运动，获得更高的迁移率，从而获得该方向上更优异的电性能。p型Mg3Sb2价带顶点位于布里渊区中的Γ点，具有明显的各向异性，能带沿Γ-K和Γ-M两方向的有效质量几乎一样，但远大于沿Γ-A方向的有效质量(K>8)[26, 104, 105]。研究人员发现，p型Mg3Sb2单晶沿轻带方向的载流子迁移率比沿重带方向的要高3倍，而它们的塞贝克系数相似，因此获得了更高的热电性能[104]。另一方面，强能带各向异性使费米面变成“针状”或“盘状”，可在三维块体材料中实现“低维”输运特性[106, 107]，它对于三维材料塞贝克系数的增强原理类似于二维超晶格[108]或一维纳米线[109]中的增强原理。有观点认为[110, 111]，对于晶体结构为面心立方的PbTe，能带结构的强各向异性(K≈8)是该材料高热电性能的主要原因之一。

5 弛豫时间调控

图6 不同散射机制下弛豫时间与能量依赖关系：(a)声学声子散射，(b)光学声子散射，(c)离化杂质散射Fig.6 Energy dependence of relaxation time when dominant scattering mechanism is acoustic phonon scattering (a), optical phonon scattering (b) and ionized impurity scattering (c), respectively

一方面，高性能热电材料需要载流子的输运过程尽可能顺畅，以保证较大的电流和熵流，即热电材料要求载流子的散射强度越弱越好，使电导率与塞贝克导率获得同步提高而保持塞贝克系数不变。另一方面，减小费米面之上高能载流子散射强度的同时增大费米面之下低能载流子的散射强度，可在单位温度场下获得更高的净熵流密度，在尽可能保证电导率的前提下提高塞贝克导率与塞贝克系数。针对上述两个层面，本节重点讨论电子散射过程的设计与调控方法。

5.1 声学声子散射

热扰动迫使原子偏移了其格点位置并对晶格周期性势场产生微扰，使得处于势场中的电子通过吸收/发射声子改变自身动量k并引起散射。因此，电子-声子相互作用是决定电子散射过程的重要机制之一。声学声子和光学声子在频率和色散关系上具有显著差异，它们对载流子的散射作用也不相同。半导体晶格中对载流子起主要散射作用的通常为频率较低的声学声子。

形变势是描述电子-声子(尤其是声学声子)相互作用的一个重要参数，它描述了材料中电子的某一能级(比如价带顶和导带底)相对于体积形变(应变)的变化关系[112, 114]。由于构成能带结构的原子轨道成分不同，当温度变化扰动化学键长时，不同电子能级对热应变的响应程度也是不同的。例如，IV-VI族化合物PbSe导带底的形变势约为25 eV，而价带顶的形变势约为35 eV[115]。因此，PbSe的导带电子具有较高的平均弛豫时间及电子迁移率，使得n型PbSe相较于p型能在较小的态密度下获得优异的热电性能[115]。类似的因声学声子对电子散射弱而导致的较高迁移率及性能，也在MgAgSb[116]、Ga掺杂的n型PbTe[117, 118]、BiCuSeO[119]等材料中被发现。

5.2 其他散射机制

在多晶材料中，电子的散射过程常常伴随着除了本征的声学声子散射之外的其他散射机制。例如，当经历了复杂的制备、掺杂、固溶工艺后，材料内部的微观结构越来越复杂，所引入的晶格缺陷对电子的散射作用也越来越显著，降低了载流子的迁移率，使得材料低温下载流子迁移率偏离声学声子散射的温度依赖关系μH∝T-1.5。热电材料中调节载流子浓度的传统手段通常是异价原子掺杂，当掺杂浓度较高时，这种方式在有效调节载流子浓度的同时，也会对电子造成一定程度的散射[120]，因此，寻找高效的掺杂剂或利用材料本身的空位等缺陷实现载流子的有效调控有利于减少对电子的额外散射。近期，有研究通过在Cu3SbSe4中固溶少量的CuAlSe2降低Sb空位的形成能，稳定材料中的大量阳离子空位，在实现载流子浓度提升的同时，维持了该材料本身的载流子迁移率[121]。

除点缺陷外，在含有高浓度晶内位错的PbSe、PbTe以及它们的化合物中[83, 122, 123]，由于位错浓度极高，引入的位错缺陷不仅散射声子，实现了晶格热导率的降低，同时对载流子也造成了一定程度的散射，使得载流子迁移率降低。在离子晶体中，位错的悬挂键容易捕获电子从而形成库伦电势场，展现出类似离化杂质散射的散射过程[124, 125]，此时t=1/2、s=0、r=3/2，载流子迁移率的温度依赖关系呈现出μH∝T1.5，而这一效应在较低温度(室温附近及以下)时尤为明显。Mg基化合物Mg3Sb2合金在较低温度时也常出现类似的迁移率-温度依赖关系，其额外的散射往往来源于材料中大量的带电晶界[126, 127]。这是由于该材料的晶粒尺寸、氧化程度与制备工艺密切相关，制备工艺的不同会导致材料的载流子迁移率发生巨大变化[96-98, 128]。如图7a所示，当材料的烧结温度较低时，该材料晶粒尺寸过细，晶界散射明显；提升材料的烧结温度可以有效增大材料的晶粒尺寸，减弱晶界散射，提升材料室温附近的载流子迁移率及热电性能[127]。此外，在制备过程中采用钽管密封或大颗粒热压也可以防止材料氧化和大晶粒尺寸形成[19, 98]，从而使材料获得高热电性能。

图6(c)为自动相位搜索算法估计的补偿相位与准确相位Δφj(n)之间的差值曲线图，相位差值以0为中心上下浮动且浮动范围在[-0.01,0.015]内，即在每个n时刻估计相位与准确相位的误差都不超过0.015.可见对于传统散射波干扰，搜索算法估计补偿相位的精度较高，从而具有较好的干扰对消效果.

half-Heusler的有效质量比传统热电材料高很多，通常需要掺杂/固溶大量的合金元素优化该材料载流子浓度[5]，从而实现其热电性能的提升，因此，研究人员通常认为其载流子的主导散射机制为合金散射[129]，迁移率应随载流子浓度(合金含量)的提高而单调下降。然而，合金散射机制无法完全解释实验结果。大量实验结果表明，half-Heusler合金的迁移率随载流子浓度增加呈现先上升后下降的变化趋势，如图7b所示[14, 129-132]。近年来有研究指出，p型FeNbSb在300～1000 K温区内的载流子主导散射机制为光学声子散射[133]，增加载流子浓度能够提高屏蔽效应从而提高迁移率。相关研究进一步发现这种屏蔽效应来源于纵-横光学支劈裂(LO-TO splitting)[130]：在ZrNiSn体系中，LO-TO splitting会随着载流子浓度的增加而减小。这种现象说明化学掺杂效应会在材料中带来屏蔽效应，并减弱其极化电场，从而减弱了相应极化光学声子散射。与此同时，载流子浓度的增加会强化合金散射。两种效果的叠加致使half-Heusler热电材料中的迁移率表现出先增加后减小的非线性现象(图7c)[130]。而拐点正好对应着其热电性能的最优载流子浓度。

5.3 能量过滤效应

若在电子的传输路径上设置势垒，电子波包在产生反射波的同时也会产生透射波，即量子隧穿效应：在势垒中波函数不为0，也有发现粒子的概率[134, 135]。入射的电子能量越高，则有更多的透射，更少的反射。当然，如果入射电子能量超过势垒，也会存在反射波。这是能量过滤效应的核心基础。

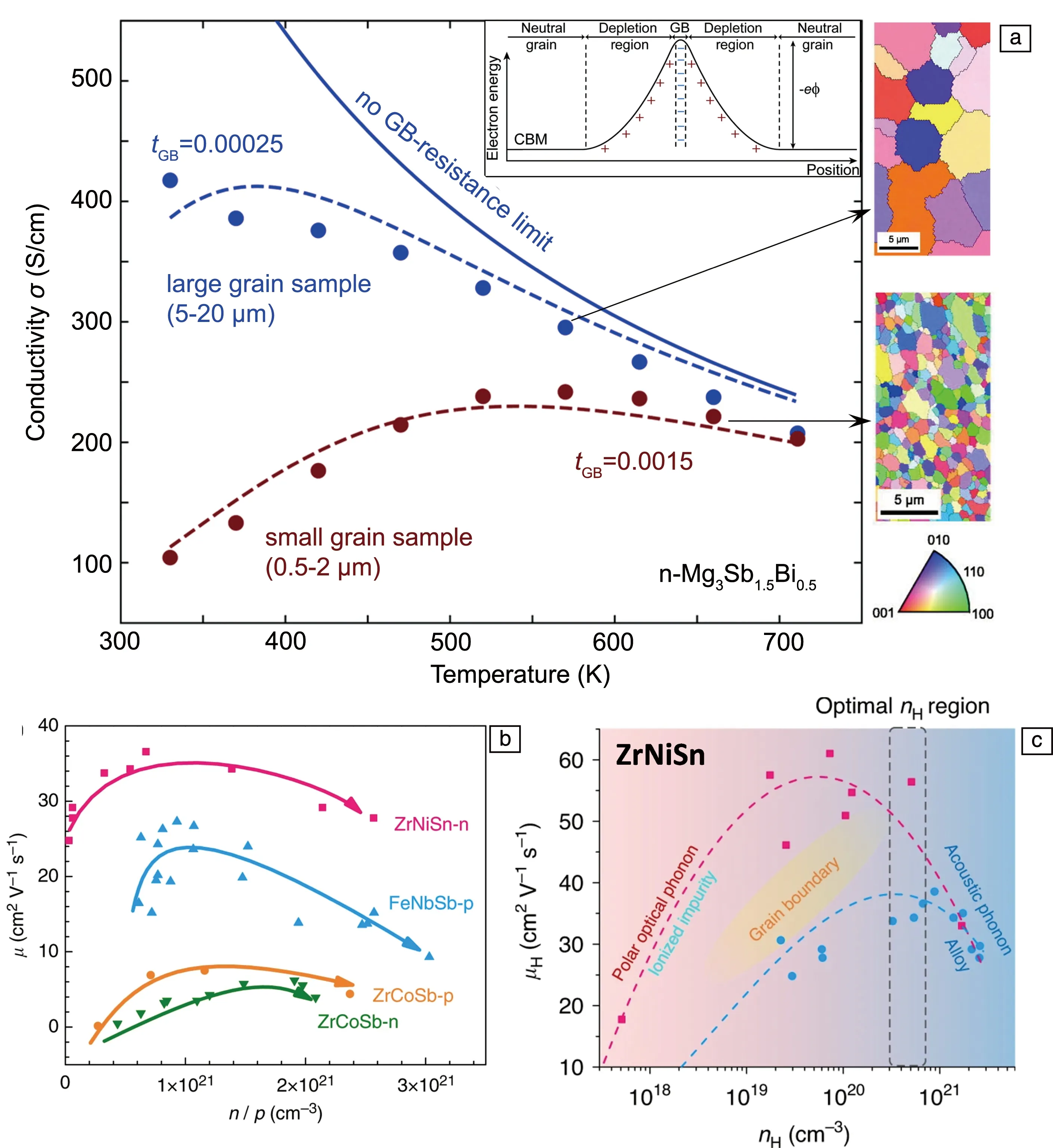
图7 n型Mg3Sb1.5Bi0.5不同晶粒尺寸时的电导率[127]，其中曲线为模型结果，与实验值符合较好(a)[126]；几种half-Heusler材料的迁移率随载流子浓度变化的关系(b)[14, 129-132]；300 K下单晶(红色数据)和多晶(蓝色数据)ZrNiSn的迁移率随载流子浓度变化的关系(c)[130]Fig.7 Electrical conductivity of n-type Mg3Sb1.5Bi0.5 with different grain sizes[127], both of which are well described by the model (curves) (a)[126]; carrier concentration dependent carrier mobility for several half-Heusler compounds (b)[14, 129-132]; carrier concentration dependent carrier mobility for single-crystalline (red data) and polycrystalline (blue data) ZrNiSn at 300 K (c)[130]

能量过滤效应增加了电子散射过程的能量选择性，使得低能电子相较于高能电子而言更容易被散射，形式上表现为散射因子r的增加。该效应可以显著提高塞贝克系数，但与此同时也会降低电导率。当前者的正面贡献大于后者的负面贡献时，引入能量过滤效应可以有效地提高热电材料的性能[136]。而其中的关键，在于势垒的调控。

针对界面势垒的调控问题，近期有研究提出体现能量过滤优势效应的关键参数是“界面塞贝克系数”。基于有效介质理论，Lin等[137]建立了非均质“复合材料”的串联模型，并对能量过滤作用下的声电子输运进行分析。该研究以n型Mg3Sb2及它与石墨烯的复合材料为例，研究发现：晶相和晶界相在电学性能上有着本质不同，而能量过滤效应主要集中于晶界相中，带来晶界相的“界面塞贝克系数”的显著提升。因此，提高“界面塞贝克系数”在整体塞贝克系数中的比重是材料热电性能突破的关键。通过复合石墨烯优化界面热阻，可显著提高晶界相的温度梯度占整体材料温度梯度的比重，带来材料整体塞贝克系数和功率因子的提升。最终，n型Mg3Sb2的峰值热电性能提高了40%。

能量过滤效应也适用于有机-无机复合热电材料。通过有机热电材料与无机纳米材料(如碳纳米管、石墨烯、纳米无机热电材料)之间的电荷转移，可以构建出能够过滤低能载流子的界面势垒[138]。除此之外，在热电薄膜材料表面引入表面势垒，同样可以实现类似的能量过滤效应，这也是对薄膜热电材料性能进行调控的常用手段之一[139]。有关能量过滤效应对热电输运性质影响的更多的细节，可参考Amouyal等的综述[140]。

6 优异热电材料基本特征

热电材料研究中的首要目标通常是找到具有高热电优值的新材料或是提升现有材料的热电优值。以此为目标，研究者们基于物理模型并结合实验结果验证，总结出了优异热电材料需要具备的基本特性，并发展了一些可以直接判断热电材料功率因子或热电优值高低的参量。

6.1 加权迁移率和品质因子

(4)

加权迁移率是与载流子浓度无关的参量，它表明一个材料在载流子浓度优化以后，可以实现的最高功率因子。而材料优化后能实现的最大热电优值则取决于品质因子B。品质因子是由Chasmar和Stratton在1959年最早提出[141]，其正比于加权迁移率，反比于晶格热导率：B∝(μW/κL)。品质因子越大，热电材料经过载流子浓度优化后能实现的最高热电优值也越大。

6.2 电输运模型的简化和发展

经过上文讨论，可以得知，从物理图像的角度看，功率因子是材料能带结构、散射机制和费米能级对电子输运过程的反映；而从数学层面上来说，功率因子是一系列参量的集合，包含了能带简并度[12]、能带有效质量[82]、载流子散射因子[15]、简约费米能级[15]及弹性常数[46]等，这些参量成为衡量某材料功率因子高低或调控功率因子的指标。显然，单一的某参量并不足以直接判断功率因子的高低，并且实验上这些参量需要通过Hall测试以及大量复杂的运算才能获得，以某一单一参量作为指标来指导材料开发或优化的效率较低。这导致传统的热电材料研究往往需要进行不断的重复实验，包括材料制备、结构表征、输运性能测试，也包括部分通过模型/计算预测热电材料在不同温度下的优化点。为了更高效地进行热电材料研究，近期，有许多工作聚焦于输运模型的简化。

近期，有研究总结了电学品质因子BE[22]。电学品质因子包含了决定功率因子的参量中与能带结构相关的所有参量，可以直接作为判断热电材料优化后功率因子高低的指标：

(5)

与加权迁移率相比，电学品质因子是与温度无关的参量。实验上，可从测试的功率因子直接求解电学品质因子：

(6)

其中，Fj为费米积分：

(7)

其中，ξ是约化能量，即E/(kBT)；η是简约费米能级，即EF/(kBT)。然而，使用常规的输运模型求解电学品质因子需要求解费米积分，较为复杂。将强简并极限和非简并极限下的严格解析解用Sigmoid函数平滑拟合[142]，如图8a所示[22]，所得曲线与严格费米积分计算得到的结果之间的误差在3%以内，且其解析表达式仅包含初等函数，计算方法非常简单。因此，可以用该方法来替代复杂的费米积分，那么材料的电学品质因子可以由式(8)计算获得：

(8)

其中，Sr=|S|/(kB/e)，可被称为约化塞贝克系数。

电学品质因子可以通过非常简便的方法得到。对于一个给定的样品(无需载流子浓度优化)，只需要获得该样品在任意温度下的任意一组塞贝克系数和电阻率，即可获得该材料的电学品质因子。对于理想的热电材料而言，电学品质因子是与温度无关的参量，也就是说，如果电学品质因子随着温度的改变而发生变化，意味着此时材料中存在着其他的物理现象，例如能带汇聚、额外的电子散射以及双极扩散效应，如图8b所示[22]。这使得电学品质因子成为一种方便实用的，对指导热电材料的优化有着实际应用意义的电学输运参量。

也有研究人员对加权迁移率作了类似处理，使用简单的初等函数来计算加权迁移率[143]：

图8 利用Sigmoid函数对强简并极限与非简并极限下的约化功率因子进行拟合(a)；能带汇聚、额外散射机制、高温下双极扩散效应对电学品质因子随温度变化影响示意图(b)[22]Fig.8 The Sigmoid selection function (denominators of the fractions in the sum) smoothly interpolates between the analytic degenerate and nondegenerate limits (numerators of the fractions in the sum) (a); a model system involving a convergence of two identical bands, additional charge scattering, and a bipolar conduction (b)[22]

(9)

这里，h为普朗克常数，me为电子质量。

上文提到，在SPB-APS假设下，加权迁移率随着温度变化关系为T-3/2，而电学品质因子则不随温度变化而变化。图9为两者之间的清晰对比。n型PbTe的主导散射机制为声学声子散射，其加权迁移率随温度升高呈T-3/2下降[143]，如图9a所示。而n型PbTe的有效质量、弹性常数等决定电学品质因子的物理参量的温度依赖性较弱，其电学品质因子基本不随温度的改变而发生变化[22]。n型Mg3Sb2合金的情况更为复杂，其晶粒尺寸与制备工艺密切相关，当晶粒尺寸很小时，晶界散射明显，使得该材料在室温附近的迁移率大幅下降，室温附近的电学品质因子急剧降低[98, 126-128, 143〗，如图9b所示。图9c和9d展示了散射变化分别对加权迁移率和电学品质因子的温度依赖关系的影响[22]。

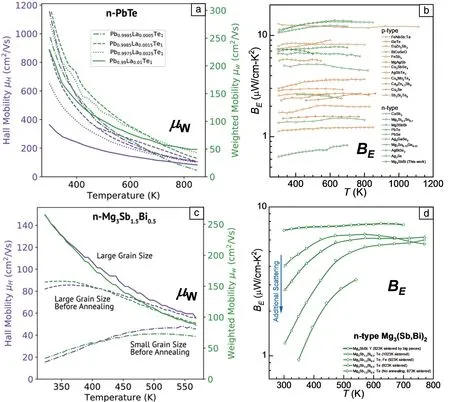
图9 n型PbTe和n型Mg3Sb1.5Bi0.5的Hall迁移率(μH)及加权迁移率(μW)随温度的变化(a，c)[143]；n型Mg3(Sb,Bi)2等多种材料的电学品质因子(BE)随温度的变化(b，d)[22, 98, 126-128, 143]Fig.9 Temperature dependent Hall mobility (μH) and weighted mobility (μW) for n-type PbTe and n-type Mg3Sb1.5Bi0.5 (a, c)[143]; temperature dependent electronic quality factor (BE) for materials including n-type Mg3(Sb,Bi)2, et al (b, d)[22, 98, 126-128, 143]

对于如何从实验测得的塞贝克系数和Hall载流子浓度计算材料的有效质量也有类似的简化处理[144]。此外，近期也有研究将载流子浓度中的费米积分部分2/π0.5F0.5(η)定义为约化载流子浓度nr，用以表达塞贝克系数、迁移率、洛伦兹常数等，以简化SPB模型中的计算[145]。尽管这些工作的简化思路和所用函数不尽相同，其主要目的都是简化输运模型中的费米积分部分，以方便模型在实际研究中的高效使用。这些工作都具有帮助理解材料输运性质、指导材料设计的实际意义。

7 结 语

热电技术研究是一种应用驱动型的基础研究，在多学科日益交叉融合的大背景下，新理论、新材料和新技术层出不穷，热电研究正步入新一轮的快速发展。许多高端应用环境(如5G通讯、芯片级发电/制冷、量子计算、物联网、深空探索等)在小型化、可持续、极端应用条件等方面提出了严苛的要求，这也对热电技术的理论研究、材料研究、器件研究提出了新的挑战。

随着研究的深入，人们越来越意识到传统电输运理论框架的局限性：当出现自旋轨道耦合诱导拓扑效应，电子强关联打破单粒子图像以及强磁场条件突破玻尔兹曼输运时，如何精准地描述电子的输运过程并总结归纳出具有针对性的调控策略成为下一阶段热电材料电输运调控的重要研究方向之一。本综述介绍了热电材料中基本的电子输运机制以及提升材料热电性能的调控方法，大量的理论和实验研究卓有成效。然而，理论框架的突破意味着研究者们需要重新审视热电材料中的电输运过程，或从更宏观的统计角度，或从更微观的多体相互作用角度，未来将会发展一系列极具特色的热电材料性能调控策略，热电技术将迎来新一轮的蓬勃发展。