热电性能测量方法

郑 欣，韩 屾，高梓恒，付晨光，朱铁军

(浙江大学材料科学与工程学院 硅材料国家重点实验室，浙江 杭州 310027)

1 前 言

能够实现热能和电能直接转换的热电材料因体积小、寿命长、全固态、易维护等优点近年来引起了广泛的关注和研究。目前已经成功实现了多领域的商业化应用，并在深空发电、精准控温方面具有不可替代的优势。无论是温差发电器件还是固态制冷器件，最大转换效率ηmax均与材料的热电优值zT直接相关，其具体表达式为zT=S2σT/κ，式中S为Seebeck系数，σ为电导率，κ为热导率，T为温度，实际研究中常用zT值来衡量材料热电性能的优劣。为了提高热电器件的转换效率，寻找具有高zT值潜力的材料体系，并通过组合手段进行性能优化已成为了热电领域的重要研究方向。

zT值的测量方法主要有2种。Harman法[1-3]基于通电时热电材料中的Peltier效应和Seebeck效应，在真空绝热条件下测量并分离出欧姆电压UO和塞贝克电压US，利用公式zT=US/UO计算可以直接获得材料的zT值，该方法简单快速，但受限于寄生热效应等因素的干扰，测量结果的精确程度和可重复性均有不足，因此该方法现阶段仅常用于工业上快速筛选材料[2]。实际研究中，更为普遍获取zT值的手段是分别测量材料的Seebeck系数、电导率以及热导率，再根据定义式计算得到zT值，且这些参数的测量有助于研究人员更好地理解材料的热电输运性能。

热电材料的开发研究中，通常需要参考已公开发表的材料数据总结规律，结合实验探究机理并调控材料性能，而不同研究团队使用的测量手段、表征设备及操作方法不同造成的数据偏差较大，不利于数据的对比分析。此外，报道性能优异的热电材料研究结果时，数据的准确性与可重复性极其重要。因此，准确对各输运参数进行表征并得到可靠的zT值是进一步探索热电材料性能提升手段的必要前提。

自2009年起，国际能源署(international energy agency, IEA)基于《先进材料输运性能实施协议》(implementing agreement for advanced materials for transportation)，以室温区商用的Bi2Te3合金为标准样品，在世界范围内7家热电技术研究单位开展了巡回实验，对同一样品进行Seebeck系数、电导率、热扩散系数、热容参数的重复测试，最终对比发现，这4项热电参数的测量精确度分别约为±4%、±9%、±6%和±15%[4, 5]，仅考虑这些误差的简单叠加就会使zT值误差超过20%，对样品性能的判断造成极大影响。除了测量原理决定的系统误差外，测量设备和人工操作也会带来一定的误差。随着本领域研究的发展，商业化表征设备的推广普及一定程度上减少了各个研究团队自制设备带来的测量差异，并且相同测量温区的测试原理基本一致，基于这一发展背景，如果能给出一定的操作规范，并且在保证精度的同时更多地关注测量结果的合理性和可重复性，便可有效地避免实验误差，获得高质量的数据结果，方便不同研究团队之间进行研究成果的对比分析。

本文将针对几个关键热电参数的表征方法及测量原理展开概述，重点介绍测量不同热电参数时的误差来源、操作要点及注意事项，旨在帮助热电领域的初学者以及相关操作人员减少一些可以规避的测量误差，获得可信的数据支撑研究分析，推动热电材料的性能优化研究取得更大进展。

2 室温以上电输运性能测试

2.1 Seebeck系数

样品两端电势差与温差之比即为Seebeck系数，测量系统中热电偶直接测得的通常是样品与热电偶的相对Seebeck系数Srel，表达式为Srel=ΔV/ΔT，测量时应尽量保证温度和电压在同一点处测得,回路中的热电接触电阻尽可能小，规定以两热电偶间平均温度T0=(T2+T1)/2为样品实际温度。

热电偶常见的接触方式有两点式(图1a)、单轴四点式(图1b)和离轴四点式(图1c)。两点式中热电偶嵌入加热器中且不与样品直接接触，温度和电压无法在同点测得，测量精度低；单轴四点式中热电偶同样嵌入加热器，可与样品以恒定的压力直接接触，冷热指效应小且热接触电阻较低[6]，但因为测量样品薄、横截面积大，尤其是在样品热导率大的情况下，样品-加热器与样品-热电偶两界面温差差异较大，难以保持样品温度均匀恒定，从而引入测量误差；离轴四点式可以同时测得样品的Seebeck系数和电导率，热电偶与样品直接接触，消除了样品与加热器/散热器之间的热接触电阻，但因为冷指效应的存在可能使测得的温度和温差偏小，最终导致获得的Seebeck系数偏大。目前商用的测量仪器大部分采用离轴四点式。

由Seebeck系数定义式可知，理想情况下，平均温度一定时，ΔV-ΔT关系应该是一条过原点的直线，但在实际情况中由于热电偶状态、热电接触情况和样品本身性质等多种因素的影响，会使该直线在纵轴上产生截距，通常称该截距大小为偏移电压offset(见图1d和1e)。考虑到实际误差的存在，相应的数据处理方式主要分为点除法和斜率法2种。

点除法直接将测试点与原点所连直线的斜率作为测得的相对Seebeck系数，如图1d所示。但实际上存在偏移电压后，ΔV-ΔT关系应由式(1)描述：

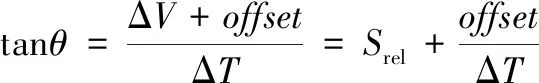
(1)

从式(1)中可以看出，计算得到的斜率tanθ并非理想的相对Seebeck系数值，需要加以校正。商用设备的配套测试程序提供了热电偶温度的人工校正通道，但偏移电压的大小同时也与温度相关，室温下校正良好并不意味着高温区测试的准确性能够得以保持。通常情况下，温差越大因存在偏移电压而引入的误差越小，但由于仪器条件限制、热对流以及样品热传导等因素使得大温差的建立较困难，可能会使得到的ΔV-ΔT数据点偏离线性关系，且当测试平均温度相对较高时，受限于设备腔体温度的整体上升，大温差的构建将更加困难，故点除法的理想测试温差范围应在3～5 K之间[7]。

不难看出，偏移电压的引入只改变了ΔV-ΔT直线的截距,而不改变其斜率大小，即理想情况下的相对Seebeck系数，在T0温度下改变施加的温差，测得直线上多组ΔV-ΔT关系就可以求得其斜率，得到更接近理想情况的相对Seebeck系数，如图1e所示。图1f对Nb0.8Ti0.2FeSb样品在300～1100 K温度范围内分别利用点除法和斜率法处理得到的Seebeck系数结果进行了对比，从图中可以看出，通过点除法得到的Seebeck系数准确性较低且数据点较为弥散，而通过斜率法得到的曲线更加平滑，有利于改进测量结果，获得更加准确的实验数据。

使用斜率法时，与小温差变化范围(见图1g两蓝线所夹区域)相比，在较大的温差变化范围(见图1g两红线所夹区域)内进行取值更有利于减小线性拟合结果与真实结果的偏离程度。图1h为不同温差跨度下Nb0.8Ti0.2FeSb样品Seebeck系数的测试结果，特别对比了结果相差较大时ΔV-ΔT的实际测试分布点，发现在较大的温差跨度下测得的Seebeck系数波动范围更小且得到的Seebeck系数值更接近样品真实值。此外，通常还会在同一温差下进行多次电势差测量取平均值以减小偶然误差。

热电偶作为测试过程中最有可能引入系统误差的部分，其状态会直接影响测得的Seebeck系数准确性，因此需要注意以下几点：① 系统测得的Seebeck系数通常是样品与热电偶的相对Seebeck系数Srel，需要从其中扣除热电偶的Seebeck系数Swire才能获得样品的绝对Seebeck系数Sabs，即Sabs=Srel-Swire。② 测量易反应、易挥发的样品后应及时清洁热电偶，定期用标样检验热电偶老化状态并及时进行更换。图1i为分别使用新旧热电偶测得的Ba0.08La0.05Yb0.04Co4Sb12样品电性能数据，Seebeck系数S的偏差在800 K左右约达10%，体现在功率因子PF值上可能会造成更大的偏差[7]。③ 保证良好的热电接触。采用离轴四点式的商用仪器通常需人工调控热电偶与样品间的接触，适当增大热电偶与样品间的压力可以减小接触电阻及热阻，但压力过大可能会使样品移动、弯曲甚至断裂。理想热电接触下，S-T曲线以及ΔV-ΔT曲线应不随加热速率、温差大小、气压变化而变化，因此可以通过曲线的迟滞情况和可重复性检验热电接触是否良好[6, 8]。实际测量中，通常选择导热能力更强的氦气作为保护气氛以改善热接触[9]。

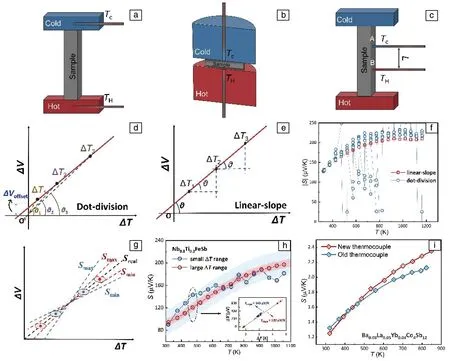
图1 测量Seebeck系数的3种热电偶接触方式：(a)两点式，(b)单轴四点式，(c)离轴四点式；2种Seebeck系数测量数据处理方式：(d)点除法，(e)斜率法；Nb0.8Ti0.2FeSb样品使用斜率法与点除法获得的Seebeck系数对比(f)；使用斜率法时温差范围对测量误差的影响(g)；不同温差范围下使用斜率法测试Seebeck系数的对比(h)；新旧热电偶对Seebeck系数测量的影响(i)Fig.1 Three common thermocouple contact geometries for measuring Seebeck coefficient: (a) 2-point type, (b) uniaxial 4-point, (c) off-axis 4-point; two processing methods of Seebeck coefficient measurement data: (d) dot-division, (e) linear-slope; comparison of Seebeck coefficients obtained by linear-slope method and dot-division method for Nb0.8Ti0.2FeSb sample (f); effect of ΔT range on measurement error when using linear-slope method (g); comparison of Seebeck coefficient measured by slope method under different ΔT ranges (h); the effect of using new and dirty thermocouples on Seebeck cofficient measurement (i)

2.2 电导率

半导体热电材料电导率的测量方法主要分为范德堡法[10]和四点法。其中范德堡法对样品形状因子没有严格要求，常用于测量厚度均匀、无孔洞的扁平状样品的电导率，测量原理示意图如图2a所示，依次在相邻两接触点间通电流，测量另外两接触点处的电压，根据欧姆定律分别计算出电阻值R，将读数两两组合后可求得样品的电阻率，计算原理如式(2)所示：

(2)

式中，σ是测得的样品电阻率，d是样品厚度，f是考虑到样品并非理想二维材料而引入的修正函数。需要注意的是，范德堡法测量电导率对接触点的质量极其敏感，故要求位于样品边缘的4个触点要尽可能小。此外，将范德堡法与磁场结合，改变电流电压触点还可以测量样品的霍尔系数，详细内容将在室温以下电性能测试的部分进行介绍。

对于块体热电材料，通常采用四点法测量其电导率，测试原理如图2b所示。以商用LSR-3为例，已知探针间距L和样品横截面积A，向回路中通一定大小的电流I，通过两热电偶探针测得E、F触点间的电势差ΔV，即可求得样品电导率σ=IL/(ΔVA)。从表达式中不难看出，仪器给出的电导率数值不仅与样品本身电性能有关，还与探针间距L和样品横截面积A有关，一些商用仪器测量前不会自动校准探针距离，长时间运行后，由于热膨胀或老化，热电偶间距会偏离所设定的默认值，故每次测试前要准确测量探针间距。四点法测电导率中，样品的形状因子非常重要，被测的条状或棒状样品应尽量保证尺寸均匀，样品长度与探针间距之差应大于2倍样品厚度，以确保探针之间的测试区域内电场线相互平行且均匀分布。

需要强调的是，电导率测试过程中直接读取的参数是两探针间的电压，因不同样品导电性能存在差异，应合理选择测试电流的大小以实现电压表的准确读数，避免出现样品电导率过低导致电压信号超出量程，或样品电导率过高导致电压信号相较于量程太小的情况。以商用LSR-3为例，可以利用快速测试探针电阻选项显示热电偶两触点间测得的U-I特性曲线帮助选择合适的测试电流。理想情况下，U-I关系应该是斜率不变的一次函数，如果测得的图像偏离直线，说明电接触不良或样品电导率过低导致电压表测得的数值超过量程，此时应选择较小的测试电流以保证U-I关系线性良好以及测试的准确性。图2c展示了测试电流在0～100 mA范围内时不同导电特性样品的U-I特性曲线，其中电导率较高的VFe0.99Co0.01Sb样品呈现出良好的U-I线性关系，而未掺杂的TiCoSb样品由于样品电导率较低，已接近设备电压表量程上限，偏离线性。此外，需要考虑样品电导率随温度的变化，尽量在完整测量温度范围内保证电压信号的取值合理。

需要注意的是，商用仪器常利用四点法同时进行Seebeck系数和电导率的测试，Seebeck系数的测量需要构建温差，此时会产生只与温差方向有关而与电流方向无关的Seebeck电压VS，而测量电导率需要通电流以产生与电流方向有关的欧姆电压VO，因此热电偶测得的电压包含了Seebeck电压和欧姆电压，常通过正反向各通一次相同大小的电流以消除Seebeck电压，计算原理如式(3)所示：

(3)

如图2d[11]，V1(>0)、V2(<0)分别为正向、反向通电流后探头测得的电压，利用其平均值可以得到最终电导率。但通电一段时间后Peltier效应的存在又会引入另一附加电压，此附加电压也与电流方向有关，因此无法通过电流反向消除。进行高精度电导率测量时，为保证数据准确性，电压点的测试应尽量迅速(通电/断电～1.3 s内)。

图2 测量电导率的2种常见方法：(a)范德堡法，(b)四点式；利用离轴四点式仪器测量不同电流下的U-I特性曲线(电压表量程为2500 mV，在LSR-3上进行)(c)；改变电流方向测量电压的大概变化情况(d)[11]Fig.2 Two common methods for measuring conductivity: (a) van der Pauw method, (b) the linear 4-point method; U-I curves under different measuring currents by off-axis 4-point method (voltmeter range is 2500 mV, operated on LSR-3) (c); change of measured voltage after changing the current direction (d)[11]

3 室温以上热输运性能测试

热电材料在室温及以上环境下的热导率通常很难直接测得，但可以通过分别测量热扩散系数D，密度ρ以及定压热容Cp后计算得出，相应的计算公式为：

κ=DρCp

(4)

其中，密度通常使用阿基米德法[2, 7]测得，对样品形状没有要求，但为避免液体进入样品孔隙造成测得的密度偏大，可以通过检验浸入液体前后样品的干重是否发生变化来排除此误差。接下来将介绍室温以上热扩散系数及定压热容的表征方法。

3.1 热扩散系数

激光闪射法[12-14]常用于测量材料热扩散系数随温度的变化， 激光热导分析仪(如LFA-457)就是采用该方法测量热学性能。测试原理如图3a所示，激光源发射高能脉冲激光束(见图3b)对样品下表面进行短时间辐照，该激光能量被样品吸收后以热量的形式传导到上表面，用红外探测器记录上表面温度随时间的变化过程，从而得到相应的升温信号，通常热信号会先迅速增大至某一峰值，再缓慢减小。假设该过程是理想的一维热扩散、外界环境绝热无损耗、光脉冲宽度接近无限小，可推导出材料热扩散系数的计算公式：D=0.1388d2/t1/2，其中d为样品厚度，t1/2为被测样品表面温度达到峰值一半时所需的时间即半升温时间，如图3c所示。

图3 激光闪射法测试热扩散系数原理图(a),激光脉冲(b)与探测信号随时间变化(c)示意图，激光热导仪在不同样品厚度及探头缺乏液氮冷却情况下测得的信号曲线(d)Fig.3 Schematic diagram of thermal diffusivity measurement by laser flash apparatus (a), laser pulse (b) and change of detection signal with time (c); signal curves measured by laser thermal conductivity meter under different sample thickness and lack of liquid nitrogen (d)

为保证测量精度，被测样品须为大小合适、表面平行、厚度均匀的片状固体，样品直径或边长不宜太小，尺寸过小将偏离无限大平面、一维传热的理想假设，边界条件的影响将增大。对于不同导热能力的样品要选择合适的厚度，高热导率材料应较厚，以免传热时间过短，升温过程数据点不足；而低热导率材料应较薄，否则传热时间过长、热损耗明显，且引入信号漂移、环境变量等因素影响实验精度。如图3d所示，以热导率较低、直径为12.7 mm的Nb0.95Hf0.15CoSn圆片为例，样品厚度为1.2 mm时测得的信号正确、结果重复性好；但厚度为2 mm的样品信号曲线形状与标准差距较大，难以拟合得到准确的半升温时间。

选择合适的测量模型可以对测量过程产生的热损失及误差进行一定的修正，主要的修正模型有以下几种：Cowan模型[14]考虑了样品表面热损失以及方形激光脉冲校正；Clark和Taylor模型[13]对边界辐射热损失和脉冲宽度进行了研究校正；Cape-Lehman模型[12]在Cowan模型的基础上考虑了纵向热传输过程中的热损失，在实际测试中使用Cape-Lehman模型可以获得较为满意的结果。

为了增强样品表面对光辐射的吸收率和发射率，测试前要对样品上下表面进行石墨涂覆处理，但涂层厚度应均匀适宜，太厚会引起热量在石墨层上横向传输，甚至高温下石墨层可能翘起，导致热扩散系数测试结果偏低。测量过程要注意样品不得倾斜、尺寸应与支架匹配，以避免激光泄漏，还要定期检查传感器是否存在污染情况；测得的信号曲线形状有助于分析热扩散系数结果的准确性及产生的原因，如图3d中分别给出了样品厚度选择不适宜、冷却探头的液氮不足时的测量信号曲线，可借以监测测量过程中出现的异常数据点，分析异常点出现的可能原因。此外，激光热导分析仪系统可通过对比待测样品与已知热容的标准样品间的信号获得待测样品定压热容Cp。热电表征中获得热容的其他方法将在下文进行介绍。

3.2 定压热容

3.2.1 差示扫描量热法

差示扫描量热仪(differential scanning calorimeter，DSC)可以测量样品与标准参比物在程序设置温度下所需能差(功率补偿型)或温差(热流型)随温度和时间变化的关系[15]，从而得出样品的定压比热。直接利用公式cp=(dH/dT)/m即可得到升温速率与温度变化间关系：dH/dt=cpm(dT/dt)，但因为测量过程中校正系数变化、基线漂移、升温速率非线性变化等影响，此方法求得的定压热容误差较大而不可取，因此通常采用间接法获得较为准确的测量值。如图4a，先测量出空样品台的DSC曲线作为基线，再以同样的条件测出标样(蓝宝石)、待测试样的DSC曲线，两线相比由式(5)可求得待测样品的比热：

(5)

因样品挥发会污染仪器，导致基线不稳、测试精度降低，故使用时要注意仪器内部的清洁度。同时，标样的比热与样品的比热越接近越好。

3.2.2 杜隆-珀替法

杜隆-珀替(Dulong-Petit)将气体分子热容理论直接用于固体，发现晶体摩尔定容热容CV,m为与温度无关的定值，即CV,m=mcV=n3R J/mol，式中n为晶胞中原子个数，cV为定容比热，m为摩尔质量，R为摩尔气体常数。对于块状固体，定压升温过程中材料比体积变化很小，故常用杜隆-珀替法算得的定容比热代替公式中的定压比热进行热导计算。但实际上，定压比热会随温度发生改变。低温时，温度升高导致不同频率的声子被激发并对比热产生贡献，使得比热快速增大；温度继续升高至德拜温度附近，不再激发更高频率的声子，此时比热趋近于杜隆-珀替值；进一步升高温度，非简谐振动会造成晶体体积膨胀，比热随温度升高而继续缓慢增大，故高温下杜隆-珀替法算得的比热会小于实际定压比热，造成对材料热导的低估。因此一般认为，杜隆-珀替法获得的定压比热在德拜温度以上一定范围内才与实际值较吻合，在比热计算中应该尽可能考虑热膨胀项。

3.2.3 模型计算法

定压热容Cp可以分为简谐声子项Cph,H、热膨胀项CD和电子项Ce3部分的贡献[16]，即Cp=Cph,H+CD+Ce，高温下忽略电子贡献部分并采用德拜模型，可得定压热容的表达式为：

(6)

其中nm是单位质量的原子个数，kB是玻尔兹曼常量，BT是等温体模量，α是线膨胀系数，χ是比体积(即密度倒数)，θD是德拜温度，计算公式为：

(7)

h为普朗克常量，Vc和N为晶胞的体积及其包含的原子个数，因此，要计算定压比热还需测量样品的平均声速vs。

图4b为反射式时差法测量声速的原理图，已知样品厚度d，声速νs=2d/Δt。应注意用于声速测量的样品不能太薄，为区分两组连续的接收信号，样品厚度应为超声波波长的4倍以上。另外，信号不稳定、声波延迟、信号发射/接收器与样品接触不良以及人工读取波峰周期有误也会引入额外误差。

3.2.4 相变体系的热容修正

还应注意的是，许多材料在升温过程中存在相变过程，较慢的相变过程对总焓的贡献可以忽略不计；但若存在较快的相变过程，相变潜热会引入明显的额外热容，造成相变区域材料Cp值突增，从而导致实验测得的热扩散系数急剧下降[17]。如图4c所示，Cu2Se、Cu2S和Ag2S等材料在相变温度附近通过实验测得的热容迅速增大，而热扩散系数明显降低，此时如果未考虑相变过程，直接将杜隆-珀替法算得的定值Cp带入式(4)中进行计算，会因热导率偏低而极大程度地高估材料的热电性能[18, 19]。因此，若出现热扩散系数测量结果不连续、突变，或晶格热导率的估算值远低于热导下限等情况，应仔细检查数据并予以关注。因此，建议在报道材料性能时应给出材料热容的获取方式以及潜热对结果可能的影响。

考虑到杜隆-珀替法的计算结果只在一定范围内适用，而通过实验直接测量热容数据波动较大，通常选择用简谐声子项Cph,H和热膨胀项CD的求和计算代替实验测量Cp值。图4d是分别利用杜隆-珀替法、模型计算法计算得到的HfCoSb0.8Sn0.2样品的热容值及该值与LFA-457仪器状态良好时实验测量结果的对比，可以看出高温时热容的简谐声子项接近杜隆-珀替值，加上热膨胀项之后基本可以准确描述样品的实际热容。

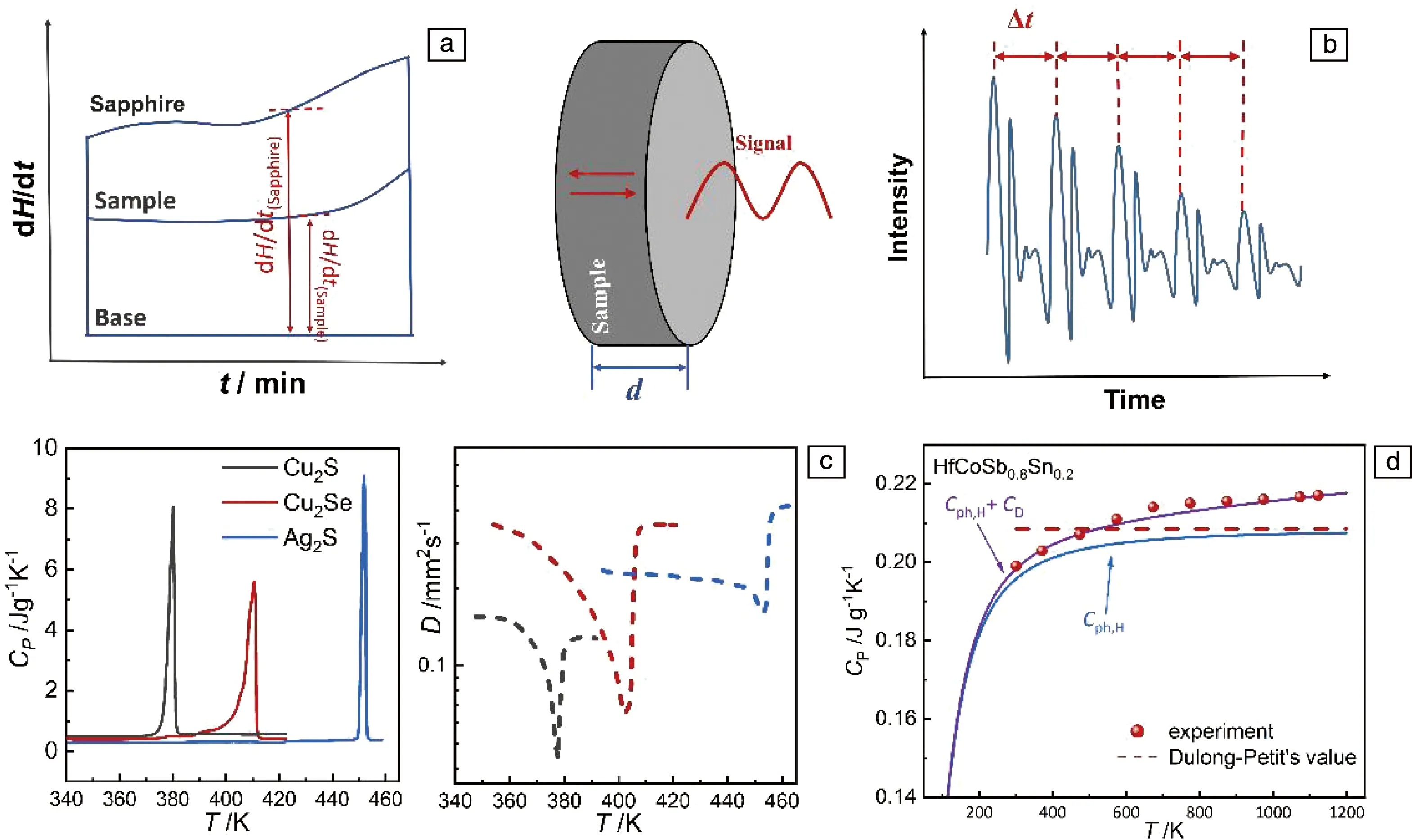
图4 差示扫描量热仪测量原理示意图(a)，反射式时差法声速测试原理图(b)，相变过程中Cu2S、Cu2Se和Ag2Sc热容(左，差示扫描量热仪)和热扩散系数(右，激光闪射仪)随温度的变化关系(c)[18, 19]，不同方法获得的HfCoSb0.8Sn0.2热容对比(d)Fig.4 Schematic diagram of differential scanning calorimeter measurement (a) and measuring sound velocity by reflective TDOA method (b), the heat capacity (left, differential scanning calorimeter) and thermal diffusivity (right, laser flash apparatus) of Cu2S, Cu2Se, and Ag2S during phase transitions[18, 19] (c), comparison of heat capacity of HfCoSb0.8Sn0.2 obtained by different methods (d)

4 室温以下输运性能测试

4.1 电输运性能测试

因为Seebeck系数和电导率随载流子浓度变化趋势相反，在特定的温度下，存在一个最优载流子浓度nopt使材料的功率因子PF=S2σ达最大值。此外，载流子迁移率可以帮助分析材料的微观散射机制，但迁移率并非可以直接测得的物理量，通常利用电导率和载流子浓度的测量结果经后处理得到，因此表征体系在室温以下的载流子浓度对选择合适的掺剂及掺杂量，分析散射机制,优化热电性能有着极其重要的指导意义。

实验室通过霍尔效应测量载流子浓度，原理如图5a所示，将厚度为d的薄片试样垂直置于沿z轴方向的均匀磁场Bz中，在较长的x方向施加电流Ix，载流子受到洛伦兹力后在电场中发生偏转，在y方向产生霍尔电压VH，由此可以测得霍尔系数RH=(VHd)/(IxBz)及霍尔载流子浓度nH=1/|eRH|，材料的导电类型决定了霍尔电场的方向，即霍尔系数的正负，n型为负，p型为正。从公式中可以看出，当待测样品的载流子浓度较高时，直接测得的VH较小，因此对较高载流子浓度的样品在制样时应尽可能使样品厚度d较小，以获得更可靠的测试结果。

由于霍尔效应测量过程中存在不等位电势差V0、Nernst效应引起的电势差VN、Righi-Leduc效应引起的电势差VRL以及Ettingshausen效应引起的电势差VE等。它们与工作电流Ix和磁感应强度B间的关系分别为：V0∝Ix，VN∝B、VRL∝B、VE∝IxB，可以通过电磁场的反转有效消除这些副效应带来的误差。

当采用直流电流时，常利用对称测量法，通过改变电流和磁场的方向分别进行4次测量来消除前3个效应带来的误差，其中VE由于和电流、磁场均相关，无法通过该手段消除，但它带来的误差较小，因此在粗略测量中可以忽略不计。因霍尔效应的建立时间(10-14～10-12s[20])远小于温差建立时间(约几秒)，故采用交流电流可以消除Ettingshausen效应，且VN和VRL对交流电压表的测量值无贡献，令磁感应强度取零还可以测出与磁感应强度无关的不等位电势差V0的大小并扣除[21]。

在这4个副效应中，不等位电势差V0产生的相对误差最大，它与被测试样本身性质有关，制样时应注意保证样品成分及厚度的均匀性、电极探针位置放置的对称性等。

范德堡法可利用反向场互易性，即有外加磁场时，互换电流电压触点同时反转磁场方向测得的电阻相等，而磁场不变单纯互换电流电压触点后测得的两阻值之差即为霍尔电压，不用反转磁场也可消除磁阻偏移和电阻偏移，节约了测量时间。无论是范德堡法还是四点法，都应采用平而宽的被测样品，从而保证样品内部电流均匀分布，且样品厚度要尽可能薄，以减小误差影响。

测量前要检查导线与样品的接触是否良好，可用欧姆表测试样品表面与管脚之间的电阻，阻值过大说明接触不良。可以根据测得的V-B曲线线性关系判断实验数据的可靠性，图5b为GeTe样品在300 K测得的不同接触状况下的V-B曲线，当样品与导线接触良好时测量点线性关系好且测得的载流子浓度与该样品在此温度下的标准载流子浓度更接近[22]。对于磁性热电材料，测得的霍尔数据包括了反常霍尔效应和常规霍尔效应2部分的贡献，进行数据分析时应注意去除反常霍尔效应部分。此外，热电材料大多为重掺半导体，霍尔信号非常低，对外界扰动敏感，所有测量引线应固定并包裹锡纸层，以减少磁感应力或外界干扰引起的导线误差。应注意的是，如果被测样品为本征半导体或测试温度达到样品本征激发温度，载流子浓度会随温度变化迅速变化，相应的双载效应会导致霍尔信号噪声大，测量结果不准确。

此外，Quantum Design公司开发的综合物性测量系统(physical property measurement system，PPMS)中的电输运测量选件(electronic transport option，ETO)也可以在较低温度下实现材料电性能的测试[11]，PPMS室温以下的热学测试功能将在下一节中展开讲解。

图5 霍尔系数测量示意图(a)，样品和导线接触良好和不好时测得的霍尔数据对比(b)Fig.5 Schematic diagram of Hall coefficient measurement (a), comparison of V-B curves in Hall coefficient measurement with good and poor contact (b)

4.2 热输运性能测试

PPMS的热学测量功能分为比热测量选件(heat capacity option，HCO)和热输运选件(thermal transport option，TTO)。其中HCO采用双τ模型对样品升温及冷却过程的弛豫曲线进行拟合，可测量极低温度下样品的比热，但为了使测量过程中平台和样品能建立起稳定的热平衡，升温/降温过程的时间应足够长，较为耗时。对于热电材料，通常直接利用PPMS中的TTO模块测量样品热导率κ。

TTO系统测量热导率κ的装置原理图如图6a所示。根据施加的电流I、加热功率P、产生的温差ΔT、电势差ΔV和热电偶间距ΔL可得出Seebeck系数、热导率和电导率。其中，单一测量模式利用稳态法，通过公式κ=(P/ΔT)(ΔL/S)计算得到样品在某一固定温度下的热导率，但测量温度的建立使其耗时较长。而连续测量模式主要与双τ模型进行拟合，从而推导出温度变化过程中样品的热导率，热脉冲过程中测得的温差ΔT和电势差ΔV随时间的变化如图6b所示，脉冲前后会分别进行2次交流电阻率测量，取平均值作为样品电阻率。根据需求可选择2种样品安装的方法。图6c给出了双线法安装条形和盘形样品的示意图，垂直安装在圆盘上的样品长度应在3～20 mm范围内。这种方法只需2条引线，方便但准确性较差。一般当样品的热阻和电阻远大于导线的热阻和电阻时才使用双线法。当样品热阻和电阻太低，无法忽略导线接触电阻的影响时通常采用四线法，如图6d所示，4个探针单独与样品连接。考虑到样品中的热扩散时间不能过长，被测样品长度一般不超过10 mm。

TTO系统可以同时测量样品的Seebeck系数、交流电阻率和热导率，并直接给出其zT值。图6e对Nb0.9Hf0.1FeSb样品用PPMS进行多参数同时测试，与传统的各参数独立测试相比，得到的zT结果在低温下吻合较好[23]。

由于样品和测量组件及周围环境间的热辐射，200 K以上利用PPMS测得的热导数据会观察到明显上升，要对测得的数据进行热损失校正，校正后的热导K见下式：

K=(I2R-Prad)/ΔT-Kshoes

(8)

Kshoes=aT+bT2+cT3

(9)

(10)

其中，R为加热电阻阻值，Prad为样品辐射，Kshoes是测量组件的标准热导估计值(a、b、c为常数)，σT是斯特藩-玻尔兹曼常数，A是样品总表面积，ε是辐射面红外发射率，Tcold/Thot分别为冷热温度计测量期间的平均温度。可通过以下几个方式减小热辐射引入的测量误差：① 增大样品几何因子A/ΔL，以使样品热导远高于辐射热导；② 用已知红外发射率的材料涂覆样品表面；③ 尽可能减小样品的辐射表面积。由于辐射热损失很难精确预估，故300 K以上PPMS热导测试的误差可达±1 mW/K。

图6 综合物性测量系统(PPMS)中：(a)装置原理图，(b)样品冷热端的热脉冲以及温度和电压响应，(c)双线法导线图，(d)四线法导线图；利用PPMS与LFA+LSR获得的zT值对比(e)[23]Fig.6 Physical property measurement system (PPMS): (a) schematic structure diagram, (b) heat pulse and temperature and voltage response at hot and cold thermometer shoes in an idealized sample, (c) examples of leads mounted in two-probe configuration, (d) example of leads mounted in four-probe configuration; comparison of zT values obtained with PPMS and LFA+LSR (e)[23]

5 其他注意事项

利用Harman法测得的zT值受材料各向异性影响不大，但通过分别测量热电参数算得的zT值与测量的取向方向强烈关联。通常电性能和热性能测试对样品的几何形状要求不同，往往需要对同组分的多个样品进行表征才能得到该材料完整的性能。对于层状或类层状结构的材料，沿不同方向会有输运性质上的各向异性，因此对于取向多晶或单晶样品，应注意沿同一方向测量其热学与电学性能。以多晶Bi2Te3基材料为例，通常会利用热压等工艺手段提高其织构程度[24]，图7a为p型Bi2Te3分别沿垂直于压力的x方向和平行于压力的z方向测得的热电参数，不同取向测得的Seebeck系数差别不大，但沿x方向的电导率和热导率明显高于沿z方向的，最终算得的zT值相近，若误取x方向电性能参数与z方向热性能参数进行组合计算，将得到错误的高zT值[24-26]。

样品本身几何因子，物相纯度以及取向情况也会影响到性能测试结果，一些合成后处理也会改变材料性能，如图7b所示，Ba0.44Co4Sb12-0.43%C60样品退火前后测得的S差别较大[7]，故在进行热电性能表征之前要检查样品均匀性，并尽量保证制备工艺不变或为单一变量。X射线衍射、X射线能谱仪、电子探针显微分析仪常用于分析样品物相组成，可帮助确认实际组分与名义组分偏差、体系内是否有杂相存在、取向各向异性等情况。

不仅如此，随着材料器件化需求的增大，材料的放量制备是必需的，但体积增大会使其宏观均匀性更难保证，化学成分以及微观结构等可能会随着位置变化发生变化，图7c为放量制备的p型half-Heusler合金(Nb0.8Ta0.2)0.8Ti0.2FeSb，复杂的成分和高熔点的组元导致大尺寸样品的均一性出现波动，从制得的铸锭上切取不同位置的样品进行Seebeck系数的测量，可以看到Seebeck系数的变化范围高达15%[27]。故为了保证计算的zT值真实有效，应从块体上切取位置尽可能相近的样品进行同一取向的热电测试。

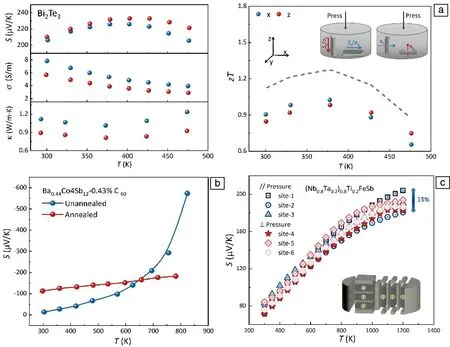
图7 多晶Bi2Te3材料热电性能的各向异性(a)[25]，Ba0.44Co4Sb12-0.43%C60样品退火前后测得的Seebeck系数对比(b)[7]，p型(Nb0.8Ta0.2)0.8Ti0.2FeSb大尺寸样品不同位置处Seebeck系数对比(c)[27]Fig.7 Anisotropy of thermoelectric properties of polycrystalline Bi2Te3 material (a)[25], comparison of Seebeck coefficients measured before and after annealing of Ba0.44Co4Sb12-0.43%C60 samples (b)[7], comparison of Seebeck coefficients at different positions of p-type (Nb0.8Ta0.2)0.8Ti0.2FeSb compounds (c)[27]

6 结 语

要获得热电材料的热电优值，通常需要单独测试材料的多个电学和热学输运参数，因此每个参数测量的准确性尤为重要。受制于不同测试手段及其原理影响、不同仪器的系统误差以及实验人员的实际操作，热电材料的性能数据可能存在较大偏差，这会导致不同课题组的数据对比分析难度加大，不利于热电领域系统研究的开展。虽然无法针对不同的研究组制定统一的测量标准，但可以通过优化测量条件、样品质检、原始数据检查等尽可能地排除一些系统误差，大大增加测量数据的可信程度。

本文概述了应用于热电块体材料的几种常见的性能表征方法及原理，举例说明了测量过程中的一些不当操作、副效应可能会引入的误差，重点讨论了样品制备、测量结果校正以及数据质量判断的方法，旨在帮助该领域的研究人员理解测试原理，选择更合适的表征方法，获得更为可靠的数据值，以助力后续的热电机理分析和性能调控研究，为热电领域的进一步发展奠定基础。