小型断路器双金属片瞬时热分布研究

2023-01-11戴铭磊

现代建筑电气 2022年10期

周阳, 王东, 戴铭磊

[国网湖南省电力有限公司建设分公司(咨询公司), 湖南长沙 410000]

0 引言

断路器主要用于低压配电线路或用电设备中,在电力系统中起着重要的控制和保护作用。如今对用电保护的要求越来越高,断路器的热脱扣问题一直困扰着各类断路器的生产者。在脱扣机构确定的情况下,能够正确地设计并选用双金属材料性能是解决问题的关键[1]。当前,生产厂家主要通过实验进行热分析,但这样使产品设计的费用增加,周期加长。如果能够在产品的设计阶段采用虚拟样机技术进行热分析,就可以减少设计成本和缩短制作周期,因此,研究双金属片的热分析具有重要的实际应用价值和发展前景[2]。

近年来,仿真技术发展迅速。为了降低研发成本和缩短研发周期,国内外许多专家和学者对各种电气设备进行了仿真研究。在国内,许文良等[3]研究了低压断路器瞬态电热分析的仿真计算方法;徐宏宇等[4]利用Ansys软件计算了低压配电柜的稳态温度场分布以及气流场分布。

国外多位学者也对温升仿真进行了许多研究。Barcikowski等[5]研究发现小型断路器内部的对流与辐射传热过程对断路器导电回路稳态温升的影响可以忽略;Yoon等[6]使用了一种电磁场-热场耦合的仿真方法来计算GIS母线导体的热分布特性,并且在仿真中考虑了GIS母线材料属性的非线性特性以及辐射传热对仿真结果的影响,并进行了相对应的实验[6]。

本文采用Ansys有限元仿真软件研究了某型号断路器双金属片的瞬时温度分布规律以及瞬时形变,并利用温升实验平台测量双金属片关键部位的温升,对实验结果与仿真结果进行对比与验证,为产品的优化设计提供理论依据。

1 基础理论和计算方法

1.1 导热系数的计算

在热分析中,金属导体的导热系数决定了整个模型的温度大小,每种材料的导热系数随金属的纯净程度、温度、压力以及材料结构等因素变化,通常情况下,温度起着决定性的作用。在工程计算中,材料导热系数与温度的关系如公式(1)所示:

λ=λ0(1+bθ)

(1)

式中:λ——材料工作时的导热系数;

λ0——273.15 K时材料的导热系数;

b——材料工作时的温度;

θ——实验所确定的常数,由材料本身决定。

由传热学理论可知,随着温度升高,铜合金和铝合金的导热系数变化较小,因此,在工程计算中,在一定的温度范围内,可以认为其导热系数不变,铜合金导热系数为400 W·(m·K)-1,铝合金导热系数为144 W·(m·K)-1。

1.2 散热系数的计算

模型中的传热机制包括热传导、对流和辐射。采用在散热表面赋热对流换热系数的方式来模拟对流传热。双金属片被塑料外壳里面的空气所包裹,空气的流动受到限制,对流传热属于有限空间自然对流传热,如公式(2)所示:

q=αcon·A0·(Tf-T0)

(2)

式中:αcon——材料的对流换热系数;

A0——材料的对流换热面积;

Tf——环境温度;

T0——材料表面温度。

公式(2)中,αcon与周围流体的特性有关,本文根据流体的相似理论计算对流散热系数。在工程计算中,广泛应用的自然对流实验关联式如式(3)～式(5)所示:

(3)

Nu=C(GrPr)n

(4)

(5)

式中:Gr——Grashof数;

g——重力加速度;

β——体积膨胀系数;

Δt——物体表面与室温的温差;

v——运动黏度;

Nu——Nusselt数;

C——常数,取决于材料本身;

Pr——Prandlt数;

n——常数,取决于不同换热问题;

αcon——对流换热系数;

λ——材料热导率;

lc——材料表面面短边长度。

辐射散热也是一种主要的散热方式。热辐射是由电磁波传播能量,根据Stefan-Boltzmann定律,物体的辐射散热qi以及辐射散热系数αrad计算如公式(6)和公式(7)所示:

qi=σFijεiAi(T4f-T40)

(6)

(7)

式中:σ——Boltzmann常数;

Fij——材料系数,由材料本身决定;

εi——发射率;

Ai——辐射散热面积;

Tf——环境温度;

T0——材料表面温度。

2 仿真模型建立

小型断路器模型如图1所示,外接的连接导线通过左右两侧的螺钉固定,位于上方的是断路器的操动机构,包括手柄、连接杆和转板等。在断路器闭合时,动静触头接触进行导电;位于断路器左侧的是螺线管以及灭弧栅片,用于断路器的短路保护;双金属片位于断路器的右侧,双金属片左侧通过导线与动触头相连接,右侧通过铜片与右侧外接导线连接。

图1 小型断路器模型

本文重点研究双金属片的瞬时温升,双金属片产热模型如图2所示。

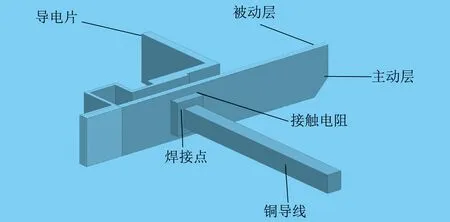
图2 双金属片产热模型

焊接点与主动层间有0.1 mm厚的导电接触层,接触电阻的电阻率与热导率如式(8)和式(9)所示:

(8)

(9)

式中:ρ——电导率;

R——电阻;

s——接触电阻横截面积;

l——接触电阻长度;

λ——热导率;

L——洛伦兹系数;

T——热力学温度。

仿真流程图如图3所示,首先利用UG软件对双金属片模型进行简化,得到双金属片仿真模型;然后,将模型导入Ansys APDL模块中,赋予各个部件材料属性,并进行有限元网格剖分;最后,调整模型的边界条件,仿真计算后可以得到双金属片的瞬时温度和形变结果。

3 仿真与实验结果及分析

3.1 仿真结果及分析

仿真所使用的双金属片参数取自额定电流为63 A的小型断路器,双金属片主要部件材料属性如表1所示。

通过Ansys软件仿真计算后得到了不同时间下双金属片的温度分布云图以及最大位移,在环境温度16 ℃,通46 A的50 Hz交流电时,63 A断路器双金属片在66,216,3 600 s时的温度分布云图分别如图4～图6所示。

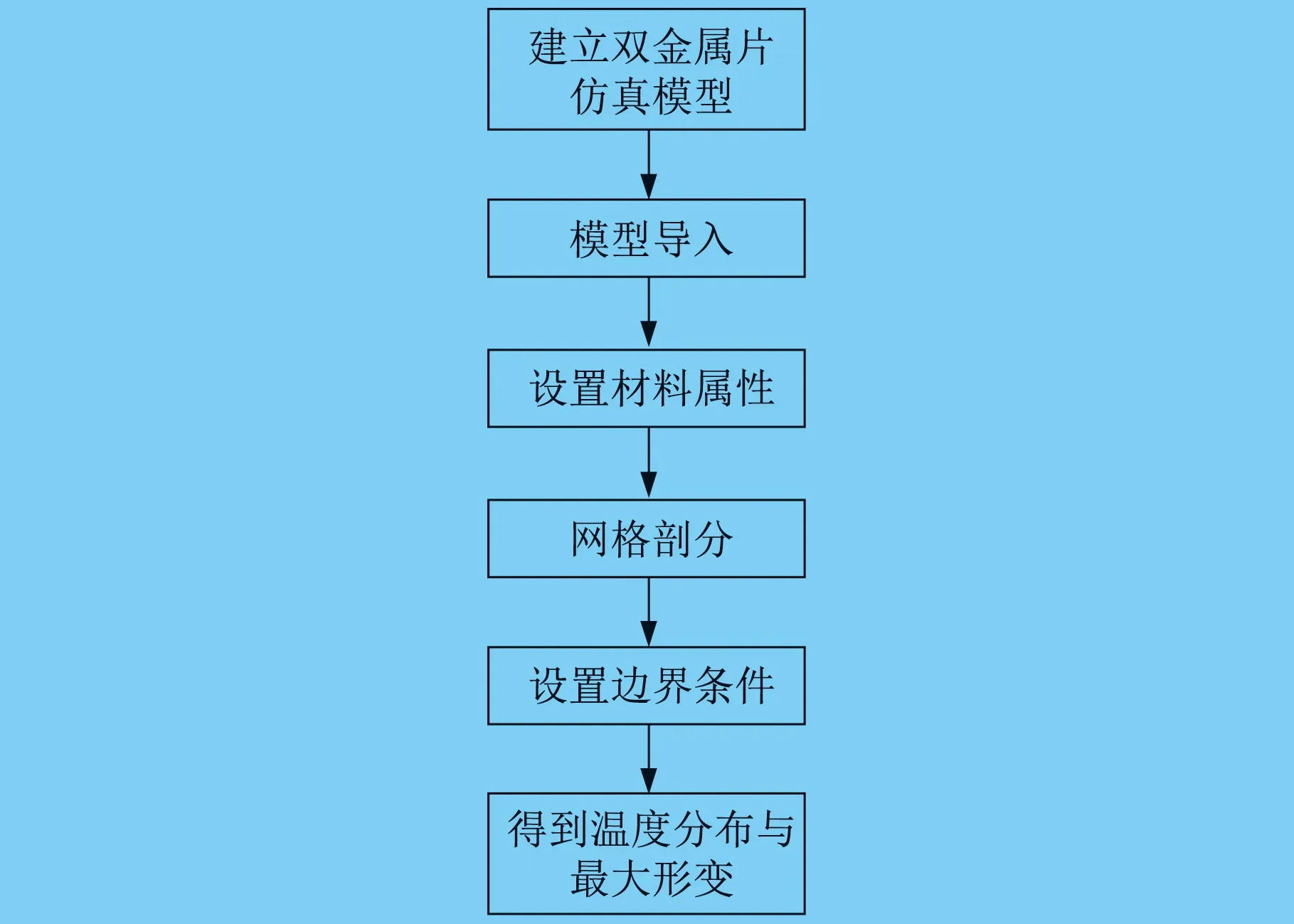
图3 仿真流程图

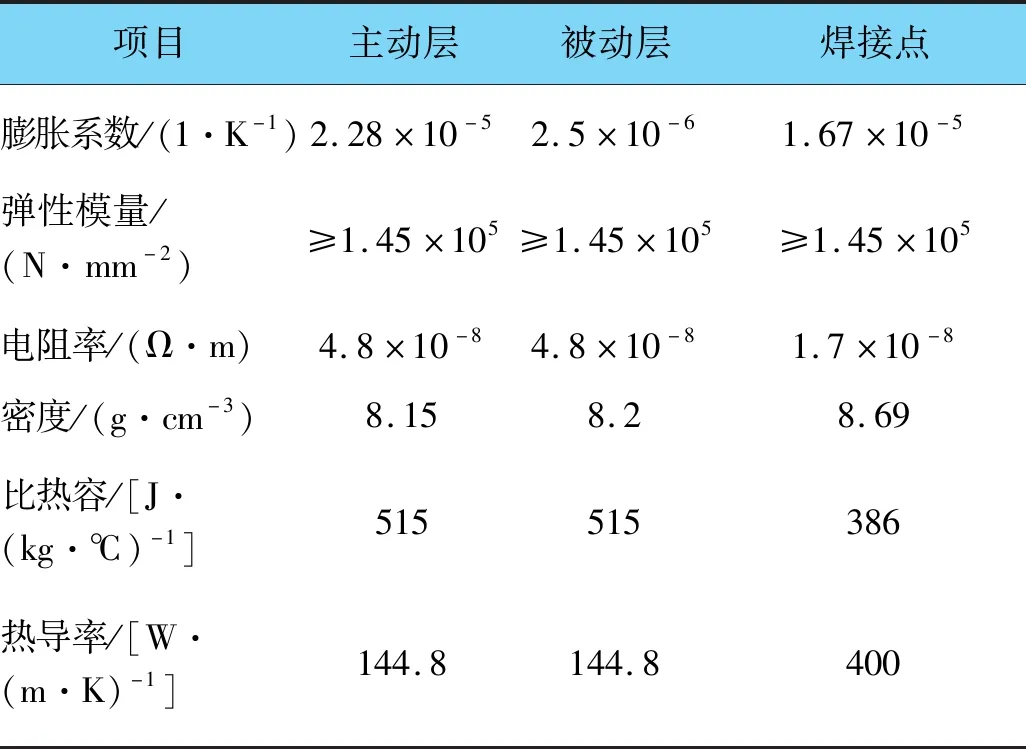
表1 双金属片主要部件材料属性

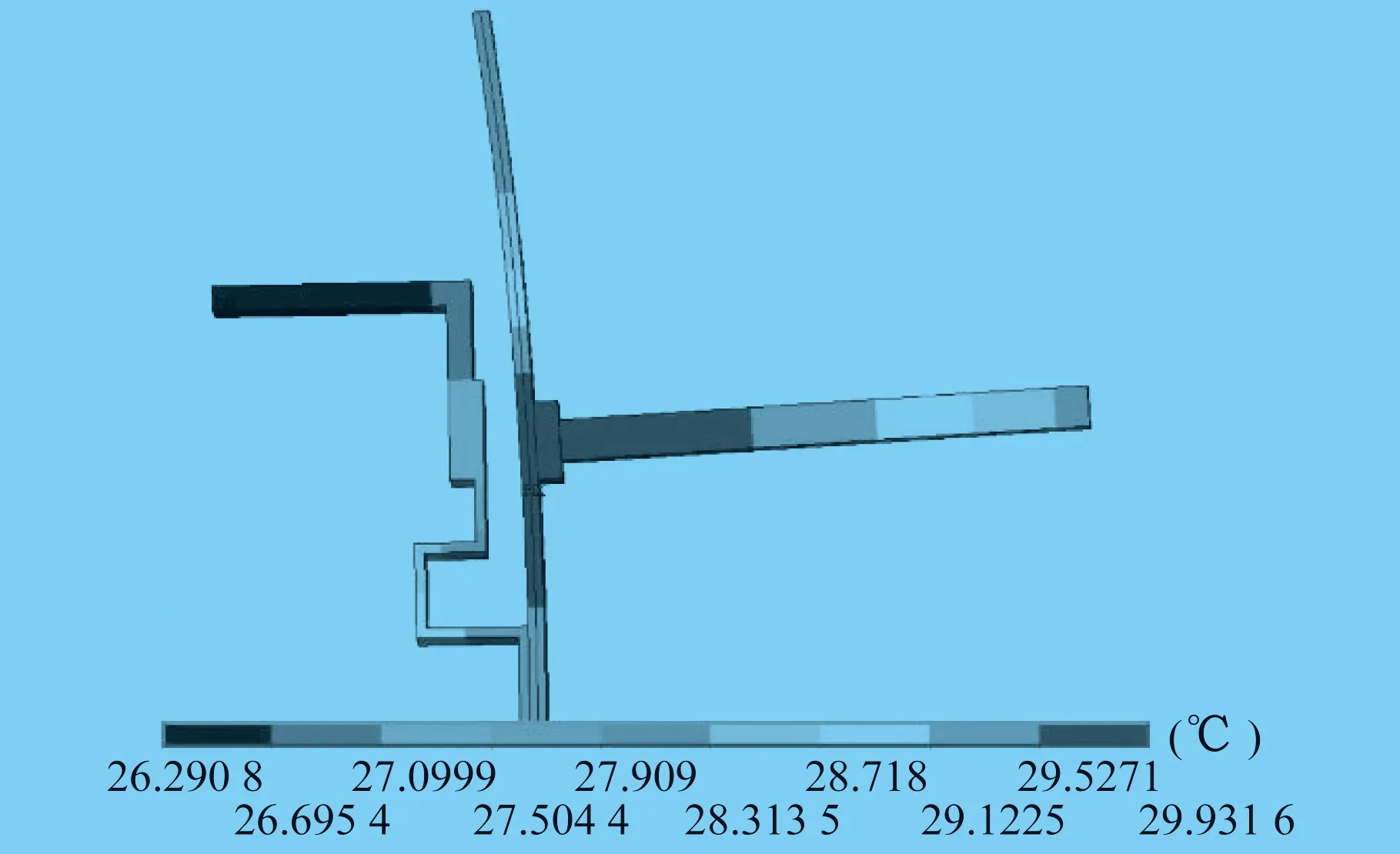
图4 66 s时双金属片温度分布云图

由图4～图6可以看到,63 A断路器通46 A电流时,双金属片的温度分布相似,在焊接点处的温度最高,在66 s时最高温度为29.93 ℃,在216 s时最高温度为40.97 ℃,在3 600 s时最高温度为44.68 ℃。导线上的温度分布规律为靠近焊接点的导线温度最高,越远离焊接点,导线的温度越低。双金属片上的温度分布同样是接近焊接点处的温度高,远离焊接点的温度较低。而导电片上的温度是最低的。在此条件下,63 A断路器双金属片在66 s时的最大位移为0.633 mm,在216 s时的最大位移为0.837 mm,在3 600 s时的最大位移为0.945 mm,最大位移点在双金属片的顶端。

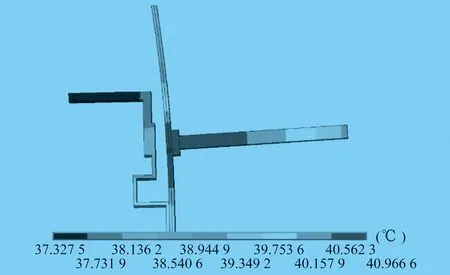
图5 216 s时双金属片温度分布云图

图6 3 600 s时双金属片温度分布云图

3.2 实验结果及分析

为了验证仿真模型,本文完成了63 A额定电流断路器的双金属片温升实验。实验中,变压器提供稳定的交流电压,通过电流线圈测量实验电流,使用热电偶测量温升,所测试断路器如图7所示。

63 A额定电流断路器所通电流为46 A,双金属片温升测量点如图8所示,分别在双金属片顶端、焊点处、双金属片底端用温度传感器测量温升,至温升到达稳定为止。

图7 所测试断路器

图8 双金属片温升测量点

63 A断路器在3个测量点的温升实验结果如图9所示。由图9可以看到,随着实验时间的推移,双金属片的温度不断上升,3个温度测量点在300 s后温度上升会显著变慢,380 s后温度不变,1号测量点最高温度为40.8 ℃,2号测量点最高温度为45.3 ℃,3号测量点最高温度为42.3 ℃。

图9 63 A断路器在3个测量点的温升实验结果

63 A断路器在3个测量点的稳定温升仿真结果和实验结果对比如图10所示。由图10可以看出,双金属片温升的增长趋势大致相同,随着通电时间的增加,双金属片温度不断上升,实验和仿真温度变化趋势基本相同,在400 s时到达稳定温升,仿真在380 s时到达稳定温升。当达到稳定温升时,1号测量点的温度为42 ℃,与仿真结果温升差为1.2 K;2号测量点的温度为44.6 ℃,与仿真结果温升差为0.7 K,3号测量点的温度为43.5 ℃,与仿真结果温升差为1.2 K。63 A断路器的双金属片温升仿真结果与实验测量值相吻合,表明了仿真方法的正确性。