关于高中数学建模教学的实践

山东省邹平市第一中学 李 猛

数学课程标准明确指出，建模能力是学生核心素养之一，借助建模教学能锻炼学生创造性思维，最重要的是对所学知识形成深入理解，为更好地应用知识分析和解决问题奠定基础，实现预期课程教学目标。

一、借助问题情境

情境教学是课堂教学常见方式，高中数学教师可运用问题情境开展建模教学，促使学生在探索、思考、提问、分析以及建模等一系列过程中高效解决问题，并对所学知识产生深入理解，锻炼思维能力。学生思维在问题情境驱动下相对开放，他们在此过程中提出各种抽象复杂且创新性问题，这对数学教师综合素养和知识技能等提出较高的要求。教师需要积极思考该如何引领学生学习，因此需要在为学生传授知识和技能的同时不断延伸自身知识储备深度与广度。

对此，教师可从以下方面借助问题情境开展建模教学。首先，借助问题情境导入新知。教师在数学建模教学中应为学生创设愉悦、和谐的课堂环境并积极鼓励学生大胆想象和思考，使不同思维和意见观点在良好课堂氛围中发生碰撞并产生智慧火花，不断提升学生思维层次。例如，在学习均值不等式定理相关知识时，教师设置以下问题：“某超市在中秋节开展促销活动，为吸引客源，共涉及以下三种降价销售方案：①首次打a折，第二次打b折销售；②首次打b折销售，第二次打a折销售。③两次销售均打折，请问，上述三种打折销售方案哪种最为划算。”学生经思考和相互讨论后得出以下解题要点：即对ab与大小进行比较。上述题目紧贴学生现实生活，教师为学生设置抽象概括且符合学生实际情况的问题情境，以生动形象方式为学生呈现生硬抽象的均值不等式定理。大部分高中数学应用题在解答中都需运用均值不等式，故而，创设紧贴生活的问题情境导入新知识能调动学生探究知识积极性，更能活跃学生数学思维。其次，挖掘纯数学问题生活原型，不断增强学生建模意识。现实生活生产蕴含大量数学问题，将数学知识和技能结合现实生活生产能增强学生灵活运用知识能力。例如，某制造厂今年一共生产近5万吨产品，如果每年平均产量高于上一年10%，请问从今年起在几年内能实现总产量30万吨目标？教师在讲解题目时要先指导学生分析前几年产量，即今年为5万吨，明年则是5+5×10%＝5×1.1，那么后年则为5×1.1+5×1.1×10%＝5×1.12，学生在观察中归纳总金额公比q＝1.1后构建等比数列模型。虽然上述解答过程较为缓慢，然而能促使学生深入理解问题，提升建模能力。

二、借助信息技术

事实上，现实生活中涵盖大量数学知识，学习数学知识目的之一也在于更好地解决实际问题，尤其会应用几何图形、函数、方程等知识，故而运用“互联网+建模”能直接降低题目难度，提高解题效率。检验和完善解题模型是数学建模思想下重要思维环节之一，类似于常规学习总结与检验，有利于帮助学生充分把握自身在数学建模活动中出现的解题错误和认知不足，促使学生高效理解和掌握不同类型解题模型使用条件，并在归纳总结、反思、纠正等一系列活动中建立正确建模认识，为提升建模素养做好铺垫。例如，在学习数列相关知识时，教师结合现实生活常见的银行存款本息计算设计问题，需要学生结合真实银行存款月利率与本息计算公式对某个周期内本息总和进行计算，在此过程中应用数列知识。教师在教学过程中运用信息技术为学生建立模型并基于此凸显数列模型思想，促使学生运用等比数列求和规律分析和解决实际问题。与此同时，鼓励学生独立思考问题，再以小组形式相互讨论分析，遇到疑惑之处可运用平板和互联网中的学生端口发送给教师，随即教师为学生实时答疑解惑，还可在学生小组讨论时参与其中，提升学生学习效率。

三、借助小组合作

小组合作是课堂教学主要方式，能较好地体现学生主体作用，汇集多元思维，帮助学生深入理解所学知识，提升学习效率和质量。在建模教学中应用小组合作学习能增强学生发现问题、分析问题和解决问题能力，在合作中实现核心素养目标。

以“货船进出港时间问题”教学为例，该知识点重点为引导学生观察和详细分析数据并在此基础上建立三角函数模型，促使学生敢于想象和表达。表1为某港口在某季节每日时间与水深关系。

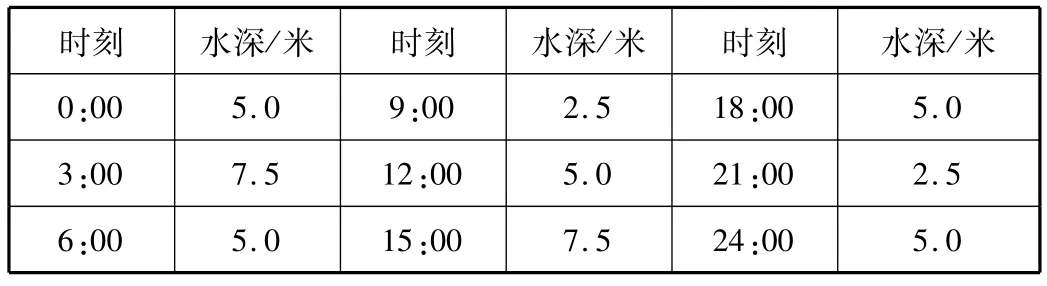
表1 时间与水深关系

问题①选取一个函数对该港口的水深与时间函数关系进行近似描述并给出整点水深近似数值。问题②若一条货船吃水深度为4米，在安全规定下要求船底与洋底间距离具有1.5米安全间隙，请问该条船在何时才能驶入港口？在港口停留多少时间？问题③若某条船吃水深度为4米，设置1.5米的安全间隙，于2：00时卸货，其中该船吃水速度以每小时0.3米速度不断减少，请问该船在何时需停止卸货并将船驶向深水域？

具体建模教学活动如下。（1）活动要求：将全体学生分为5个小组讨论分析上述三个问题，每个小组选派一名学生上台汇报讨论成果并阐述心得体会。（2）观察／分析以及模拟图象。A小组：“我们认为该函数为具有周期性变化特征的函数。”D小组：“为何会产生此猜想？”B小组：“将时间和水深分别设为横坐标与纵坐标并在直角坐标系中画出散点图，如图1所示。”

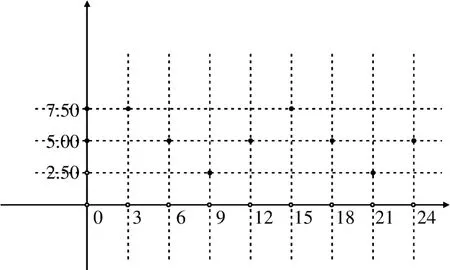
图1 时间与水深散点图

教师：大家观察散点图后是否能绘制出对应函数图像？F组：“该函数图像为一条平移变换后形成的复合型三角函数图象，如图2所示。”教师：请阐述理由。F组：“运用平滑曲线连接后发现振幅与初相都发生不同程度变化。”教师：推理得很合理，如果想解决第一个问题需作出相应函数解析式。

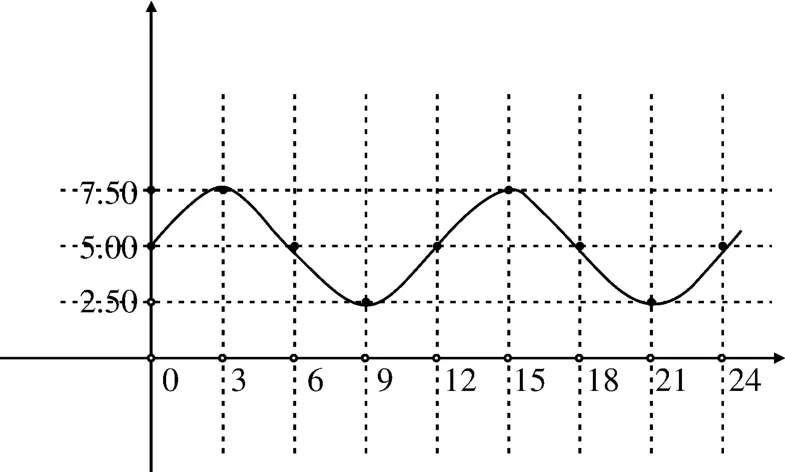
图2 时间与水深复合型三角函数图形

（3）猜想验证、推理论证以及建立模型。在此之前已顺利作出三角函数模型图象，随即让学生回忆之前所学三角函数模型并写出。随即有学生写出：三角函数模式y＝A sin（ωx+φ）+h。教师：通过数据与图象并在讨论中计算该题目函数模型。由A组学生解析：从函数图象和数据得知：A＝2.5，h＝5，T＝5，φ＝0，由得故而可运用表示港口水深y与时间x关系。建立函数模型目的在于解决问题，数学教师可鼓励学生积极大胆猜想并运用数据对函数图象进行模拟，在合作交流中有效推导、计算、验证函数模型，以此强化学生逻辑推理能力。

四、结语

总之，建模在学生学习和教师教学中发挥着不可小觑的作用。通过开展建模教学能简化学生理解知识难度，并强化逻辑思维和创新思维，提升学生数学综合素养和数学教学质量，对学生未来发展有着重要现实意义。