考虑局部渗流的Biot孔隙弹性模型改进
2023-01-10时鹏丁海琨王国平李思亦崔新豪李文博
时鹏,丁海琨,王国平,李思亦,崔新豪,李文博
(1.中国石油集团测井有限公司测井技术研究院,陕西西安710077;2.中国石油天然气集团有限公司测井技术试验基地,陕西西安710077;3.中国石油集团测井有限公司国际合作处,陕西西安710077)
0 引 言
声波在孔隙介质中传播时,其速度、频散和衰减受孔隙介质骨架和孔隙流体性质影响[1-7]。在工程应用中可通过测量孔隙介质中传播的声波的速度、频散和衰减数据获得孔隙介质的力学参数、孔隙度、渗透率以及辨识孔隙流体种类[8-10]。孔隙介质的这一波动性质在应用地球物理领域有着重要意义,受到力学、地球物理学研究者的广泛关注。在油气勘探领域,声波测井方法理论上可获得比其他测井方法更全的储层信息。从1956年开始,Biot[11-13]在Frenkel关于孔隙弹性研究的基础上进行了系列研究,建立起流体饱和孔隙介质波动理论。该理论预测孔隙介质中存在两种纵波,并被Plona[14]实验证实。随后,Biot理论被广泛认可并被应用于声波测井方法研究[15-20]。
然而实验结果表明经典Biot模型(简称Biot模型)明显低估了孔隙介质中传播的声波的衰减,并未正确反映流体黏性对弹性波速度、频散和衰减的影响[21-22]。因此,基于经典Biot理论(简称Biot理论)的声波测井方法未被广泛应用于储层渗透率评价。为解决这一问题,研究者尝试引入喷射流效应对Biot模型进行修改。然而现有的修正模型都存在未解决的问题,因而限定了这些模型的使用范围[22-23]。为合理解释含液饱和孔隙介质中的声波性质,需要建立更合理的孔隙介质弹性模型。本文对Biot理论中的基本方程进行分析,指出各个方程的物理意义。在此基础上,对Biot模型进行修正,并通过对比修正模型计算的声波衰减与实验测量的声波衰减验证修正模型的有效性。最后,基于修正模型进行井孔声场模拟,并分析地层局部渗流和渗透率变化对井孔声场的影响。
1 Biot模型与模型修正
Biot理论是在如下假设下建立的:①含液饱和孔隙弹性介质满足小变形假设,本构方程、耗散方程和能量方程为线性方程;②连续介质力学理论适用于可测量宏观量,Biot理论中的宏观量可通过其微观量的体积平均表示;③孔隙介质中传播的机械波满足长波假设;④孔隙介质满足恒温条件;⑤流体受到的力为静水压力;⑥流体相是连续的,封闭孔道不贡献孔隙度;⑦孔隙介质的骨架满足各向同性[24]。Biot理论由4个基本方程构成,在谐波下可表示为[22,24]
τ=(H-2G)(·u)I+C(·w)I+
G(u+uT)
(1)
-p=C·u+M·w
(2)
(3)
-iωw=(-p+ω2ρfu)k(ω)/ηf
(4)
式中,H、C、M和G为孔隙介质弹性系数,Pa;p为压强,Pa,描述孔隙流体受到的压力;τ为应力张量,Pa,描述流体填充各向同性孔隙介质的总应力;w和u为渗流位移和骨架位移,m;ω为角频率,rad*·m1;k(ω)为动态渗透率,D(1)非法定计量单位,1 rad=(180/π)(°);1 D=0.987 μm2,下同;ρf为流体密度,kg·m-3;ηf为黏度系数,Pa·s;ρ为孔隙介质密度,kg·m-3;I为二阶单位张量;i为虚数单位。
Biot理论的4个基本方程中,式(1)和式(2)为流体饱和孔隙弹性体的应力-应变关系,式(3)和式(4)为流体饱和孔隙弹性体的运动方程。式(3)描述构成孔隙介质的微元在总应力作用下的整体运动,式(4)为广义达西定律,描述孔隙流体与固体间的相互作用。Biot理论认为含液饱和孔隙介质的声波衰减与频散来自于流体相对固相骨架流动时的黏性耗散。即式(4)决定Biot理论中声波的耗散与衰减,这说明可通过修正式(4)来解决Biot理论低估孔隙介质声波衰减的问题。
本文通过引入局部渗流效应来解决Biot模型低估孔隙介质声波衰减的问题。假设孔隙介质的孔道二维剖面结构如图1所示,当纵波自上而下传播时,孔隙介质在应力作用下发生体积变化,进而引起孔隙体积变化。孔隙介质体积变化使得孔隙流体从体积压缩的部分向体积膨胀的部分流动,形成孔隙流体的宏观渗流。将孔隙介质孔道看作两个相互垂直且交叉的孔道[见图1(a)],不难发现在垂向应力作用下孔隙介质的体积发生收缩时,水平方向孔道的体积变化大于垂向孔道的体积变化。因此,在垂向压力下孔隙流体的渗流虽然宏观上沿垂向运动,但这一宏观渗流在微观上主要由横向孔道中流体渗流引起。Biot模型只考虑了垂向应力产生的垂向压力梯度引起的宏观渗流,未考虑微观渗流对宏观渗流的贡献。Dvorkin等[21]在类似解释下提出了Biot-Squirt(BISQ)模型,并引入了未知参数喷射流长度反映耗散大小。该模型认为在垂向压力作用下孔隙流体水平流向与本文模型中描述的水平向渗流方向相反。

图1 孔隙介质二维剖面示意图
如上所述,在垂向应力作用下孔隙流体的垂向宏观渗流主要由横向孔道中的流体渗流引起。这说明在孔隙介质体积发生变化的过程中,孔隙介质微元内部水平方向的压力梯度会明显高于垂向压力梯度。因而宏观上垂向压力梯度一定时,单位时间内考虑局部渗流的孔隙介质宏观渗流量应明显大于不考虑局部渗流的孔隙介质宏观渗流量。对于真实孔隙介质,两者的具体差异应由孔隙介质孔道结构决定。为此,本文在式(4)中引入一个修正参数β反映局部流动对宏观渗流的贡献,修正后的孔隙流体与固体间相互作用可用式(5)描述。
-iωw=(-p+ω2ρfu)βk(ω)/ηf
(5)
即在相同压力梯度下,考虑局部流动时流过孔隙介质微元的渗流量是不考虑局部流动时渗流量的β倍。对于不同种类的岩石,其构成颗粒的弹性模量不同。同时岩石形成过程中环境不同,固相颗粒堆积形成的孔隙介质空间结构也不同。因此,β的值应由岩石种类和所处环境决定。对于岩石的结构和构成岩石骨架固体颗粒的性质,这两者都已知的孔隙介质,其本构关系和β的值可利用细观力学通过解析推导或有限元计算获得。
2 修正模型有效性验证
通过比较修正模型计算结果与实验测量结果验证修正模型的有效性。图2显示了模型计算的衰减系数与实验数据对比。在利用修正模型计算衰减系数时,采用表1中岩样I的岩石物理参数。图2中实线和虚线分别表示声源频率为1 MHz、β分别为1.0(Biot模型)和18.0(修正模型)时计算的纵波衰减系数。图2中黑色圆点为声源频率为1 MHz时,实测的岩样纵波衰减系数。比较Biot模型与修正模型计算的衰减系数可知:通过改变修正参数β,修正模型可以有效解决Biot模型低估岩石衰减的问题。比较模型计算结果与实测数据可知,修正模型计算的衰减系数随渗透率的变化趋势与实测结果相同,合理地选择修正参数β可使理论计算结果与实验测量结果在同一量级。
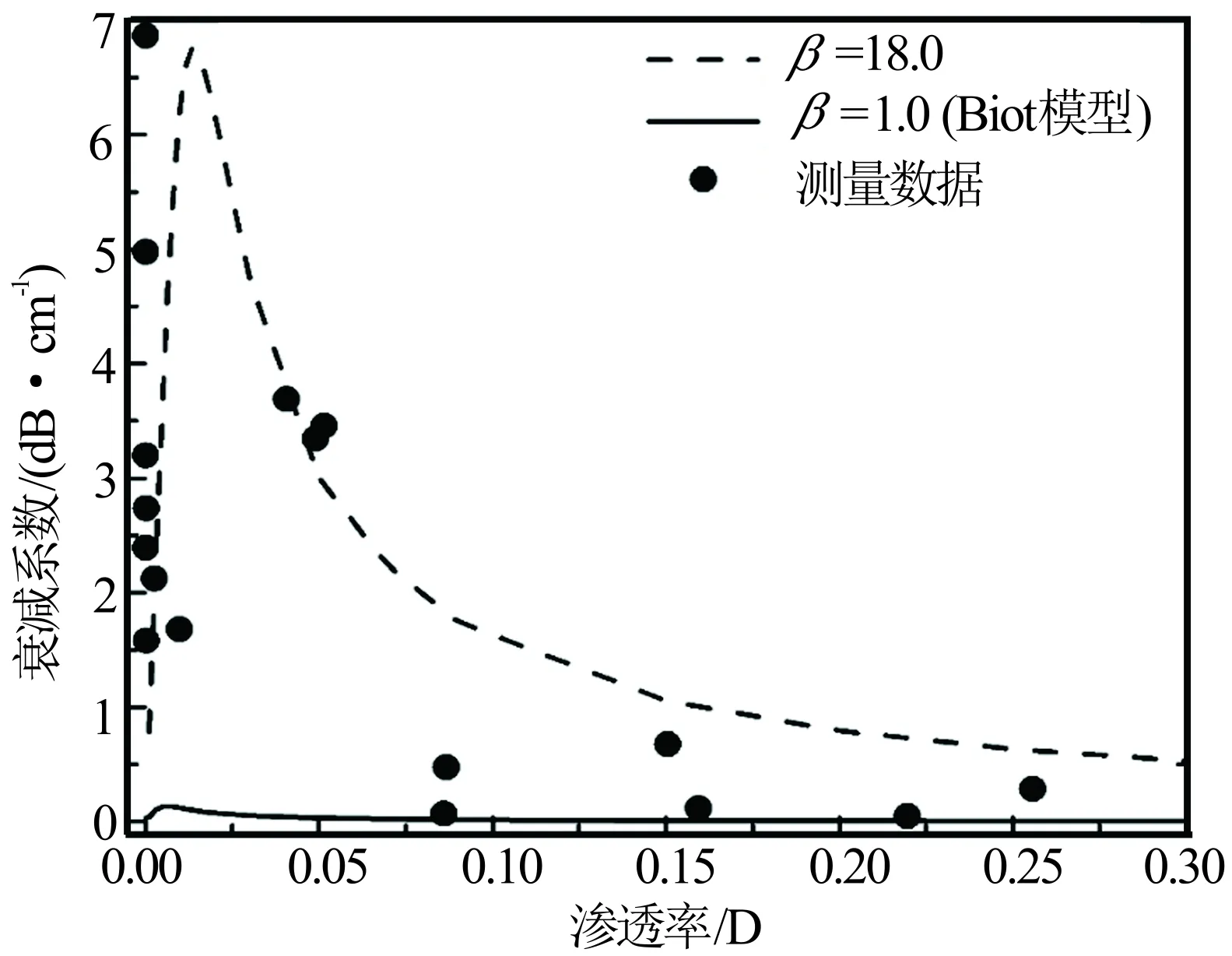
图2 模型计算衰减系数与实验数据[1]对比
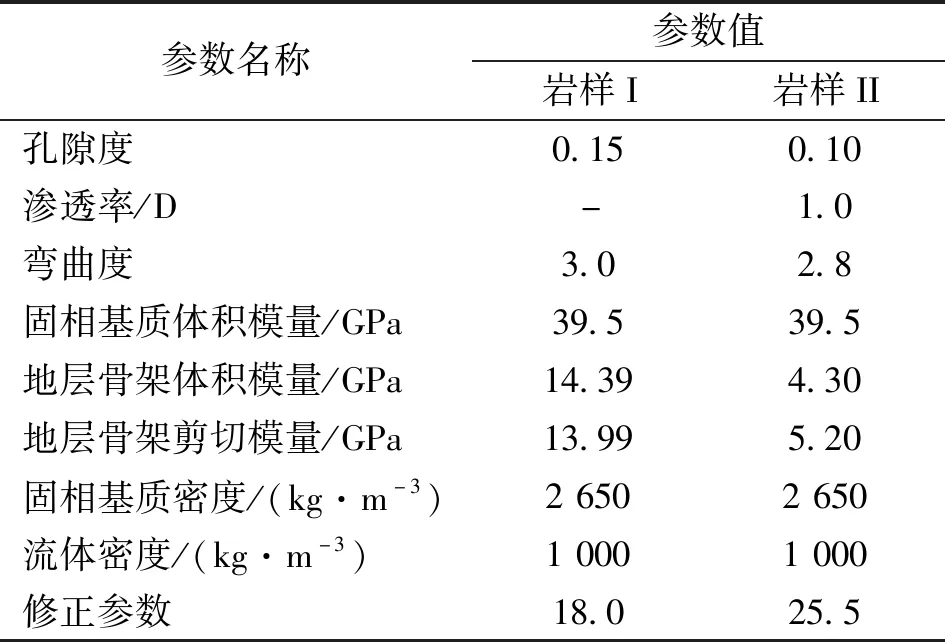
表1 岩样的岩石物理参数
进一步分析实验测量数据与模型计算结果可得:当岩石渗透率较小(小于0.06 D)时,模型取β=18.0的计算结果与实验测量吻合较好;当岩石渗透率较大(大于0.06 D)时,模型取β=18.0计算的岩石的声波衰减高于测量值。在渗透率较大时,为使理论计算结果接近测量结果需要降低β取值。对于同一类岩石,岩石的渗透率一般随孔隙度增加而增加[25],而孔隙度在一定程度上反映岩石骨架的性质。上述结果或从侧面说明β取值不仅受岩石的种类(或构成固相骨架的固体颗粒性质)影响,还受岩石固相骨架结构影响。
图3和图4给出了模型计算结果与另一组实测数据结果的对比。在利用修正模型计算孔隙弹性波速度和品质因子时,采用表1中岩样II的岩石物理参数,用1000/Q(Q为品质因子)随频率的变化来反映频率对声波衰减的影响。图3中实线和虚线分别表示Biot模型和β=25.5时修正模型计算的纵波衰减随频率的变化;图3中矩形框表示不同频率下纵波的1000/Q实测范围[2]。图4中的黑色虚线和红色虚线分别表示β=25.5时修正模型计算的纵波和横波波速随频率的变化,图4中的黑色实线和红色实线分别表示Biot模型计算的纵波和横波波速随频率的变化,图4中的黑色和红色矩形框分别表示不同频率下纵波和横波波速实测范围[2]。

图3 模型计算的1000/Q与实验数据[2]对比(Q为品质因子)

图4 模型计算纵横波速度频散与实验数据[2]对比
比较图3和图4中考虑局部渗透率的修正模型与Biot模型计算的衰减和频散可知,随着局部渗流增加,孔隙弹性波的衰减增加,纵横波的高频极限值和低频极限值的差异也增加。比较修正模型计算结果和实测结果可得:理论计算的品质因子随频率变化趋势也与实测结果一致,且两者在同一数量级;修正模型计算的纵横波波速的频率响应也可有效解释不同频率下实验测量的含液饱和孔隙介质纵横波波速,且理论计算结果在实测结果范围内。与Biot模型计算结果相比,引入修正参数后的理论计算结果更接近实验测量结果。上述结果表明,修正后的Biot模型能够合理解释孔隙介质的波动现象,可通过本修正模型定量预测岩石的波动性质。
3 井孔声场模拟
通过修正模型分析岩石局部渗流(β值)和渗透率变化对井孔声场的影响。这里模拟二维轴对称井眼中的声波压强(简称声压)场,声源为位于井轴上的单极子源,接收器距离声源2.5 m。声源为主频率6 kHz的余弦包络脉冲,脉冲距声源0.01 m处的声压峰值为100 Pa。关于二维轴对称井孔声场的边界条件和声场解析推导过程可参考相关文献[15,18,26]。
图5给出了修正参数β对井孔声场的影响。图5中黑实线、红实线和蓝实线分别为β取1.0、3.0和5.0时的井孔声压计算结果。假定地层的孔隙度为0.2、渗透率为1.0 D。由图5可知,井孔中各个波群的幅值随β值增加而减小,但各个波群的减小幅度不同。随着β增加,斯通利波衰减幅度最明显,其次为横波,最后为纵波。

图5 修正参数β对井孔声场的影响
需要指出地层中的声波衰减与频率有关,衰减峰值对应的频率与地层渗透率有关[22-25]。图6(a)计算了β=5.0时,不同渗透率下的地层衰减的频率响应。如图6(a)所示,纵波1000/Q的峰值对应的频率随渗透率增加而减小。当渗透率为0.1、1.0、10.0 D时,对应的1000/Q峰值频率分别为50.0、5.0、0.5 kHz。即当地层渗透率为1.0 D时,脉冲主频在5.0 kHz附近的测井声波信号的衰减会明显高于其他频段。因此,在采用声波测井数据评价储层渗透率时,需考虑脉冲主频的选择。图6(b)给出了渗透率为0.1、1.0、10.0 D时修正模型计算的井孔声压。比较图6(b)不同渗透率的井孔声压可知,随着渗透率增加,接收到的井孔声压减小,但由于声源主频(6 kHz)接近渗透率为1.0 D时地层的声波衰减峰值频率(5.0 kHz),渗透率为1.0 D时地层的井孔声压略大于渗透率为10.0 D时地层的井孔声压。岩石的渗透率测量实验研究表明,中高渗储层的渗透率一般不高于0.3 D[27]。即对于大多数储层,声波的衰减峰值频率高于5.0 kHz。这说明在利用声波测井数据评价储层渗透率时,声源脉冲主频应小于5.0 kHz,且主频率越低,储层的渗透率评价结果越准确。
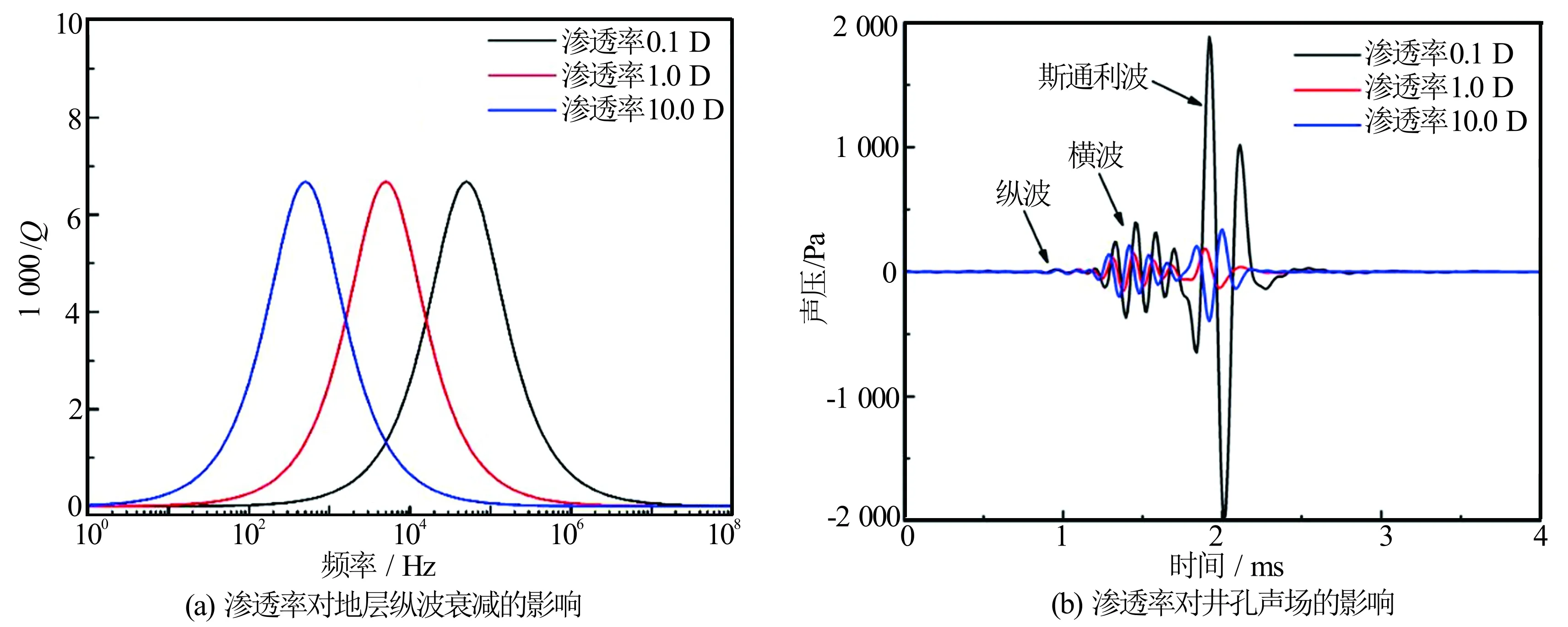
图6 渗透率对声场的影响
4 结 论
文本通过在经典Biot孔隙弹性模型中引入局部渗流效应对经典模型进行了修正,解决了经典Biot模型低估岩石孔隙弹性波衰减的问题。比较了修正模型和经典Biot模型计算的孔隙弹性波衰减和频散,并将两者的计算结果与实测结果进行对比。理论计算与实测数据对比表明:修正模型计算的衰减和频散与实测结果在同一数量级且变化趋势相同,修正模型比经典Biot模型能更合理地解释地层中的孔隙弹性波。最后该修正模型被用于井孔声场模拟,分析局部渗流和渗透率变化对井孔声场的影响。由井孔波场模拟可得:局部渗流和渗透率对井孔声场幅值的影响明显,在利用声波测井评价渗透率时需要考虑局部渗流对井孔声场的影响;采用单极子源声波测井数据进行渗透率反演需要采用较低的声源频率以避开地层中声波的衰减峰值。
