声学/弹性相位梯度超表面设计:原理、功能基元、可调和编码

陈阿丽 汪越胜 王艳锋 周红涛 袁思敏

1 北京交通大学力学系,北京100044

2 天津大学力学系,天津 300350

1 引 言

波传播的调控一直是声波/弹性波领域的关键课题之一.近二十年来,声学/弹性超构材料(Hussein et al.2014,Wang Y F et al.2020,Liao et al.2021) (包括声子晶体(Sigalas &Economou 1992,Kushwaha et al.1993)和超材料(Liu Z Y et al.2000)) 引起了广泛的关注.通过设计具有微结构的功能基元 (或单胞),这类材料可以表现出许多奇特的波动行为,因而在众多领域具有潜在的应用.然而,由于其具有体积大、重量重和损耗强等特点,因而并不便于或适合在现代设备中进行集成和小型化.近年来,超表面受到了人们的广泛关注.超表面也称为超薄膜或单层超材料,通常可分为三类: 折射 (透射) 型超表面、反射型超表面和吸收型超表面(Assouar et al.2018,Liang B et al.2018).超表面由一系列紧密地或稀疏地分布在平面或曲面上的功能基元构成,如图1所示.后面将基本构建单元称为单胞.在紧密排列 (见图1(a)中的插图所示) 的情况下,该单胞即是功能基元本身;而在稀疏排列 (见图1(b)中的插图所示) 的情况下,则包含功能基元和部分基材.反射 (图1(a)) 或折射 (图1(b)) 型超表面可调制波前,其通过引入微结构的逐渐变化而形成沿超表面的相位梯度,因此被称为相位梯度超表面.如果考虑波的吸收而不是波前调制,则称之为吸收超表面.本文将主要关注相位梯度超表面.值得注意的是,半空间表面上的周期性梯度折射率结构可调制沿表面传播的表面波,在一些文献中也称为超表面(Yuan S M et al.2018,Liu T et al.2019,Quan &Alù 2019a,Zeng Y et al.2021).然而,本文则将其视为超材料,因为它在调制波方面具有与超材料相同的机制,因此在本文中不涉及这种情况.

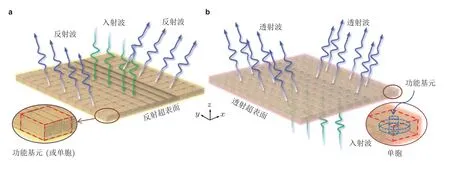
图1 功能基元 (或单胞) 构成的可实现波前调控的相位梯度超表面.(a)反射型,(b)透射型

超表面也可视为具有亚波长厚度的体超材料的二维 (2D) 等效.由于超薄厚度 (亚波长或深亚波长)、低损耗和易于制造/集成等特点,超表面已被证明是用于波动控制的最佳候选者之一.超表面的概念于2011年首次引入电磁波领域(Yu et al.2011,Chen H T et al.2016),然后推广到声学领域(Li Y et al.2013a,Assouar et al.2018).超表面的各种奇特性质 (例如,异常反射和折射、聚焦、波束自加速、声涡旋、散射扩散等) 及在声学成像、扩散、通信、隐身和伪装、振动/噪声控制、能量收集、无损检测、粒子操控、信号模拟计算、信息存储、声学安全等领域的潜在应用已经得到展示.

超表面的成功设计依赖于两个关键步骤.第一是针对波前调制目标获得沿超表面的相移分布.波前调制广泛采用的原理是广义斯涅尔定律 (generalized Snell’s law,GSL) (Yu et al.2011).对于周期性相位调制超表面,格栅衍射理论 (lattice diffraction theory,LDT) 可提高波束定向传输调控的效率(Xie Y B et al.2014).最近提出的表面阻抗理论 (surface impedance theory,SIT)展示出其在设计高效超表面方面的优势(Díaz-Rubio &Tretyakov 2017).第二个关键步骤是设计功能基元的结构,以实现响应波场的可控相移和/或幅值.众所周知,简谐波场是相位的周期函数,其周期为2π (见式 (1) 和式 (2) ),因此,为了实现完整的波前调制,功能基元产生的相移应可通过改变基元结构在2π 周期内调节.到目前为止,人们已经提出了各种各样的功能基元,例如具有卷曲空间的基元、共振基元和复合介质基元等.然而,为了提高波的调制效率,特别是对于水声或弹性波,仍然需要设计新的基元.

近年来,声学/弹性超构材料的可调或可重构引起了人们越来越多的兴趣,以实现对不同频率的自适应、波的实时主动调节以及多种功能之间的切换(Wang Y F et al.2020).通常,主要有两种不同的调节机制.第一种是机械可重构,可以由不同的系统实现,如流/固混合系统、预应力系统、折纸系统和集成元件系统；第二种是基于耦合介质的可重构,可通过使用具有多场耦合效应 (如压电、磁弹性、光力、热弹性等) 的智能材料来实现.根据这些不同的系统,已经设计了各种可重构、可调节、可编程、甚至主动超材料,以实现声波/弹性波的自由调控.更多与该方向相关的信息,请参阅最近的综述文章(Wang Y F et al.2020).然而,仅在五六年前才出现的可调声学/弹性超表面研究仍然非常有限(Chen et al.2017b,Zhao et al.2018,Chen Y Y et al.2018,Zuo et al.2019a,Liu P et al.2020,Yuan et al.2020a),但在电磁场领域则已经相当成熟 (全面而深入) (He et al.2019,Luo et al.2021,Zahra et al.2021).相关的研究正在成为一个热点方向,在功能切换、可调声透镜和二极管、频率选择扩散器、频率自适应斗篷等多功能、超薄宽带可调声波/弹性波器件中具有广阔的应用前景.该方向仍然存在许多具有挑战性的问题,例如可重构性的设计及其机理、可调性实现的策略和方法、编程和反馈控制的实现等.

本文将综述声学和弹性相位梯度超表面的发展.从超表面的设计原理开始,接着是功能基元的设计和波场调制及其潜在的应用.然后介绍了可调超表面,包括可重构基元的设计,以及可调机理和实现.在最后展望部分之前,还介绍了新兴的数字编码超表面(Xie et al.2017b).

2 波场调制与超表面设计原理

不失一般性,简谐声波压力场p(x,t) 的表达式可以写成

简谐弹性波位移场u(x,t) 的表达式为

方程 (1) 和 (2) 表明,可以通过调整幅值P(或U),相位ϕ,和/或极化矢量d来调控声波/弹性波.吸声或隔声超表面用来调节 (通常是降低) 幅值;相位梯度超表面则通过改变相位分布来调制波前.如果相位和幅值可以同时调节,则可设计出实现全息成像的超表面.特别地,对于弹性波,可以设计超表面来调节极化方向从而实现波的模式转换,相应的超表面称为模式转换超表面.

超表面对波场的调制基于惠更斯-菲涅耳原理.即超表面上的每个点都可以被视为次级源,总散射场就等于这些次级源产生的所有波的叠加.考虑图2所示的声学超表面M.忽略时间简谐项,并假设超表面上的幅值和相移分布分别为P(x′) 和ϕ(x′),其中x′为超表面上点的位置矢量.于是,空间任意一点x处的散射 (反射或折射) 压力场由下式给出

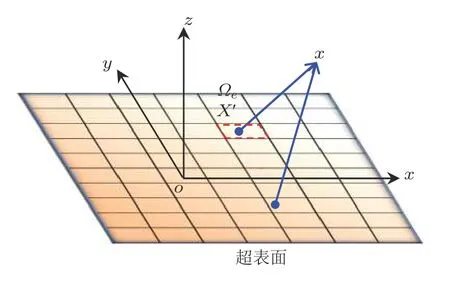
图2 超表面惠更斯-菲涅耳原理示意图

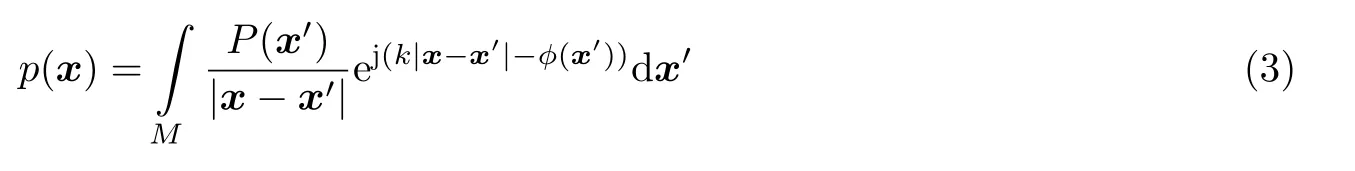
超表面通常被划分为有限的离散单元 (或功能基元).此时,散射压力场可以改写为

其中Ωe表示基元所占有的区域.

惠更斯-菲涅耳原理可用于设计有或没有相位梯度的超表面.然而,对于相位梯度超表面的波前调制,可以以一些简单的设计原理来取代惠更斯-菲涅耳原理.以下将介绍三个常用的原理:广义斯涅尔定律、格栅衍射理论和表面阻抗理论.

2.1 广义斯涅尔定律

众所周知,当界面上不存在相移时,传统的斯涅尔定律确定了反射和折射方向.对于相位梯度超表面,则通过考虑相移的梯度分布建立广义斯涅尔定律,这最早是在电磁场中提出的(Yu et al.2011).

广义斯涅尔定律可以从费马原理推导出来(Aieta,Genevet et al.2012;Aieta,Kabiri et al.2012).这里总结了各种情况下的主要结果.首先考虑最简单的情况,假设一个平直超表面位于xy平面上,并沿x方向呈现相位梯度 (记相位分布函数为ϕ(x) ).如果所有入射波、反射波和折射波均位于xz平面内,且在y方向上均匀 (如图3(a)所示),则控制二维反射/折射波场的广义斯涅尔定律可写为以下形式(Assouar et al.2018,Zhao et al.2018)

其中θi,θt和θr分别为入射角、折射角 (透射角) 和反射角;ki和kt为入射波和折射波的波数(相应的波长为λi/t=2π/ki/t).显然,广义斯涅尔定律 (式 (5) 或 式(6) ) 描述了局部行为.可以通过调整相位梯度来设计局部反射/折射角.从式 (5) 或式 (6) 可以很容易地看出,对于反射,相位梯度应小于4π/λi;对于折射,则应小于2π/λi+ 2π/λt.当ϕ(x) 等于零或常数时,广义斯涅尔定律退化为传统的斯涅尔定律 (如图3(a)中的虚线所示).

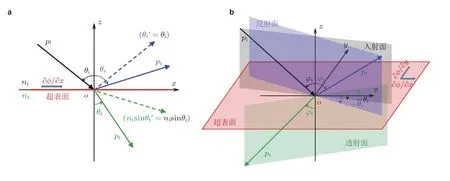
图3 平直超表面的广义斯涅尔定律.(a)二维情况,(b)三维情况

根据目标功能,可由式 (5) 或式 (6) 求得ϕ(x).例如,当垂直入射的平面波以折射角θt转到所要求的方向时,有ϕ(x)=k0(sinθt-sinθi)x+Φ0;当入射平面波聚焦在点(x0,z0)处且k0=ki=kt时,可得其中Φ0对于反射可是任意常数,对于透射则可通过考虑透射率来确定.对于其他功能的ϕ(x) 表达式,例如生成Bessel 波束或自弯曲波束等,可在文献(Chen A L et al.2020) 中找到.

如果xy平面上的超表面在x和y方向上都呈现相位梯度,则一般情况下反射/折射波会位于入射平面之外,如图3(b)所示.此时,控制三维 (3D) 波场的广义斯涅尔定律可写为(Esfahlani et al.2016)

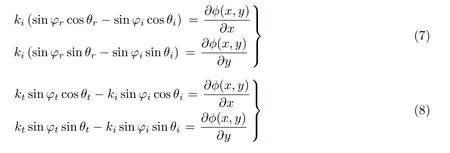
其中θi,θt和θr为相对于x轴的入射、折射和反射角;φi,φt和φr为相对于z轴的方位角;ϕ(x,y)为超表面的相位分布函数.此外,Li X S 等(2019,2020)给出了另一种形式.

对于任意弯曲的超表面z=f(x,y),如图4(a)所示,控制三维波场的广义斯涅尔定律可表示为(Li X S et al.2020)

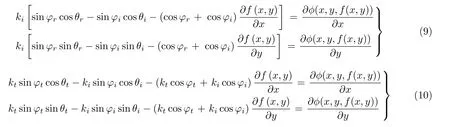
式中,ϕ=ϕ(x,y,f(x,y)) 是超表面的相位分布函数;θi,θt,θr和φi,φt,φr的定义如图3(b)所示.容易理解,在应用广义斯涅尔定律时,超表面的曲率半径应远大于波长.也就是说,上述方程仅对微弯曲的超表面有效.不难看出,对于平直超表面 (即f(x,y)为常数),式 (9) 和式 (10) 分别退化为式 (5) 和式 (6).

对于如图4(b)所示的二维弯曲超表面z=f(x),可以由方程 (9) 和方程 (10) 直接得到控制xz平面内二维波场的广义斯涅尔定律(Fan et al.2020b)

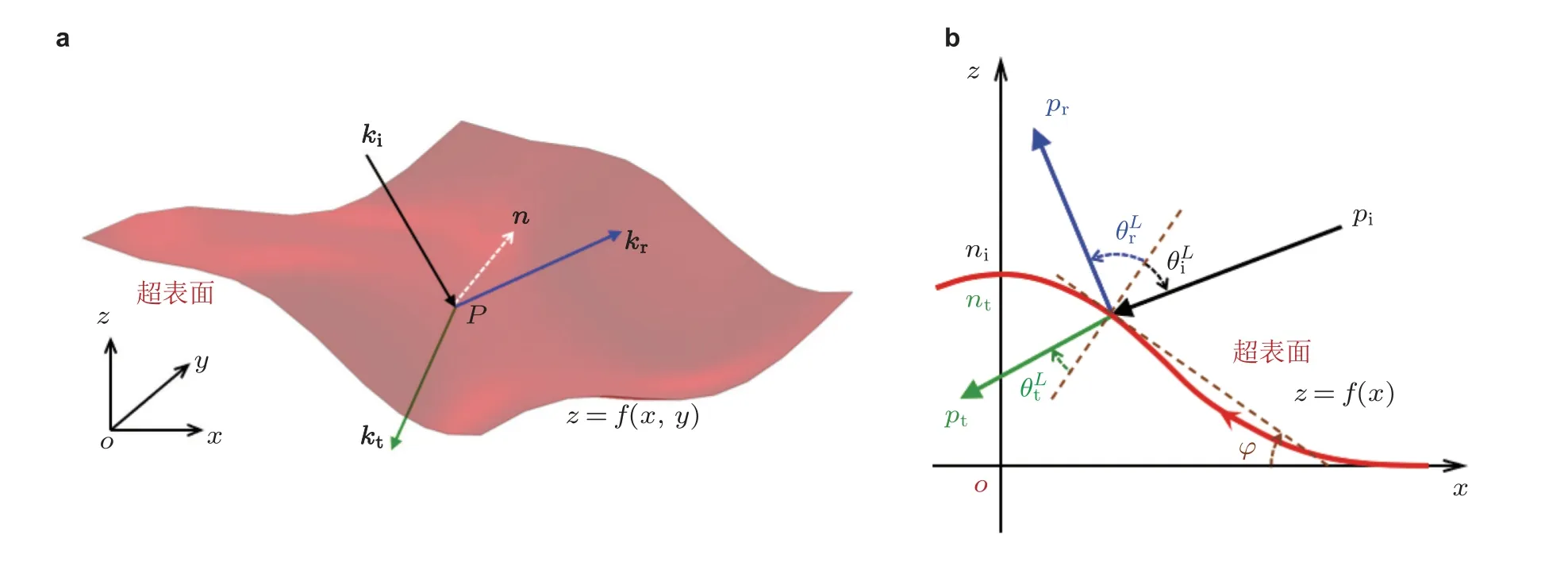
图4 曲面超表面的广义斯涅尔定律.(a)三维情况,(b)二维情况

在局部坐标系中,上式可以写为

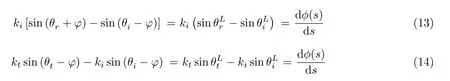
其中θiL=θi-φ,θtL=θt-φ,θrL=θr+φ.

广义斯涅尔定律为相位梯度超表面提供了一种简单的设计方法.结合超表面的形状函数、入射波前和目标反射/折射波前,广义斯涅尔定律可以给出所需的相位分布,其设计过程如图5所示.基于广义斯涅尔定律的设计属于局部设计或独立设计.只需要单独设计每个基元,以获得特定的相位延迟;然后根据所需功能将相位延迟能够覆盖整个2π 周期的一系列基元组装起来,形成具有特定相位分布的超表面.超表面的尺度应满足一定要求: 其厚度是波长的几分之一,基元的尺寸应该明显小于波长.广义斯涅尔定律非常简单,已广泛应用于超表面的设计.然而,设计的超表面可能会产生高阶寄生衍射(Tang et al.2014,Cao et al.2018b),这使得部分反射/折射能量沿非预期的方向传播,导致波调控效率降低.其他理论,如格栅衍射理论和表面阻抗理论,可以解决该问题.

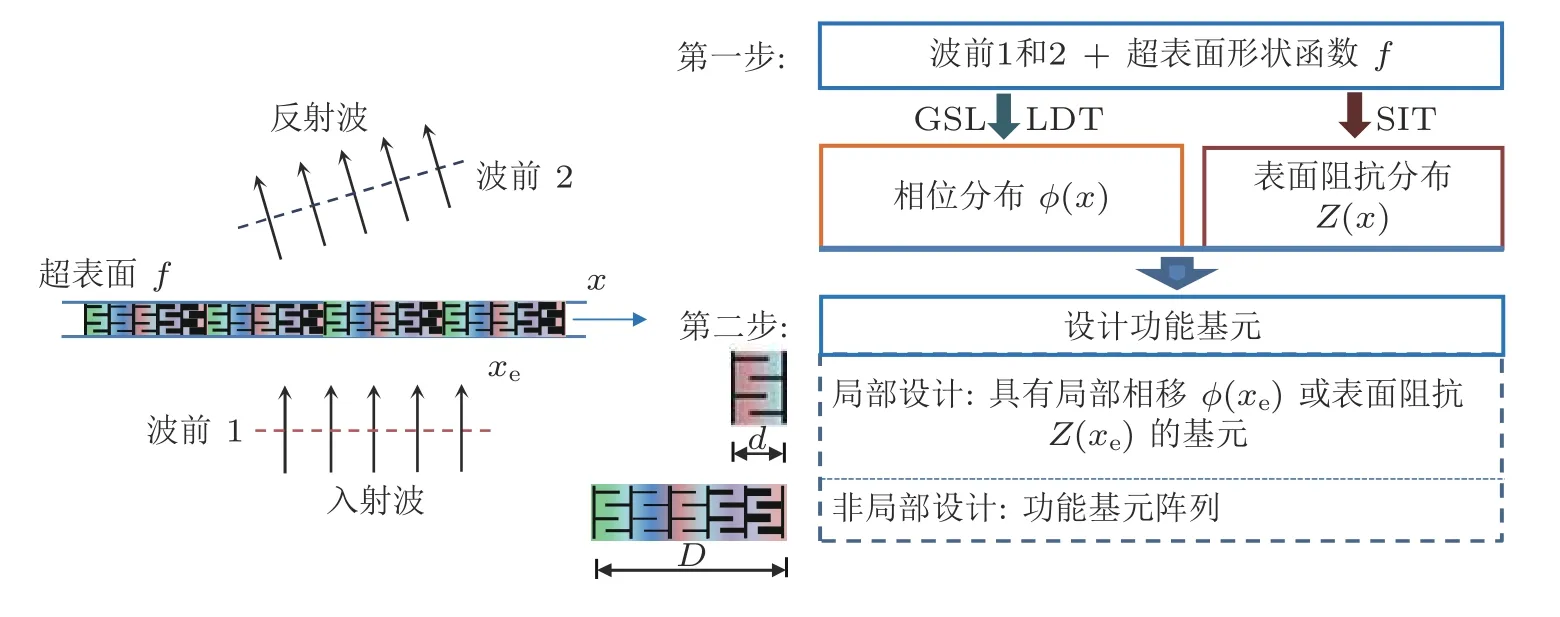
图5 超表面设计流程

2.2 格栅衍射理论

众所周知,对于周期结构中传播的波,其幅值和/或相位受到周期性的调制.当结构周期与波长相当时,衍射很强.相关的衍射理论已应用于光栅或声栅的设计,也被用来设计超表面 (通常称为超格栅),其周期性排布的构筑单元 (或称为超胞) 是一个非均匀基元阵列(Xie Y B et al.2014,Wang W Q et al.2016).这样设计的超表面通常在与结构周期相当的波长下工作,因此可视为声子晶体(Xie Y B et al.2014).在这种情况下,周期性带来的非局部效应将在波传播中发挥关键作用,而广义斯涅尔定律将变得依赖于波矢,用于波调制效果不佳(Xie Y B et al.2014).若将波场写为Floquet-Bloch 形式,则可以得到以下控制二维反射和折射波前的格栅衍射理论 (详见文献(Wang W Q et al.2016))

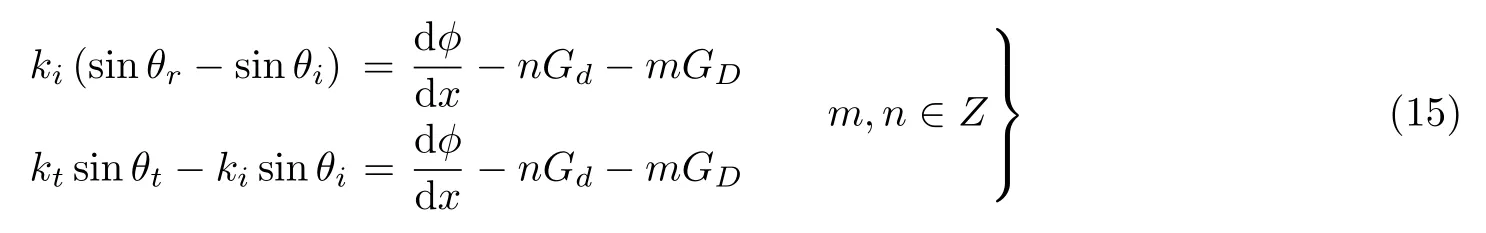
其中沿超表面 (假定为平直的) 的相位梯度为常数.上式考虑了高阶衍射波.Gd=2π/d和GD=2π/D是倒格矢的模,d为功能基元的宽度,D为构筑单元 (基元阵列) 的周期 (长度),如图5所示.如果只考虑 (m,n)=0 项,则上式退化为广义斯涅尔定律即式 (5) 和式 (6).

另外,每个构筑单元的相位延迟必须至少覆盖一个完整的2π 范围.如果覆盖2lπ 范围,其中l为正整数,则可得如下恒定相位梯度

如果基元宽度明显小于波长,则基元的周期效应可以忽略.此时,结合式 (16),式 (15) 可简化为

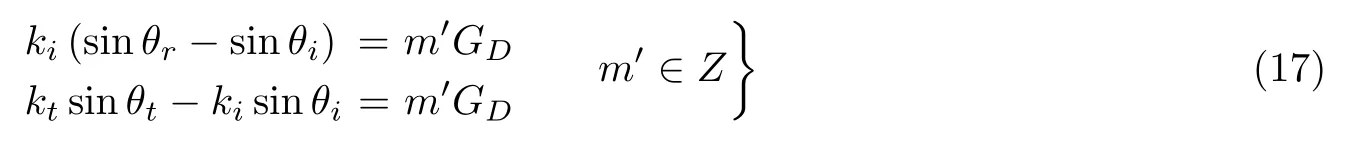
值得注意的是,当m′=0 时,式 (17) 简化为传统的斯涅尔定律;当m′=1 时简化为广义斯涅尔定律.

基于格栅衍射理论的超表面设计本质上是一种非局部设计或协同设计.与广义斯涅尔定律不同的是,利用格栅衍射理论可以设计超表面获得不同阶数或不同方向的衍射波.尤其对于大角度反射/折射情况,可以实现高质量和高效率调控,因为功率流会沿表面重新分布并保持守恒(Wang W Q et al.2016,Fang et al.2017,Hou et al.2019).然而,这一理论也有其局限性.例如,如果要完全抑制非预设方向或阶数的散射波,则需要对构筑单元中的所有基元同时进行协同设计,这无疑增加了设计的困难.因此,通常要利用优化方法精心设计整个构筑单元的构型(Zhou et al.2021a).此外,除了异常反射/折射外,其他波前调制 (例如聚焦、波束弯曲等) 很难通过格栅衍射理论实现(Chiang et al.2021).格栅衍射理论的其他局限包括带宽窄、平直超表面假设等.需要指出的是,当结构相对于波的入射方向不对称时,对于没有相位梯度的周期性结构,也可以利用格栅衍射理论设计实现异常反射/折射(Bernard et al.2022).

2.3 表面阻抗理论

如上所述,寄生衍射可能出现在由基于广义斯涅尔定律设计的超表面调制的响应场中,尤其是对于大反射/折射角的情况.这是因为与格栅衍射理论不同,广义斯涅尔定律不考虑其他衍射阶数 (见式 (15) ),因此,基于广义斯涅尔定律的超表面不一定能抑制这些不需要的阶数.为了克服这一局限,Zhao 等(2013a,2013b)提出了一种阻抗控制的广义斯涅尔定律,用不均匀的表面阻抗代替相位分布设计反射超表面,并在数值上实现了波的异常反射和聚焦.Díaz-Rubio 和Tretyakov(2017)及其合作者(Díaz-Rubio et al.2017,Asadchy et al.2016)针对异常反射和折射系统地发展了基于表面阻抗理论的超表面设计原理。他们首先考虑了电磁波(Asadchy et al.2016,Díaz-Rubio et al.2017),然后扩展到声波(Díaz-Rubio &Tretyakov 2017).

2.3.1 异常反射

在基于广义斯涅尔定律的无损反射超表面的局部设计中,通常可以仔细地设计功能基元以产生具有单位局部反射系数的所需相移.遗憾的是,当将如此设计的基元组装成超表面时,所需反射方向上的反射功率系数小于1,并且随着反射角的增大而减小.也就是说,并非所有的能量都被重新定向到所需的方向,这就导致了寄生散射(Díaz-Rubio &Tretyakov 2017).在反射角很大的情况下,寄生散射变得非常显著.Díaz-Rubio 和Tretyakov(2017)利用表面阻抗解释了这一现象.他们发现,对应于广义斯涅尔定律的表面阻抗是纯虚数,这意味着没有能量流入或流出超表面.因此,不能流入所预设方向的部分能量必将散射到其他非预设的方向.

为了减小寄生散射,提高反射效率,Díaz-Rubio 和Tretyakov(2017)发展了表面阻抗理论.假设角度为θi的入射波在超表面 (y=0) 上以角度θr反射,则由Zs=ptot(x,0)/(-n·vtot(x,0)) [其中ptot(x,0) 为总压力场分布,vtot(x,0) 为相应的总速度分布]定义的表面阻抗可表示为(Díaz-Rubio &Tretyakov 2017,Zhu &Lau 2019b)

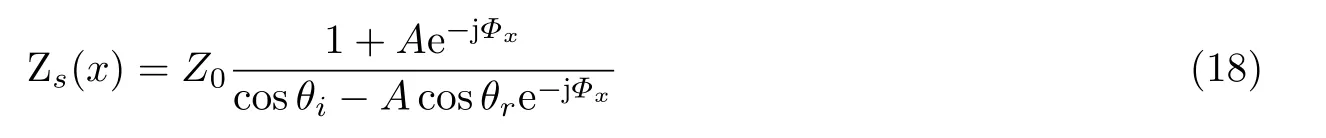
式中A为反射压力幅值与入射压力幅值之比;Φx=k(sinθr-sinθi)x为相移;Z0=cρ为背景介质的特征阻抗.方程 (18) 可用于设计超表面.为此,由R(x)=(Zs-Zi)/(Zs+Zi)≜r(x)ejΦr(x)(其中Zi=Z0/cosθi) 计算局部反射系数,然后,独立设计基元使其反射幅值和相位分别与r(x)和Φr(x)相匹配,这通常要利用优化方法来实现.

注意,这样得到的表面阻抗是复数.如果要求A=1 (即入射场和反射场的压力幅值相同),则当θi＜θr时,阻抗的实部在整个超表面上取正值 (Re(Zs)＞0 ),意味着能流将被超表面吸收(Díaz-Rubio &Tretyakov 2017).因此,应引入有损基元来设计超表面,这可以通过引入一些能量耗散机制 (如热黏度) 或使用耗散材料 (如橡胶或泡沫) 来实现(Zhu &Lau 2019b).另一方面,当θi＞θr时,有Re(Zs)＜0,意味着必须向系统输入额外的能量,以确保A=1(Díaz-Rubio &Tretyakov 2017).因此,需通过引入供能设施 (如压电系统) 设计有源 (或增益) 基元,这通常非常困难不易实现.

基于上述设计的超表面可以消除寄生散射,但存在功效低的缺点,尤其是对于很大的反射角.如果需要将所有输入能量反射到所预设的方向,则必须确保反射功率系数η=A2cosθr/cosθi=1(Díaz-Rubio &Tretyakov 2017).此时,必须允许穿过超表面和反射域之间的界面上有能流交换,但沿超表面横向的能流必须守恒,这样,整个超表面能流守恒,而基元的局部能流不守恒.这意味着在一个周期内必须同时存在有损基元和有源基元,会使设计变得非常困难.目前已提出了若干方法克服这一困难.例如,Díaz-Rubio 等(2019)利用常规被动基元设计了一个能流共形超表面,其切线方向与宏观声场的能流方向一致,以避免能量流出或流入超表面.Quan 和Alú(2019b)设计了一种非局部基元来构造被动超表面.这些基元相互连接,允许之间的能量流动并保持能量守恒.也可通过在一个周期内协同设计所有基元来构建非局部超表面,以倏逝波作为引导能量的一种机制来保持能流平衡(Díaz-Rubio &Tretyakov 2017).协同设计一般采用优化方法来实现.

2.3.2 异常折射

对于折射型声学超表面,通常定义一个阻抗矩阵 (一个2×2 的矩阵,记为Z) 联系超表面两侧的压力场和速度场(Díaz-Rubio &Tretyakov 2017).对于基于广义斯涅尔定律设计的超表面,Z的所有元素都是纯虚数;主对角线元素相同 (即Z11=Z22).这意味着无损设计是可能的,且基元是对称的.然而,如前所述,这样设计的超表面可能会出现寄生散射,导致功效降低,尤其是对于大折射角的情况.可以证明,如果想得到单位折射功率系数,则必须有Z11≠Z22.也就是说,需要不对称或双各向异性基元来实现对透射波的完全控制(Díaz-Rubio &Tretyakov 2017,Li J F et al.2018).在这种情况下,Z是纯虚的,双各向异性基元在理论上可以是被动的和无损的,同时可获得大于单位1 的压力透射系数,从而可抑制非预设方向的衍射波(Díaz-Rubio &Tretyakov 2017,Li J F et al.2018,Peng et al.2021).

双各向异性超表面设计适用于平面波,但由于法向能流不守恒,所以对更复杂的波前调控(如聚焦、波束分裂/弯曲、全息等) 效果不佳(Li J F et al.2020,Peng et al.2021).为了避免设计有损/增益基元以沿超表面进行局部能量的再分配这一困难,Peng 等(2021)提出了一种能流共形双各向异性超表面,以实现对任意声波波前的高效操控.超表面的形状通过在超表面局部施加相等的入射和透射能流来确定 (即使入射和透射声强场的法向分量相同) (Peng et al.2021).Li J F 等(2020)提出了另一种方法,他们将自诱导表面波纳入散射场,以满足局部能流守恒的要求,并设计了双各向异性声学超表面,以实现近乎完美的任意波束分裂和异常折射.他们发现了一种违反直觉的现象,即通过允许受控的透射/反射场,可以获得完美的反射/透射.事实上,他们的研究提供了一种同时控制反射和透射的新思路.

表面阻抗理论提供了一种设计高效超表面的新工具.然而,还需要克服一些限制.例如,对于简单的情况,如平面波波前转向,设计很容易实现;而对于复杂的波前调制,推导适当的表面阻抗分布并实现基元的优化设计则并非易事(Li J F et al.2019,Song et al.2019,Peng et al.2021,Xie &Hou 2021).此外,基于该理论的超表面宽频设计也具有挑战性.

3 功能基元设计

基于上述原理,可以设计出具有不同功能的相位梯度超表面,设计过程如图5所示.超表面通常由离散的功能基元组成,功能基元的微观结构逐渐变化,进而形成梯度相移和/或幅值.因此,基元设计是实现超表面功能的关键步骤之一,本节将对此进行综述.

通过分析局部波场进行基元设计,是一种简单而灵活的方法.该方法假设简谐波入射到单胞上,然后计算其反射或透射响应.其中计算可以通过解析或数值实现,使用较广泛的方法是有限元法.通常选择如图6所示的柱状区域作为计算模型,该区域包含单胞和波传播介质.在左侧部分 (入射区域) 施加均匀平面波作为背景波场,或在激发平面上施加均匀分布的波源 (压力、位移或应力) 以产生入射平面波.透射波或反射波的信息,包括相位、幅值等,可通过将信号接收平面上的值进行平均 (或直接记录中心点的值) 获得.信号接收平面设置在距离单胞一定距离处(约一个波长或更远),以避免近场散射的影响.计算模型侧面施加周期边界条件;两端施加辐射条件或低反射边界条件以消除反射.对于空气声,由于空气和固体材料之间存在较大的阻抗失配,因此可以将固体结构视为声学硬边界,侧面的周期条件也可以用声学硬边界条件代替(Fan S W et al.2019).

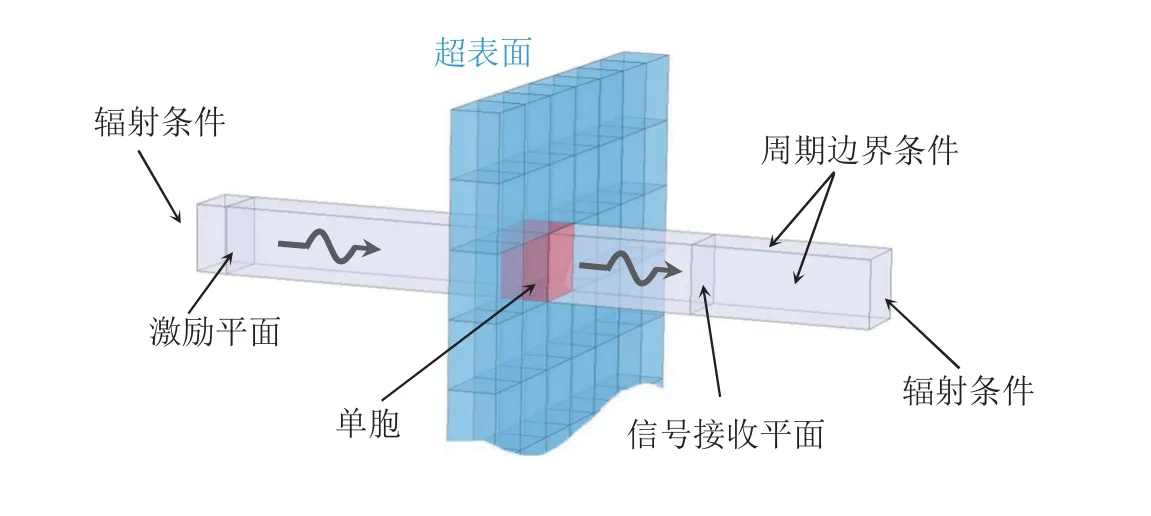
图6 单胞计算模型 (透射)

功能基元的设计应使其在改变几何或材料参数时,能够提供2π 相移和/或0 到1 的反射/折射系数.波通过基元时的相移可以很容易地通过ωL/c估算,其中ω是角频率,L是波在基元中的传播路径长度.因此,可以通过分别改变L和c或同时改变两者来实现相位调制.到目前为止,基于这些机制,已经提出了许多基元,包括但不限于: 空间卷曲结构、共振结构、复合介质结构等.通常,空间卷曲结构基于对波通道长度 (L) 的调节;而共振结构或复合介质结构依赖于对波速 (c) 的调节.除了纯相位调制外,在某些情况下,特别是当需要精确地调控波场时,例如全息成像、粒子操纵等,可能需要同时进行相位和幅值调制.接下来,总结用于调控空气声、水声和弹性波的若干典型功能基元设计.

3.1 空气声功能基元

空气声是一种标量波.空气和固体之间的声学失配通常很大,因此可以忽略流固相互作用.所有这些因素使得空气声功能基元的设计变得更简单.最典型的空气声功能基元是空间卷曲基元和共振基元.

3.1.1 空间卷曲基元

空间卷曲基元包含一个锯齿形或卷曲的声通道.当声音通过延长的通道时,产生相位积累.2012年,Liang 和Li(2012)首先提出了图7(a)所示的空间卷曲结构并将其作为构建声学超材料的基元,以此构建的声学超材料表现出极端的有效参数,包括双负参数、近零密度和大折射率.他们还发现,可以通过改变通道长度来调整有效参数.现在也称这种结构为锯齿形或迷宫式结构,Li 等(2012)和Peng 等(2014)随后使用此结构设计了梯度折射率声透镜.从现在的观点来看,他们设计的这种声透镜实际上是一种超表面.通过调整基元尺寸,可以获得梯度变化的有效折射率和阻抗.如图7(b)所示,不同的声通道长度会导致相位梯度,因此可以调制波前.通过将上述结构旋转拉伸为圆形结构 (图8(a)),Li 等(2015b)设计了一种三维超薄平面透镜.事实上,锯齿形路径延迟了声波的传播,因此可以通过改变通道长度来调整声波相位.当通道长度约为半波长的整数倍时,可以实现法布里-珀罗共振,产生极高的透过率;甚至可以在特定的入射角 (即光学中的布鲁斯特角) 下获得宽频完全透射(Li et al.2013b).Tang 等(2014)提出改变卷曲结构内隔板的数量和长度,来获得整个2π 周期内的相移.与Li 等(2012,2015b)不同的是,他们将两个相邻的基元紧密排列在一起构建超表面,中间没有空气缝隙,实现了高效的声束转向.几乎同时,Xie Y B 等(2014)提出了锥形迷宫基元,如图8(b)所示,并通过设计的具有双层基元的超表面实现了波束转向和行波-凋落波的模式转换.其中卷曲通道的圈数变化可以产生覆盖整个2π 周期范围的不同相移;而大开口截面梯度变化的锥形卷曲通道可以提供更好的阻抗匹配,这有利于实现高效传输.许多已发表的研究中都使用了类似的基元来设计高透射率超表面,如Liu 等(2017a)基于格栅衍射理论获得了全角度的负折射,Zuo 等(2017,2018b)数值实现了声学模拟计算,文中均使用了类似基元结构.

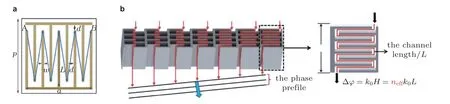
图7 (a)透射型空间卷曲基元(Li et al.2012),(b)通过改变声通道长度实现波前调控(Zhao et al.2018)

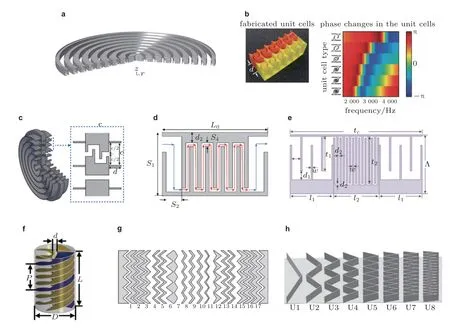
图8 透射型空间卷曲基元.(a)环形锯齿结构(Li et al.2015b),(b)锥形空间卷曲结构(Xie Y B et al.2014),(c)空腔共振增强的锯齿结构(Molerón et al.2014),(d)具有阻抗匹配层的锯齿结构(Jia Z T et al.2018),(e)类三明治锯齿结构(Zuo et al.2018a),(f)带螺旋通道的螺旋结构(Zhu X F et al.2016),(g)由锯齿狭缝组成的超表面(Tang et al.2015),(h)V 形刚性薄板形成的超表面基元(Lan et al.2017a)

提高阻抗匹配是透射超表面设计中应考虑的一个关键问题,Xie Y B 等(2014)和Memoli 等(2016)提出的声通道梯度设计是解决方案之一.在图7(a)所示结构的基础上,一些学者们也设计了锥形或喇叭状基元(Memoli et al.2016,Ghaffarivardavagh et al.2018)以实现高效传输.Molerón 等(2014)在环形空间卷曲基元上添加了同心环 (如图8(c)所示) 来设计基于超表面的圆形平面透镜,该透镜可以产生具有极高放大率的锐聚焦.其中的同心环诱发空腔共振,再加上法布里-珀罗共振,导致了显著的放大增强效应(Molerón et al.2014).如图8(d)所示,Jia Z T等(2018)在一个空间卷曲结构的两端引入了阻抗匹配层 (宽Z 形通道),通过修改其几何结构,可以获得宽频域的高效传输.事实上,上述结构相当于具有阶梯截面的管道(Jia Z T et al.2018),可用于各种场景,例如,将平面波转换为瓶状波束(Chen et al.2018d)或涡旋波(Jia Y R et al.2018)等.由通道尺寸不同的多个迷宫结构组成的多层空间卷曲基元 (如图8(e)所示的三明治结构),经过精确设计可满足完美的阻抗匹配,也能够产生高效的透射(Zuo et al.2018a,Ju et al.2018,Tang W P et al.2019).图8(d)和图8(e)所示的两种结构都具有锥形截面的声通道,这有助于增强阻抗匹配和提高透射效率.Tang 和Ren (2017)指出,通过简单地调节空间卷曲基元的两个几何参数可以改变其有效折射率,进而提高阻抗匹配.此外,用不同材料填充通道也可以实现匹配的阻抗(Jahdali &Wu 2016),尽管在实践中可能不易找到合适的材料.

声通道也可以在三维空间中卷曲,此类基元的一个典型实例是具有螺旋声通道的螺旋结构,如图8(f)所示,Zhu X F 等(2016)利用此基元构建了可以产生自加速波束的超表面.其中的有效折射率和动态质量密度随结构螺旋度的变化而变化,因此可以实现相位梯度设计.如果引入具有梯度螺旋度的阻抗层则可以进一步改善阻抗匹配并产生宽频高效传输(Ding et al.2017).由固定在圆柱管内的扭带形成的空间卷曲基元,由于通道较宽,也可以获得较高的传输率(Esfahlani et al.2017).Liang 等(2020)利用具有螺旋声通道的同心圆分层基元来设计超表面,实现了轴对称聚焦.其中为了提高传输效率,采用了梯度阻抗设计.还有一些其他的变异空间卷曲基元,如图8(g)所示的由锯齿形狭缝形成的结构(Tang et al.2015),或图8(h)所示的由V 形刚性薄板形成的结构(Lan et al.2017a),后者被证明具有宽频响应的优势.

通过在一端引入刚性面,可以很容易地将上述透射基元转变为用于构建反射超表面的功能基元.图9(a)和图9(b)分别显示了与图7(a)和图8(b)结构对应的反射基元(Li Y et al.2013a,Wang W Q et al.2016).它们已被用于设计反射型超表面实现波束转向和聚焦(Li et al.2014,Liu et al.2017b)、能量收集(Qi &Assouar 2017,Qi et al.2017)、地毯隐身(Wang et al.2017)(即观察者将物理系统视为具有平坦地面的虚拟系统(Li &Pendry 2008)) 等.除了空间卷曲基元外,还可以使用直井基元 (末端封闭) 来设计声学超表面,如图9(c)所示(Zhu et al.2015a),这类超表面也被称为梳状超表面.不同的直井深度意味着声波传播路径的长度不同,因此会导致不同的相移.这种基元已用于设计反射超表面实现各种声束调制功能(Zhu et al.2015a,Zhu Y F et al.2016,Shen C et al.2018,Song et al.2019).直井基元的优点之一是可以获得反射波场的解析表达式.

图9 反射型空间卷曲基元.(a)具有锯齿形通道的结构 (Li Y et al.2013a),(b)锥形迷宫结构 (Wang W Q et al.2016),(c)类直井基元构成的梳状超表面 (Zhu et al.2015a)

3.1.2 共振基元

与空间卷曲基元不同,共振基元通过各种不同的共振机制 (如亥姆霍兹共振、薄膜共振和混合共振) 减缓波的传播,从而调节相位和/或传输系数.Li 等(2015a)提出了一种共振基元,该基元由连接至直通道的亥姆霍兹共振腔 (Helmholtz resonators,HRs) 串联组成,如图10(a)所示.调整通道高度 (图中h1,其中h值固定) 可以改变波速,从而使透射相位在0 到2π 之间变化.考虑到法布里-珀罗共振条件,将直通道长度 (w,即超表面厚度) 设计为半波长,可以提高阻抗匹配和透射效率.关于其中的亥姆霍兹和法布里-珀罗混合共振的声学理论和物理机制详见文献(Li et al.2016).Lan 等(2017b)对这种混合共振基元的有效声速梯度分布进行了理论分析.该基元通过中心旋转操作可以扩展到具有径向相位梯度的轴对称结构,以实现三维准直自加速声束(图10(b)) (Li &Assouar 2015);或者扩展到具有周向相位梯度的圆柱形结构,以生成涡旋声波(图10(c)) (Jiang et al.2016a).Han 等(2018)提出了另外一种亥姆霍兹共振腔的串联形式 (如图10(d)所示) 来构建超表面,实现了折射波的波束转向.Dong 等(2020)通过连续放置两个双开口球形亥姆霍兹共振腔构建了一个哑铃形共振基元 (图10(e)).Zhai 等(2015)设计了图10(f)所示的薄膜型基元,它是一个充气的矩形空腔,两端用张紧的弹性膜密封,可以通过改变膜的厚度来调节相位.Lan 等(2018)提出了由四个谐振器连接到直通道构成的薄膜型混合基元 (见图10(g)) 来构建超表面,每个谐振器都是一个充满空气的刚性背腔,上端用薄膜密封.该结构类似于图10(a)所示的亥姆霍兹共振基元,薄膜对应于亥姆霍兹共振腔的开口.结果显示,薄膜基元有助于设计尺寸较小的超表面.

与反射空间卷曲基元类似,可以通过在相应透射基元的一端增加刚性面来获得反射共振基元.例如,Shen 和Cummer(2018)对图10(a)中所示的基元进行改进,提出了利用多重内反射实现具有高吸声率的反射型梯度超表面的设计策略.Liu 等(2016)提出了一种带有管状共振器 (而非亥姆霍兹共振腔) 的基元,来设计可实现全角度负反射的超表面.另外一类非常简单的反射基元是开口面向入射波的亥姆霍兹共振腔,如图11(a)和图11(b)所示.可以通过改变其开口(Ding et al.2015,Wang et al.2016b,Dubois et al.2017,Zhu et al.2017,Zhao et al.2020)或空腔(Faure et al.2016,Li Y et al.2019,Zhu &Assouar 2019a,Weng et al.2021)的尺寸来调节反射波的相位.此类基元的一个优点是可以构造超薄超表面 (薄至二十分之一波长或更薄) (Zhu et al.2017,Dubois et al.2017,Zhao et al.2020).Li X S 等(2019)提出了一种反射基元,基元由多个亥姆霍兹共振腔串联而成,可调的水面作为刚性反射面 (参见图11(c)中的左图).同时采用内孔孔径的梯度设计 (见图11(c)中的右图),以提高阻抗匹配和入射面外的波反射效率.Zhou H T 等(2020)利用基于遗传算法的参数优化方法,构建了具有叠层亥姆霍兹共振基元的被动声学超表面,实现了超宽频广角地毯隐身.薄膜封口的刚性背箱或空腔 (如图11(d)所示) 可用作基元来设计反射超表面(Esfahlani et al.2016;Zhai et al.2016;Chen 2017a,2018).调节膜的尺寸(厚度(Esfahlani et al.2016)或宽度(Zhai et al.2016,Chen 2018)) 或张力(Chen 2017a)可以产生适当的相移,并覆盖整个2π 范围.粘贴在膜上的质量 (如图11(e)所示(Chen 2017a)) 可以增强共振.由薄膜型基元构成的反射超表面通常较轻,且厚度为深亚波长.类似的基元 (板状或壳状基元) 可以由板或壳而不是薄膜构成,例如Ma F Y 等(2018,2019a,2019b)设计了双层板状 (见图11(f)) 和壳状基元,以构建基于超表面的地毯斗篷.

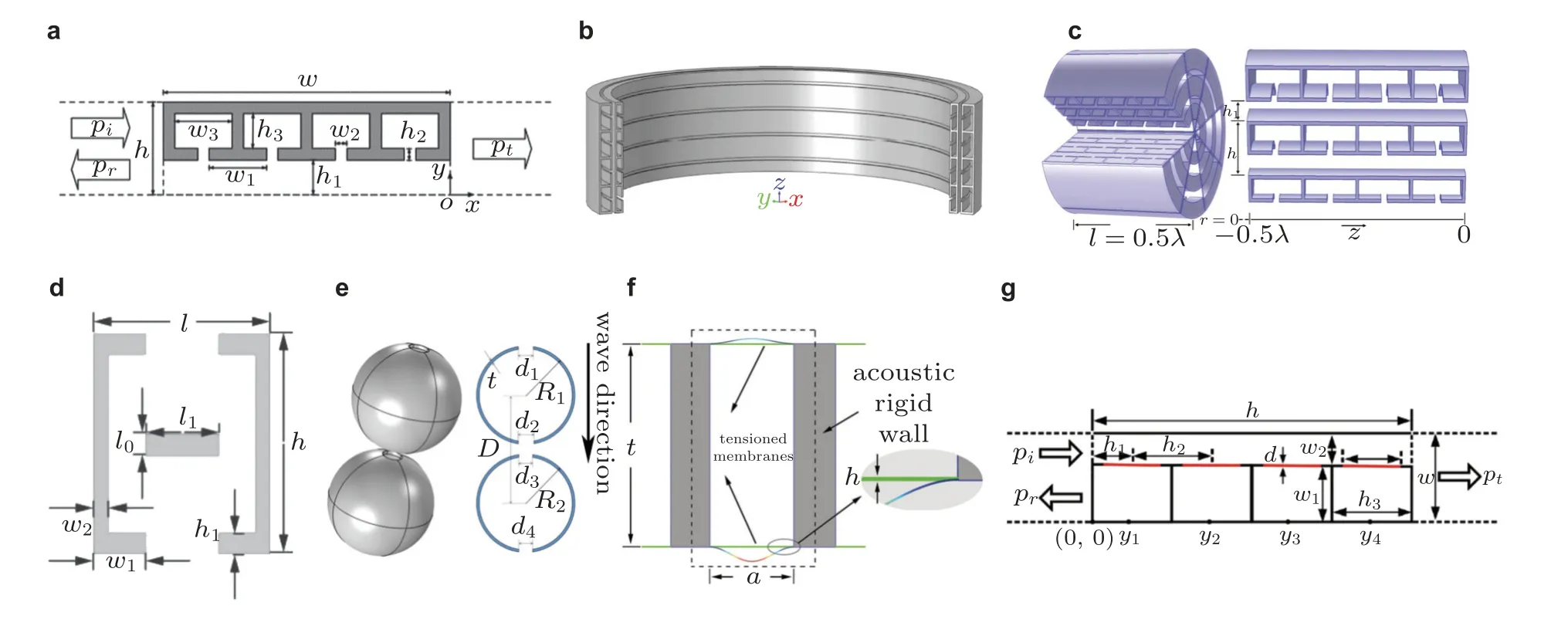
图10 透射型共振基元.(a)由连接至直通道的亥姆霍兹共振腔串联组成的结构(Li et al.2015a),(b)用以实现三维准直自加速声束的具有径向相位梯度的轴对称结构(Li &Assouar 2015),(c)用以生成涡旋波的具有周向相位梯度的圆柱形结构 (Jiang et al.2016a),(d)亥姆霍兹共振腔串联结构(Han et al.2018),(e)哑铃形共振基元(Dong et al.2020),(f)薄膜型基元(Zhai et al.2015),(g)薄膜型混合基元(Lan et al.2018)

图11 反射型共振基元.(a)亥姆霍兹共振基元(Ding et al.2015),(b)管状共振器(Zhu &Assouar 2019a),(c)无梯度设计 (左图) 和有梯度设计 (右图) 的亥姆霍兹共振腔串联基元(Li X S et al.2019),(d)具有刚性背箱的薄膜型基元(Zhai et al.2016),(e)带有附加质量的薄膜型基元(Chen et al.2017a),(f)双层板状基元((Ma F Y et al.2018)

除了上述空间卷曲和共振基元外,用复合介质填充声通道也可用于设计功能基元.通过调整不同组分的体积,可以调整相移和阻抗匹配.Mei 和Wu (2014)通过在刚性薄板上切割周期性直通式狭缝阵列并充满不同气体 (空气/氩气/氙气),设计了一种声学超表面,实现了高效可控的透射和全反射.文献(Su &Ko 2022)中的声波分裂和捕获、文献(Wang et al.2016c)中的单向隐身以及文献(Wang et al.2016a)和(Song et al.2019b)中的非对称传输均采用了相同的设计方法来构建超表面.一般来说,由于很难控制界面附近不同气体或液体的扩散,这种设计策略实际上很难实现.

几乎所有上述基元的设计均未考虑空气与结构的相互作用;少数的研究考虑了损耗的影响.损耗通常源于材料的黏性以及由壁面摩擦和热黏性扩散引起的热黏性.Molerón 等(2016)和Jiang 等(2017)分别针对图7(a)所示的空间卷曲基元和图10(a)所示的混合共振基元详细讨论了热黏性效应.Gerard 等(2018)系统分析了空气与结构相互作用和热黏性对混合共振基元及空间卷曲基元声透射和相位调制的影响.结果表明,耗散对相位的影响较小,但对透射强度的影响较大.对于具有狭长声通道的系统,热黏性效应非常明显.空气与结构相互作用可能导致结构共振和反共振 (类法诺共振),在设计超表面时,应通过选择适当的工作频率来避免这种情况,尤其是对于声阻抗较低的材料.值得注意的是,损耗并不总是有负面影响.相反,损耗引入和调控可为被动波前/幅值调制提供一个新的自由度(Li et al.2017,Fan et al.2020c,Gerard &Jing 2020).

3.2 水声功能基元

众所周知,水和固体之间的声学失配小于空气和固体之间的声学失配,因此,固体的变形以及水和固体之间的动力相互作用不能忽视.这使得超表面的独立设计变得困难,因为相邻基元之间的相互作用可能非常显著(Li P et al.2020,Zhou et al.2021a).一些学者试图将空气声的基元设计扩展到水声.例如,Yang X Y 等(2019)基于广义斯涅尔定律,利用空间卷曲基元构建了超表面 (具有波长厚度),用于水下超声 (2MHz) 的聚焦.数值分析表明,声阻抗大的固体材料可以产生良好的聚焦性能.Wu 等(2016)使用类直井基元设计了反射超表面,实现了水下超声波的轴对称聚焦.Cheng 等(2018)设计了具有复合介质 (甘油/制冷剂c318) 的层状基元,构建用于水下波束定向的超表面;同时设计了甘油制成的迷宫结构来减小超表面的厚度.然而,这一方法实际上不易实现.Jin 等(2019)报道了一种新型的相位梯度超表面,它由高折射率梯度多孔硅橡胶软材料制成,数值模拟和实验结果均展示了其在水中实现宽频超声三维波前调控的能力.

Zhou 等(2021a)提出了一种类亥姆霍兹共振的基元,用于设计实现水声转向的反射超表面,如图12(a)所示.该超表面厚度可比波长小几十倍.他们研究了基元间的动力相互作用对波前调制的影响,研究表明,当不同的基元组装在一起构建超表面时,每个独立基元调制的声场 (图12(b))会发生畸变 (图12(c)).导致该现象的原因如下: 单个基元的计算中应用了周期边界条件 (见图6),然而,当不同的基元组装在一起时,周期性被破坏,基元的振动模式被改变 (对比图12(b)和图12(c)中的插图),最终,由于强烈的流固相互作用,导致反射声场失真.但对于空气声,空气和固体之间的相互作用非常微弱,其影响可以忽略 (参见文献(Zhou et al.2021a)中的附录D).Zhou 等(2021a)的研究表明,基于广义斯涅尔定律的局部设计不能很好地实现波的调控,尤其是对于图12(d)所示的大反射角情况.基于格栅衍射理论并通过优化方法实施的非局部设计,可以实现高效的波前调制,如图12(e)所示.最近,Zhou 等(2022)指出,抑制基元之间的动力相互作用对于改善局部设计至关重要.他们基于表面阻抗定理实现了反射超表面的局部设计.其中采用了拓扑优化的方法,通过削弱相邻基元之间的振动耦合来优化基元的微观结构,实现了包括大角度异常反射、行波转倏逝波以及超分辨率近场聚焦等精确的波前调控.

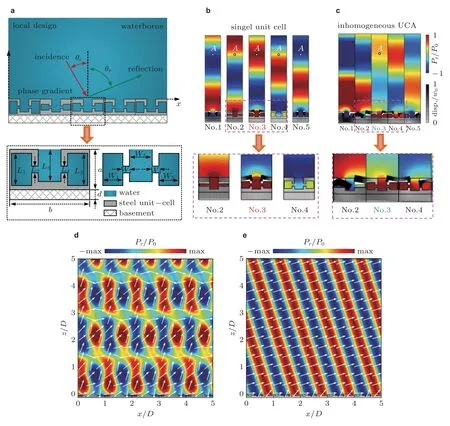
图12 类亥姆霍兹共振基元构建的可实现水声转向的反射超表面(Zhou et al.2021a).(a)超表面和类亥姆霍兹共振基元,(b)单个基元的相位调控,(c)组装的基元阵列的相位调控(水域由内部声场硬边界隔离以消除声干扰),(d)基于广义斯涅尔定律的超表面所调控的反射场(局部设计),(e)基于格栅衍射理论的超表面所调控的反射场 (非局部设计)

人们还提出了一些其他类型的共振基元来构建水声超表面.例如,图13(a)显示了Chen Z等(2020)提出的共振基元,该基元由一个铝制空气腔和一个连接在顶部的铅块组成.它实际上像一个板状 (或膜状) 基元,板的厚度与相移有关.基于广义斯涅尔定律,作者利用由该基元构建的超表面在数值上实现了波束定向、聚焦和地毯隐身等功能(Chen Z et al.2020).随后,上述基元进一步被改进为一种极薄的基元,该基元由一个覆盖着薄钢板的空腔组成,钢板用橡胶垫片固定在钢支架上(Chen Z et al.2021).他们以此基元构造了极薄的超表面 (λ/61.7),展示了水声的锐聚焦、自弯曲和地毯隐身功能.Zou 等(2020)设计了一个多重共振基元,它由粘结在两块钢板之间的矩形泡沫基体和一个含多个质量块的夹杂物组成,其中夹杂物由四根矩形钢棒围绕的硬橡胶圆柱体嵌入软橡胶圆柱体中组成,如图13(b)所示,可诱发单极、偶极和四极共振.改变软橡胶圆柱体的半径可以产生在2π 范围内变化的相移.作者基于广义斯涅尔定律,利用此基元构建超表面实现了异常反射、聚焦和地毯隐身等功能.Li P 等(2020)提出了一种各向异性共振基元,如图13(c)所示,该基元包括一个方形环氧框架和一个在中心含有椭圆形共振器的圆形充水腔,椭圆形共振器具有三种组分材料 (环氧壳/橡胶夹层/钢芯),可以提供偶极共振.旋转椭圆共振器可以调节反射相移.组成超表面时在相邻基元之间引入空气缝隙,以减少基元之间的相互作用,从而使基于广义斯涅尔定律的局部设计成为可能.Xu Z H 等(2022)提出了一种类似的,但不包括充水腔的不可调各向异性共振基元.如Liu M Y 等(2019)所述,反射波的相移也可以通过改变上述不可调基元中的钢芯半径来调整.

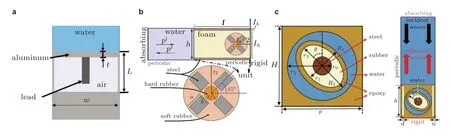
图13 水声功能基元.(a)板状基元(Chen Z et al.2020),(b)多质量共振基元(Zou H Z et al.2020),(c)多层共振基元(Li P et al.2020)

另一类专门用于水声调控的超表面由五模材料构成,五模材料由Milton 和Cherkaev(1995)提出.由传统固体 (通常为金属) 制成的五模材料很难压缩,但很容易流动,其行为类似于液体(因此称为金属水).另一方面,它们是稳定的,可通过制备获得空间不均匀性和/或各向异性,这非常有利于调控水声(Chen Y et al.2016).通常,五模材料单元由蜂窝状格栅和附加重量 (材料与格栅相同或不同) 组成.单元的等效密度和各向异性程度可分别通过附加重量和几何构型进行调整.如图14(a)(Tian et al.2015,Chu et al.2020)和图14(b)(Cai et al.2017,Chen &Hu 2019,Liu Y et al.2019)所示,附加重量可以设置在六边形顶点也可以设置在蜂窝壁中点.上述结构可用于设计超表面实现诸如异常折射/反射、聚焦和波前转换等各种衍射调控功能.如最近Zhang X D 等(2020)制作了一个五模材料超表面 (如图14(c)所示),当声波垂直入射时,实现了对反射波的调控.Sun 等(2021)提出了阻抗匹配五模材料超表面的理论设计,该超表面由8个类似矩形的结构 (如图14(d)中的右图所示) 围绕z轴旋转π/4 而构成.超表面可以将平面声波扭转成具有螺旋波前的涡旋波,如图14(d)所示.他们还讨论了其在水声复用通信中的可能应用.

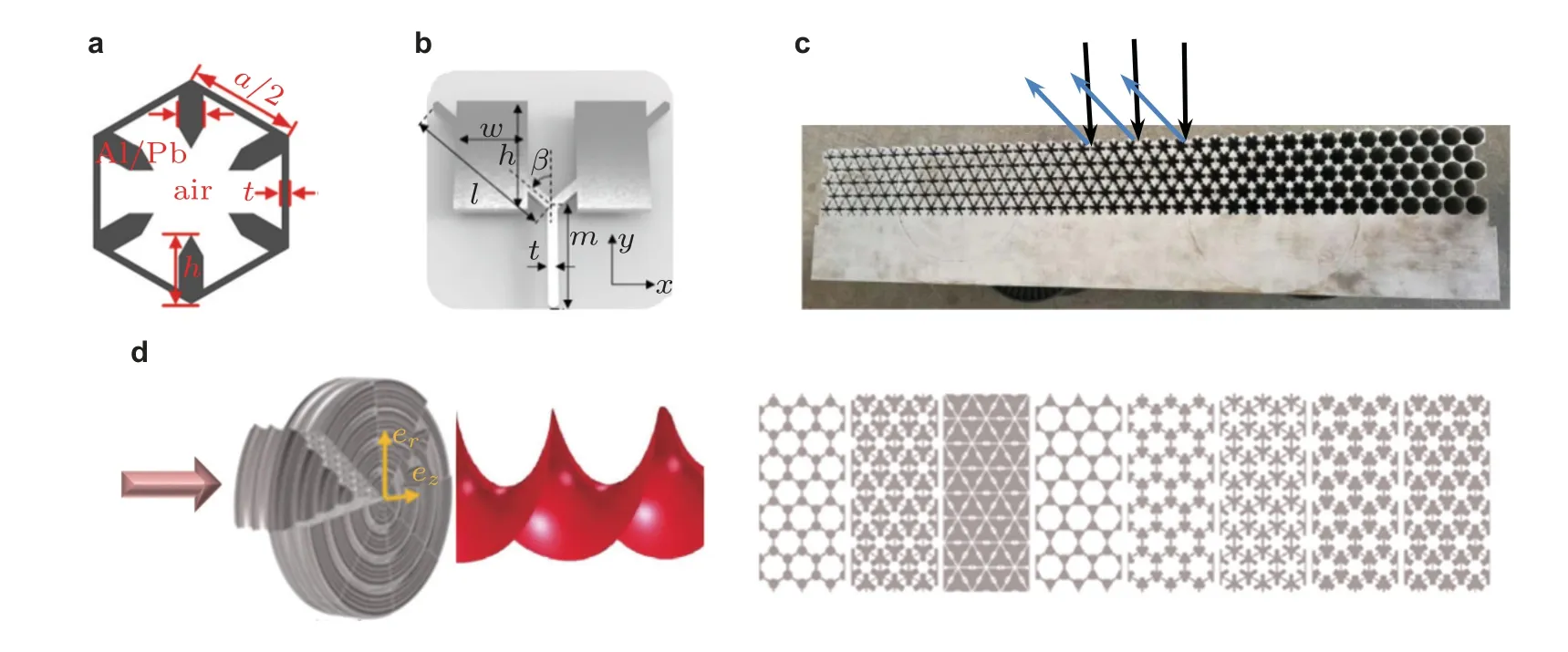
图14 五膜材料水声超表面.(a)附加重量处于六边形顶点的五模材料单元(Tian et al.2015),(b)附加重量处于蜂窝壁中点的五模材料单元(Chen &Hu2019),(c)调控反射波的五模材料超表面(Zhang X D et al.2020),(d)产生涡旋声波的五模材料超表面(Sun et al.2021)

总体来说,与空气声的情况不同,水声的功能基元仍然很有限.高效超薄超表面的局部或非局部设计都具有挑战性.另外,为了实现水声的自由调制,五膜材料在构造超表面时需要具有大范围的等效质量密度和各向异性模量.

3.3 弹性波功能基元

与空气声和水声不同,在固体中传播的弹性波是矢量波,包括耦合的且速度不同的纵波 (L)和横波 (T) 模式.而且,除了块体材料中的体波外,还有其他模式的波,例如板或壳中的导波、沿固体表面传播的表面波等.总之,弹性波比标量声波复杂得多.在弹性功能基元和超表面的设计中,有许多具有挑战性的问题.例如,超表面能否同时调制入射的L 波和T 波？如何设计一个基元来实现不同波模式之间的转换？在设计用于调节一种波模式 (如L 波) 的超表面时,将产生另一种模式的波 (T 波) (Shen X H et al.2018,Yuan et al.2020b),那么,这种波 (T 波) 的反射或折射行为如何？由于这些困难,至今对弹性超表面的研究仍然很有限.

为了调制块体材料中的弹性体波,Su 和Norris(2016)及Su 等(2018)引入了平行狭缝以形成平行板阵列,如图15(a)所示.其中,板厚的变化可以调节T 波速度 (但不能调节L 波速度),从而调节入射T 波的相移 (见图15(a));而长度的改变可同时影响L 波和T 波的速度,进而可以调控L 波和T 波的相移.基于这种设计策略,可以实现SV 波的转向和聚焦(Su &Norris 2016,Liu Y L et al.2020)、P 波的不对称传输(Su &Norris 2016)以及P 波和SV 波的分离(Su et al.2018).随后,该板状基元被扩展为如图15(b)所示的复合板状基元(Cao et al.2018b,Zhang et al.2018a,Zeng L H et al.2019),相移由两个连接部分的长度比控制.上述板状基元的一个优点是可以依据板理论获得解析解.但是,构造的超表面不够薄,通常约为一个波长.另一种调节体波的简单基元是多层基元(Shen X H et al.2018,Su et al.2020),通过调节其中组分材料的体积分数可以改变波速,从而获得不同的相移.

大多数关于弹性超表面的研究工作集中于板结构中兰姆波的调控.类比于体波的板状或复合板状基元,人们提出了条状(Qiu et al.2019,Qiu &Li 2020)或复合条状基元(Zhang J et al.2019).另一种复合条状基元由Tian 和Yu(2019)提出,该基元通过在基板条上粘贴覆板条形成.Jiang Y Q 等(2022)提出了一种基元,由平行于超表面的狭缝 (或缺口) 阵列组成,相移可以通过独立调节多个参数来调控.另外,学者们还设计了弧形条状基元,通过改变弧长来调节透射SH0波的相位(Cao X et al.2021).遗憾的是,利用这些条状 (或狭缝) 基元设计的超表面,其厚度约为一个波长.为了实现亚波长超表面设计,Liu 等(2017)提出了一个具有多个弯折的锯齿形基元,如图15(c)所示.通过改变弯折高度 (h),可以产生在整个2π 范围内变化的相移和近乎单位1 的传输.他们基于此设计了圆形超表面 (如图15(c)所示),作为弯曲兰姆波源幻象装置.此后,类似的基元被用于实现对板导波的各种操控(Li B et al.2020,Zhang et al.2020b,Jiang M et al.2022).实际上,锯齿形基元调节相移的能力归功于其多模态共振减慢了波的传播,因此它实际上是一种共振基元.

最近,人们提出了各种各样的局部共振基元.图15(d)和图15(e)所示的为通过切割母板得到的局部共振基元(Lee et al.2018,2020).图15(d)中带有狭缝的上部和下部区域被称为刚度调节子结构,用于改变有效刚度;而中间由局域偶极谐振器组成的质量调谐子结构用来改变单元的等效质量.Lee 等(2018)通过数值和实验证明了利用该单元构造的超表面可实现兰姆波中S0 模态 (接近于L 模态) 的波束转向.图15(e)所示的基元包含两种谐振器,即水平谐振器和竖直谐振器,它们可以分别将等效质量和刚度从负值调整为正值(Lee et al.2020).值得指出的是,竖直谐振器中包含了惯性放大机构(Yilmaz et al.2007,Van Damme et al.2021).调整两个谐振器的尺寸 (图中h1和h2) 可以产生所需的相移.上述共振基元可以用来构造非常薄的超表面,用于实现模式转换、定向折射和聚焦(Lee et al.2020,Lee &Oh 2020).其他通过切割母板来实现波模式转换和波束分裂功能的基元,请参考文献(Yang X W et al.2019,Zheng et al.2020).局部共振基元也可以通过在母板中嵌入带有弱连接的质量块来构造(Zhu &Semperlotti 2016,Zhu H F et al.2018),其中质量块和母板可以由相同(Zhu &Semperlotti 2016)或不同的材料构成 (见图15(f)(Zhu H F et al.2018)).Lin Z B 等(2021)将类立方振荡器组装到连杆中,形成了共振基元.立柱状共振结构已广泛用于声子晶体和超材料的设计中(Jin et al.2017),也可用于构造相位梯度超表面,改变立柱高度可以调节相移.Cao L Y 等(2018a,2018c,2020b,2021)为实现弯曲波操控设计了各种立柱弹性超表面,其中功能基元由周期 (图15(g) (Cao L Y et al.2018a,2018c,2021))或随机 (图15(h)(Cao L Y et al.2020b)) 分布的立柱阵列组成.上述设计中基元一般通过狭窄缝隙隔离开(Cao L Y et al.2018a,2018c,2020b),以抑制基元之间的干扰.而在设计高效超表面时,则应合理考虑基元之间的相互干涉(Cao L Y et al.2021).Jin 等(2021)和Wang 等(2021a)证明,即使只有一排柱子 (如图15(i)所示),超表面也可以实现弯曲波聚焦和亚波长成像 (Jin et al.2021).

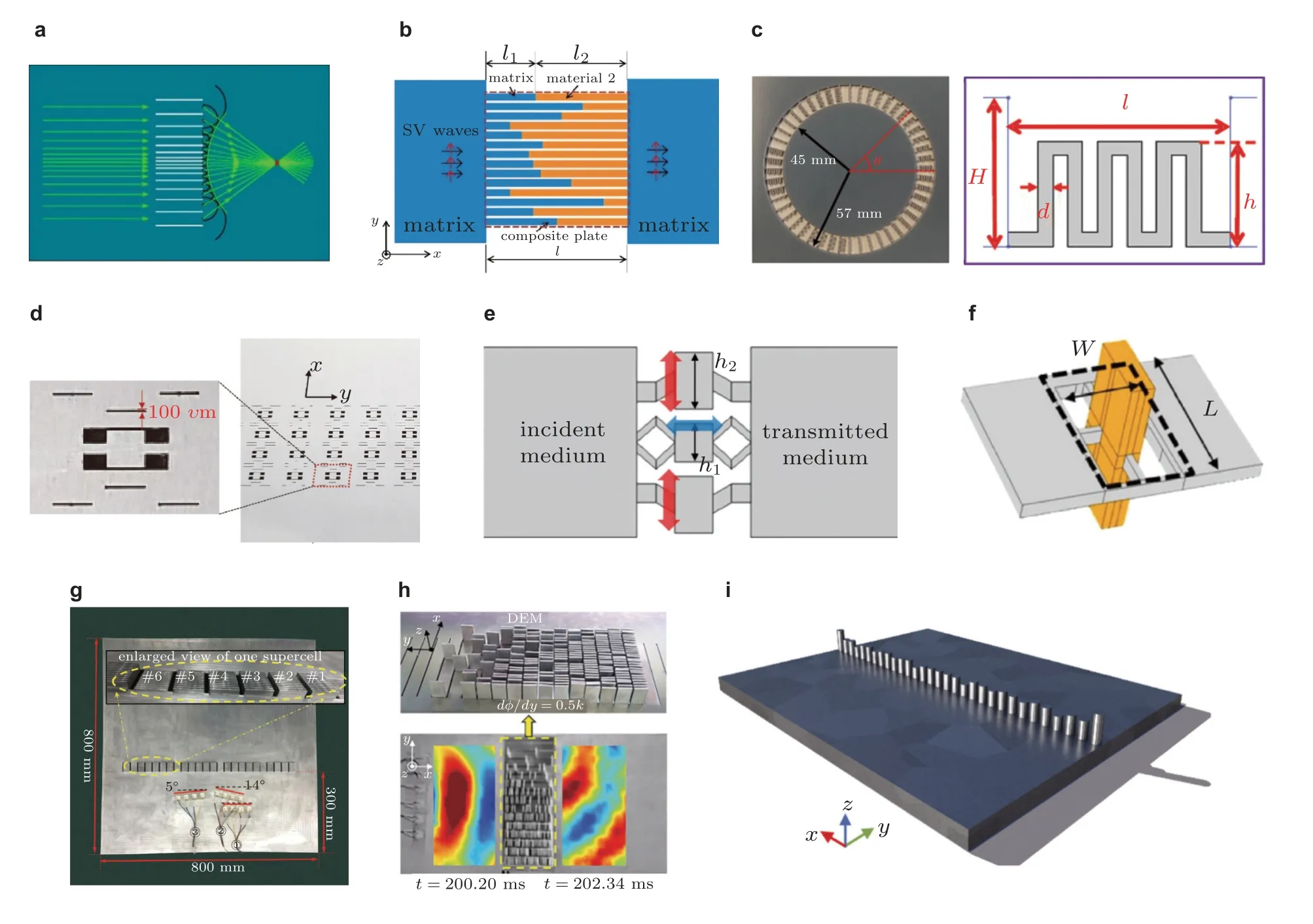
图15 弹性波透射型基元.(a)板状基元(Su et al.2016),(b)复合板状基元(Zeng L H et al.2019),(c)锯齿形基元(Liu et al.2017),(d)具有刚度和质量调节子结构的组合共振基元(Lee et al.2018),(e)具有水平和竖直谐振器的共振基元 (Lee et al.2020),(f)嵌入共振体的共振基元(Zhu H F et al.2018),(g)周期立柱阵列基元(Cao et al.2018c),(h)随机分布立柱阵列基元 (Cao et al.2020b),(i)仅由一排立柱构成的超表面(Wang et al.2021a)

Xu 等(2019a)提出了一种具有单个凹槽的特殊基元来构建超表面,实现了异常折射、波束弯曲和源幻像等功能.当兰姆波与凹槽相互作用时,将发生模式转换 (例如,从S0 模式转换到A0 模式).因此,可以通过调节凹槽位置来实现调制透射波所需的相移.基于类似的相位调制机理,他们还设计了一种具有缺口对 (正槽和倒槽) 的基元,以构建调控兰姆波异常折射、波束弯曲和波聚焦的超表面(Xu et al.2019b).最近,为了获得更好的波前调控性能,他们基于遗传算法对单槽超表面进行了拓扑优化(Lin et al.2022),确定了正槽和倒槽的精确位置.

操控反射波的超表面受到的关注较少.Kim 等(2018,2020,2021)使用了条状基元来设计超表面 (见图16(a)),实现了反射波转向/分裂、模式转换等功能,其中条带长度的变化产生了2π范围的相移.Cao 等(2020a)提出了一种含有黏弹性层的复合条状单元,同时实现了吸收和波前调控.Ruan 等(2020)通过在板边缘的两侧粘贴不同厚度的条带,设计了如图16(b)所示的反射超表面,并数值演示了弯曲波的回射功能.条状基元的一个缺点是,相应的超表面的厚度通常大于一个波长.有待提出新型的高效反射基元设计.

图16 弹性波反射型基元.(a)条状基元及超表面(Kim et al.2020),(b)板边缘粘贴不同厚度条带构成的条状基元(Ruan et al.2020)

3.4 基元的改进设计

上面提到的功能基元都是一些基本的设计,可产生在2π 范围内变化的相移并用于构建相位梯度超表面来实现声波或弹性波的波前调控.但是,在某些情况下,例如,当基于表面阻抗定理设计非局部 (反射) 或双各向异性 (透射) 超表面时,或当超表面具有独立调控的相位和幅值时,可能需要对基元设计进行改进,以实现波的高效精准调控.本小节将介绍一些改进的基元设计,包括非局部基元、双各向异性基元、拓扑优化基元和组合基元等.

3.4.1 非局部基元

如2.3.1 节所述,基于表面阻抗定理构建高效反射非局部超表面的有效方法之一是设计非局部基元,这些基元之间有通道连接,以提供横向能量交换并保持能量守恒.Quan 和Alú(2019b)设置相邻基元之间的连接通道,针对空气声提出了一种非局部基元,如图17(a)中的左图所示.他们利用该非局部单元,实现了能流系数为单位1 的完美反射.比较图17(a)中右侧框图所示的两种情况可以看到,分别由非局部和局部基元构建的超表面对波场调制的效果有显著差异.类似的设计也被用于实现超宽带吸声(Zhu et al.2021b)或产生具有双曲线波前的表面波(Quan &Alú 2019a).Zhu 等通过引入非局部设计构建了平直(Zhu H F et al.2020)和圆形(Zhu et al.2022)弹性超表面,实现了弹性波的宽频全内反射.他们设计的结构如图17(b)所示,其中非局部效应通过设置连接多个单元 (黄色部分) 的柔性梁状构件 (深灰色部分) 而实现.无修饰(Fan &Mei 2020)或有修饰(Schwan et al.2018) (如图17(c)所示) 的周期排列散射体也可用于构成声学超表面,其中的非局部效应由散射体之间的相互作用产生.考虑到应变和速度之间的交叉耦合(即Willis 耦合),Quan 等(2018)和Esfahlani 等(2021)分别使用有修饰的圆柱体 (如图17(d)所示) 和球形亥姆霍兹共振腔 (如图17(e)所示) 构建了声学超表面.其中,Quan 等(2018)利用优化的Willis 散射体构建的超表面将反射波调控到极大反射角方向并具有单位能流反射系数,而Esfahlani 等(2021)则实现了全反射和不对称吸收.Willis 散射体还可用于构建宽频声屏障(Popa et al.2018).值得注意的是,Willis 耦合类似于电磁学中的双各向异性现象.

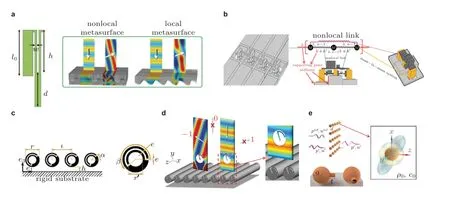
图17 非局部基元.(a)空气通道连接的基元及由局部和非局部超表面调控的反射场对比(Quan &Alú 2019b),(b)具有非局部基元的弹性超表面(Zhu H F et al.2020),(c)有修饰的周期排列散射体构建的非局部超表面(Schwan et al.2018),(d)有修饰的圆柱体构建的非局部超表面(Quan et al.2018),(e)球形亥姆霍兹共振腔构建的非局部超表面(Esfahlani et al.2021)

3.4.2 双向异性基元

如第2.3.2 节所述,Díaz-Rubio 和Tretyakov(2017)的研究表明,实现透射波场高效调制的超表面是局部、被动、无损的,但应是双各向异性的.然而,双各向异性基元的设计并非易事.Díaz-Rubio 和Tretyakov (2017)用到的三层膜基元是一个简单的双各向异性基元,他们利用此基元数值实现了理想折射 (perfect refraction),但这在实际中并不容易实施.Li J F 等(2018)提出了一种双各向异性基元,如图18(a)所示,该基元包含一条直通道和四个亥姆霍兹共振腔.它具有反射相位不对称的特征,即在相反方向上反射波的相位不同 (参见图18(a)中的右图),这是双各向异性基元的显著特征.Li J F 等(2018)从数值和实验两方面证明该基元可成功实现无散射异常折射.随后,Li J F 等(2019)利用此基元构造了一个圆形超表面,以产生角动量为12 的波束;Li J F 等(2020)通过引入自诱导的表面波,同时实现了对反射场和透射场的任意控制.非对称三明治空间卷曲基元也表现出双各向异性,Tong 等(2021)用此基元构造了超表面.一般来说,双各向异性行为可通过在基元中引入不对称性来实现.Koo 等(2016)通过波参数解耦,发展了另一种由薄膜和固体壁组成的双各向异性基元 (见图18(b)中的左图),他们利用此基元实现了透射波和反射波的独立调控,如图18(b)中的中间和右侧图所示.

图18 双各向异性基元.(a)直通道上连接不同亥姆霍兹共振腔的基元及其非对称性(Li J F et al.2018),(b)具有解耦波参数的基元及透射和反射波的独立调控(Koo et al.2016)

3.4.3 拓扑优化基元

上述基本的基元设计,通常通过调整一个几何参数来实现2π 范围内的相移.这虽然简单,但可能较难获得高效或宽频的波前调控或得到超薄的超表面.参数优化方法可以给出具有相同拓扑结构但形状和尺寸各异的基元,已被用于提高超表面效率,尤其是用于非局部超表面设计 (参见文献(Zhu H F et al.2020;Zhou et al.2021a,2021b;Zhu et al.2021b)),因为此时相移调制需要通过调节一组几何参数来实现.相对而言,拓扑优化方法可以提供各种出人意料的能够满足特定优化目标的基元构型.基元拓扑结构的变化也能产生相位梯度.近年来,声学/弹性超表面的拓扑优化越来越受到人们的关注.Noguchi 和Yamada(2021)以空气声的负折射为目标,采用基于水平集的拓扑优化方法设计了一个双层超表面,他们基于均匀化理论对具有所需相移的基元进行了优化.Dong 等(2022a)利用基于遗传算法的拓扑优化方法设计了声学超表面,并通过数值和实验实现了超宽带波束定向、聚焦和声悬浮.图19(a)显示了其中一些优化的基元,它们是含有多个散射体、弯曲声通道和局部空腔的新型不对称几何结构.文中指出,定制的超宽带色散特性归因于内共振、双各向异性和多散射的共同作用 (Dong et al.2022a).基于表面阻抗定理,Zhou 等(2022)利用拓扑优化方法设计了水声反射超表面,其基元由一个覆盖有环氧树脂板并填充了有损耗橡胶的U 形钢槽组成.文章对嵌入橡胶中的钢夹杂物的形状和分布进行了优化,在考虑固体基元之间弱振动耦合的情况下得到了所需的相位和幅值.Ahn 等(2019)发展了一种基于密度的拓扑优化方法来设计弹性超表面,以实现L 波的异常反射,包括大反射角和极限反射角的情况,并在优化的波导中实现了波的聚焦和俘获.Rong 和Ye(2020)采用基于遗传算法的拓扑优化方法,设计了同时调控L 波和T 波的弹性超表面.图19(b)显示了针对入射L 波和T 波可产生不同相移的优化基元.Rong 等(2020)利用拓扑优化方法设计了一种频率编码的多功能透射弹性超表面,并通过数值和实验证明: 可以通过调节工作频率来控制波的传播方向或聚焦点.除了相位梯度超表面外,拓扑优化方法还被用来设计可将空气声纵波转为弹性横波的超表面(Noguchi et al.2015),以及不考虑相位梯度的通风隔音超表面(Miyata et al.2018).总的来说,优化方法为设计具有所需相移和幅值,甚至可实现弹性波模态转换的基元提供了强有利的工具.

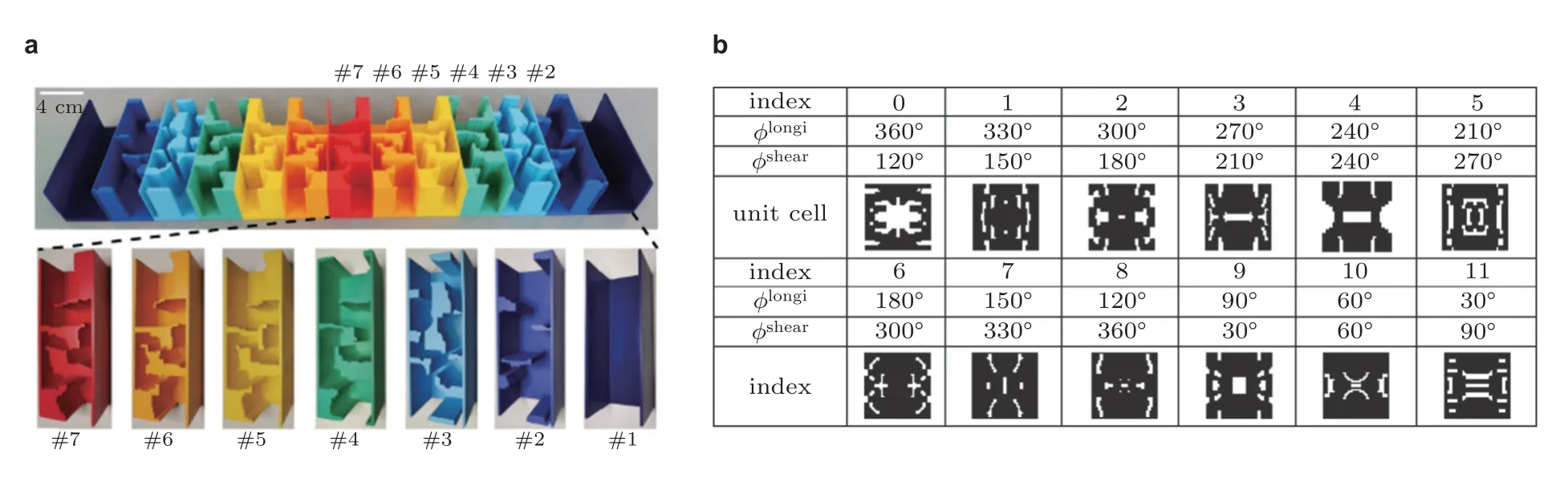
图19 拓扑优化基元.(a)具有不对称几何结构的空气声拓扑优化基元(Dong et al.2022a),(b)同时调控弹性L 波和T 波的拓扑优化基元(Rong &Ye2020)

3.4.4 组合基元

为了实现高质量的全波场调控以实现复杂的功能,上述功能基元也可以用作子单元来构建组合基元.例如,相位和幅值的解耦调制为声全息超表面提供了灵活的设计,而相位和幅值的解耦调制通常需要对组合基元进行精细设计(Tian et al.2017,Zhang H K et al.2020,Zhu et al.2021a).Tian 等(2017)提出了一种组合基元,如图20(a)所示,该基元由三层空间卷曲结构和一条直通道组成.其中空间卷曲结构用于提供完整2π 范围内变化的相移 (通过改变li) 并具有几乎为单位1 的透射率;而直通道则用于整个范围的幅值调控 (通过改变Wp),其相移为常数,如图20(b)所示.利用此组合基元设计超表面可实现多方向透射、多点聚焦和声全息成像(Tian et al.2017).使用类似的组合基元,Zhang H K 等(2020)构建了超表面,在实验上实现了声涡旋结.图20(c)(Zhu et al.2021a)所示的双通道组合基元可用于设计多路复用的高质量声学超全息,其中组合基元的每个通道对应一个共振频率.基元中的频率调制器 (蓝色部分)、幅值调制器 (黑色部分) 和相位调制器 (红色部分) 分别主要调节透射波的频率、幅值和相位(Zhu et al.2021a).Zuo 等 (2018a)还使用了由一个空间卷曲结构和一个直通道组成的组合基元来实现基于超表面的模拟计算.组合元件的缺点之一是,构造的超表面其厚度可能大于一个波长(Zhang H K et al.2020,Zhu et al.2021a).

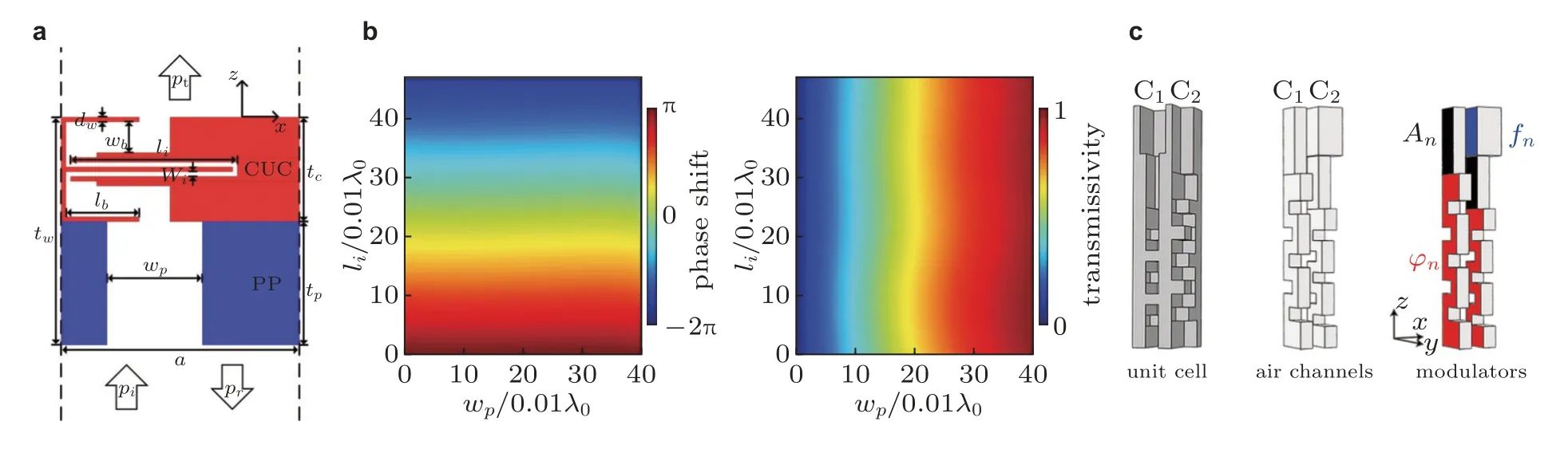
图20 组合基元.(a)由空间卷曲结构和直通道组合而成的基元(Tian et al.2017),(b)相位和幅值的解耦调制(Tian et al.2017),(c)双通道组合基元(Zhu et al.2021a)

4 波场操控及应用

依据第2 节介绍的设计原则,通过恰当选择上面提到的功能基元,可以设计超表面来灵活地调控波前的方向或形状.控制波前方向可以实现异常折射/反射、波束分裂和波束聚焦 (产生无衍射Bessel 波束) 等功能;波前形状的调制可以实现点聚焦、自弯曲和涡旋波束等.一些更复杂的功能,例如非对称传输、声全息、模拟计算、粒子悬浮/输运等,则可能需要引入额外的调制参数如幅值,甚至需要通过使用两个超表面来实现.以下将简要介绍声学/弹性超表面波场操控的若干示例以及相关的潜在应用.

4.1 异常折射/反射

异常折射/反射将波前方向引导到所需方向,是超表面最基本的功能,也是实现复杂功能的前提.利用超表面可以实现空气声(Mei &Wu 2014,Tang et al.2014,Ding et al.2015,Zhu Y F et al.2016,Li J F et al.2018,Quan &Alú 2019b)、水声(Tian et al.2015,Cheng et al.2018,Zhang X D et al.2020,Zou H Z et al.2020)和弹性波(Cao L Y et al.2018c,Lee et al.2018,Zhang et al.2018a,Cao et al.2020a)的这一基本功能.通常,基于广义斯涅尔定律设计的超表面可以很好地实现该功能(Li Y et al.2013a,Cai et al.2017,Shen X H et al.2018,Zhang X D et al.2020,Liu et al.2022).然而,基于格栅衍射理论(Xie Y B et al.2014,Wang W Q et al.2016,Kim et al.2020)和表面阻抗定理(Díaz-Rubio &Tretyakov 2017;Li J F et al.2018,2020)设计的超表面可以实现高质量和高效率的异常折射/反射,尤其是对于大折射/反射角的情况.一些有趣的功能,如回射(Liu et al.2017b,Shen C et al.2018,Ruan et al.2020)、凋落模式转换 (即行波转表面波) (Zhao et al.2013a;Zhai et al.2015;Wang et al.2016b;Lan et al.2017a,2018;Chu et al.2020;Yuan et al.2020a,2020b)和波束分裂(Li et al.2016,Cao et al.2018b,Zhang J et al.2019,Fan &Mei 2020,Li J F et al.2020,Kim et al.2021,Yan et al.2021),如图21(a)～图21(c)所示,可以视为异常折射/反射的特例.对于弹性波,如图21(d)所示的P 波和SV 波模式分离(Su et al.2018,Rong &Ye 2020)和模式转换 (如图21(e)显示的入射P 波转为SV 波(Shen X H et al.2018,Lee et al.2020),或入射的对称兰姆波模式 (S0) 转为反对称模式 (A0) (Zhu &Semperlotti 2016)) 也是令人感兴趣的课题.Esfahlani 等(2016)、Li X S 等(2019,2020)和Zhao 等(2013b)讨论了散射波在入射面外的三维波场调制,如图21(f)所示.非平面超表面也被用于实现异常反射(Li X S et al.2020)或折射(Ju et al.2019,Chen A L et al.2021),尤其是Li X S 等(2020)研究了任意曲面形状的超表面.定向或多方向折射/反射具有很多潜在的应用.例如,如图21(g)、(h)所示,定向反射可用于地毯隐身或地表幻象 (参考文献(Esfahlani et al.2016;Faure et al.2016;Wang et al.2016b,2017;Chen et al.2018;Ma F Y et al.2018,2019a,2019b;Chen Z et al.2020;Fan et al.2020b;He et al.2020;Li X S et al.2020;Zhou H T et al.2020;Zhou et al.2021b)等).相反地,在某些情况下,例如在礼堂、音乐厅或电影院里,不管入射角度如何,通常要求声音在各个方向上均匀散射,因此扩散装置会有所帮助.基于声学超表面,Zhu等(2017)提出了一种新的超薄平面三维 Schroeder 扩散器,实现了完美的漫散射 (如图21(i)所示),其厚度约为传统扩散器的十分之一.最近,Zhao 等(2020)通过使用宽度为λ/4 (文献(Zhu et al.2017)中为λ/2) 的类亥姆霍兹共振基元,设计了一种基于超表面的超薄平面型二维漫散射器,以实现高度均匀的窄带漫反射.

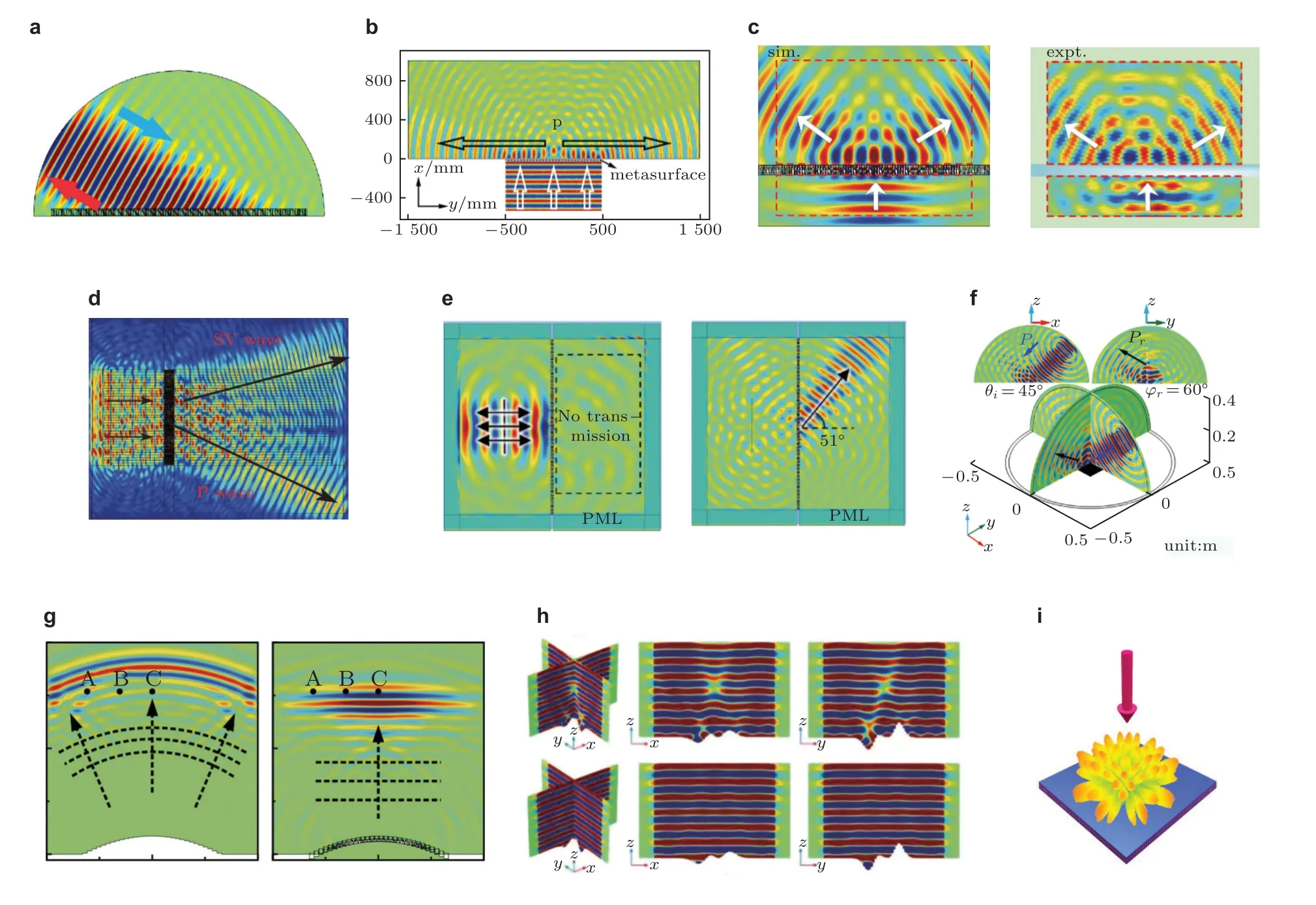
图21 异常折射/反射.(a)回射(Shen C et al.2018),(b)行波转表面波(Zhai et al.2015),(c)波束分裂(Li J F et al.2020),(d)P 波和SV 波模式分离(Rong &Ye 2020),(e)P 波转SV 波(Lee et al.2020),(f)入射面以外的反射波调制(Li X S et al.2019),(g)弧状超表面实现地毯隐身(Zhou et al.2021b),(h)从曲面到平面的地表幻象(Li X S et al.2020),(i)超薄Schroeder 扩散器实现扩散散射(Zhu et al.2017)

4.2 波聚焦

聚焦是超表面的另一个重要功能,可以使波能量集中在某个点 (点聚焦) 或某个区域 (波束聚焦,例如无衍射Bessel 波束).其中关于空气声(Li et al.2014,Zhu et al.2015a,Jahdali &Wu 2016,Tang W P et al.2019,Zhu &Assouar 2019a,Chen A L et al.2020)、水声(Yang X Y et al.2019,Lawrence et al.2020,Li P et al.2020)和弹性波(Lee et al.2018,Qiu &Li 2020,Wang et al.2021a)的二维点聚焦功能 (包括斜聚焦) 已经得到了广泛的研究.另外,空气声(Zhai et al.2015,2016;Lan et al.2017b;Chen A L et al.2021)和水声(Tian et al.2015,Liu Y et al.2019)的Bessel 波束也已有报道,如图22(a)所示.Liang 等(2022)设计了一种圆形锯齿结构,该结构与扇形平面换能器的环形阵列相连,在水下产生了Bessel 涡旋声束.三维轴对称(Molerón et al.2014,Li et al.2015b,Wu et al.2016,Chen J et al.2019,Jin et al.2019)或非轴对称(Li X S et al.2019,2020;Jiang X et al.2022) (见图22(b)) 点聚焦也可通过平面或曲面(Li X S et al.2020)超表面实现.Wang Y H 等(2019)数值实现了包括Gaussian 波束和Bessel 波束在内的三维轴对称波束聚焦.众所周知,具有点聚焦功能的超表面可用于设计能够成像的超薄平面透镜.此外,聚焦还可以通过限制或局域各种环境中的声音/噪声 (如图22(c)所示) 并将其转换为电能,实现能量收集(Qi &Assouar 2017,Qi et al.2017).另一方面,圆柱(Tian et al.2015,Lan et al.2017b,Tang &Ren 2017,Ghaffarivardavagh et al.2018,Chen &Hu 2019,Liu Y et al.2019)或球面(Liang et al.2020)波前转平面波前也可通过点聚焦的反向过程来实现.

4.3 自弯曲波束

自弯曲波束,也称为自加速波束,是一种弯曲的无衍射波束,并且具有自愈性 (即波束可以绕过传播路径中的障碍物,并在通过障碍物后保持其原始轨迹).Sivilglou 和Christodoulides(2007)首次在光学领域实现了类Airy 自弯曲光束.2014年,Zhang 等(2014)利用平面扬声器阵列获得了声学自弯曲波束和三维瓶状波束 (由相交的自弯曲波束生成).2015年,Lin 等(2015)和Bar-Ziv 等(2015)分别使用带有凹槽和相位掩模的活塞式声换能器实现了水下类Airy 波束.类Airy 波束或自弯曲波束由于其无衍射、自加速和自愈合特性,在粒子捕获和操纵(Courtney et al.2014,Zhao et al.2015,Mitri 2016,Zheng et al.2011)、图像信号传输(Liang et al.2015)、能量或信息传输(Zhao et al.2014)、医疗超声成像和超声医疗方面具有潜在的应用.最近,声学(Li et al.2015a,Chen 2018,Ju et al.2019)和弹性(Chen et al.2018,Xu et al.2019a,Yuan et al.2020a,Lin Z B et al.2021)超表面也用于生成自弯曲波束.Zhu X F 等(2016)展示了自弯曲声束的自愈合特性 (如图22(d)所示);Gao 等(2016)、Chen 等(2018c)和Tang 等(2021b)讨论了自弯曲声束的高效聚焦.Jiang 等(2020a)利用二元沟槽超表面 (也称为编码超表面,见第6 节) 生成了两个圆形Airy 波束,实现了反射超声波的锐利自聚焦.Xia 等(2020)利用有损梯度声学超表面在宽频范围内获得了高质量的Airy 波束.受光学瓶状波束的启发,Memoli 等(2016)利用超表面实验生成了瓶状声束,实现了单侧声悬浮;Chen 等(2018d)利用三层空间卷曲功能基元构成的超表面实现了具有任意轨迹的瓶状波束,如图22(e)所示;Li 和Assouar (2015)利用由图10(a)所示的混合共振基元构成的声学超屏障,实现了折射声波的三维自弯曲波束或瓶状波束.另外,利用文献(Li X S et al.2021)中的轴对称曲面反射超表面生成的三维瓶状波束可形成能量空洞,如图22(f)所示.

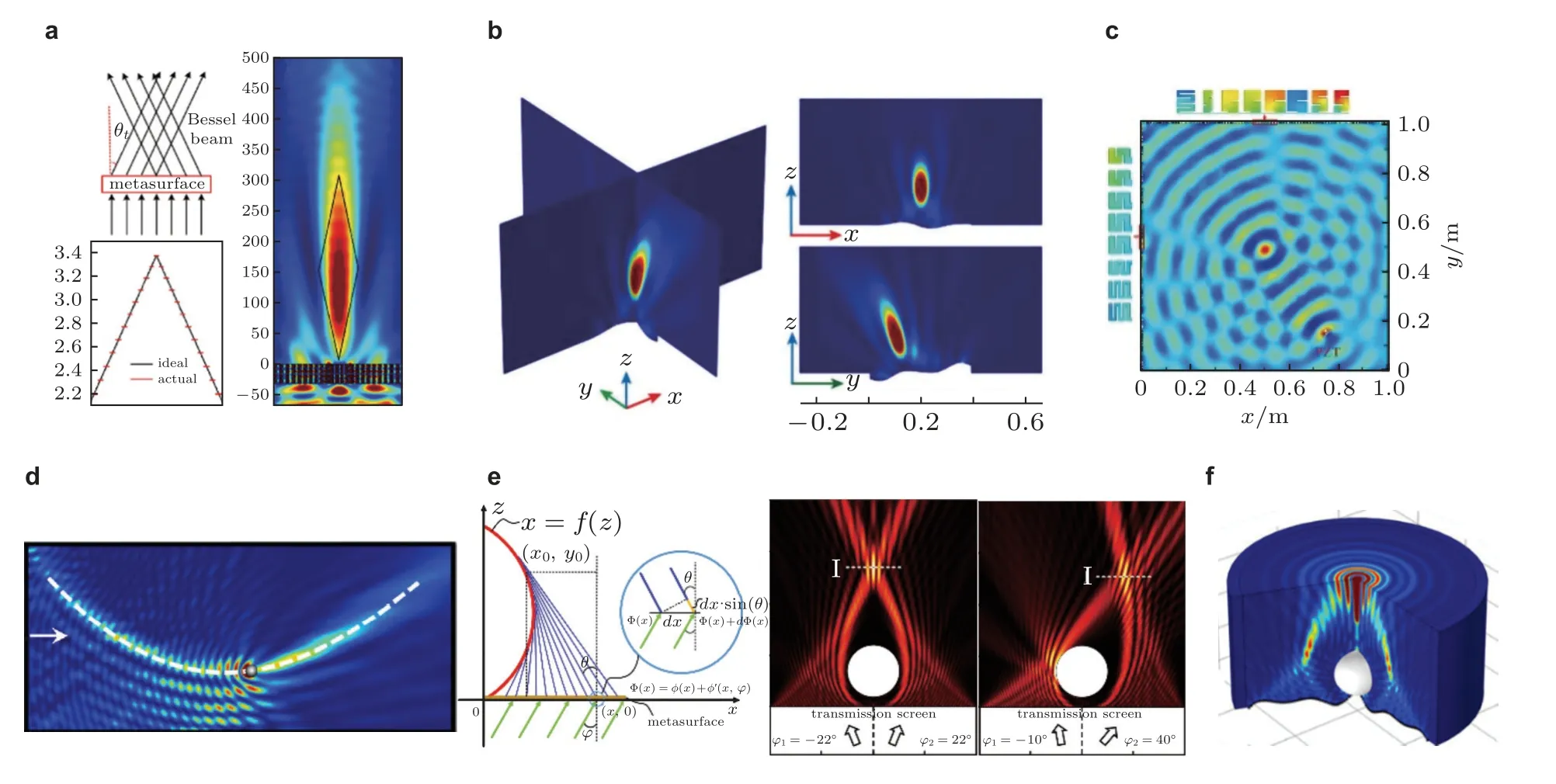
图22 波束聚焦和自弯曲.(a)Bessel 波束(Lan et al.2017b),(b)三维非轴对称点聚焦(Li X S et al.2020),(c)利用超表面实现能量收集(Qi &Assouar 2017),(d)自弯曲波束的自愈合特性(Zhu X F et al.2016),(e)具有任意轨迹的二维瓶状波束(Chen et al.2018d),(f)三维瓶状波束形成的能量空洞(Li X S et al.2021)

4.4 涡旋波束

当平面波以能够携带轨道角动量 (orbital angular momentum,OAM) 的涡旋形式传播时,波前将扭曲为螺旋形状.涡旋波在轴向中心处具有零压力幅值,并具有围绕中心轴线的螺旋状相位错exp(jmθ),其中m是拓扑阶数,θ是方位角.声涡旋波束在粒子操控(Wang T et al.2016)、声镊(Ozcelik et al.2018,Baudoin et al.2019,Gong &Baudoin 2019,Marzo &Drinkwater 2019)、声扳手或螺丝刀(Anhӓuser et al.2012,Wunenburger et al.2015)、高速声通信(Shi et al.2017)等方面有潜在的应用.最近,超表面也被用于产生声涡旋波.2016年,Ye 等(2016)通过在薄板上开阶梯截面孔形成沿圆周排布的4 个谐振器来设计超表面,实现了涡旋波,并通过实验展示了对物体的旋转操作.Jiang 等(2016a)利用图10(c)所示的具有混合共振基元的超表面,通过实验实现了从平面波到涡旋波 (m=1) 的转换.Guo Z Y 等(2019)采用了类似的结构来产生高阶涡旋.Jia Y R 等(2018)和Luo 等(2021)使用由三明治迷宫基元构成的环形声学超表面生成了分数阶声涡旋.Esfahlani 等(2017)构建了如图23(a)所示的由扭曲螺旋面组成的超表面,用以产生涡旋波.如图23(b)所示,Hou 等(2021)通过在中心含孔板的两个表面上刻槽设计了一个非局部超表面,获得了不同阶数的涡旋波.Jiang 等(2020c)利用能产生反射波相移的不同深度凹槽构建了超表面,并实现了无衍射非对称声涡旋波 (如图23(c)所示).他们的研究表明,OAM 可以被调制为任意值.Jiang 等(2016c)、Jin 等(2019)和Sun 等(2021)分别利用带盘绕缝隙的超表面、由多孔软橡胶和由五模超材料构成的超表面,生成了水下涡旋波.此外,声波(Fan X D et al.2019;Li J F et al.2019;Liu Y C et al.2020;Liu J J et al.2020,2021)和弹性波(Liu et al.2017,Xu et al.2019a,Qiu &Li 2020)的平面旋涡可由闭合的超表面产生.Zhang H K 等(2020)通过解耦相位和幅值调控,实验生成了声学Hopf 链和三叶涡结.

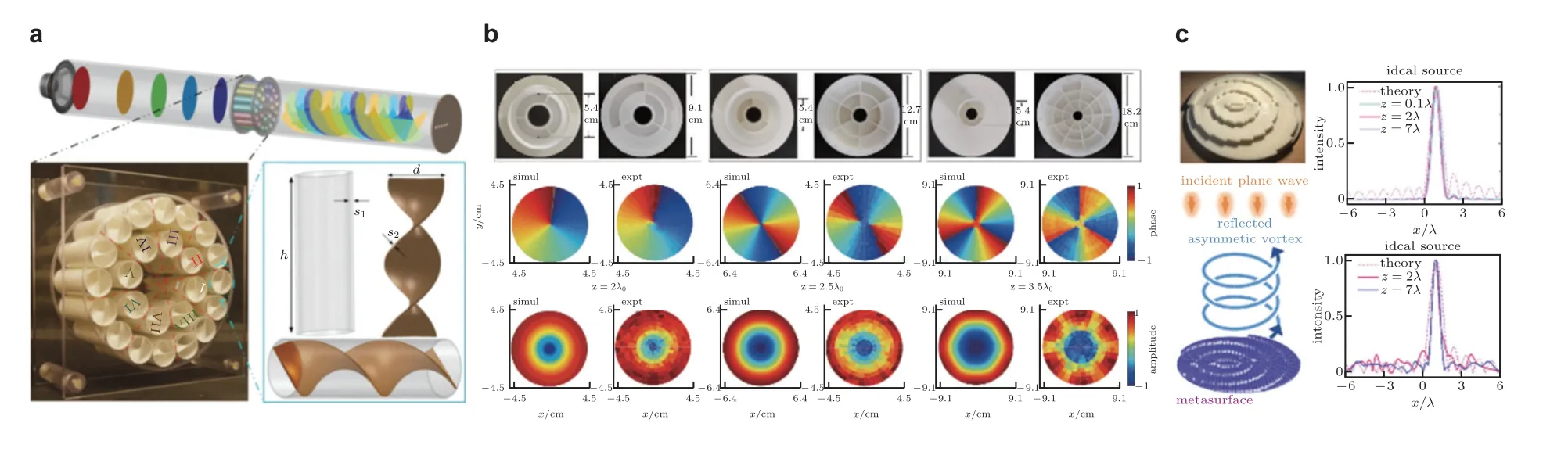
图23 涡旋波.(a)由扭曲螺旋面组成的超表面产生m=1 的涡旋波(Esfahlani et al.2017),(b)由非局部超表面产生的不同拓扑阶数的涡旋波(Hou et al.2021),(c)具有非对称零压力中心的涡旋波(Jiang et al.2020c)

除了涡旋波的生成,涡旋波的操控也是一个有吸引力和有意义的课题.Liu Y C 等(2020)、Liu B Y 等(2021)和Zeng J F 等(2019)讨论了利用两个或多个超表面实现不同拓扑阶数m的涡旋波转换的问题.Fu 等(2020a)基于拓扑阶数守恒定律,对涡旋波束的衍射进行了研究,在数值和实验上实现了涡旋波束的不对称传输.Zou Z G 等(2020)通过数值和实验研究了声涡旋波在水-空气界面上的反射.Wang 等(2021b)发展了广义的动量守恒定律,并研究了声涡旋波在超表面上的折射/反射.Chen 等(2019a)利用两组离散的阿基米德螺旋缝隙实现了水声涡旋波的聚焦.2015年,阿基米德螺旋声栅结构曾用来生成Bessel 涡旋波(Jiménez et al.2015).最近,Wang等(2021)设计了一种反射超表面来产生空气声Bessel 涡旋波,其中基元为一个上表面带有凹槽的环氧树脂方柱.Jiménez 等(2021)讨论了利用反射超表面实现声涡旋波的聚焦、散焦和扩散.已有的研究结果表明,超表面在基于OAM 的空气(Jiang et al.2018,2020b)或水中(Sun et al.2021)复用通信、类声螺丝刀的扭矩传输(Luo et al.2020)、医疗(Jiménez-Gambín et al.2020)以及声学天线设计(Jia Y R et al.2018,Gao et al.2021)中显示出广阔的应用前景.

4.5 非对称传输

在声波或弹性波的线性理论中,如何实现非互易或非对称传输,例如线性波可以从一个方向穿过系统,但在相反方向受阻的单向传播,是一个具有挑战性的课题并受到越来越多的关注.超表面为人们提供了一种实现非对称传输的新工具.其中一种方法是在声学通道中布置一个或多个折射/反射超表面,如图24(a)(Zhu et al.2015b)所示的典型结构,利用超表面的异常反射实现了非对称传输.Liang Q X 等(2018)利用具有类直井基元的负反射超表面,在理论和数值上实现了开口弯曲通道的非对称传输.Zhu 等(2015b,2015c)利用声反射超表面对调节波的传播方向,在非阻塞通道中实现了非对称传输.Ge 等(2018)借助由钩状基元构建的多个反射超表面设计了一个通风窗,数值和实验结果显示了其非对称传输特性.Wang 等(2016a)和Song 等(2019b)则通过在通道中放置折射超表面以实现非对称传输,其中使用了吸收材料吸收来自一个方向的波.

实现非对称传输的另一种方法是将相位梯度超表面与超材料相结合.图24(b)(Shen et al.2016)所示的组合系统由具有锥形卷曲空间基元的超表面和迷宫基元构成的近零折射率超材料(near-zero-index metamaterial,ZIM) 组成.该组合系统可以实现非对称传输.由于隧道效应,垂直入射的波可以直接通过ZIM,然后通过超表面以预设的角度传播.相反,由于ZIM 的临界角接近零,当波先以一定的倾斜角度通过超表面时,在ZIM 和超表面之间的界面上将发生全反射.人们利用各种基元如锯齿形基元(Chen et al.2018b)和混合共振基元(Jiang et al.2016b,Gu et al.2021)构建的超表面,进行了类似的研究.除了ZIM 之外,具有方向带隙的声子晶体也被用来与超表面一起构建非对称传输结构.以正方形晶格声子晶体为例,当入射波的频率在ΓX 方向带隙范围内时,波在ΓM 方向可以传播,但在ΓX 方向被禁止传播.根据这一特性,已实现了声波(Song et al.2016)和弹性SV 波(Zeng L H et al.2019)的非对称传输.此外,Chen C 等(2020)利用拓扑绝缘体和声学超表面构成的结构在一定频率范围内实现了对称和非对称传输之间的动态切换,其中波传播或全反射取决于边缘态是否被激发.

具有一定距离的两个超表面也可用来实现非对称传输.Liu 和Jiang(2018)通过将图10(a)所示的混合共振基元分成对称的两部分,获得了两个声学相位梯度超表面,它们之间有一个空气间隙.在某个微小间隙宽度 (波长的二十分之一) 和超过临界角入射的情况下,表面束缚模态的波在两个界面处相互干涉,由此在一个方向上产生全反射,从而实现非对称传输.此外,Fu 等(2020b)通过调整两个二元超表面之间的间隙宽度使其超过一定值,实现了非对称波束分裂.Tang S 等(2022)还利用两个二元超表面,生成了非对称自弯曲波,并实现了非对称聚焦.类似地,Cao 等(2018a)利用两个立柱超表面实现了弹性弯曲波的非对称传输.如图24(c)所示,垂直入射到上方超表面 (EWGM1) 的波将被完全反射;而在相反的方向上,垂直入射的波将被下方的超表面 (EWGM2) 重新定向,以确保能够以负折射角度通过EWGM1.Xia 等(2019)利用PZT 贴片设计了一种自适应结构,实现了SH 波的非对称传输.除了单向传播的非对称行为外,人们还利用两个声学超表面实现了单向(Xia et al.2018)和双向(Chen et al.2018a)非对称聚焦.最后值得一提的是,Zhu X H 等(2020)对由两个时空调制薄膜组成的波导系统中的非对称传输问题进行了理论和数值研究.

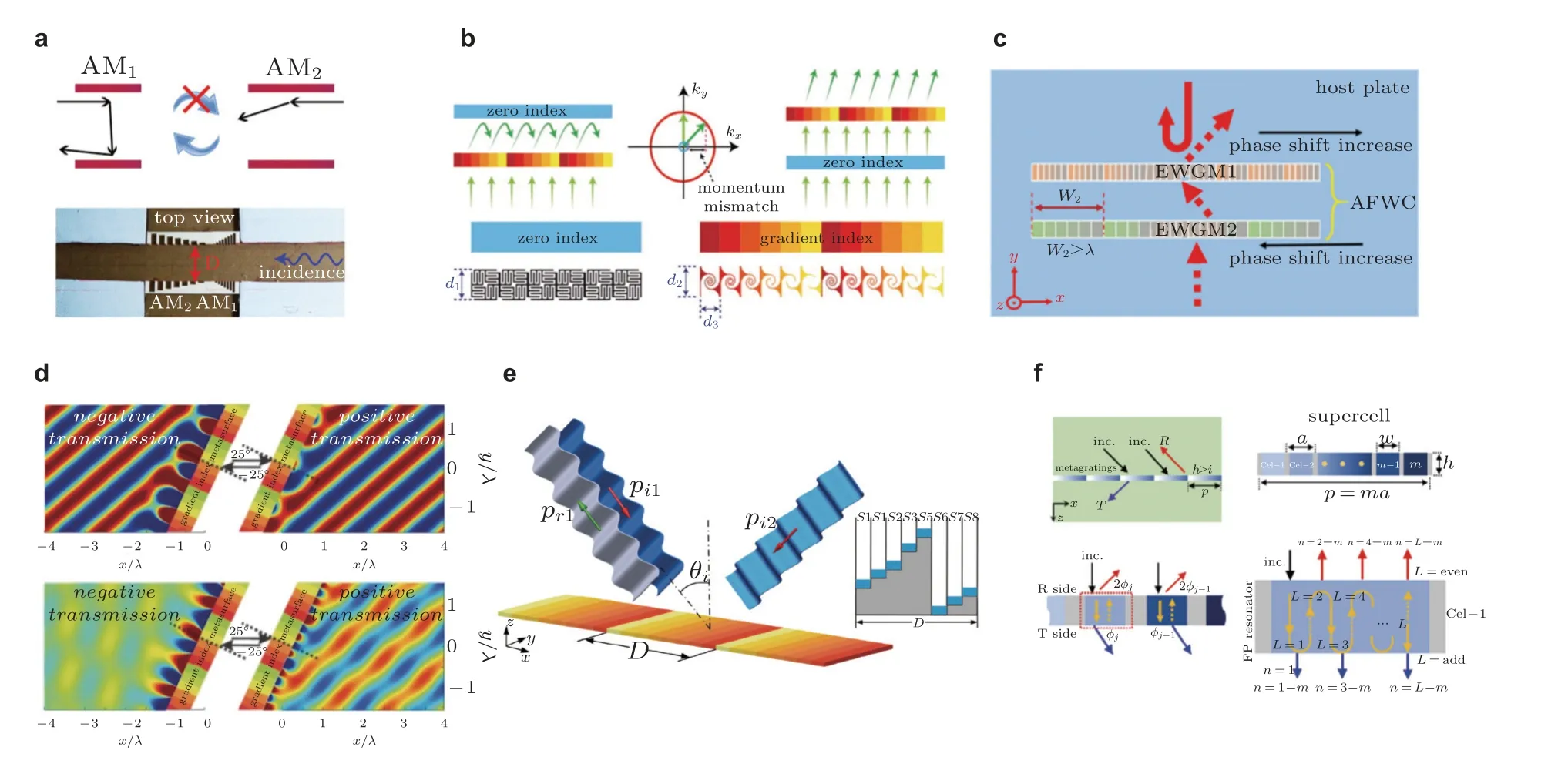
图24 非对称传输的实现.(a)含多个超表面的声通道(Zhu et al.2015b),(b)一个超表面和一个超材料构成的组合体系(Shen et al.2016),(c)两个相位梯度超表面(Cao et al.2018a),(d)单个有损透射超表面(Li et al.2017),(e)单个有损反射超表面(Song et al.2019),(f)考虑整数奇偶性的单个无损超表面(Fu et al.2019b)

当引入损耗 (如黏性或热损耗) 时,仅有一个梯度超表面也可以实现非对称传输.借助固有损耗来抑制高衍射阶,人们设计了由混合共振基元(Li et al.2017)、三层空间卷曲基元(Ju et al.2018)或V 形硬板(Song et al.2020)组成的基于格栅衍射的声学超表面,以实现非对称传输,如图24(d)所示.由于没有多次反射,来自一个方向的波损耗效应引起的衰减将较弱;而对于相反方向,多次反射大大地增强了损耗效应(Ju et al.2018),这将导致非对称传输.另外,将Song 等(2020)提出的有损超表面与声学拓扑绝缘体相结合,Song 等(2021a)实现了频带选择拓扑边缘态的单向传播.

最近,利用单个有损超表面实现的非对称反射受到了关注.如图24(e)所示(Song et al.2019),左侧来波会被完全反射,而右侧入射波则会被完全反射或吸收.这种不对称行为源于倏逝波的非对称激发.其中系统中的损耗是通过将泡沫填入直井基元引入的,如图24(e)右图所示.Wang X 等(2019)和Ju 等(2021)设计了基于格栅衍射的非厄米声学超表面镜面,以实现非对称回射.Wang X 等(2019)使用了凹槽基元,每个周期内只有第一个凹槽基元具有窄缝,以此引入固有损耗,讨论了奇异点的极端非对称反射.另外,Ju 等(2021)还考虑了由两层迷宫基元引入的固有损耗.

有趣的是,当考虑一个超胞中基元数量的整数奇偶性时,单个无损超表面也可以实现非对称传输.如图24(f)所示(Fu et al.2019b),该整数奇偶性可影响在超表面内波的反射次数,从而控制波的衍射阶次.Fu 等(2019b)讨论并实验实现了透射和反射的反转.基于该研究工作,Li B 等(2020)和Fu 等(2020a)分别通过实验实现了兰姆波和声涡旋波的非对称传输.由具有模式选择特性的基元构成的单层无损声学超表面(Qian et al.2020,Tang et al.2021a)也可以实现声波的非对称调制.该基元包含两个相控单胞和一个波导.其中,两个相控单胞具有π 相位差,可以将0阶波模式转换为1 阶波模式;波导则可以阻挡奇数或偶数模式.

更简单地,可以通过周期或准周期分布的非对称散射体或散射体阵列产生的散射波的干涉来实现非对称传播,参见文献(Jia et al.2013,Li C H et al.2014,Craig et al.2019,Fan &Mei 2020,Xu M X et al.2022).但这些研究中不涉及相位梯度.

4.6 声全息

全息术是一种能够记录和再现波场全部信息的技术.声全息显示了广泛的应用前景,如粒子操控(Marzo et al.2015)、声悬浮(Marzo et al.2015)、声捕获(Marzo et al.2015)、成像(Fushimi et al.2021)、医疗(Hertzberg &Navon 2011)、组织工程和机械生物学(Ma et al.2020)等等.然而,声全息通常需要大量的有源相控阵和相移电路,这意味着成本高昂,并限制了其进一步的应用.最近,基于超材料和超表面的声全息技术引起了研究人员的注意,相关研究在光学领域已经相当成熟(Deng et al.2020).图25所示的反射和折射情况下的超表面全息图可以通过仅调制相位或同时调制相位和幅值来实现.Xie 等(2016)利用带有两层亚波长迷宫基元的被动超表面实现了声全息图,避免了繁琐的电路,只需要一个传感器.他们提出的超表面仅提供了相位延迟,而保持了相对恒定的传输幅值,因此,需要结合优化算法来实现.基于纯相位调制,Wang H P等(2019)设计了反射波的超表面全息图,实现了单焦点和多焦点成像.对于水声也有一些基于纯相位调制的研究发表.Melde 等(2016)利用纯相位全息图在实验上获得了水声超声图像.同时,他们实现了对水中固体粒子和空气中液体粒子的超声波操纵(Melde et al.2016).Bakhtiari-Neiad 等(2018)应用迭代角谱方法设计了一种用于水声超声的相移全息图,并利用全息图生成了多焦压力图.Zhang 等(2018b)介绍了一种改进的加权Gerchberg-Saxton 方法,用于单个声全息图的设计,其中同时考虑了幅值和相位调制,实现了水声多焦点聚集和字母“U”声场.Brown(2019)利用两个超表面来调节幅值和相位,在实验上获得了具有均匀幅值的字母“UCL”.相位-幅值调制为全息图提供了更多的设计空间(Zhang et al.2018b,Brown 2019).然而,相位和幅值的耦合给设计带来了困难,通常需借助优化方法.因此,相位和幅值调控的解耦或准解耦设计受到了关注.

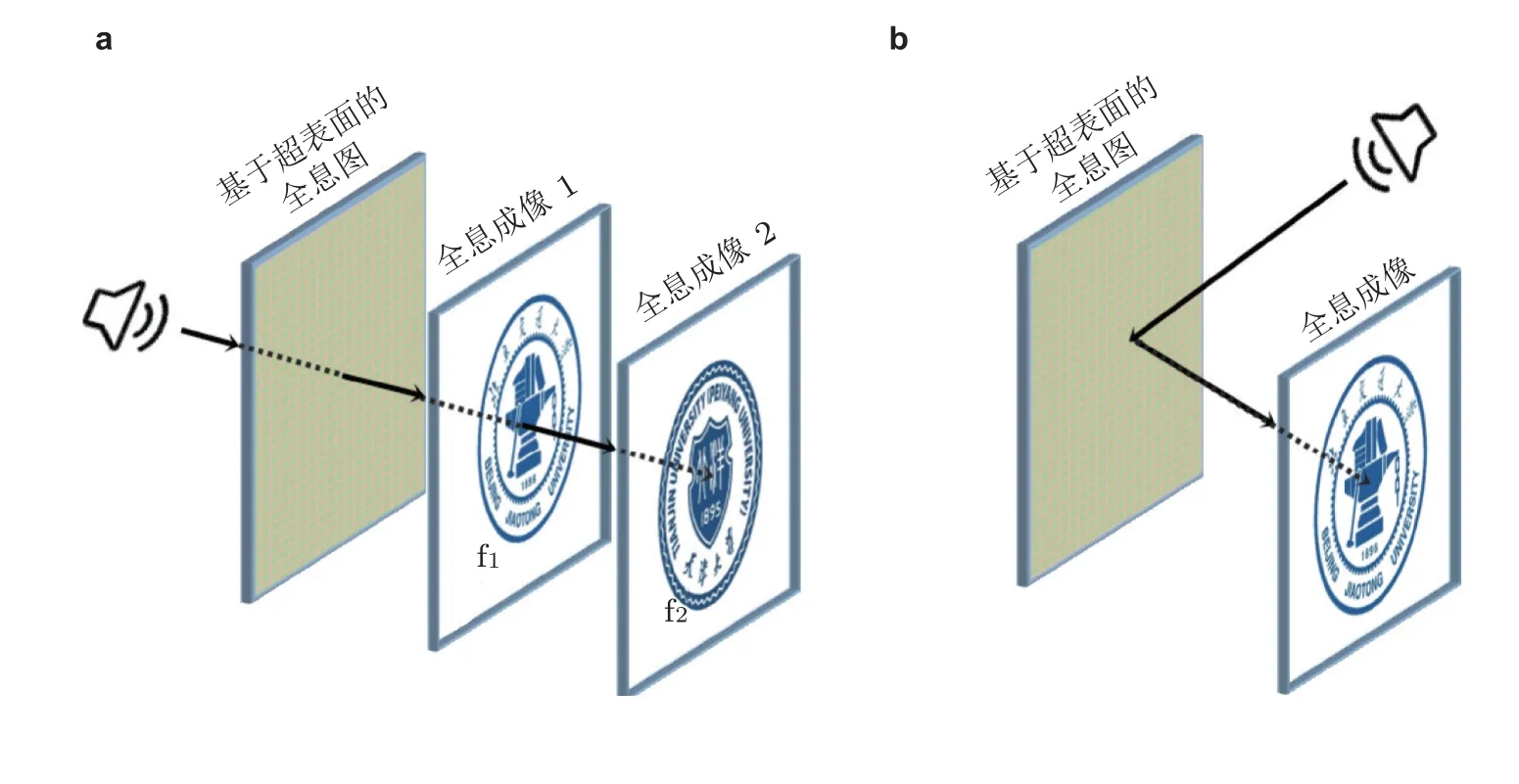
图25 基于超表面全息图实现的声全息.(a)不同频率折射波的多平面成像,(b)反射波声全息

通过设计具有两个可调参数的基元,可以实现相位和幅值的解耦或准解耦调制.如果通过改变两个参数可以独立地调节相位和幅度,那么就能够实现解耦调制;如果调整一个参数可以独立地调节相位或幅值,而另一个参数的改变会同时引起相位和幅值的变化,那么就得到了准解耦调制.根据后者,Zhu Y F 等(2018)和Fan 等(2020c)设计了有损反射超表面来实现声全息,通过调整由基元吸收边界引入的损耗,得到了反射波的准解耦条件.其中,Zhu Y F 等(2018)实验实现了高保真单平面或多平面声全息;Fan 等(2020c)考虑了基元的固有损耗构建了一个超表面,实现了宽频多平面声全息.图20(a)所示的组合基元可以提供相位和幅值的解耦调制,已被用于构建实现多种全息应用的声全息图(Tian et al.2017).另外,还可设计多频率的多路复用全息图.Zhu &Assouar(2019b)提出了一种基于声反射超表面的多路复用全息图,该超表面可以在四个不同的工作频率下生成四重全息图像.其中的功能基元包含四个共振腔,分别对应于四个工作频率;空腔的位置/高度主要用于控制反射波的相位/幅值.根据类似的思路,最近,Zhu 等(2021a)利用图20(c)所示的基元在数值和实验上实现了透射型多路复用全息图,在两个设计的频率下工作效果良好.Zhang 等(2020a)最近简要回顾了有关超表面声全息图的研究进展.

5 可调超表面设计

如上所述,相位梯度超表面因其超薄特性和多功能性而受到广泛关注.但是,绝大多数提出的声学/弹性超表面仅针对特定频率和特定功能设计制造.换言之,工作频率范围窄,功能单一.如果工作频率或所需功能发生变化,则需要重新设计制作超表面,这将导致浪费并限制超表面的实际应用.因此,希望能够如可调电磁波超表面(He et al.2019,Luo et al.2021,Zahra et al.2021)一样,设计可调的声学/弹性超表面.本节将简要评述可调声学/弹性超表面的研究进展.通常有三种方法可以实现可调(Wang Y F et al.2020).第一种是利用基元本身的机械可重构来实现相位梯度超表面的可调性.其次,也可以通过旋转整个超表面或通过改变多个不可调基元超表面之间的距离来实现.最后是利用智能材料,如压电材料、磁机械材料等,通过外加偏场实现基元或超表面的可重构性.

5.1 机械可重构基元

通过基元组件的移动、旋转或填充液体,可以实现基元的机械可重构.这些方法的物理机制是通过可调的声通道长度、腔体尺寸或共振特性来调节相移.

Chen Z 等(2019)设计了一种具有可调混合共振基元的超表面,其中基元由带移动滑块的亥姆霍兹共振腔组成,如图26(a)所示.通过改变滑块的位置,可以调节腔体尺寸,从而实现了宽频带内的全周期相移,并保持高透射.据此同时从数值和实验上实现了可调节的波前定向、聚焦和声源错觉.Zhang 等(2021)设计了一种可重构基元,该基元由一个阶梯截面圆柱腔和一个由步进电机控制的滑块组成,该滑块带有一个动态控制系统,可以改变腔体的尺寸,从而相应地调节反射波的相位.为了简化控制系统,用3×3 个基元组成一个超胞,并接收相同的控制信号.他们从数值和实验上展示了一个由上述超胞组成的主动超表面,用于声波的动态可调聚焦.Gong 等(2019)给出了一个由如图10(a)所示的混合共振基元组成的可调超表面,其中所有亥姆霍兹共振腔位于一条直线上,并可沿超表面自由移动.然后根据所需的相位分布,通过重新调整直通道的宽度来实现可调性.液体填充也可用于实现基元的可重构,但需要外部水泵系统.Tian 等(2019)提出了一种可调混合共振基元,通过填充水改变亥姆霍兹共振腔的腔体尺寸,如图26(b)所示.从数值和实验上设计了具有多种波动调控功能的可编程超表面,包括定向/聚焦/自弯曲声束和声能流开关.Li X S 等(2019)通过将水注入共振基元以改变反射通道的深度来调制反射声波的相位,如图11(c)所示.并利用平直(Li X S et al.2019)和任意弯曲的(Li X S et al.2020)超表面,数值实现了异常反射、聚焦和地表幻像等三维波前调控.Song 等(2019c)利用可重构超表面实现了宽频全方位入射角弧形地毯隐身和平面模仿弧形凸起的地形伪装.图26(c)所示为他们设计的可重构基元,该基元由带注水喷嘴的水槽组成.根据相位补偿原理,可以通过改变水的高度来调节相位.利用这种可重构基元,他们还设计了一个三通道回射器(Song et al.2019a).

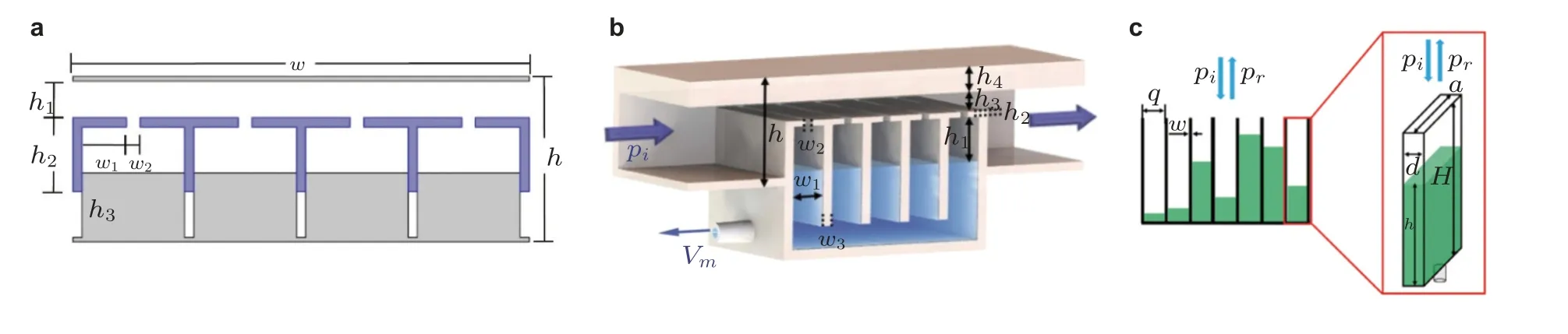
图26 机械可重构基元设计.(a)移动滑块(Chen Z et al.2019),(b)填充水改变腔体尺寸(Tian et al.2019),(c)填充水改变反射通道的深度(Song et al.2019c)

旋转操作是实现基元机械可重构的另一种简单的方法.Wang X L 等(2020)构建了一种扇形可调环状混合共振基元,由外壳和内部固定的圆管组成,如图27(a)所示.通过旋转外壳可以改变谐振器的体积,从而可以连续控制声学相位响应.实现了不同焦点、不同频率下的可调轴向聚焦.Zhai 等(2018)提出了一种带有两个C 形空腔的嵌套结构,如图27(b)所示,用以构建可调的声学超表面.两个空腔之间的环形声通道相当于一个直通道 (如图27(b)中右图所示),其有效长度可以通过旋转内腔来改变,从而可以改变反射相位.利用这种结构,他们实现了高Q 值的谱分离.Zhou H T 等(2020)提出了一种带有可调钩槽的基元,该基元由盖、转子、螺栓和螺母组成,如图27(c)所示.每个转子可以围绕相应的螺栓连续旋转,从而改变钩状通道的有效长度.该基元被用于组装可调的弧形声学超表面(Zhou H T et al.2020)和任意弯曲的超表面(Li X S et al.2021),从数值和实验上实现了地毯隐身和波束自加速.Zou 等(2022)在数值上展示了可调声学超表面的地毯隐身效果,该超表面由可调各向异性共振基元构成,每个基元由一个刚性U形盒组成,其中包含一个具有空间卷曲结构的夹杂物,夹杂物可绕其中心自由旋转.Chiang 等(2020)设计了一种可重构声栅,它由周期性排列的C 形超原子组成,具有Willis 耦合效应.超原子阵列与刚性壁之间的距离为H,如图27(d)所示.通过改变C 形结构的扭转角和距离H,可以获得不同工作频率或不同反射角下声波的高效调控.Li P 等(2020)数值研究了图13(c)所示的由可旋转各向异性三相共振器构成的可调超表面对水声的宽频广角聚焦.Xie 等(2020)提出了一种利用具有嵌套螺旋轨道的声学超表面设计的可调双频带完美吸收器,通过旋转带有扇形孔径的盖子,可以在宽频范围内调节吸收频段.

图27 利用旋转操作实现机械可重构基元和超表面.(a)扇形可调环状混合共振基元(Wang X L et al.2020),(b)带有两个C 形空腔的嵌套结构(Zhai et al.2018),(c)带有可调钩槽的基元(Zhou H T et al.2020),(d)离刚性壁一定距离具有Willis 耦合效应的C 形超原子(Chiang et al.2020)

基于螺丝-螺母工作原理,Zhao 等(2018)提出了一种螺旋基元,如图28(a)所示.当圆柱形螺旋结构基元拧入孔中时,形成螺旋通道,通道长度 (进而相移) 可以通过旋进深度连续调节.他们通过一个圆盘状的超表面,数值和实验上实现了宽频范围内各种空气声源的三维可调聚焦(Zhao et al.2018).Chen 等利用类似的基元,设计了一个平直的(Chen A L et al.2020)和一个弧形的(Chen A L et al.2021)可调超表面,实现了宽频范围内的异常透射、任意点聚焦、声束聚焦、声束自弯曲和源幻像之间的多功能转换.Fan S W 等(2019)设计了一种反射螺旋基元,如图28(b)所示,将匹配的螺旋结构旋转到螺旋通道中以形成反射端,反射波的相移可以通过旋进深度进行调节.利用这种基元,他们在文献(Fan S W et al.2019)中构建了一个用于异常反射、任意点聚焦和声束自弯曲的平直超表面,在文献(Fan et al.2020b)中则构建了一个用于声学隐身和幻像的弯曲超表面.仿照类似思想,Fan 等(2020a)设计了一个由螺旋声通道组成的超表面(图28(c)),并通过将匹配的螺旋结构旋转到不同长度的通道中,实现了可调的多阶声涡旋.在文献(Fan et al.2020c)中,他们提出了一种用于声全息的可调有损超表面.相应的基元如图28(d)所示,由格栅通道和可调内部吸收器组成.内部吸收器通过将匹配的螺旋体旋入螺旋间隙来构造,并且可以作为一个整体沿着通道上下移动.螺旋体的旋转角度和整个吸收器的高度这两个参数是可调的,从而可实现相位和幅值的准解耦调制.螺丝-螺母工作原理也被用于可调弹性超表面的设计.Yuan 等提出了一种可重构鱼骨状功能基元,如图28(e)所示,用于调控弹性弯曲波(Yuan et al.2020a)或平面内波(Yuan et al.2020b)的传输.该基元由六对等长的螺栓和两排作为振子的螺母组成,通过拧入或拧出来改变螺母的位置,可以连续调节透射弹性波的相位,进而可实现多功能转换.

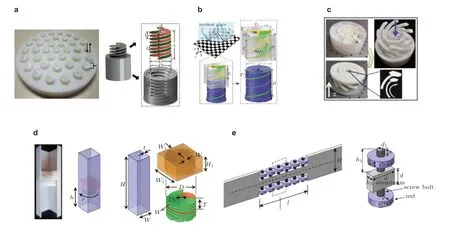
图28 基于螺丝与螺母工作原理的机械可重构基元或超表面.(a)透射型基元(Zhao et al.2018),(b)反射型基元(Fan S W et al.2019),(c)产生声涡旋的超表面 (Fan et al.2020a),(d)具有可调吸收器可实现相位和幅值准解耦调制的基元(Fan et al.2020c),(e)弹性波基元(Yuan et al.2020a)

5.2 调节整个超表面的方位

超表面的可调性也可以通过调整整个超表面的方位 (包括位置和方向) 来实现.在这种情况下,基元本身是不可重构的,但可以通过旋转整个超表面或改变超表面之间的距离来调节功能或工作频率.Li 等(2017)通过旋转整个超表面,实现了特定频率范围和入射角范围内的可调非对称传输,如图29(a)所示.Song 等(2019b)通过在不同方向放置一个超表面而不改变其结构,获得了一个可转换的声通道,该声通道由两个V 形板、吸声材料和一个透射超表面组成.当超表面竖直放置时,可以观察到宽频非对称声传输;若将超表面逆时针旋转45°,则可以实现宽频双向隔声.

此外,还可以通过改变两个平行或共面超表面之间的距离来实现可调.Liu 和Jiang(2018)在两个相同的混合共振基元之间引入了可调空隙,并在空隙宽度的临界值处实现了非对称和对称传输之间的转换.Fu 等(2020b)通过调节两个超表面之间的距离,实现了非对称和对称分波之间的功能转换.类似地,Yuan 等(2015)对可调负折射再聚焦进行了数值和实验研究.结果表明,焦点可以在宽频范围内调节.Xia 等(2018)利用两个平行的超表面,在实验和数值上实现了宽频可调非对称声聚焦,如图29(b)所示.他们发现焦点的垂直和水平位置分别受入射角和两个超表面之间的距离控制.Chen 等(2018a)利用两个具有三层空间卷曲基元的平直超表面实现了双向非对称声聚焦,通过调节两个超表面的距离,可以改变双向非对称聚焦的焦点位置和强度.Tang S等(2022)讨论了类Airy 声束生成/聚焦的非对称和对称传输之间的功能切换.上述系统由两个平行的超表面组成.Chen 等(2018c)通过调节两个共面超表面之间的距离来控制两个类Airy 声束的焦点位置,结果表明: 焦距随距离的增加而增加,但焦距形状不受影响.

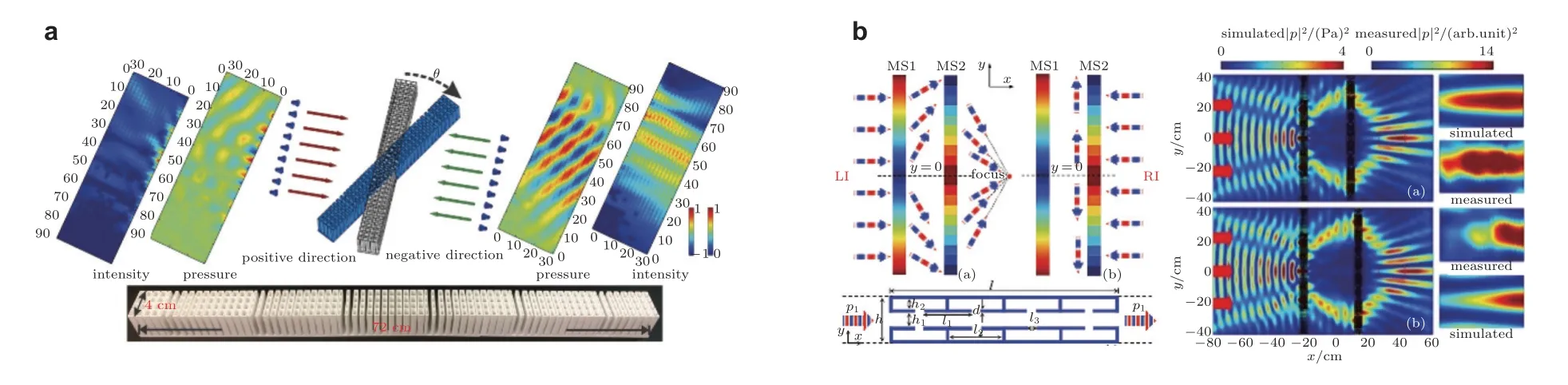
图29 整个超表面的方位调节.(a)旋转整个超表面(Li et al.2017),(b)改变两个平行超表面之间的距离(Xia et al.2018)

5.3 施加偏场

另一种实现超表面可调、主动甚至编程可调的方法是使用智能材料,智能材料的物性可以通过施加偏场进行调节.智能材料,如压电、压磁、软磁、光机械和热机械材料,已被应用于声子晶体和超材料中,通过多场耦合效应可调节或主动调节其能带结构和等效特性 (如等效模量、密度、折射率等).Wang Y F 等(2020)回顾了2020年前关于这一课题的进展.

已有的大多数研究使用具有外部电场或电路的压电材料来实现可调性或可编程性.如图30(a)所示,Popa 等(2015)设计了一种由压电膜组成的基元,压电膜由数字电路控制,可实时重构.超薄超表面由可重构电子模块构建,以实现聚焦、波束控制或双重功能.实验证明,入射波的二次谐波成像突破了衍射极限(Popa et al.2015).其实,这种基元首先被用来主动调节等效材料属性(Popa et al.2013),实现声波的非互易传输(Popa et al.2014).Li S L 等(2021)提出了一种利用压电换能器的自适应反射声学超表面.图30(b)所示为其中的薄膜型基元,该基元由空气腔和铅层组成,铅层两侧带有压电传感器.膜上的张力由施加在压电换能器上的静态电压自适应控制,并沿超表面产生相位梯度.利用这种可调超表面,可以实现异常反射、波聚焦、波束自弯曲和声隐身等多功能转换.Li X 等(2022)提出了一种可调薄膜型基元,该基元通过将五块有一定曲率的带有铝电极的PVDF/聚酰亚胺悬臂梁片插入矩形空腔构成.在PVDF/聚酰亚胺悬臂梁片的铝电极上施加电压,可以改变其曲率半径,进而可调节反射波的相移.利用PZT-5H,Peng 等(2022a)设计了一种可调的宽频超表面,用于调制折射声波,并对异常折射和波聚焦进行了模拟.该基元由一块覆盖PZT-5H 的铜板组成,铜板由两个相同的相对放置的铝壳制成的亥姆霍兹共振腔夹持.其共振频率可通过特定的外部电感器进行调节(Peng et al.2022a),因此可以调制透射波的相位.后来,他们利用类似的结构,通过改变外部电容器,在数值和实验上实现了可调波前调制 (包括波束定向、聚焦和类镊子波束生成) (Peng et al.2022b).利用压电片和环氧树脂基体,Shen 等(2019)设计了一个由16×16 个基元组成的二维主动超表面,如图30(c)所示,用于控制水声.每个基元都使用了多通道电动驱动器来调节压电片的振动,这使得辐射超声的相位和幅值可编程调控(Shen et al.2019).他们对无格栅和旁瓣的任意超声聚焦进行了数值和实验研究.

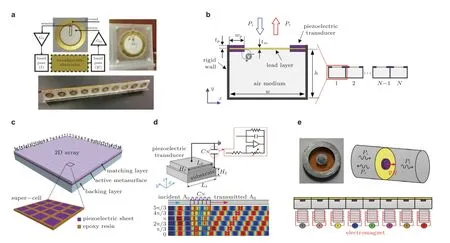
图30 通过施加偏场实现的可调基元和超表面.(a)数字电路控制的压电薄膜基元(Popa et al.2015),(b)由两侧带压电传感器的铅层覆盖的空气腔构成的薄膜型基元(Li S L et al.2021),(c)由压电片和环氧树脂基体所组成的基元构建的主动超表面(Shen et al.2019),(d)由五个基本单胞组合而成的基元,其中每个基本单胞通过在基板上粘贴一个连接负电容分流电路的压电换能器构成(Li S L et al.2018),(e)由电压控制的磁性可调基元和超表面(Chen et al.2017b)

基于压电材料的可调弹性超表面也得到了关注.Li S L 等(2018)通过在基板上粘贴一个连接负电容分流电路的压电换能器构建了一个基本单胞,如图30(d)中的上图所示,用来设计一个可调弹性超表面.如图30(d)中的下图所示,超表面的功能基元由五个基本单胞组合而成,通过改变负电容可以实现覆盖2π 周期的相移调节.他们利用该可调弹性超表面实现了兰姆波的异常折射、聚焦和源幻像.Xia 等(2019)提出了一种类似的可调基本单胞,该单胞在基板两侧有两个PZT 贴片,可以实现不同频率下弹性SH 波的灵活操控;并进一步利用双层超表面实现了非对称波传输.Chen 等(2018)利用在钢板上粘贴由简单数字电路控制的压电贴片构成的自感应-致动单元,通过数值和实验设计了可编程弹性超表面,首次实现了对弯曲波传输的可重构和多功能实时调控.他们通过简单的电路编程,实验实现了包括异常折射、聚焦、波束自弯曲和非对称传输在内的波动实时调控;并通过数值模拟实现了不同多边形孔洞的隐身皮肤功能.

电磁铁的极性可以通过反向直流电压进行切换,也是实现主动、可重构或可调超表面的手段之一.如图30(e)所示,以铁片为中心质量的弹性膜组成的磁可调基元可用于构建磁力调节的声学超表面,其中磁力可由施加在每个电磁铁上的电流控制,如图30(e)中的下图所示(Chen et al.2017b).该文作者设计了一个可调深亚波长超表面(λ/85)用于调制反射波的波前,通过改变磁力,可以切换异常反射、点聚焦和波束自弯曲等多个功能(Chen et al.2017b).最近,基于上述基元设计,Liu P 等(2020)提出了一种用于构建透射超表面的双层膜基元,可以实现聚焦、分束和其他近场声学显示之间的切换.Ma G C 等(2018)利用电磁铁设计了一种二元空间声音调制器,可通过调制相位在混响环境中产生安静和喧嚣区域.此外,基于磁-机械耦合效应,磁致伸缩材料也可用于实现超表面的可调设计.Zhang S Z 等(2022)设计了一种立柱式磁弹性超表面,实现了弯曲波的可调异常折射.通过改变施加在磁致伸缩立柱基元上的磁场和预应力,可以调节相移和透射系数.

6 数字编码超表面

上述讨论涉及相位梯度超表面,该类超表面通过定制沿超表面的相位分布来调制波前.最近,在电磁波领域提出了一类称为数字编码超表面的新型结构(Cui et al.2014,Giovampaola &Engheta 2014,Gao et al.2015),它只包含幅值相同相移不同的几种 (通常是两种) 组分单元,作为熟知的布尔数或逻辑位.如果超表面由两种具有相反相位0 和π (分别对应逻辑位0 和1) 的单元组成,则称其为1 比特编码超表面.包含0,π/2,π 和3π/2 四种相位组态 (分别对应逻辑位“00”“01” “10” “11”) 的组分单元的超表面称为2 比特编码超表面.类比推广,n比特编码超表面包含2n个逻辑位,相位间隔为2π/2n.编码超表面一般基于惠更斯-菲涅耳原理,通过按适当顺序排列组分单元来实现波前调制.即超表面上的每个单元都可以被视为次级波源,总场是这些次级波源产生的所有波的叠加,如图2所示.例如,考虑如图31(a)所示的1 比特编码超表面,其包含M×N个大小相等的单元,每个单元 (0 或1) 占据一个尺寸为L的晶格.于是根据惠更斯-菲涅耳原理,平面波垂直入射时,透射波的远场模式可表示为(Cui et al.2014,Xie et al.2017b)

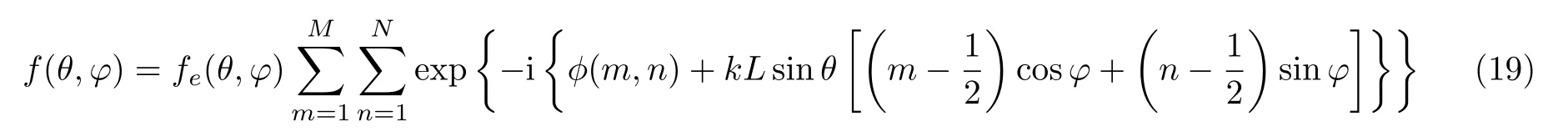
其中θ和φ分别为任意方向的仰角和方位角;ϕ(m,n) (=0 或π)是第m行n列晶格的散射相位;fe(θ,φ)为晶格的模式函数.上式表明,散射远场模式f(θ,φ)可以通过改变单元0 和1 的排列进行调节.

2016年,Fan 等(2016)将商用试管制成的两种基元按不同顺序排列,展示了宽频声聚焦和声针,其中带盖和不带盖的试管分别产生0 和π 的相移.值得指出的是,他们提出的平面结构实际上是一个编码超表面,尽管他们没有指明.2017年,Xie 等(2017b)将编码超表面的概念扩展到声波,设计并制作了一个二元 (1 比特) 编码声学超表面,其逻辑位为“0”和“1”,如图31(b)所示,实现了透射声波的波束分裂和聚焦.采用类似的设计,Xie 等(2017a)利用不同的编码序列,从理论和实验上实现了多频段非对称传输.Cao 等(2019)对声学反射超扩散器进行了数值研究,其中每个基元由刻于固体板上的3×3 个相同的阶梯形空腔构成,具有不同空腔尺寸的基元用于逻辑位0 和1.Chen 等以空气基元作为逻辑位0,以外形尺寸相同的空间卷曲基元作为逻辑位1,设计了一个1 比特编码超表面生成类Airy 波束(Chen et al.2019b),并实验实现了宽频波聚焦(Chen D C et al.2020).Li W B 等(2020)和Zhang N L 等(2022)分别以螺旋结构(Li W B et al.2020)或将螺旋结构与空气腔组合(Zhang N L et al.2022)作为逻辑位1,设计了1 比特编码超表面,在实验上实现了折射波(Li W B et al.2020)和反射波(Zhang N L et al.2022)的二维波聚焦和分束.Li W B 等 (2020)还用遗传算法实现了三维波聚焦.为了在较宽的频率范围内设计具有高阻抗匹配的紧凑编码超表面,Fang 等(2019)以两种喇叭状螺旋结构作为逻辑位1(π) 和1/2(π/2)与空气基元(0)结合,通过打破逻辑位0 和1 的空间对称性,实现了无旁瓣的声束分裂;并针对异常折射,设计了包含逻辑位0 和1/2 的非对称编码超表面.Zuo 等(2019b)利用1 比特编码超表面实现了声学图像的可控投影、加密/解密.他们使用的基元是如图31(c)所示的组合基元,由空间卷曲结构 (相位调制器) 和直通道 (幅度调制器) 组成.该基元表现出波传播的非对称特性,正反两个方向放置分别代表逻辑位0 或1,如图31(c)所示.基于无反射双各向异性特性,Su和Liu(2020)提出了一种幅值调制的二元超表面,其由两个具有透射幅值调制功能的亥姆霍兹共振基元组成,可实现完美的异常折射.Zhang Y 等(2020)和Song 等(2021b)利用亥姆霍兹共振基元设计了频率选择编码超表面.Zhang Y 等(2020)选用可在两个特定频率下产生不同相位响应的四种编码单胞做为逻辑位0 和1,并通过数值和实验展示了异常反射、声波扩散和Airy 波束的生成.Song 等(2021b)考虑了热黏性损失,通过调整出射衍射模式的数量,获得了理想的负反射.此外,Tang 等(2018)结合中国剪纸艺术,提出了一种超薄 (最薄达λ/650) 镂空图案声学超表面,实现了声涡旋 (Fermat 螺旋图案)、聚焦 (条纹图案) 和超振荡 (Penrose 状图案).其中多孔软聚合物纤维/刚性珠网络组成的超薄薄膜可以使折射波产生π 的相移,从而能够在不进行空间离散的情况下构建超薄编码 (1 比特) 超表面(Tang et al.2018).基于相同的设计理念,他们提出了曲面 (包括球面、锥面和任意弯曲) 超表面,用于透射声波的聚焦(Tang H C et al.2019).另外,他们还将该图案设计成锥形表面,构建了一个伞形结构,用于焦距实时可调的声聚焦.

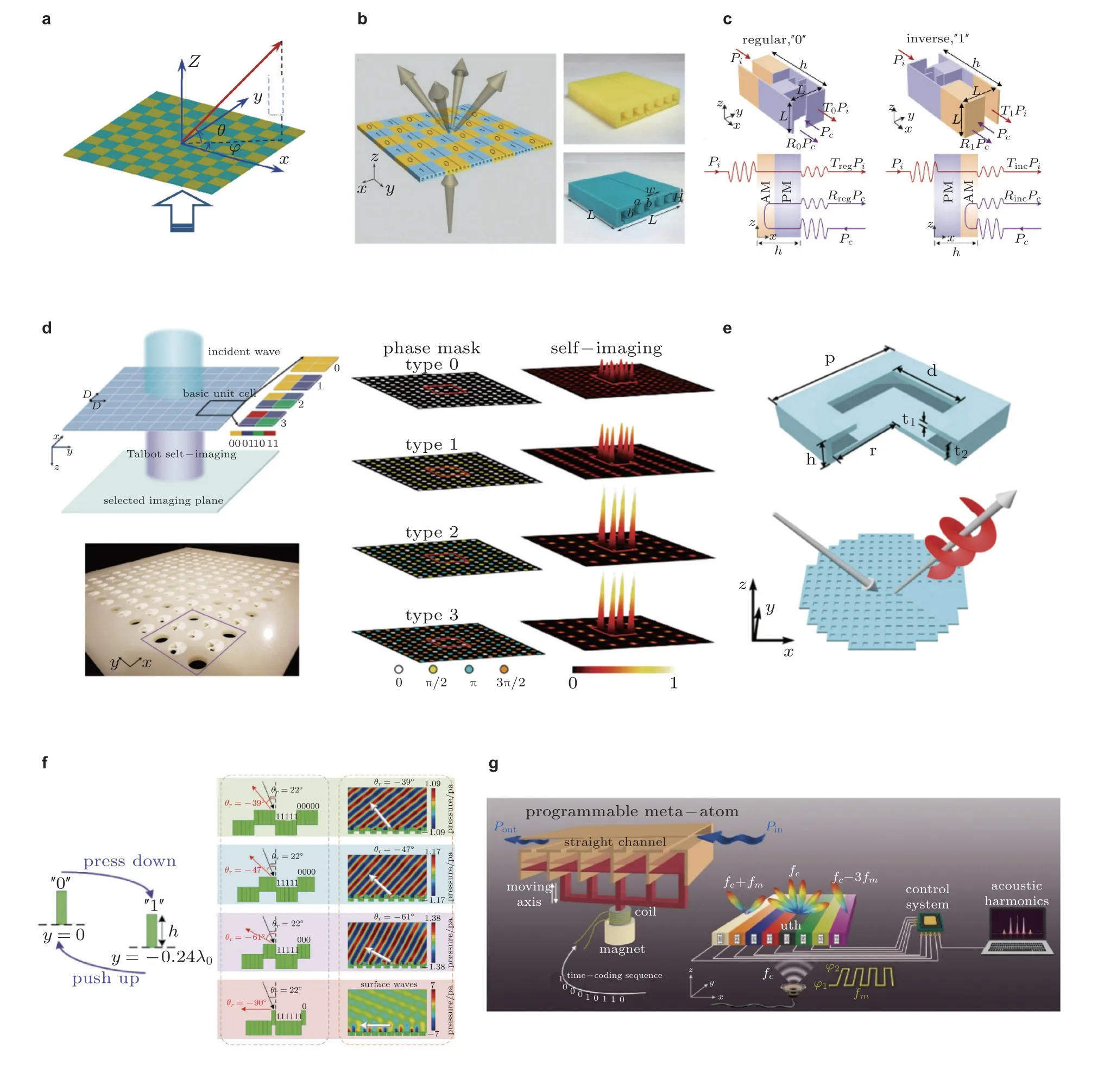
图31 数字编码超表面.(a)平面1 比特编码超表面的远场调控示意图,(b)编码位0 和1 组成的超表面实现波束分裂功能(Xie et al.2017b),(c)以正向或反向排列用作逻辑位0 或1 的非对称基元(Zuo et al.2019b),(d)用于Talbot 自成像的无相位调控 (0 型) 和有相位调控 (1-3 型) 的编码声学超表面(Gao et al.2020),(e)由亥姆霍兹共振基元构建的产生涡旋波的反射型3 比特编码超表面(Zhang Y et al.2019),(f)可调1 比特编码超表面(Zuo et al.2019a),(g)机电可编程声学数字编码超表面(Fakheri et al.2021)

波的调制也可以通过由两个相位相差π 的基元交替周期性排列组成的编码超表面来实现.例如,Fu 等(2019a)利用由空气基元和空间卷曲基元 (图9(a)) 组成的1 比特编码超表面实现了高效的准回射、三通道回射和镜面反射.按照类似的思路,Zhu 等(2019a)实现了完美异常反射.他们还设计了一个折射型二元超表面,含有空气基元和改进的空间卷曲基元 (图8(d)),实现了声波的完美异常折射(Zhu et al.2019a).Chen S 等(2021)使用由两个空间卷曲基元 (图9(a)) 构成的1 比特编码超表面,实现了宽角度入射声波的高效异常反射.

上述1 比特编码超表面降低了设计和制造的复杂性.但是,2 比特和多比特编码超表面具有更大的自由度来调控波的传播,并且可以实现更复杂的功能,例如,生成涡旋波.Gao 等(2020)提出了一种用于Talbot 自成像的被动2 比特编码声学超表面 (如图31(d)所示),并实验实现了灵活的远场声波再分布和增强.Zhao 等(2022)采用基于从下至上的拓扑优化方法设计的1 比特和2 比特编码超表面,数值和实验上实现了透射声波的宽频声天线、聚焦和散射扩散.Zhang Y等(2019)证明了由亥姆霍兹共振编码单元组成的多比特声学编码超表面 (包括1 比特、2 比特和3 比特) 可生成多个波束 (1 比特)、异常反射 (2 比特) 和涡旋波束 (3 比特,如图31(e)所示).Bai等(2019)利用开口金属环谐振器设计了多比特超表面,以同时操控反射的电磁波和声波.分别利用1 比特、2 比特和3 比特多物理场编码超表面实现了散射扩散、多波束控制和涡旋波束生成.

可调编码超表面也受到关注.Zuo 等(2019a)提出了一种可调的1 比特编码超表面,它由一系列矩形条片组成.如图31(f)中的左图所示,通过上推或下压操作,每个条片可以做出逻辑位0 或1 的响应.通过调整编码序列,他们实现了不同方向上的完美负反射,并且抑制了镜面反射,参见图31(f)中的右图.Fakheri 等(2021)提出了一种时空数字编码声学超表面,该超表面可进行机电编程,如图31(g)所示.当编码序列在空间和时间维度上排列时,可以在一个或多个频率上精心编程实现各种散射功能.Cao W K 等(2021)提出了一种由类亥姆霍兹共振腔数字编码单元组成的可调3 比特编码超表面,以实现声波的三维调制.其中的基元包含3×3 个相同的阶梯形圆柱腔,其深度由单个电机控制.四个基元构成一个数字编码位.借助电机和相应的控制系统,可以改变活动柱塞的位置,以调整反射波的相位.

编码超表面是一个相对较新的研究课题,目前尚处于开始阶段.关于水声和弹性波的编码超表面研究仍然很有限.最近,Yu 等(2021)设计了一种带有直井基元的2 比特编码超表面,以实现宽频水声隐形.Li X S 等(2022)提出了用于弯曲波分波和聚焦的稀疏1 比特弹性超表面,其中逻辑位0 为裸板,逻辑位1 的构型则使用拓扑优化方法反算.Yaw 等(2021)利用分流堆叠压电片构建了一种3 比特主动弹性编码超表面,实现了弹性波的异常折射和任意聚焦.

7 展 望

本文综述了声学/弹性相位梯度超表面的研究进展,包括设计原理、功能基元设计、波动控制的实现、可调和数字编码超表面等.总体来说,这是一个仅出现了十年左右的课题,从概念、机理、设计方案、可调性直到实际应用,许多具有挑战性的问题,都亟待解决.

7.1 设计原理的改进

广义斯涅尔定律是超表面设计中广泛使用的原理,已针对各种情况,从二维到三维(Li X S et al.2019),从平面到曲面(Li X S et al.2020)等,得到较充分的研究.但是,表面阻抗理论尚未得到充分的关注.大多数已发表的有关表面阻抗理论的研究工作都集中于二维情况下平直超表面的异常反射/折射.该理论有待扩展到三维、弯曲超表面和复杂波前调制 (如聚焦、波束自弯曲、涡旋) 等情况(Li J F et al.2019,Peng et al.2021,Xie &Hou 2021).此外,适用于L 波和T波混合模式的弹性矢量波表面阻抗理论是一个值得研究的课题,这将为精确控制弹性波在固体中的传播提供强有力的工具.

7.2 水声超表面

空气声超表面已经受到广泛的关注.但是,关于水声的研究还很有限.水与固体结构之间的动力相互作用非常强,因此应考虑固体的变形.也正是由于这种水-固体耦合效应,两个相连功能基元之间的动态相互作用在超表面设计中起着重要作用(Zhou et al.2021a,2022).如何抑制这种相互作用以实现独立或局部设计是一个挑战性的问题(Zhou et al.2022).反之,也可以利用这种相互作用来设计高效的非局部超表面(Zhou et al.2021a).此外,除了水声,超表面对重力水波的调制也是一个有趣的课题(Sun et al.2016).

7.3 弹性波超表面

与流体中的声波不同,弹性固体中传播的波有各种模式,如体波 (包括P,SV,SH 模式)、表面波、界面波、弯曲波、兰姆波、扭转波等.这对超表面的设计提出了挑战,包括基元设计和设计原理 (如前面提到的表面阻抗理论).尽管弹性相位梯度超表面受到越来越多的关注,但仍有许多问题需要考虑,例如,弯曲超表面、超薄设计(Jiang M et al.2022)、非厄米超表面(Wang X et al.2019)、非对称传输的奇偶性设计(Fu et al.2019b)、编码超表面(Yaw et al.2021,Li X S et al.2022)、涡旋波束生成(Chaplain &De Ponti 2022)、全息等.特别是,有些弹性波模式是耦合的,例如,P 和SV 模式(Yuan et al.2020b).如何设计相位梯度超表面以实现耦合L 波和T波的独立和精确调制或这两种模式的相互转换,应该是一个有趣的课题(Yang X W et al.2019,Lee et al.2020,Lee &Oh 2020,Zheng et al.2020,Dong et al.2022b).此部分相关研究的一个重要内容是设计能够同时调制相位和幅值,甚至可以实现波模式转换的功能基元.

7.4 跨介质传输调控

用于调节声波/弹性波跨越不同介质传输的相位梯度超表面很少受到关注.众所周知,在两种不同介质 (例如空气和水、水和固体或空气和固体) 之间的界面上,阻抗失配可能非常大,从而导致极低的透射率.设计用于调控波高效地跨越不同介质或不同物态传输的超表面已开始受到关注,但大多数研究集中于提高透射率,而没有考虑相位调制(Noguchi et al.2015,Zhang et al.2016,Bok et al.2018,Cai et al.2019,Lee &Iizuka 2020,Park et al.2021).如何构造具有高透射率并可调制相位的超表面是一个有趣且有挑战性的课题(Lee et al.2021).

7.5 可调超表面

可调超表面的研究已取得若干进展,但与可调声子晶体和超材料不同(Wang Y F et al.2020),特定的功能实现需要精确的相移分布,这使得调节相位梯度超表面更为困难.通常,每个基元都应该能独立地调节,这使得可调性很难实现.因此,需要探索新的可调机制和方法.剪纸或折纸已用于可调超材料的设计(Zhang X et al.2022),也可用于可调超表面的设计(Tang H C et al.2019).软材料或柔性结构在机械载荷作用下容易变形,该特性有助于用来设计可重构的超表面.而且,柔软的超表面可以很容易地适应物体的不规则曲面形状.

7.6 编码超表面

编码超表面是一个新兴的课题,有许多亟待研究的问题.例如,关于弹性编码超表面的研究相对较少,仅有不多的文献涉及了单一模式的波(Yaw et al.2021,Li X S et al.2022).适用于L 波和T 波耦合模式的弹性编码超表面尚未受到关注.能否设计出同时调制L 波和T 波的数字比特基元？其他值得注意的课题还有曲面编码超表面的设计、编码超表面数字编程的实现等.

7.7 宽频和频率选择设计

宽频超表面的设计一直是一个受到广泛关注但又非常困难的问题.作为可能的解决方案之一,可通过调整功能基元的结构几何和/或材料特性,对超表面进行可调设计,以在不同频率下获得同样的响应.然而,在宽带脉冲入射的情况下,这种方法不再适用(Zhou et al.2021b).为了调制包含多阶谐波分量的非简谐波或控制瞬态波,使其在宽频率区域产生同样的响应,就需要设计被动超表面(Dong et al.2022a).与之相反的是可在不同频率下实现不同功能的,即具有频率选择性 (频率编码) 响应的被动超表面(Rong et al.2020).宽频或频率选择性被动超表面的设计并不容易,优化方法为这一具有挑战性的问题提供了可能的解决方案(Rong et al.2020,Dong et al.2022a).

7.8 逆向设计

针对特定功能的定制化超表面设计在实际应用中很有吸引力,但很难通过基于经验的设计来实现.基于拓扑优化的逆向设计方法已被应用于设计定制化的局部超表面,其中每个功能基元都是单独优化设计的(Ahn et al.2019,Rong &Ye 2020,Rong et al.2020,Noguchi and Yamada 2021,Dong et al.2022a,Zhou et al.2022).但是,对于非局部超表面,必须协同优化设计一系列基元,这可能产生巨大的计算成本,尤其是在需要大量基元的情况下.也许人工智能,例如机器学习 (或将其与优化方法结合) (Weng et al.2020,Ding et al.2021,Donda et al.2021,Lin Q et al.2021)可能会为我们提供一种有力的工具,因而会在不久的将来受到越来越多的关注.此外,可调或可重构超表面的四维逆向设计将成为一个广受关注的课题.

7.9 应用

声学/弹性相位梯度超表面的应用探索是一个长期的课题,一直吸引着科学家和工程师的兴趣.这些应用包括但不限于: 高分辨率声全息成像、粒子操纵 (例如悬浮(Xu et al.2021,Dong et al.2022a)、声镊/螺丝刀(Ozcelik et al.2018,Zhou Q X et al.2020,Zeng L S et al.2021)和粒子移动(Cai et al.2020))、能量收集(Yuan M et al.2018)、传感器和换能器(Hur et al.2022)、无损检测、声源定位和识别(Gu et al.2020)、混响声控制(Wang et al.2022)、具有波前调制功能的通风隔音窗(Miyata et al.2018;Ge et al.2018,2019;Kumar et al.2020)、声学通信(Shi et al.2017)、声学信息存储和安全保护(Zuo et al.2019b)、声学模拟计算(Zuo et al.2017,2018a,2018b)等.

除以上提到的这些方面,还有其他一些值得关注的课题,例如: 低频或超薄超表面的设计、非厄米超表面的设计(Wang X et al.2019,Ju et al.2021)、超表面对非线性声波 (包括高阶谐波和孤立波) 的调制(Guo X X et al.2018,2019)、同时调制反射波和折射波(Koo et al.2016,Tang Y G et al.2022)、同时控制不同类型的波 (如声波和弹性波或声波和电磁波(Bai et al.2019)) 等.总之,声学/弹性相位梯度超表面的研究方兴未艾,需要物理学、力学、材料、信息、生物医学等领域的科学家和工程师们付出大量的努力.

致 谢国家自然科学基金 (11972246,11872101,12021002,11991031,12122207 和12072223) 资助项目.