近场动力学在断裂力学领域的研究进展

张 恒 张 雄 ,* 乔丕忠

1 清华大学航天航空学院,北京 100084

2 上海交通大学海洋工程国家重点实验室和船舶海洋与建筑工程学院,上海 200240

1 引 言

断裂力学问题一直是力学领域的研究难点.传统基于连续介质力学的理论和数值方法在求解此类非连续问题时遇到挑战.根源在于,连续介质力学建立在连续性假设和局部接触原理的基础上,运动方程中存在着体现内力的位移空间导数项.然而断裂问题中裂纹尖端区域的位移场不连续,空间导数不存在,意味着连续介质力学的基本运动方程构建失效.经典断裂力学理论,定义能量释放率和应力强度因子等概念表征裂纹区的应力集中和变形状态,为断裂问题研究奠定了坚实的理论基础.但传统断裂力学依然建立在连续介质力学框架下,其理论分析仅可求解简化的特定问题;而借助的有限单元法为代表的数值方法仍然面临网格依赖性等困难.

近场动力学 (peridynamics,PD) 是Silling 博士2000年提出的一种非局部理论,非常适用于求解断裂损伤等非连续问题 (Silling 2000,Silling &Lehoucq 2010,黄丹等2010,乔丕忠等 2017,顾鑫等2019,Madenci et al.2022).近场动力学基于非局部内力积分思想,将连续介质力学微分方程转化为积分方程,避免了非连续区局部空间导数不存在等问题.利用统一数学框架描述空间连续与非连续,近场动力学模型可自然模拟裂纹的萌生、扩展与分叉等断裂行为.总的来说,近场动力学理论由两大基础组成: 近场动力学本构力模型和近场动力学键失效模型.近场动力学本构力模型反映了内力与变形的响应关系,具体体现在物质点之间长程作用力的形式,反映了材料的物性信息.近场动力学键失效模型定义和判定了物质点之间长程力的连接状态,是近场动力学量化断裂分析的基础.另外,按照本构力模型的求解形式,近场动力学模型可具体划分为键基近场动力学 (bond-based PD)、常规态近场动力学 (ordinary state-based PD) 和非常规态近场动力学 (non-ordinary state-based PD).对于键基近场动力学模型,节点之间的长程作用力仅与节点对本身的变形量有关;而态基模型的节点内力由该节点近场范围δ内所有节点的状态决定.同时如果节点内力矢量与节点对相对变形方向相同,称为常规态模型;否则称为非常规态模型.

本文首先以弹性材料为例,简要介绍近场动力学本构力模型,之后将系统总结近场动力学的键失效模型以及特定断裂力学问题的研究进展,包括断裂参数求解、混合型裂纹、弹塑性断裂、黏聚力模型、动态断裂、材料界面断裂和疲劳裂纹扩展等,最后对断裂问题的近场动力学研究做进一步展望.

2 近场动力学本构力模型

在近场动力学理论中,连续的材料和结构体被等效离散为带有体积和质量的物质节点.每一个节点受到其近场范围δ内所有其他节点的共同作用,节点之间通过 “近场动力学键” 连接.对于基于状态的近场动力学模型,节点之间的长程作用力不仅与节点对本身的状态有关,还与该节点近场范围δ内其它节点的状态有关.如图1所示,在常规态近场动力学理论中,对于线弹性物质节点x,其运动方程、应变能密度以及力矢量密度表达式可以表示为

图1 常规态近场动力学模型.

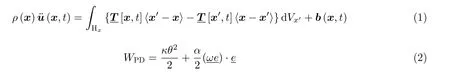
式中,ρ为节点x的密度,u为t时刻的位移,b(x,t) 为体力,x′为x邻域Hx内的任一节点;ξ=x′-x为键矢量,〈ξ〉为初始矢量,=y-y′为变形矢量,[x,t]和[x′,t] 分别为节点x和x′力矢量密度状态;[] 中表示该状态所属的空间和时间,〈〉表示该状态作用或映射的对象,κ和α为近场动力学弹性参数,为影响函数,为键的伸长量,(·) 为近场动力学积分运算符号,为体积加权量,θ为体积膨胀量,t为力密度函数.对于常规态近场动力学模型,节点之间作用力矢量与节点对相对变形方向相同,同时变形场可以分解为体积膨胀和剪切变形.利用近场动力学和连续介质力学弹性应变能密度对应项等效的方法,可推导得到模型中弹性参数.不同维度下常规态近场动力学本构力模型的力密度函数、体积膨胀量及其弹性参数如表1所示(Silling et al.2007,Zhang H &Qiao 2020a).

常规态近场动力学模型中应变能密度和力密度函数均可分解为体积变形和剪切变形对应项,无需附加项.此外,Le 等 (2014) 推导了带有附加项的二维常规态近场动力学模型;Madenci 和Oterkus (2015,2016) 利用特定形式的影响函数建立了近场动力学弹性模型,它们均为表1中模型的等效形式.另外,选取固定泊松比值和特定影响函数,常规态近场动力学模型可以退化为键基近场动力学模型,即键基模型是态基模型的特殊形式,态基模型消除了键基理论对于材料属性的限制 (Silling et al.2007).

表1 不同维度下常规态近场动力学弹性本构力模型

3 近场动力学的键失效模型

3.1 近场动力学断键准则

断键准则定义和判定了物质节点之间作用键的连接状态,是近场动力学量化断裂分析的基础.目前,应用最广的近场动力学断键准则为临界伸长率和临界能量密度模型.其中,基于临界伸长率的断键准则可以表示为 (Silling &Askari 2005,Zhang H &Qiao 2018a):

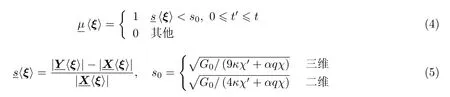
式中,用来表征键的连接状态,s为键伸长率,s0为伸长率的临界值,G0为材料的临界能量释放率,κ和α是表1中给出的常规态近场动力学弹性参数,χ′和χ是与近场范围δ和影响函数相关的参数 (Zhang H &Qiao 2018a,2020a).根据临界伸长率准则,当键伸长率s超出其临界伸长率s0时,节点对之间的相互作用将会永久消失,也就意味着“键”的失效.对于常规态近场动力学模型,临界伸长率s0由断裂能等效得到,即裂纹扩展单位面积释放的能量 (材料的临界能量释放率) 等于所有通过该单位面积键的伸长率达到其临界值所消耗的总能量.如式 (5) 所示,常规态近场动力学模型的临界伸长率是材料弹性参数、断裂参数以及近场范围的函数.此外,若考虑键基模型对材料泊松比的限制并选用特定的影响函数,临界伸长率表达式可退化为键基形式(Silling &Askari 2005,Ha &Bobaru 2010).

临界能量密度断键准则可以表示为 (Foster et al.2011)

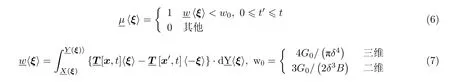
式中,w为键能量密度,w0为键能量密度的临界值,B为二维模型的厚度.与临界伸长率不同,临界能量密度仅与断裂参数临界能量释放率G0以及近场范围δ有关,与材料的弹性参数无关.因此,键基和态基近场动力学模型的临界能量密度形式相同,且该形式适用于弹性和塑性等不同属性材料.

另外,在非局部理论近场动力学模型中,宏观上的裂纹体现为特性区域近场动力学键的失效.为了追踪裂纹的扩展路径,节点变量局部损伤d定义为

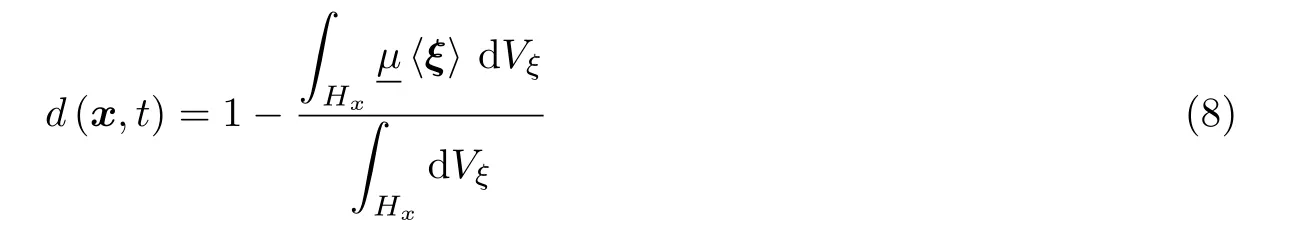
当d=0 时,节点没有断键;d=1 时,与该节点相连的键完全断裂.这样参数d就可用于宏观上观测每个节点的损伤程度,从而追踪裂纹的扩展路径.不需要显式的裂纹面,宏观上裂纹的萌生和扩展由节点失效键的堆积构成.

3.2 材料强度相关的失效模型

材料强度体现了连续场变形中物质点的承载能力,是材料结构失效评判的重要参数.对于涉及强度分析的非奇异结构破坏问题,基于断裂力学理论的断键准则面临着困难.这是因为,上述临界伸长率和临界能量密度均为离散化参数近场范围δ的函数,它们随着网格的细化而不断增大 (Silling &Askari 2005,Foster et al.2011).临界伸长率甚至会大于材料的最大拉伸应变,这在材料强度分析中显然是不合理的.等效于最大拉应变的概念,基于材料拉伸强度的临界伸长率可表示为:s0=σ0/E,它是与网格尺寸无关的材料固定参数 (Gerstle et al.2005).基于类似的强度概念,Tsai-Hill 和Mohr-Coulomb 强度准则被引入非常规态近场动力学模型中,分别应用于复合材料和岩石材料的破坏行为分析 (Wang Y T et al.2016,Hattori et al.2018).然而基于强度理论的失效模型显然不适用于材料的量化断裂分析.

为统一基于强度和断裂理论的临界伸长率表达式,Gerstle 等 (2005) 将近场范围δ定义为材料属性相关的特定值,采用拉伸强度和临界能量释放率得到了数值相同的临界伸长率,然而特定δ对不同尺寸结构的离散化策略提出挑战.Stewart 和 Jeon (2019) 提出了一种双层判定细化叠加技术,将近场动力学键划分于均匀应力场区或者应力集中区,分别使用基于强度和能量的临界伸长率,消除了网格尺寸对材料强度的影响,分析了无损线性杆与带裂纹平板的临界破坏载荷.此外,Zhang H 和 Qiao (2018b) 建立了一种同时考虑材料强度和能量释放率的近场动力学混合破坏模型,引入了有限长度裂纹断裂力学方法,分析了带椭圆孔和中心裂纹平板的拉伸问题,预测了带孔平板从结构强度失效、裂纹萌生到裂纹扩展的破坏过程.Wang Y W 等 (2021) 建立了自适应的近场动力学和连续介质力学耦合模型,利用材料强度准则进行连续介质力学到近场动力学求解方式的转换判定,模拟了狗骨式结构和L 型平板强度失效、裂纹萌生和扩展的失效全过程.

严格来说,裂纹萌生区域材料的内力与变形为非线性关系,为更精确地分析失效过程中材料的强度和断裂行为,需建立近场动力学损伤或塑性模型,分析裂纹尖端材料的非线性变形.Macek和 Silling (2007) 研究了弹塑性材料的近场动力学微塑性模型,给出了与材料强度相关的近场动力学键屈服伸长率,考虑了键达到屈服伸长率之后的塑性变形.此外,黏聚力模型也是一种常用的非线性断裂力学分析方法.弹塑性裂纹以及黏聚力模型的近场动力学研究将在下一章具体介绍.

4 断裂问题的近场动力学研究

4.1 断裂力学参数

能量释放率、应力强度因子和J 积分为表征裂纹尖端实时状态的重要参数,是经典断裂力学理论的基础.在近场动力学理论框架下求解能量释放率、应力强度因子和J 积分,为同时发挥近场动力学和传统断裂力学的优势提供了可能.

能量释放率的断裂力学求解方式主要包括: Griffiths 能量释放率定义、虚拟裂纹闭合技术和J 积分,它们也是近场动力学理论下求解能量释放率的主要方法.基于Griffiths 能量释放率定义,Yu 和 Li (2020) 理论分析了近场动力学有限尺寸裂纹的能量释放率,包括二维中心裂纹、单边裂纹和弯折裂纹以及三维扁平型裂纹,并给出了不同裂纹形式的临界伸长率修正表达式.Zhang H 和 Qiao (2020b) 提出了近场动力学的有限裂纹伸长技术,计算单位长度裂纹扩展前后系统总应变能的变化值,数值求解了固定力或位移载荷作用下裂纹尖端的能量释放率.同一时期,Zhang H 和 Qiao (2020c) 构建了近场动力学理论框架下的虚拟裂纹闭合技术 (见图2),利用虚拟键能量密度积分计算裂纹闭合能量,采用裂纹尖端位移场分解的方式分析混合型裂纹,求解了I 型、II 型以及混合型裂纹的能量释放率.此外,弹性材料的能量释放率可利用近场动力学J积分求解.

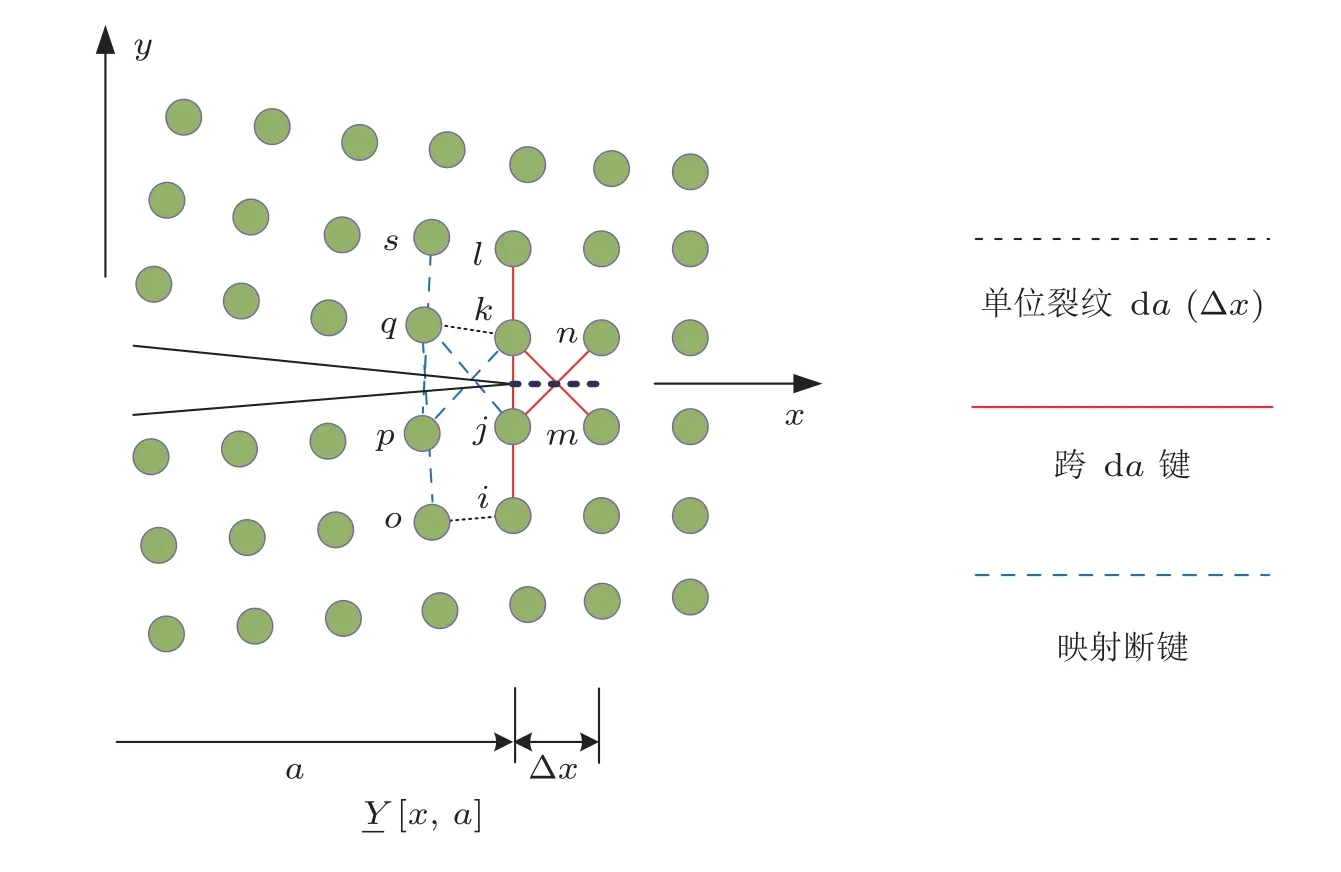
图2 近场动力学虚拟裂纹闭合技术 (Zhang H &Qiao 2020c).

Silling 和 Lehoucq (2010) 采用能量守恒定律首次推导了J 积分的近场动力学等效方程,并初步给出了该方程的求解形式.Hu W K 等 (2012a) 系统地提出了非局部J 积分的键基近场动力学理论模型和数值算法,研究了边界条件、表面效应以及积分路径对J 积分结果的影响,并对比传统有限元数值结果,验证了模型的有效性.如图3所示,不同与经典断裂力学的线积分形式,近场动力学内力的非局部积分区间为包裹积分路径的双层积分域.此后,Stenstrom 和 Eriksson(2019,2021) 给出了近场动力学J 积分的位移求解形式,避免了原模型的内力积分运算,提高了近场动力学J 积分的适用性和效率.

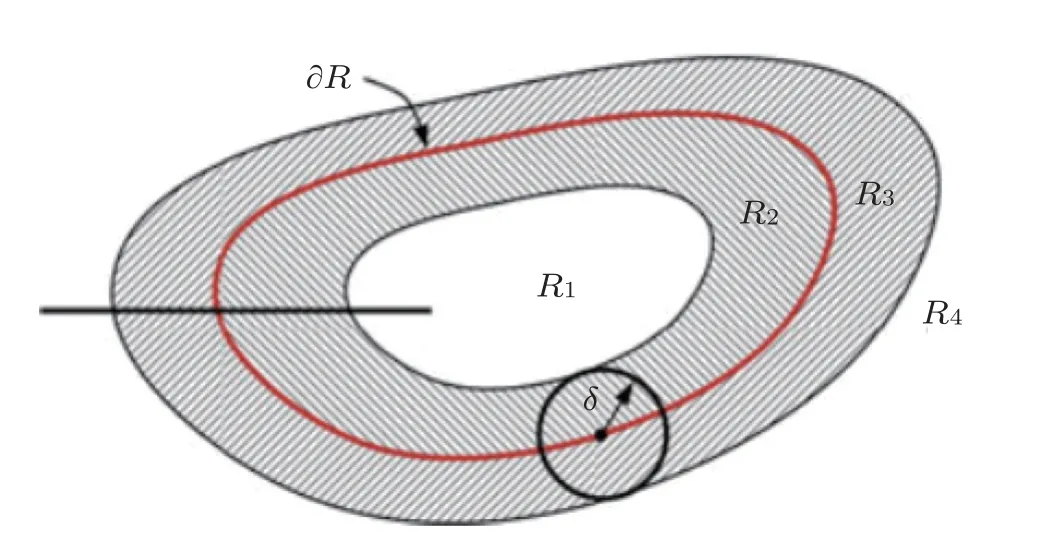
图3 近场动力学J 积分 (Hu W K et al.2012a).

利用近场动力学J 积分可进一步求解裂纹尖端应力强度因子.Jung 和 Seok (2017) 采用位移场分解方法分析混合型断裂,通过近场动力学J 积分计算裂纹尖端应力强度因子,并以此建立了混合型裂纹的近场动力学疲劳模型.Panchadhara 和 Gordon (2016) 利用近场动力学力矢量密度近似代替非局部应力张量,简化计算了传统断裂力学J 积分方程,分析了裂纹的I 型和II 型动态应力强度因子.另外,交互能量积分为J 积分方程中混合型应力强度因子的重要提取方法,Imachi 等 (2018) 采用最小二乘方法求解积分路径的位移导数,建立了常规状态近场动力学的交互积分方程,并分析了载荷作用下混合型裂纹的应力强度因子.此后,他们进一步求解了动态裂纹的应力强度因子,分析了裂纹的萌生、扩展和止裂等断裂行为 (Imachi et al.2019,2020).Dai等 (2021) 利用近场动力学微分算子实现了交互积分方程,求解了板壳结构在面内载荷作用下的应力强度因子.此外,Hattori 等 (2018) 与Zhu 和 Oterkus (2020) 采用位移外推法的近场动力学数值模型,分析了裂纹在准静态和动态载荷下的应力强度因子.

近场动力学理论的优势在于其消除了裂纹尖端的奇异性,不再需要基于断裂力学参数的断裂准则,其可自然模拟宏观上裂纹的萌生和扩展.因此能量释放率、应力强度因子和J 积分等断裂力学参数在近场动力学框架下的求解必要性受到质疑.尤其对于裂纹尖端的应力强度因子,其在近场动力学模型中缺乏具体的物理定义,往往通过近场动力学J 积分进一步求解得到.然而,近场动力学理论在量化分析复杂断裂问题,如混合型裂纹、界面裂纹等仍面临挑战.能量释放率等断裂参数可以表征出复杂裂纹尖端的宏观变形状态,也为同时发挥近场动力学和传统断裂力学的优势提供了可能.

4.2 混合型裂纹

断裂力学中裂纹类型包括: 张开型裂纹 (I 型)、滑开型裂纹 (II 型)、撕开型裂纹 (III 型) 以及混合型裂纹.经典的近场动力学临界伸长率和临界能量密度断键准则主要适用于I 型裂纹,在处理II 型、III 型以及混合型裂纹断裂问题时面临着挑战.一方面,对于均质各向同性材料,混合型载荷作用下裂纹倾向于弯折扩展,以保证混合型裂纹模式转换为能量消耗最低的I 型.经典临界伸长率或临界能量密度断键准则能够分析此类裂纹扩展问题,可以预测裂纹的扩展路径(Caimmi et al.2016,Madenci et al.2016,Dipasquale et al.2017),但在精确预测起裂临界载荷时遇到困难 (Zhang H et al.2021).另一方面,对于沿界面扩展的混合型裂纹,裂纹通常保持为混合型模式.然而经典断键准则没有充分考虑II 型和III 型断裂参数,在分析此类问题时会遇到裂纹面不完全断裂、裂纹临界载荷不准确等问题 (Ren et al.2016,Zhang Y &Qiao 2019a).

为更准确分析混合型断裂问题,Oterkus 和 Madenci (2012,2015) 建立了层间板界面混合型裂纹的近场动力学模型,提出了层合界面连接键的临界伸长率和临界剪切角断键准则,研究了复合材料界面脱层破坏以及反平面剪切和扭转变形引起的III 型断裂问题.对于同样的层间破坏问题,Hu Y L 等(2015) 将层间键能量密度分解为I 型、II 型和III 型断裂模式对应部分,并利用断裂力学混合型断裂准则,预测界面裂纹的萌生和扩展行为.Zhang Y 和 Qiao (2019a) 提出了II型断裂问题的临界偏转角断键准则,定义剪切变形下近场动力学键偏转角的求解方式,并推导得到临界偏转角与材料II 型临界能量释放率的等效关系,分析了剪切载荷作用下II 型裂纹断裂问题.Wang Y T 等(2018)、Yu H T 等(2020) 以及Madenci 等(2021) 分别利用键旋转角概念建立了广义键基近场动力学模型,避免了键基模型在材料参数泊松比上的限制,同时对应与键的伸长和旋转变形分别建立了临界失效准则,分析了二维和三维结构在拉伸、剪切、弯曲和扭转等复杂载荷共同作用下的裂纹扩展问题.近期,Zhang H 等 (2021) 提出了各向同性材料以及界面中混合型裂纹的近场动力学断键准则,推导了角度相关的临界伸长率和临界能量密度表达形式.如图4所示,分类定义混合型裂纹尖端近场动力学键,位移分解得到裂纹尖端I 型和II 型断裂模式对应的键变形状态,并引入Benzeggagh-Kenane (B-K) 或幂函数混合型断裂准则,建立了近场动力学混合型断键准则,分析了混合型裂纹的萌生、扩展和路径选择等断裂行为.此外,类比与经典断裂力学理论,研究者们利用近场动力学J 积分等方法求解了混合型裂纹的I 型和II 型应力强度因子,并分析了裂纹尖端的变形以及模态混合状态 (Jung &Seok 2017,Imachi et al.2018,Dai et al.2021).

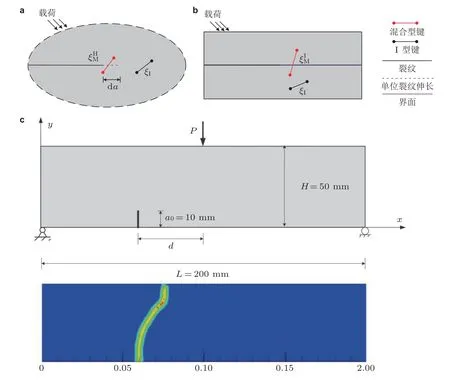
图4 混合型裂纹的近场动力学模型 (Zhang H et al.2021).(a) 各向同性材料,(b) 材料界面,(c) 应用展示.

近场动力学模型在分析混合型裂纹断裂问题时遇到挑战.一方面是因为不同裂纹类型对应键变形之间的混合,难以分解.不同方向上近场动力学键与裂纹面相对角度不同,其键变形中与I 型和II 型裂纹相关的权重也不相同.另一方面,经典近场动力学模型不能显式表征出键变形的剪切量,在分析II 型裂纹问题时遇到瓶颈 (Zhang Y &Qiao 2019a).广义键基近场动力学模型(Madenci 等 2021) 虽然同时定义了键的伸长和旋转变形,但该伸长和旋转变形并不能分别对应于I 型和II 型裂纹模式,其键变形混合作用依然存在.利用位移场分解的方法可得到裂纹尖端I型和II 型对应的键变形状态,但角度相关的近场动力学键失效准则需预知混合型裂纹的扩展方向 (Zhang H 等 2021).

4.3 弹塑性断裂

对于常用工程材料,裂纹尖端附近通常存在塑性区.针对材料的塑性变形响应,研究者们相继提出了弹塑性材料的近场动力学模型,分析了载荷作用下弹塑性结构的变形状态 (Mitchell 2011,Rahaman et al.2017,Javili et al.2021,Mousavi et al.2021).对于弹塑性材料的断裂问题,Madenci 和 Oterkus (2016) 系统性地建立了弹塑性材料的常规态近场动力学模型.模型引入von-Mises 屈服准则和各向同性强化模型,利用近场动力学等效应力和等效塑性伸长率构建了非局部塑性屈服面,分析了裂纹尖端的等效塑性伸长率和等效应力;同时考虑涉及弹塑性变形的临界能量密度断键准则,并利用临界断裂参数与非局部J 积分,研究了弹塑性材料的裂纹萌生和扩展以及塑性区演变 (见图5).为进一步分析裂纹尖端塑性区,Zhou 等 (2018) 研究了单轴拉伸载荷下不同倾斜角度裂纹尖端的塑性区大小和形状,采用SSY 小范围屈服条件和Mohr-Coulomb 屈服准则建立了近场动力学弹塑性模型,得到了与理论解相近的塑性区形状.Asgari 和 Kouchakzadeh (2019) 定义了弹塑性材料的近场动力学von-Mises 等效塑性应力和等效塑性应变,分析了中心裂纹尖端的塑性区变形状态,并与有限元结果比较,验证了塑性应力和应变定义的准确性.此外,Liu Z M 等 (2020) 与 Zhou 等 (2021) 分别利用非线性强化条件以及Drucker-Prager 屈服准则拓展了常规态近场动力学塑性模型,并分析了相应塑性材料的裂纹尖端变形情况.

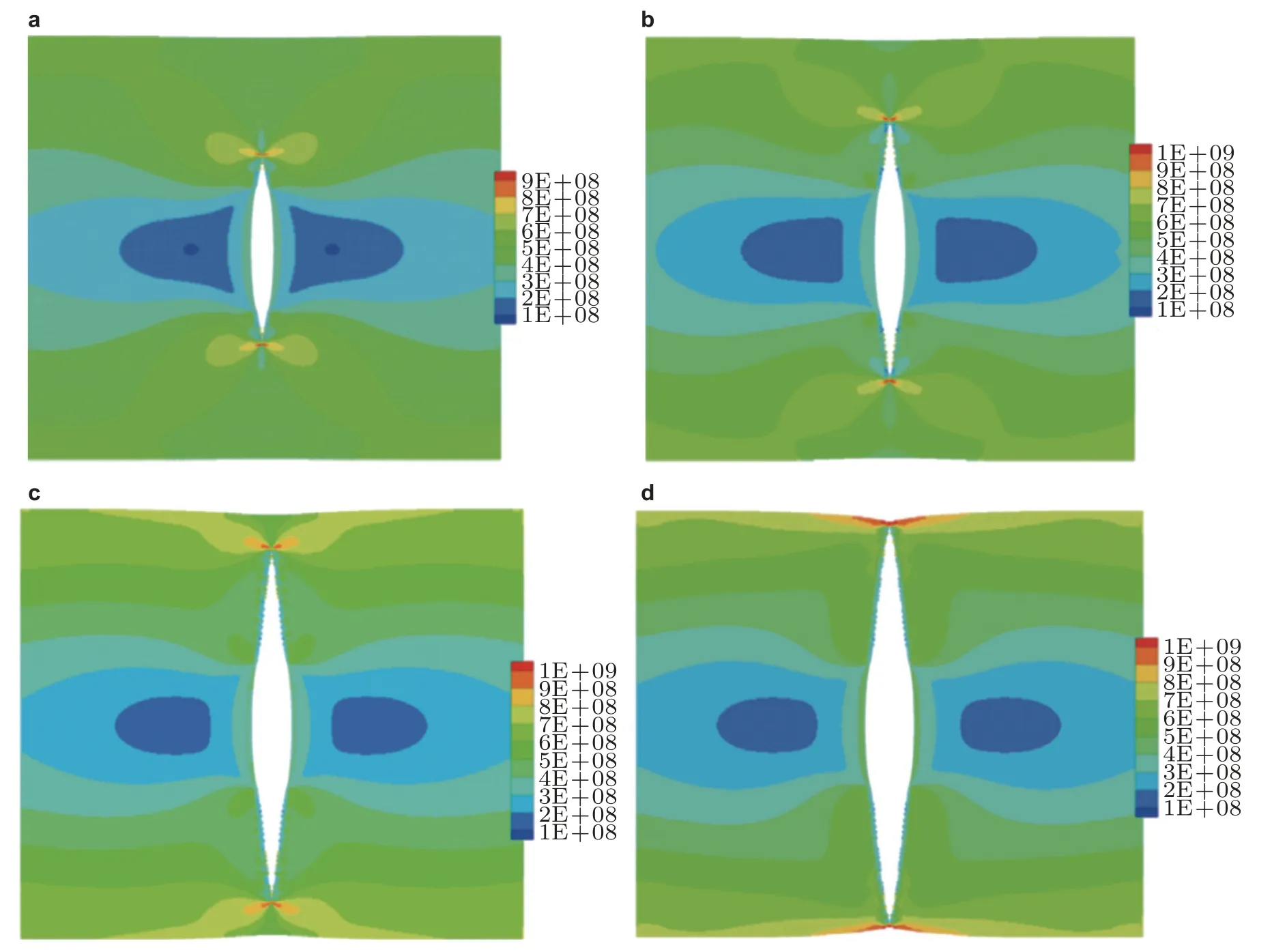
图5 位移载荷下弹塑性材料断裂中的等效应力分布 (Madenci &Oterkus 2016).(a) u=0.002 5 m,(b) u=0.003 m;(c) u=0.003 5 m,(d) u=0.004 m.

总的来说,现有关于弹塑性材料的近场动力学研究主要集中于非局部本构模型的构建,关于近场动力学弹塑性键失效准则,以及断裂量化分析的研究仍然较少.其中由于键伸长与键内力的非线性和历史相关性,经典基于临界伸长率的断键准则已不再适用于弹塑性材料,临界能量密度断键准则被研究者们广泛采用 (Madenci &Oterkus 2016).同时关于弹塑性断裂的研究主要为定性的裂纹扩展云图分析,对于如临界载荷、力-位移曲线、能量变化、裂纹速度等量化参数的分析仍然缺乏.

4.4 黏聚力模型

黏聚力模型可以处理裂纹尖端由塑性或微裂纹引起的内力变形非线性关系,是界面脱粘、准脆性断裂以及裂纹萌生等问题的重要分析手段.

Yang 等 (2018) 建立了键基近场动力学的离散黏聚力模型,如图6所示,采用非线性拉伸软化曲线表征键内力与键伸长的关系,同时考虑了单轴拉伸强度、弹性模型和断裂韧度材料参数,量化研究了混凝土I 型裂纹的准脆性断裂问题.之后,在此基础上理论推导了非局部黏聚力模型的伸长率极限等参数,引入近场动力学与有限元的耦合模型,并与传统黏聚力模型结果比较,验证了模型的有效性 (Yang et al.2020).为分析准脆性材料的剪切主导型断裂问题,Yang 等(2021) 提出了混合型断裂问题的非局部黏聚力模型,分解键能量密度为体积和剪切变形的部分,给出了关于键伸长率和体积膨胀能量的混合型失效准则,并利用隐式算法分析了拉伸软化突跳等物理非线性现象.另外,Rossi 等 (2019) 在键基近场动力学模型的基础上,提出了双线性的本构力函数,研究了准脆性材料的损伤演化过程.Tong 等 (2020a,2020b) 提出近场动力学键损伤概念,利用衰减函数表征峰值力之后的键残余作用力,并引入自适应有限元耦合模型,建立了粘性材料的近场动力学渐进损伤模型,并分析了混凝土结构的渐进破坏过程.Gui 等 (2021)建立了复合材料层压板的近场动力学黏聚力模型,采用双线性粘性定律和Benzeggagh-Kenane (B-K)断裂准则,分析了混合型载荷作用下的界面脱粘问题.

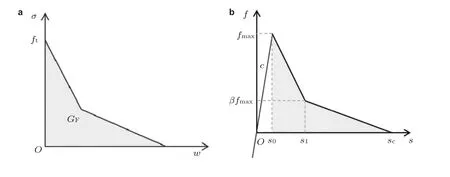
图6 传统断裂力学和近场动力学粘聚力模型.(a) 传统断裂力学粘聚力模型,(b) 近场动力学粘聚力模型 (Yang et al.2018).

4.5 动态断裂问题

近场动力学理论提出以来,被广泛地应用于动态断裂问题.Diehl 等 (2019) 与 Isiet 等(2021) 分别综述性介绍了基准动态试验以及冲击载荷下材料动态破坏的近场动力学研究.代表性的,Silling (2003) 首次利用近场动力学模型分析了Kalthoff-Winkler 动态断裂试验;Ha 和Bobaru (2010,2011) 研究了裂纹的动态扩展和分叉 (如图7);Agwai 和 Guven (2011) 利用键基近场动力学模拟了动态裂纹扩展问题,并对比了扩展有限元以及黏聚力模型结果.之后,近场动力学模型被应用到不同材料和结构的动态断裂分析,包括各向异性材料 (Hu W K et al.2012b,Ghajari et al.2014),功能梯度材料 (Cheng et al.2015,Ozdemir et al.2020),混凝土 (Wu P et al.2021,Wu &Huang 2022) 和岩石 (Zhou &Wang 2016,Zhou et al.2016) 等.依据求解方式,近场动力学的动态断裂分析研究主要可分为两类.其中主要的一类,利用临界伸长率或临界能量密度近场动力学断键准则,模拟动态载荷作用下裂纹萌生、扩展以及分叉等现象,分析裂纹速度、临界载荷以及能量分布等断裂参数.另一类,参照经典断裂力学理论,研究者们利用近场动力学J积分等方法求解了裂纹尖端的断裂力学参数,并研究动载荷下静止裂纹和扩展裂纹的动态应力强度因子 (Panchadhara &Gordon 2016,Hattori et al.2018,Imachi et al.2018).

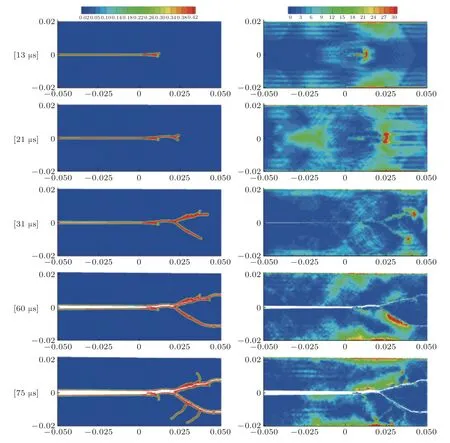
图7 应力载荷σ=23 MPa 下不同时刻裂纹动态扩展和分叉以及应变能密度分布 (Ha &Bobaru 2011).

严格来说,动态断裂是一个涉及惯性效应和材料非线性的问题,材料的动态断裂韧度等参数往往与加载速率、裂纹的扩展速度等因素有关.考虑动态断裂问题的惯性效应,研究者们建立了变形速率敏感的近场动力学模型.Silling 和 Askari (2005) 首次提出了随时间变化的实时临界伸长率概念.Kilic (2008) 定义了近场动力学键伸长变化率的形式,并建立了伸长变化率敏感的微弹性本构力模型.在伸长变化率定义的基础上,Sun 和 Huang (2016) 分析了层合复合材料的冲击破坏问题;Chu 等 (2020) 与 Liu Y X 等 (2022) 采用Johnson-Holmquist (JH-2) 本构建立了考虑材料损伤、变形率和变形历史的键基近场动力学模型,并分析了陶瓷材料的动态断裂行为.此外,研究者们分别利用Holmquist-Johnson-Cook (HJC) 混凝土模型、ZWT 粘弹性模型以及Johnson-Cook (JC) 弹塑性模型,建立了适用于混凝土、PMMA 和复合材料的变形速率敏感的近场动力学模型,并利用它们分析了材料的动态断裂行为 (Wu L W et al.2020,2021;Zhan et al.2021).

此外,为提高动态断裂问题的近场动力学计算效率,研究者们提出了不同类型的离散化和耦合模型,包括: 自适应网格 (Dipasquale et al.2014,Shojaei et al.2018)、有限元近场动力学耦合模型 (Macek &Silling 2007,Han et al.2016,Ni et al.2018) 以及物质点近场动力学耦合模型(Zeng et al.2022) 等.

4.6 材料界面断裂

材料界面断裂是一个涉及裂纹模态混合、扩展路径选择和裂纹面接触的复杂问题.为表征材料界面,Seleson 等 (2013) 与 Alali 和 Gunzburger (2015) 分别建立了近场动力学非局部界面模型,理论分析了材料界面的收敛性和非局部扩散问题.针对材料界面的断裂问题,Wang F 等(2014) 与 Zhang H 和 Qiao (2018c) 利用临界伸长率的近场动力学断键准则,分析了载荷作用下的材料界面脱粘问题.Zhang Y 和 Qiao (2019b) 提出了近场动力学界面接触力模型,并采用临界能量密度断键准则分析了纤维拔出问题,模拟了界面裂纹起裂、沿界面扩展以及摩擦接触的破坏过程.近期,Behera 等 (2021) 建立了粘弹性材料的非常规态近场动力学模型,考虑了有厚度的胶接界面层,并利用临界伸长率模型分析了单搭接和双搭接胶接节点的界面失效和破坏形式.此后,该模型被拓展至常规态近场动力学模型 (Anh et al.2022).对于界面裂纹路径选择问题,Qin 等 (2021) 利用键基近场动力学模型研究了各向异性岩石界面层的水利压裂问题,模拟了岩石裂纹的横跨界面、弯折、分叉和止裂等断裂行为.Zhang H 等 (2022) 利用近场动力学模型分析了双弹性材料界面的断裂问题.如图8所示,推导了常规态近场动力学材料界面的力传递形式,采用近场动力学虚拟裂纹闭合技术求解了界面裂纹的能量释放率和模态混合度;分类定义跨界面键与母材内部键,提出模态混合度相关的界面键失效准则,并建立了界面裂纹路径选择的键失效竞争模型,分析了界面裂纹沿界面或折出界面的路径竞争问题.然而该模型仅可用于分析弹性材料界面,对于具体的工程结构问题,如钢筋混凝土界面、金属陶瓷界面和热障涂层界面等,涉及材料弹塑性变形响应和热耦合效应,仍需进一步的研究.

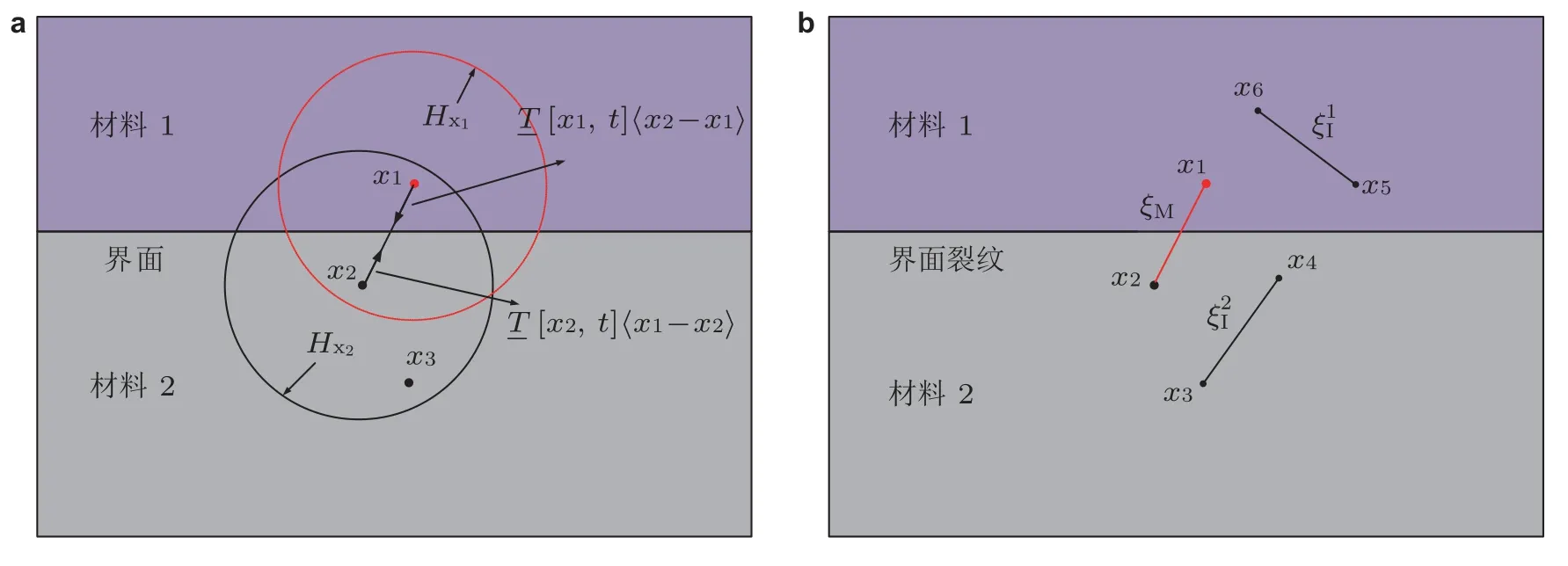
图8 双弹性材料界面的近场动力学模型 (Zhang H et al.2022).(a) 材料界面非局部力传递,(b) 近场动力学跨界面键与母材内部键.

4.7 疲劳裂纹扩展

疲劳裂纹扩展规律是断裂力学研究的重要领域,对工程结构设计具有重要指导作用.Oterkus 等 (2010) 首次给出了循环载荷下键基近场动力学模型的疲劳定义,分析了材料裂纹扩展阶段的疲劳寿命.此后,Silling 和 Askari (2014) 系统性地建立了近场动力学的疲劳模型,为疲劳裂纹的分析奠定了基础.如图9所示,在该模型中,定义了循环载荷下近场动力学键的循环应变范围,并建立了不同疲劳断裂阶段的键寿命模型.在疲劳裂纹萌生阶段,开展不同循环应变的疲劳数值试验,对比S-N 疲劳实验曲线,提取萌生阶段近场动力学疲劳参数;在裂纹扩展阶段,类比疲劳裂纹扩展率Pairs 准则,建立近场动力学疲劳裂纹扩展模型.利用该近场动力学疲劳模型,Jung 和 Seok (2016) 与 Zhu 等 (2021) 分别研究了循环载荷下层合非均质材料与多晶材料的疲劳断裂问题;Hong 等 (2021) 与 Ma 等 (2022) 分析了角焊缝接头和铁轨中的疲劳裂纹萌生和扩展.在Silling 的疲劳模型基础上,Zhang G F 等 (2016) 利用临界损伤因子追踪裂纹路径,提高了计算效率和稳定性,预测了均质材料以及两相复合材料的疲劳裂纹演化过程.Jung 和 Seok(2017) 引入了修正的Paris 准则以及近场动力学J 积分,求解了I-II 混合型裂纹的疲劳断裂.Liu B C 等 (2020) 建立了近场动力学疲劳损伤累积模型,研究了相界面对TC18 钛合金疲劳裂纹偏转的影响.此外,Hu 和 Madenci (2017) 利用S-N 疲劳曲线修正材料的临界能量释放率,分析了带圆孔复合材料层合板的疲劳破坏.Nguyen 等 (2021) 提出了一种基于键能量密度的近场动力学疲劳模型,分析了疲劳载荷下混合型裂纹的萌生和扩展.Bang 等 (2021) 分别利用数值和解析方法以及疲劳试验数据求解了近场动力学疲劳模型参数.对于低周疲劳问题,Li 等 (2022) 提出了弹塑性材料的非常规态近场动力学疲劳模型,采用了关联流动法则与混合硬化模型,研究了低循环载荷下的滞后回线以及疲劳断裂.

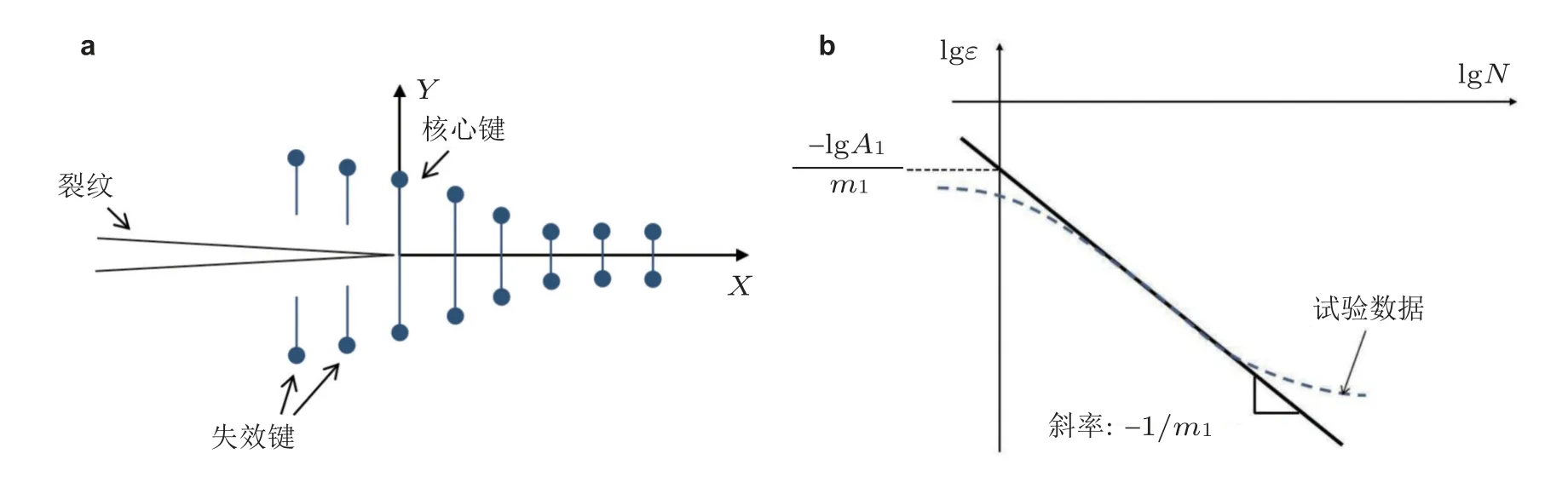
图9 近场动力学疲劳模型 (Silling &Askari 2014).(a) 裂纹尖端近场动力学键,(b) 近场动力学疲劳模型参数校正.

总的来说,近场动力学在断裂力学多个领域都取得了不错的进展,也面临了一些挑战.同时,涉及多尺度和多物理场耦合作用的断裂问题为力学界的前沿课题,近场动力学在多尺度和多物理场耦合问题上也取得了一些研究成果.乔丕忠等 (2017) 和顾鑫等 (2019) 综述性介绍了近场动力学在多尺度和多物理场耦合问题的研究进展.

5 结 论

近场动力学采用非局部积分计算节点内力,避免了非连续区局部空间导数;利用了统一数学框架描述空间连续与非连续,避免了非连续条件处理,因此可自然模拟固体结构的断裂损伤问题.本文系统总结了近场动力学的弹性本构力模型和键失效模型,详细介绍了近场动力学在断裂参数求解、混合型裂纹、弹塑性断裂、黏聚力模型、动态断裂、材料界面断裂和疲劳裂纹扩展方面的研究进展.

发展至今,近场动力学在断裂力学问题上充分展现了其优势.随着研究的深入,近场动力学研究从最初的线弹性、各向同性材料、I 型裂纹的定性分析逐渐拓展到塑性、各向异性材料、混合型裂纹的定量分析,此外如界面断裂、疲劳裂纹扩展等经典断裂问题的近场动力学研究近年来受到更多关注.同时,仍有诸多断裂问题需要进一步研究,如: 混合型裂纹的量化分析、弹塑性材料的失效模型、三维裂纹的表征和模拟、夹杂结构的断裂分析以及裂纹尖端多尺度微观表征等.

致 谢国家自然科学基金 (12172192,11972224,12102226)、中国博士后科学基金 (2021M691798)资助项目.