基于扰动观测器补偿的双惯量系统和三惯量系统的谐振抑制

何朕，成知宁，王宁远，孟范伟

(1.哈尔滨工业大学 航天学院，黑龙江 哈尔滨 150001；2.东北大学秦皇岛分校 控制工程学院，河北 秦皇岛 066004)

0 引 言

从工业制造到高端医疗器械，从新能源产业到航空航天，伺服系统广泛应用于各领域中[1-5,30]。但不可忽视的是，系统中由于传动轴的弹性连接所引发的谐振现象，极大影响了系统的精度，甚至使系统不稳定[27,29]。因此，对谐振抑制的研究是很有必要的。

通常情况下，实际系统由双惯量系统(2-inertia system)来描述。由此，目前大多的研究也主要集中在双惯量系统的谐振抑制，并提出了诸多有效的方法，例如PID控制[6-7]、自适应控制[8-9]、鲁棒控制[10,26]、滑模控制[11-14]等。文献[15]针对带有双编码器的柔性连接执行机构，构造了一种扰动观测器，实现了由于柔性连接使得系统呈现弱阻尼挠性所引发的谐振的抑制。文献[16]针对双惯量系统提出了PID-P的控制结构，并利用系数图法(coefficient diagram method，CDM)对控制器的参数进行选取，有效抑制了系统的机械谐振。文献[17]和文献[18]设计一种滑模观测器对电机加速度和负载速度进行估计并反馈到系统中进行补偿，解决了大惯量扫描镜伺服控制系统中柔性连接带来的机械谐振问题。此外，一些智能控制方法也被用于解决此类问题。神经网络控制[19-21]和模糊控制[22-23]凭借着其近似能力较好的学习效果，也在解决谐振抑制问题中发挥了不错的效果。

然而，针对于实际的物理系统来讲，一般系统中存在的谐振模态却不止一个，此时系统便成了一个三惯量系统(3-inertia system)。现在的工作一般都聚焦在双惯量系统上，文献[24]指出，基于CDM法对双惯量系统的陷波滤波设计不适用于三惯量系统，该文进而对三惯量系统的谐波抑制进行了特殊的复杂设计。文献[25]将三惯量系统近似为双惯量系统进行描述，并采用状态反馈结合PI控制实现了谐振抑制，但设计过程是依据双惯量模型进行的。结合目前已有的研究成果，人们将谐振抑制问题仍主要聚焦在双惯量系统上，且并未从一个统一的结构来对两类系统进行设计。

因此，相比于前人的工作，本文从等效名义对象角度入手，将双惯量和三惯量系统进行统一讨论，针对两类系统的电机侧位置控制提出一个新的控制结构，使得此类结构可以同时解决两类系统的谐振抑制问题。该结构由扰动观测器和控制器两部分构成，其中扰动观测器用于将实际系统等效成名义对象(刚体)；在此基础上，设计控制器以实现系统的谐振抑制和对输入信号的精确跟踪。具体来说，文中分别将三惯量系统中的齿轮转矩Tg和双惯量系统中的传动轴转矩Tc等视为电机侧的“扰动”。所设计的扰动观测器利用系统的控制输入(即电机输入转矩)和电机转速作为输入信号，经低通滤波器作用后，估计出系统的“扰动”，等效为名义对象。此外，本文基于双曲函数提出一种新的滑模趋近律，解决了传统滑模控制中存在的抖振现象，并通过仿真验证所提方法的有效性。

本文第1部分建立了系统的数学模型，对问题进行了陈述；第2部分给出基于扰动观测器补偿的控制策略；第3部分通过仿真对本文所提方法的有效性进行验证；第4部分对全文作出总结。

1 系统模型

根据典型传动系统的结构分别建立了双惯量系统和三惯量系统的数学模型，并结合所得到的数学模型对系统的动态特性进行分析。

一个典型传动系统主要由驱动电机、负载和传动装置(齿轮、传动轴等)组成，其大致结构如图1所示。在此结构中，电机通过齿轮和传动轴驱动负载，两者由于传动装置的阻尼系数和刚度系数发生耦合。电磁转矩和传动装置上的转矩共同作用于电机，以决定电机的输出转速；同时，传动装置上的转矩和负载转矩共同作用于负载，以决定负载角速度。在此情况下，当我们将齿轮的影响考虑在内时，此时的传动系统可以由一个三惯量系统来描述，如图2所示。

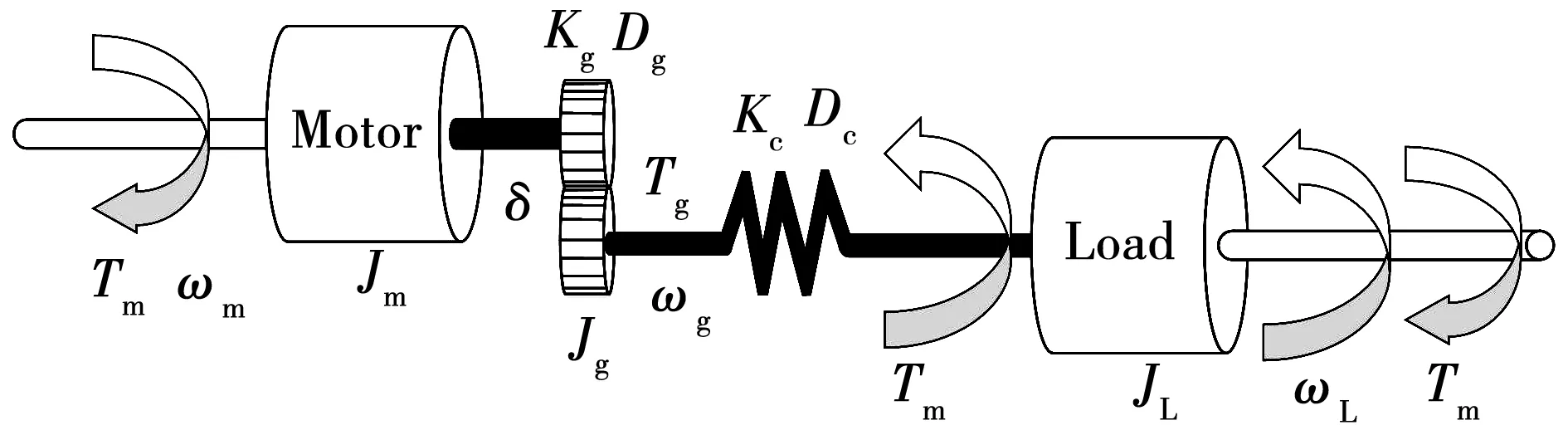
图1 传动系统结构图Fig.1 Structure of transmission systems

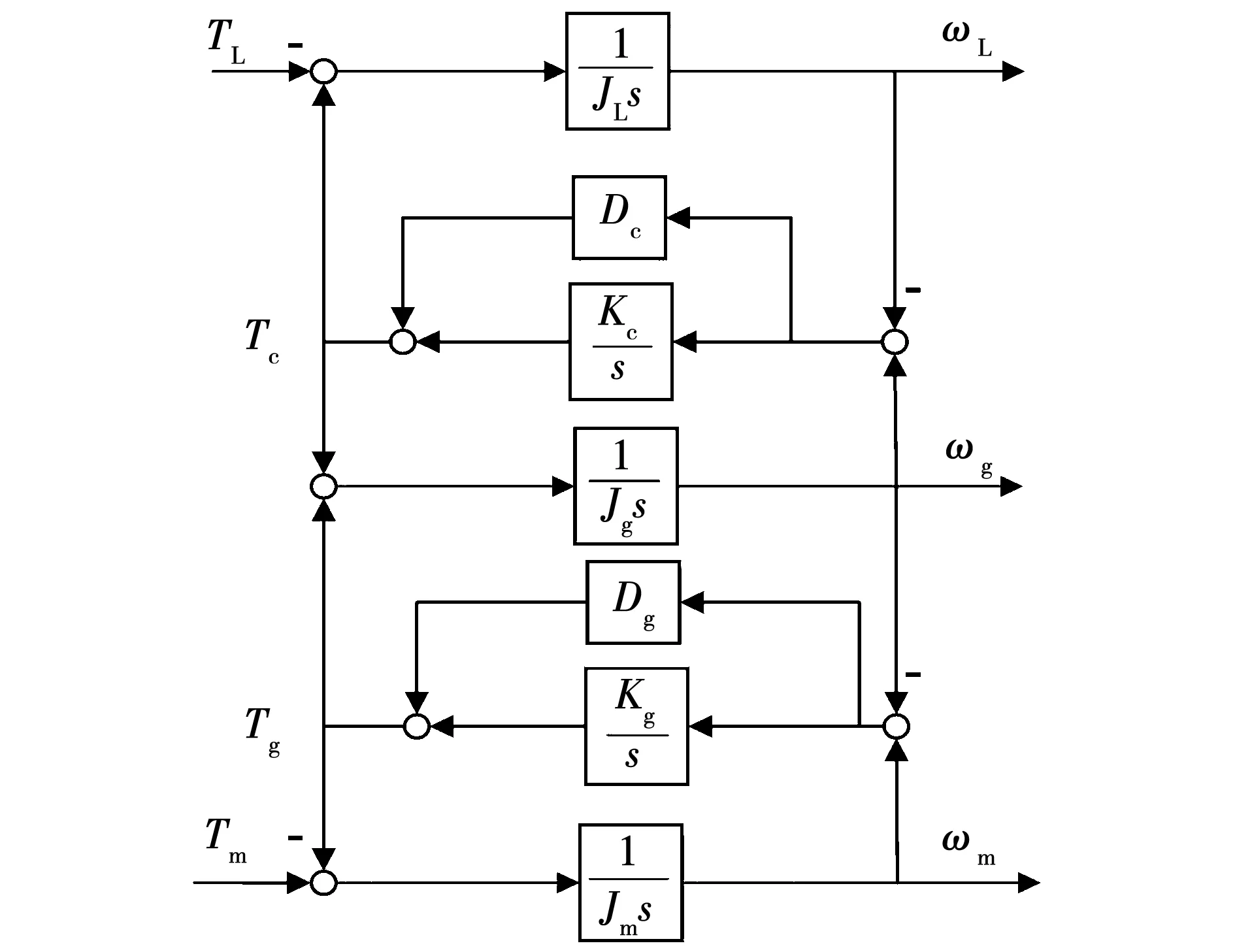
图2 三惯量系统结构图Fig.2 Block diagram of three-inertia system

根据图2，当忽略齿隙的影响，即δ=0时，此时三惯量系统的数学模型可以表述为：

(1)

(2)

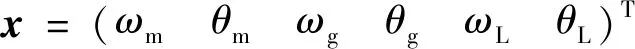
图3中实线给出了三惯量系统从Tm到θm的频率特性，各参数具体数值可见表1。从图中可以看到，此时系统中存在两个谐振峰(78、236 rad/s)分别对应由传动轴和齿轮所引起的谐振现象，且两频率较为接近容易同时被激发，使系统发生机械振荡。

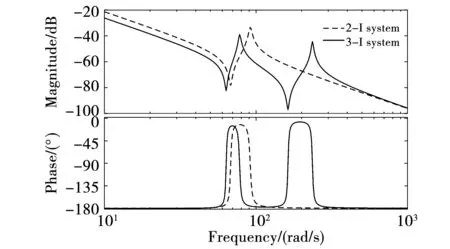
图3 两系统频率特性Fig.3 Frequency response characteristics(2-I system &3-I system)

表1 仿真模型的参数[24]Table 1 Parameters of simulation model[24]

事实上，当忽略掉齿隙影响时，考虑到齿轮的刚度系数Kg通常远大于传动轴的刚度系数Kc，此时三惯量系统可简化为双惯量系统，结构如图4所示。图4中，Jmg(=Jm+Jg)作为齿轮和电机的等效转动惯量。

整理后可得双惯量系统的数学模型为：

(3)

(4)

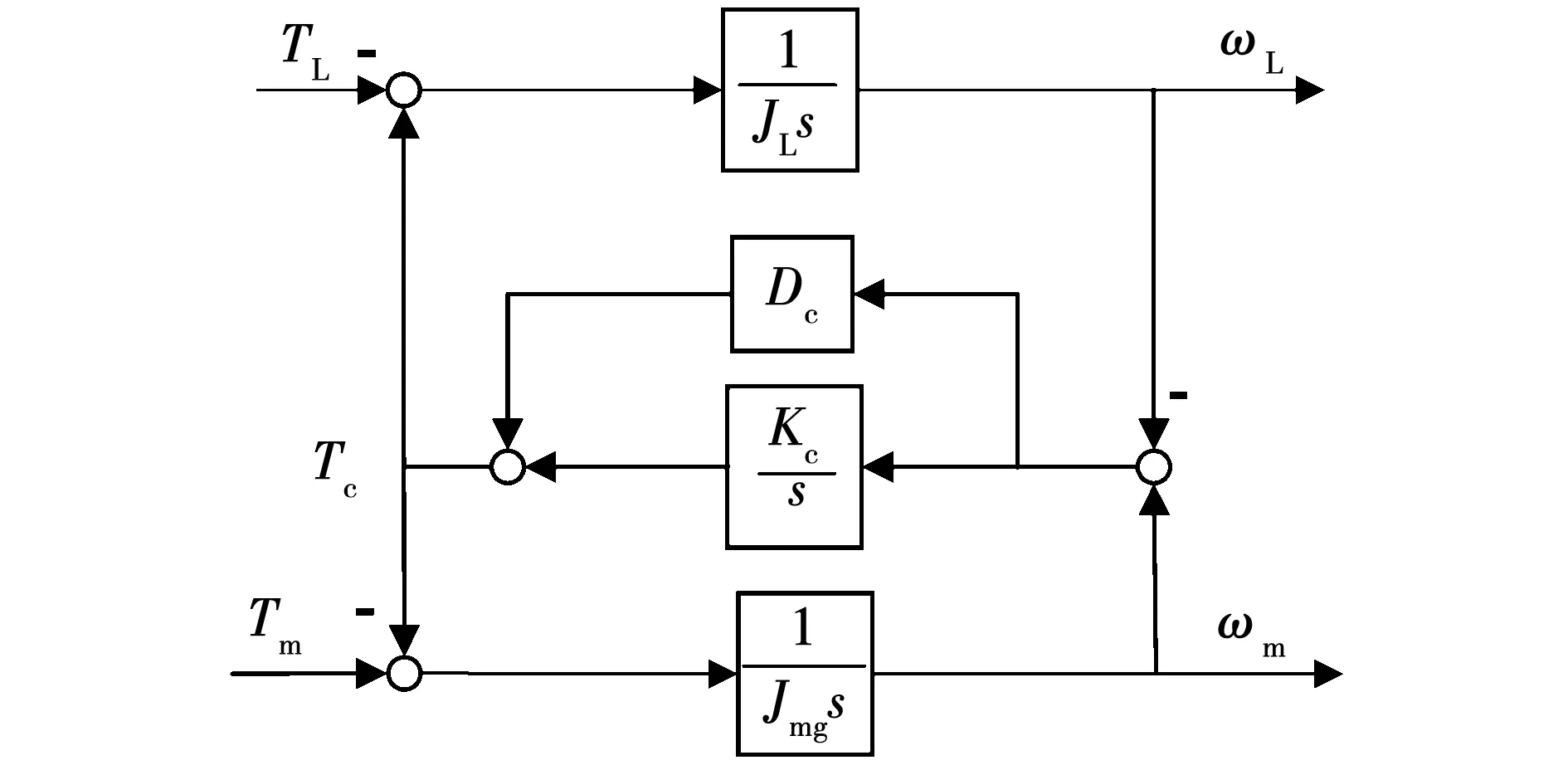
图4 双惯量系统结构图Fig.4 Block diagram of two-inertia system

同样地可以整理出对应双惯量系统中从电机输出转矩Tm到电机角度θm的开环传递函数为

(5)

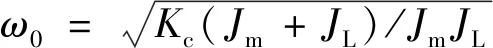
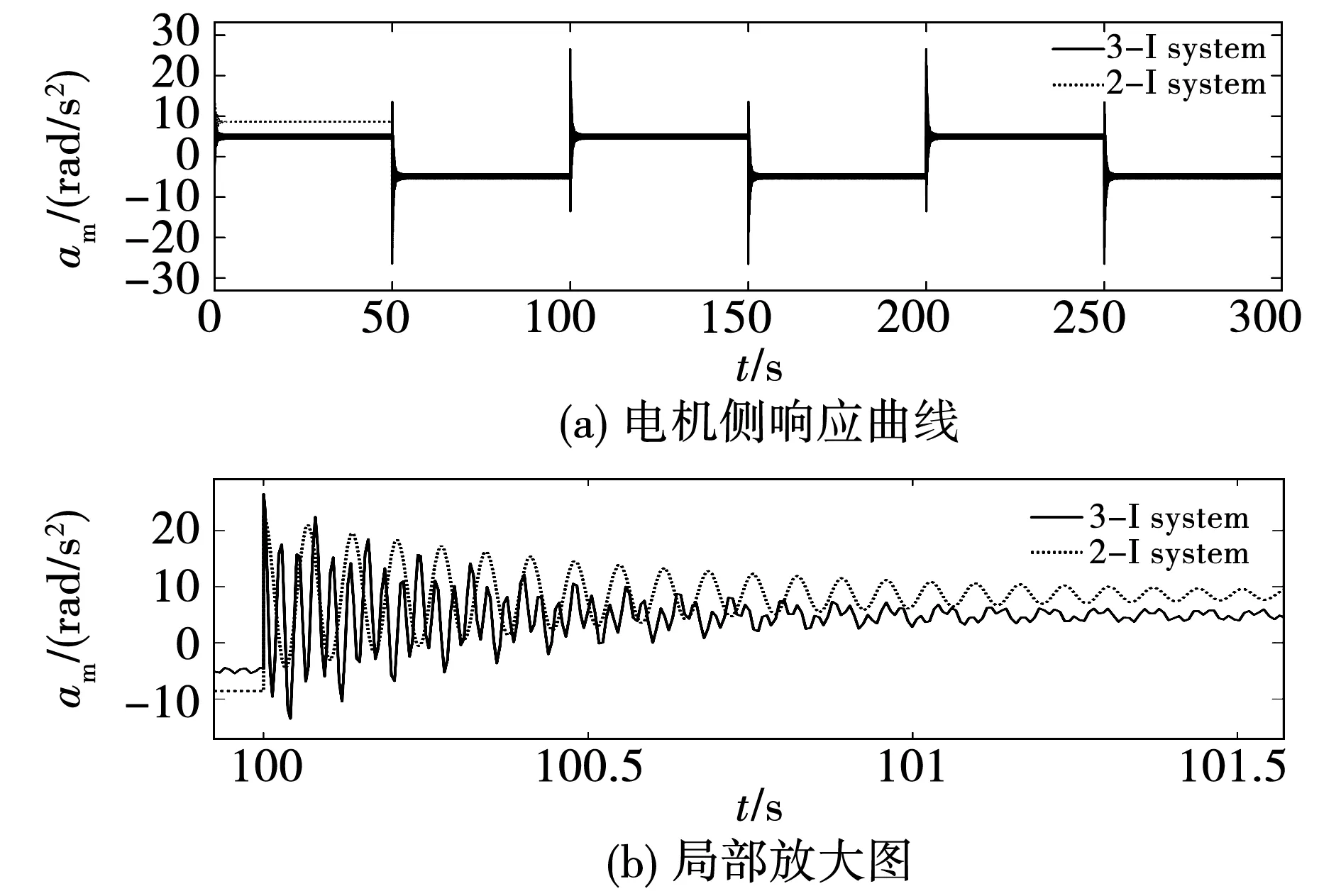
图5 两系统方波响应Fig.5 Response of square signal in two systems

从以上分析中可以得知，无论是对于三惯量系统还是双惯量系统而言，两者都是因为系统阻尼系数的值非常小，从而在幅值特性中表现出两个或一个谐振峰，前者分别先后对应着三惯量系统中柔性传动轴发生扭振时的谐振频率和齿轮的谐振频率，后者对应简化后的双惯量系统中柔性传动轴发生扭振时的谐振频率。

因此，本文的目标如下：1)设计扰动观测器进行补偿，将系统等效成名义对象；2)设计控制器使得系统电机侧位置准确跟踪给定输入信号。

2 基于扰动观测器的补偿策略

由式(1)～式(4)，假设负载转矩TL=0，两类系统的运动方程均可表述为

(6)

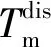
为了更好地抑制系统中的机械谐振，本部分的主要内容为设计基于扰动观测器的补偿环节将系统等效转化为名义对象，从而实现系统的谐振抑制。

2.1 扰动观测器设计

扰动观测器(disturbance observer,DOB)的原理是将作用在系统上的扰动信号视为另外一个动态系统的输出信号，通过对这一个子系统的状态进行估计以实现对扰动信号的补偿[26]。在这里，我们主要分别将双惯量系统中的Tc和三惯量系统中的Tg视作各自的电机侧扰动，然后考虑利用扰动观测器对此进行估计并补偿，从而将真实系统转化为名义对象来进行控制设计。图6给出了扰动观测器的原理结构图。

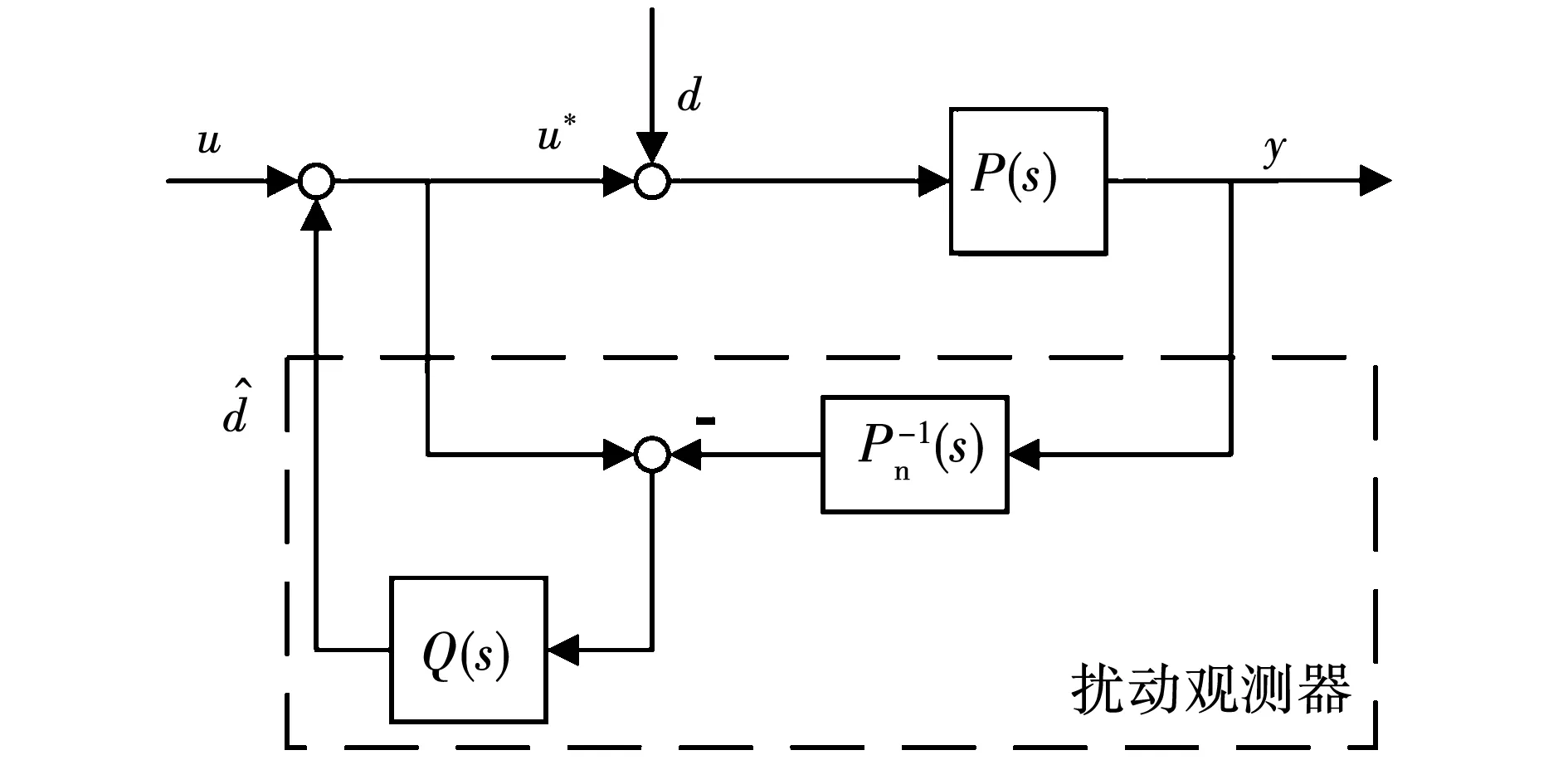
图6 扰动观测器原理图Fig.6 Structure of disturbance observer

从图6可得系统的输入输出关系式为

y=Guy(s)u+Gdy(s)d。

(7)

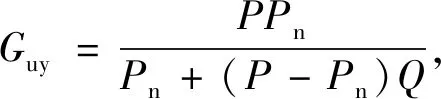
在低通滤波器Q(s)的频段内，Q(s)≈1，从而有Guy≈Pn,Gdy≈0。这就意味着当扰动信号的最大频率依然小于Q(s)的剪切频率时，扰动信号能够得到很好地抑制，并且真实系统表现为名义对象。显然，在具体的设计中，滤波器Q的选取决定了系统的鲁棒性和扰动抑制性能，考虑到系统的带宽要受到鲁棒稳定性的限制，所以Q(s)的频段设计要在扰动抑制和鲁棒稳定性之间取一个折中。

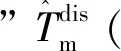
(8)

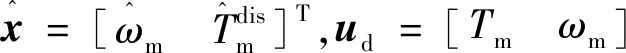
(9)

图7和图8分别给出了在不同g值下，两系统的开环频率特性曲线。对于双惯量系统来说，只存在一个谐振峰，随着g值不断增加，谐振峰值不断被压低。

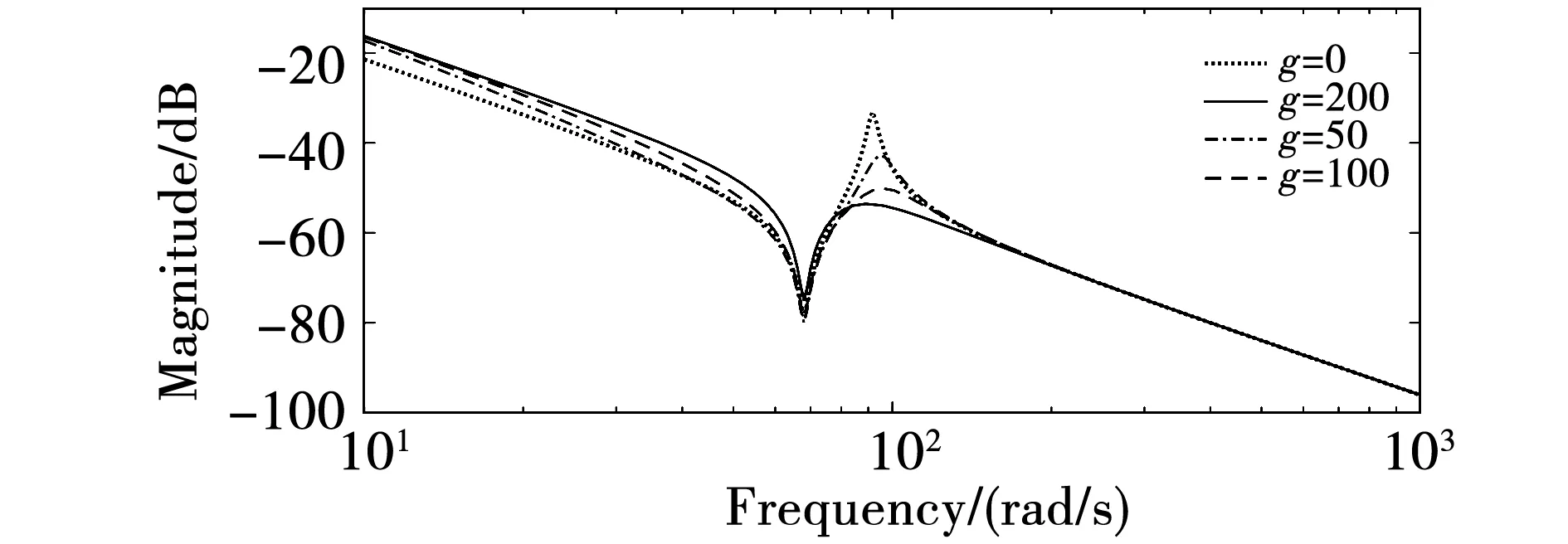
图7 扰动观测器下双惯量系统频率特性Fig.7 Frequency response of 2-I system with DOB

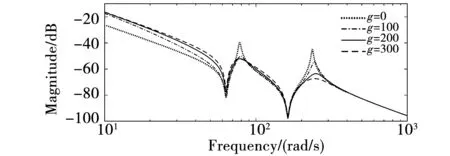
图8 扰动观测器下三惯量系统频率特性Fig.8 Frequency response of 3-I system with DOB

当g值为200 rad/s时，双惯量系统在92 rad/s处的谐振峰值衰减了20.6 dB。在三惯量系统中，78 rad/s和236 rad/s两处的谐振峰值随g值增加而得到衰减。当g值等于200 rad/s时，两处谐振峰值分别衰减了13 dB和23.1 dB。从图7和图8可以看出，只要设计合适的带宽，使过0的带宽ωc低于第一个凹陷频率，那么这两类系统的谐振模态都可得到抑制。

2.2 控制器设计

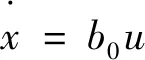
受双曲函数的启发，结合对快速收敛性的考虑，本文提出一种滑模趋近律

(10)

式中：s为滑模变量；k1,k2,a,b为正参数；tanh(as)=(eas-e-as)/(eas+e-as)为双曲正切函数；sinh(bs)=(ebs-e-bs)/2为双曲正弦函数。

当滑模变量s远离平衡点时，-k2|s|sinh(bs)的值远远大于-k1tanh(as)的值，从而滑模变量s受前者作用能够快速收敛。当滑模变量s在平衡点附近时，-k2|s|sinh(bs)的值近似为0。此时，滑模变量s的变化主要由-k1tanh(as)控制。此类双曲函数型趋近律的主要特点表现在当系统初始状态远离平衡点时，快速收敛性能够得到保证。同时，滑模变量s无限趋近于平衡点却不到达或者穿越。由此，传统滑模趋近律中由于sgn(·)函数引起的抖振现象能够得到很好地消除。

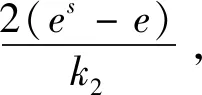
接下来，结合扰动观测器和所提出的趋近律设计滑模控制器。

此时，定义θm=x1,ωm=x2，系统的数学模型变为：

(11)

为了设计滑模控制器，定义系统的跟踪误差

(12)

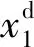
线性滑模面定义为

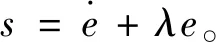
(13)

式中λ>0。对式(13)求导有

(14)

将式(11)、式(14)结合式(10)可得控制律为

(15)

式中：k1,k2均为需要调节的参数，且大于0。

此时，选取李雅普诺夫函数为

(16)

系统的稳定性显然得证。

由于这里的控制律uc是基于DOB作用后的纯积分模型设计的，因此最终的控制律为

(17)

3 仿真分析

扰动观测器的带宽g=200 rad/s；滑模控制器的参数选取为k1=k3=10,k2=5,λ=1.7,b=1/Jm,a=5,b=0.2；参考信号为一方波周期信号。为了确保参考输入轨迹平滑，利用二阶环节进行滤波，即

(18)

其中：xr(s)是给定的方波周期信号；xd(s)是系统输入信号；gf是滤波参数，这里取值为3。

图9和图10中的实线和虚线分别给出了引入扰动观测器前后，双惯量系统和三惯量系统电机侧加速度的响应情况。虽然滑模控制能够一定程度上处理机械谐振的不利影响，但在扰动观测器作用下，系统响应曲线中的振荡幅度明显降低。同时结合图5对比，结果表明，通过采用扰动观测器进行补偿，两类系统中电机侧加速度响应均更加平滑，而系统中由于柔性环节产生的机械谐振得到了很好的抑制。

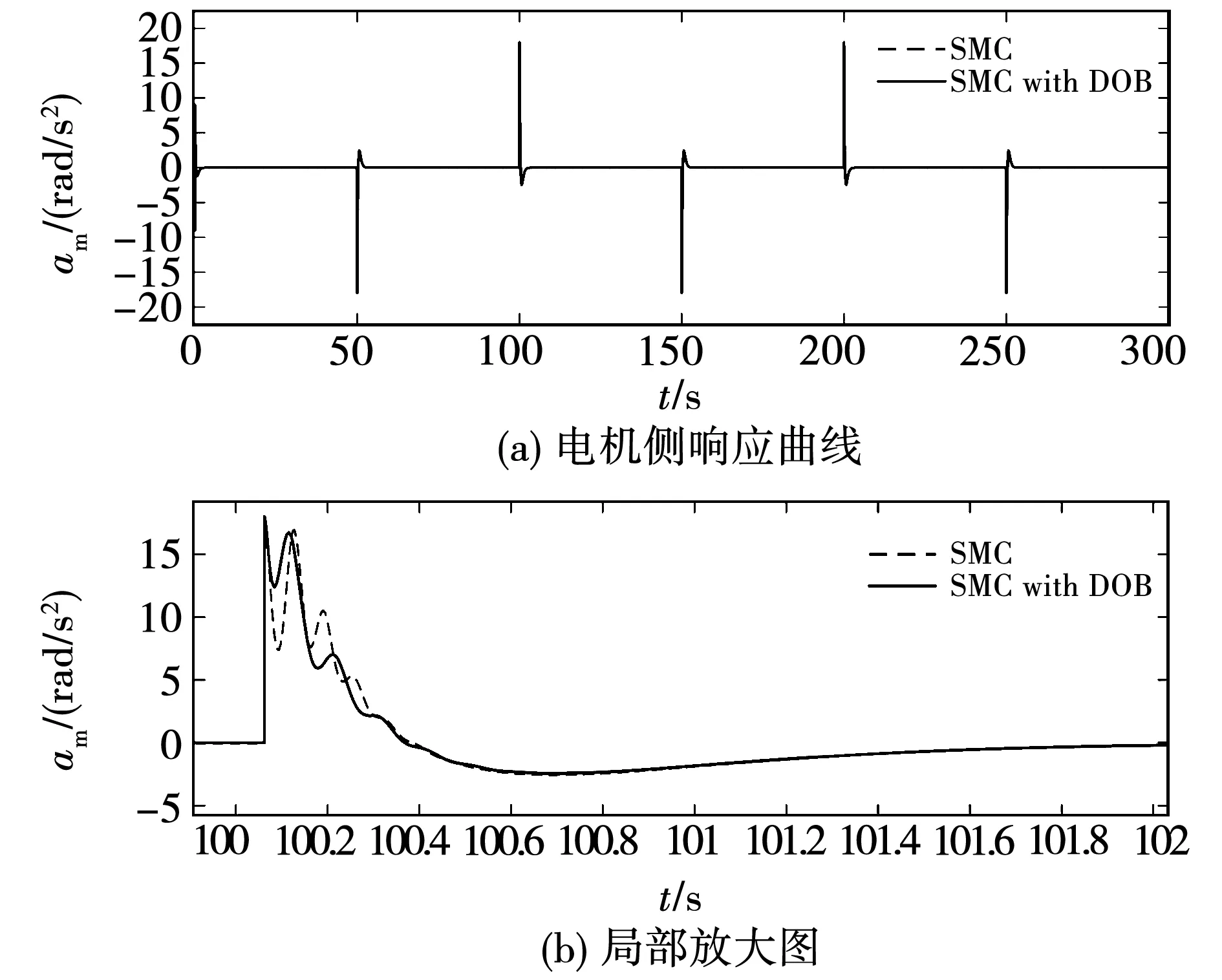
图9 双惯量系统谐振抑制效果Fig.9 Vibration suppression performance of 2-I system

图11～图14分别给出了在输入幅值为1 rad，周期为100 s的方波信号下，两系统各自的跟踪效果及误差。从图中可以看到，在本文提出的控制结构下，两系统均实现了对给定信号准确、快速、平滑地跟踪。与此同时，系统跟踪误差始终保持在±0.003 rad内，系统的动态特性以及稳态性能得到极大改善，这主要是因为所设计的扰动观测器对电机侧扰动实现了有效估计和补偿，此时系统表现为名义对象特性。

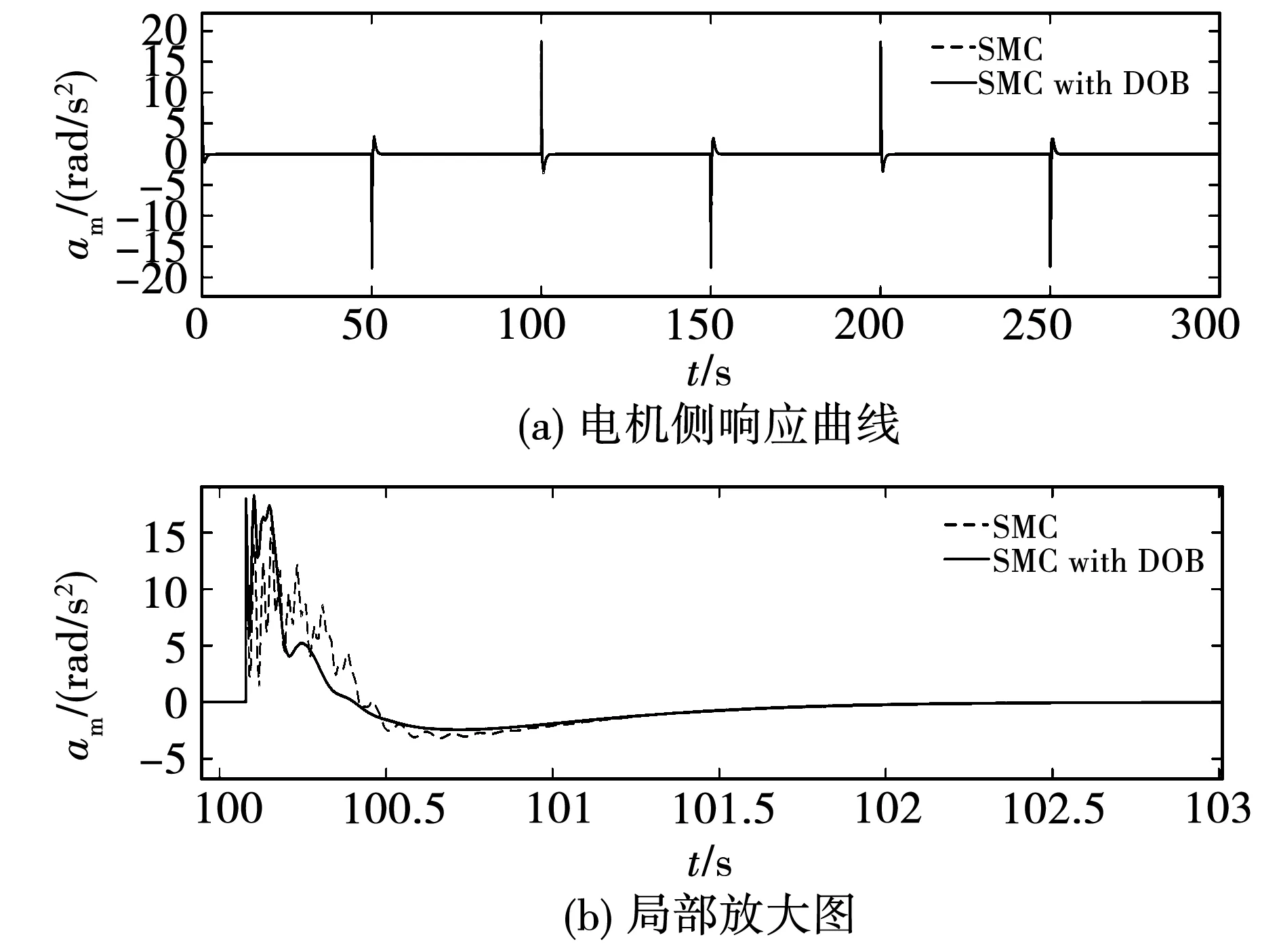
图10 三惯量系统谐振抑制效果Fig.10 Vibration suppression performance of 3-I system

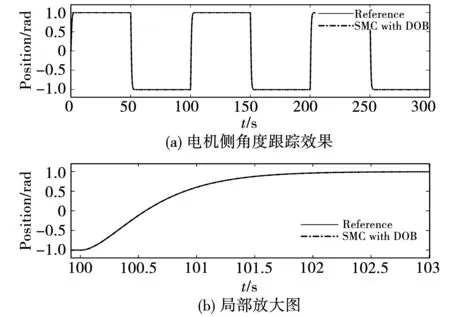
图11 双惯量系统跟踪效果Fig.11 Position tracking of 2-I system

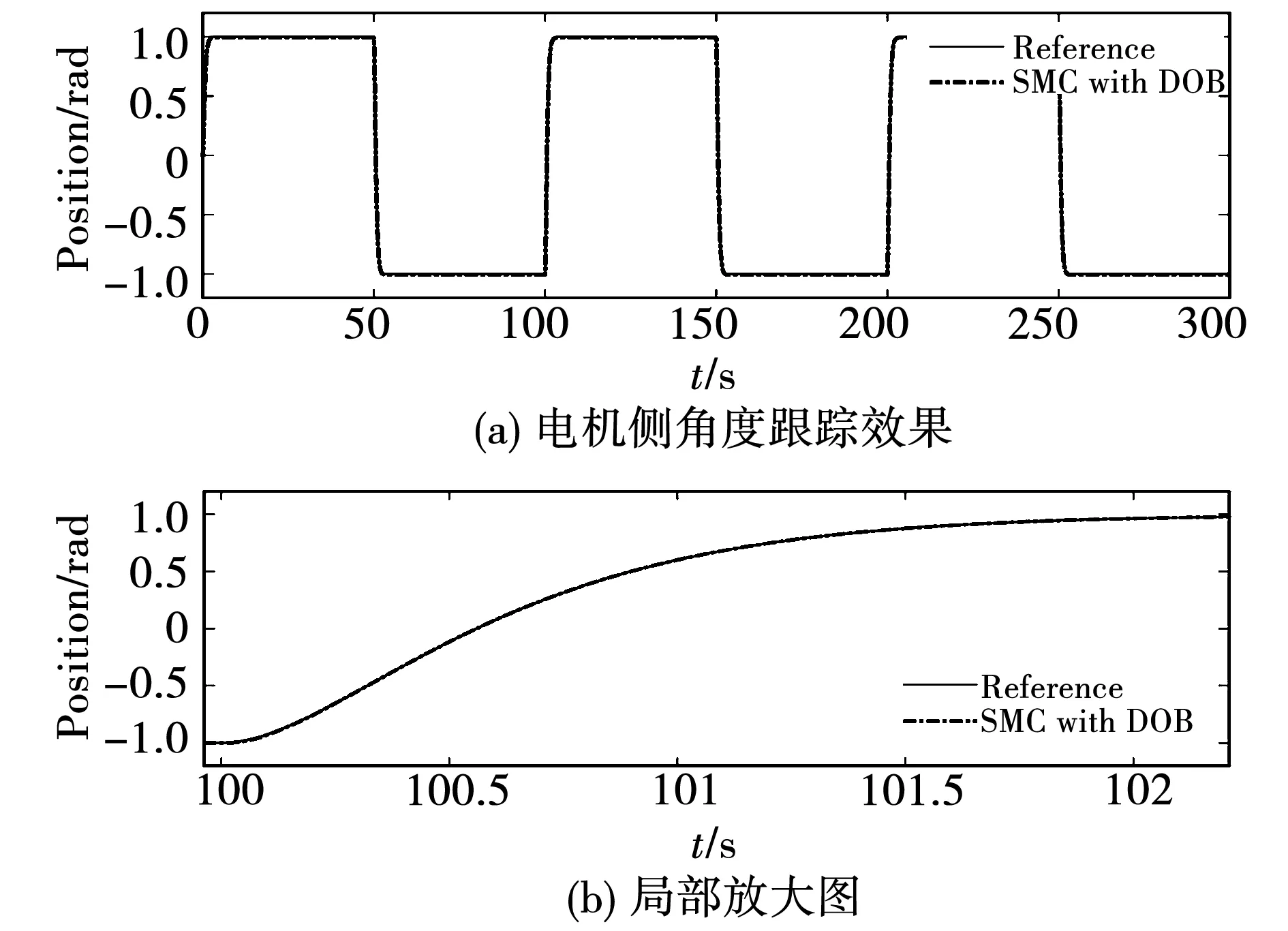
图12 三惯量系统跟踪效果Fig.12 Position tracking of 3-I system

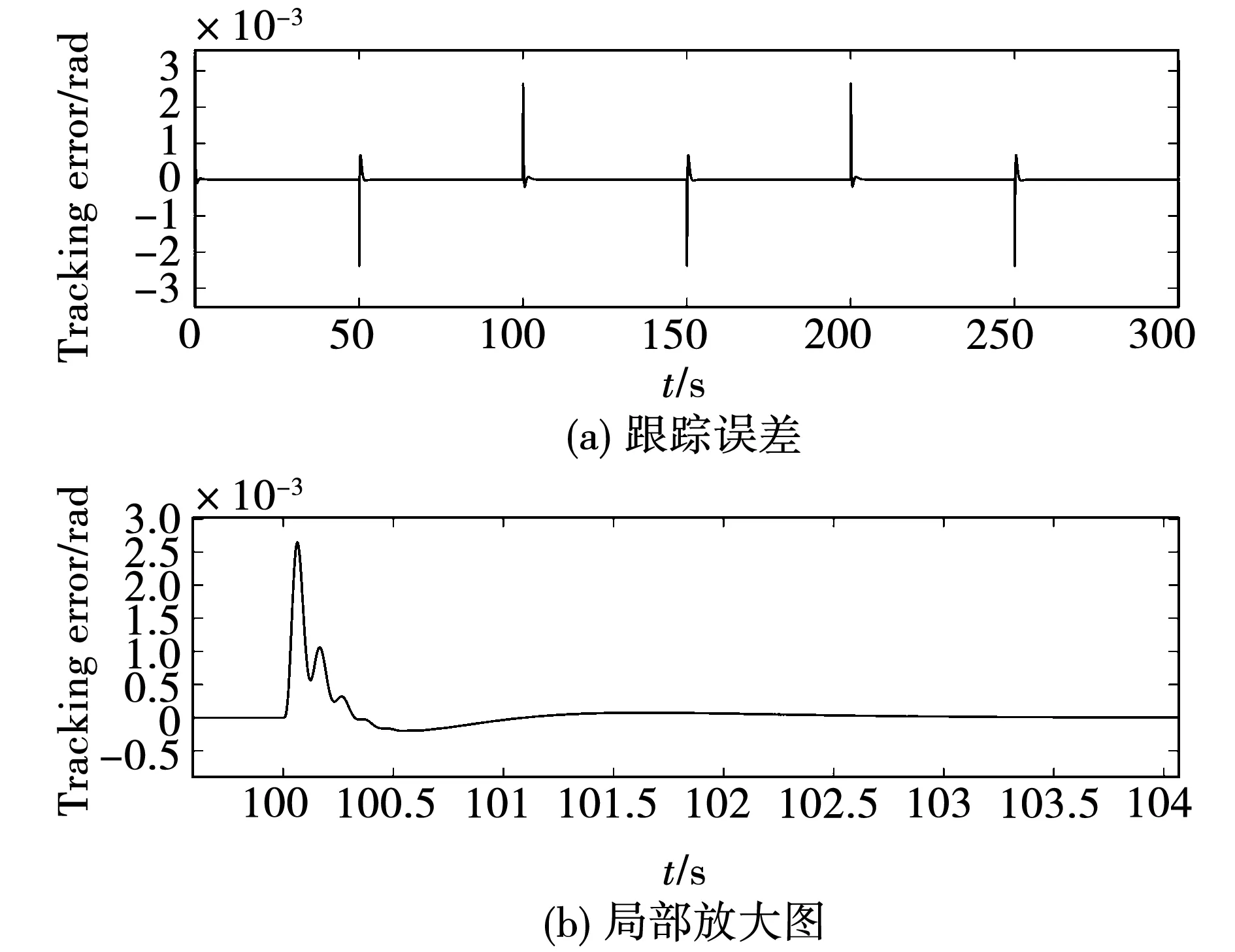
图13 双惯量系统跟踪误差Fig.13 Tracking error of 2-I system

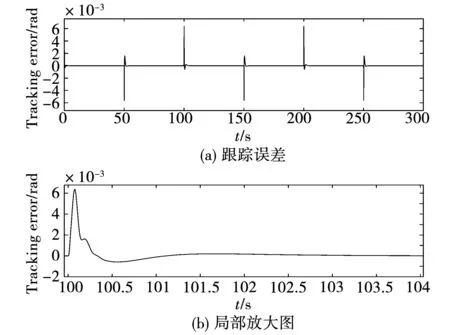
图14 三惯量系统跟踪误差Fig.14 Tracking error of 3-I system

图15～图18分别给出了控制输入和扰动估计效果。

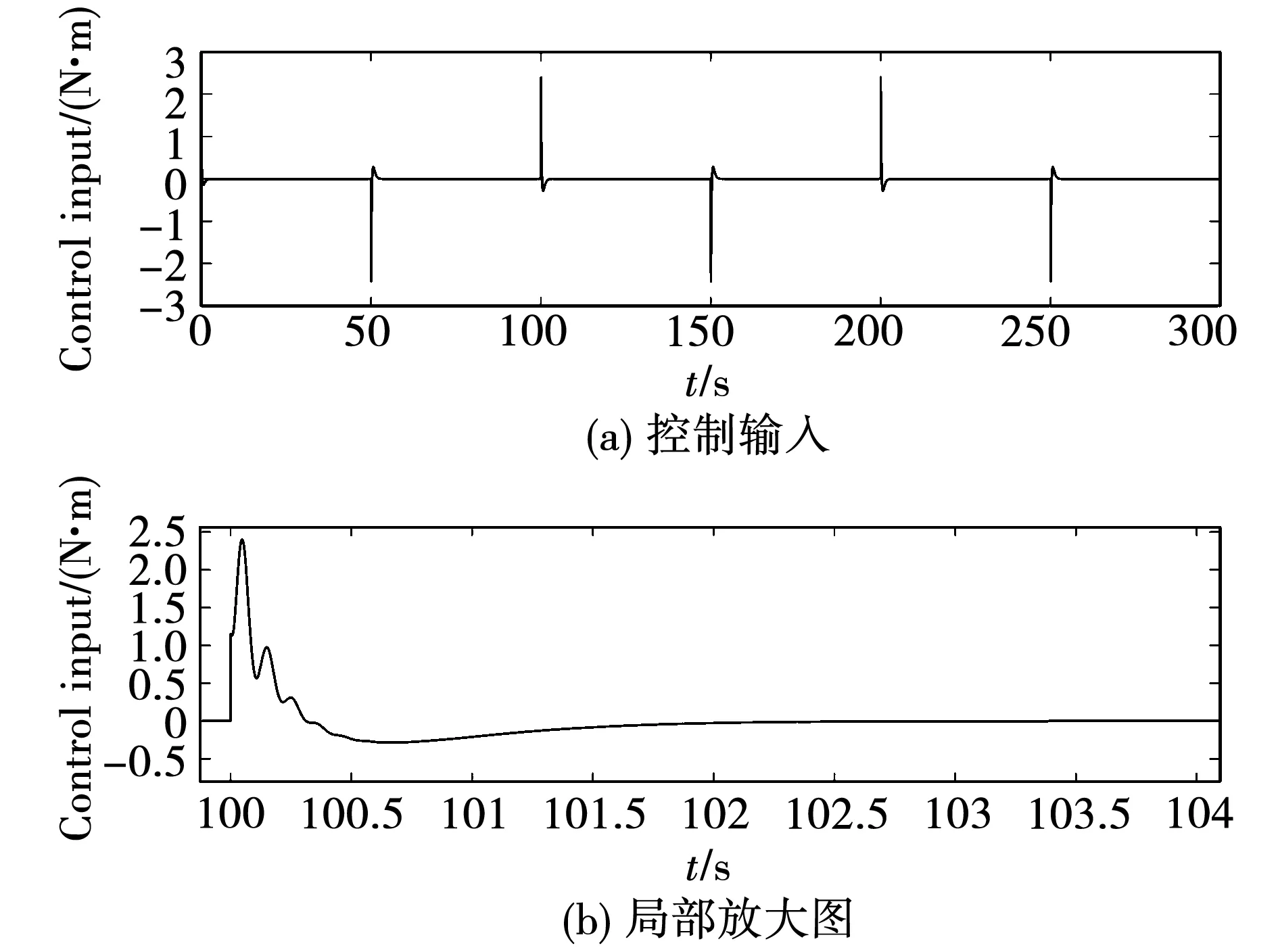
图15 双惯量系统控制输入Fig.15 Control signal of 2-I system

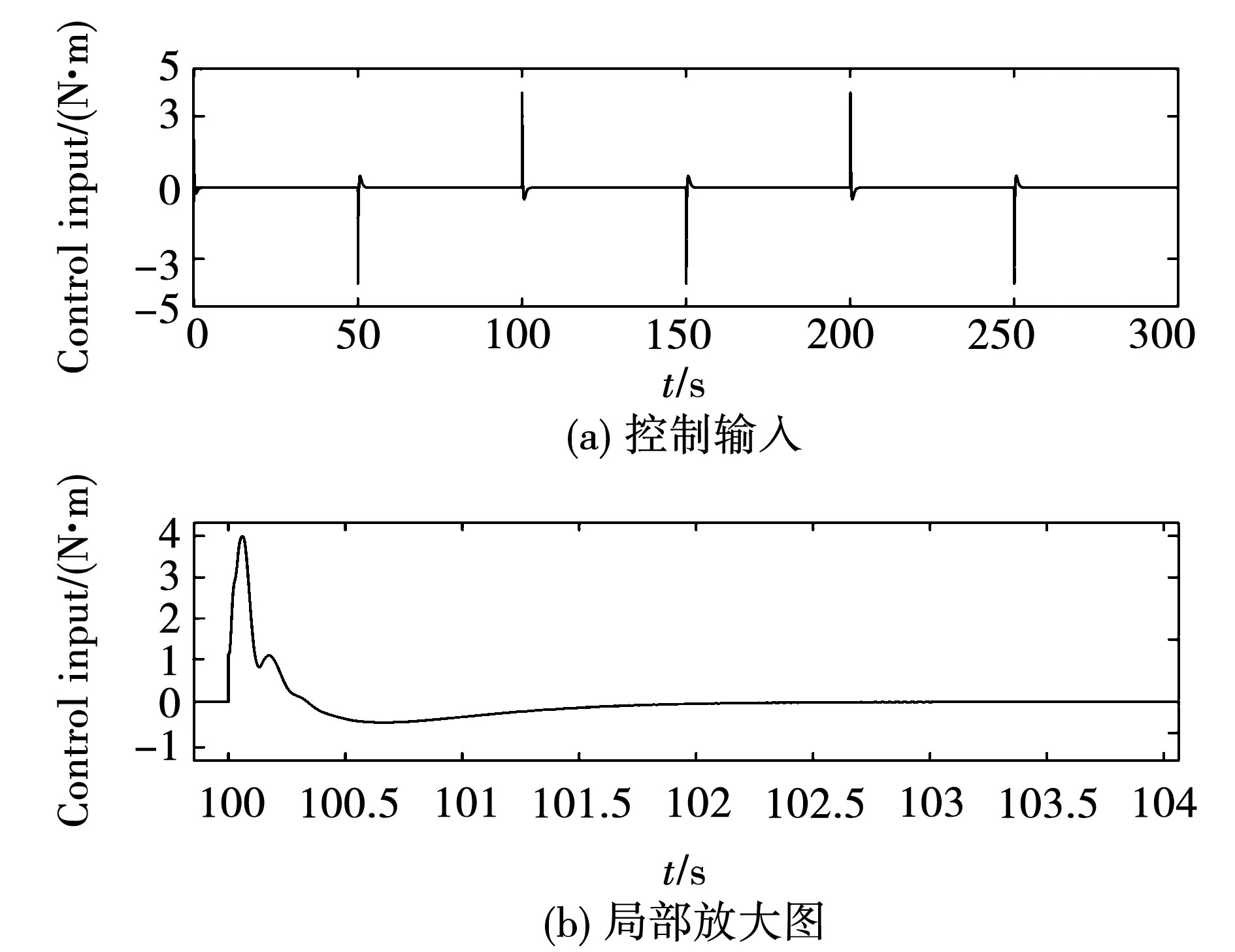
图16 三惯量系统控制输入Fig.16 Control signal of 3-I system

从图15和图16中可以看到，两类系统的控制输入信号较为光滑，无高频抖振现象。这表明本文所提出的新型滑模趋近律可以有效避免传统滑模控制中的抖振问题。图17和图18的结果表明了本文所涉及的DOB对电机侧扰动实现了有效的估计。

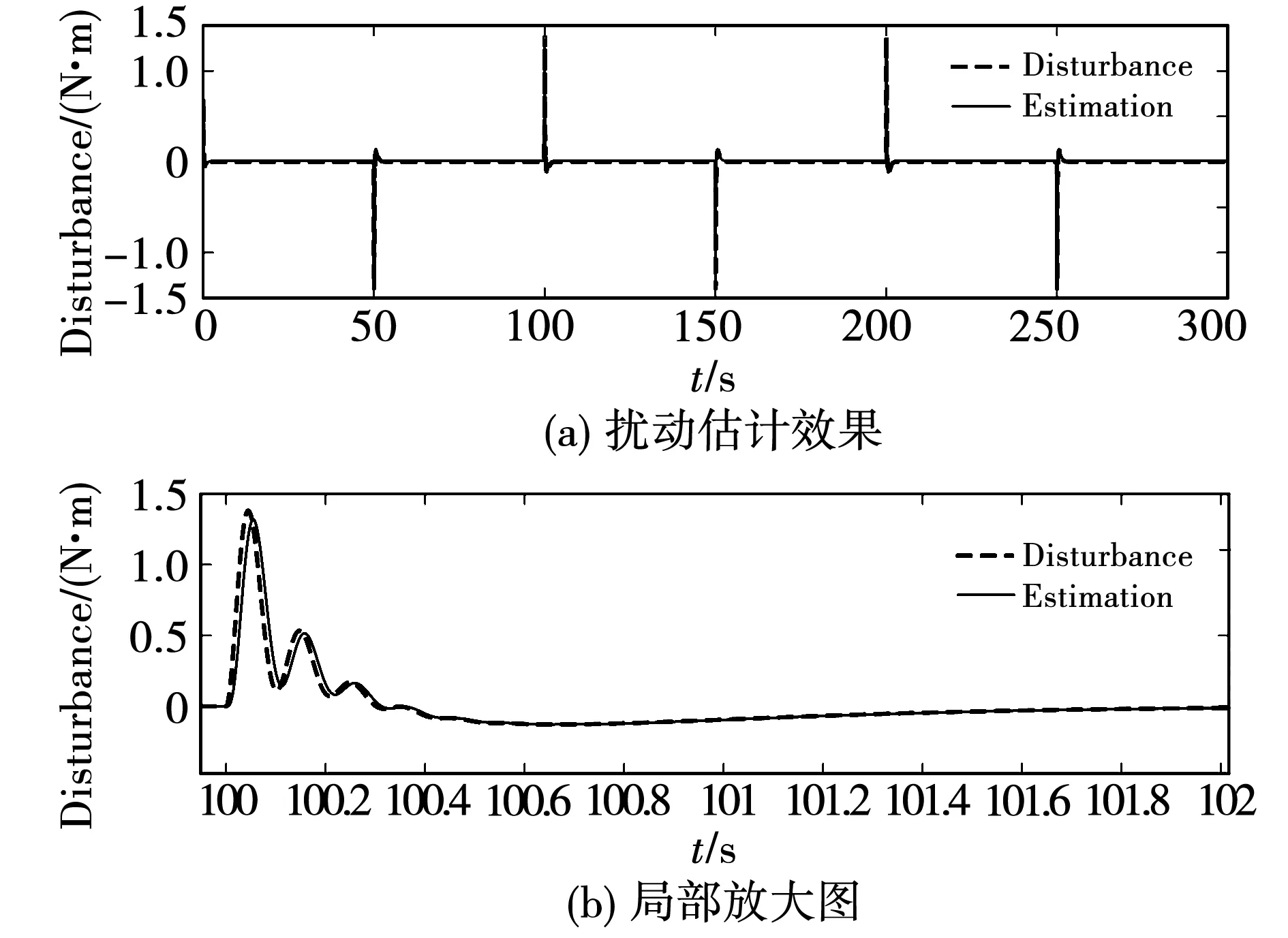
图17 双惯量系统扰动估计效果Fig.17 Disturbance estimation of 2-I system

此外，为了验证本文所提方法的鲁棒性，研究了当负载转动惯量JL和传动轴刚度系数Kc分别增加10%和减少10%时，系统的响应情况。同时，为了进一步说明本文所提出的滑模趋近律的优势，也设计了与传统的滑模趋近律对比仿真。对应地，传统滑模控制器设计为

(19)

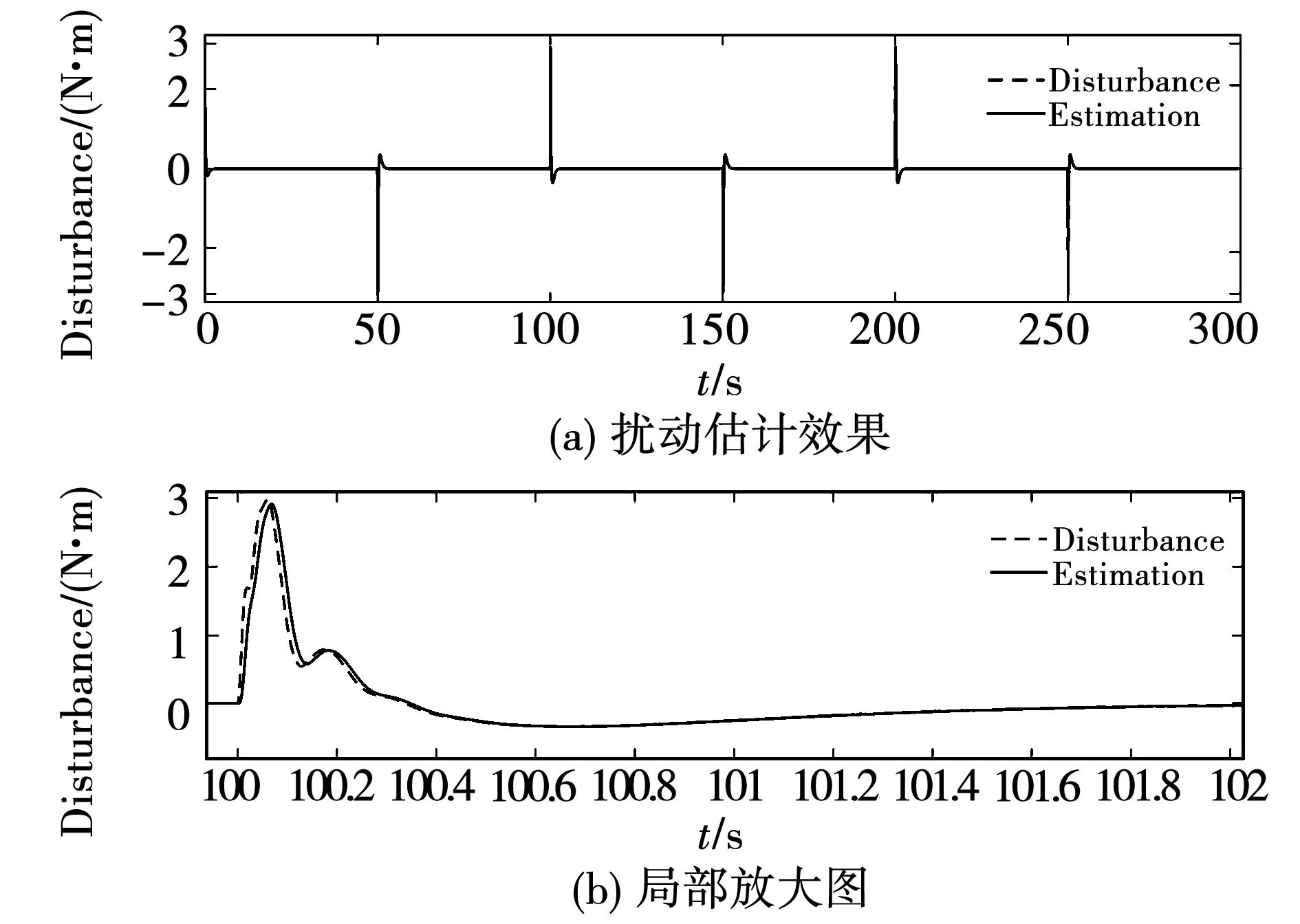
图18 三惯量系统扰动估计效果Fig.18 Disturbance estimation of 3-I system

在这里以双惯量系统为例，进行仿真分析，结果分别如图19和图20所示。从图19中可以看到，在参数变化10%的情况下，此时的系统相比于名义对象，在跟踪误差上只有小的波动，整体依然能保持良好的跟踪性能和谐振抑制效果。这表明，本文所提出的方法，能够有效地应对参数变化的情况。

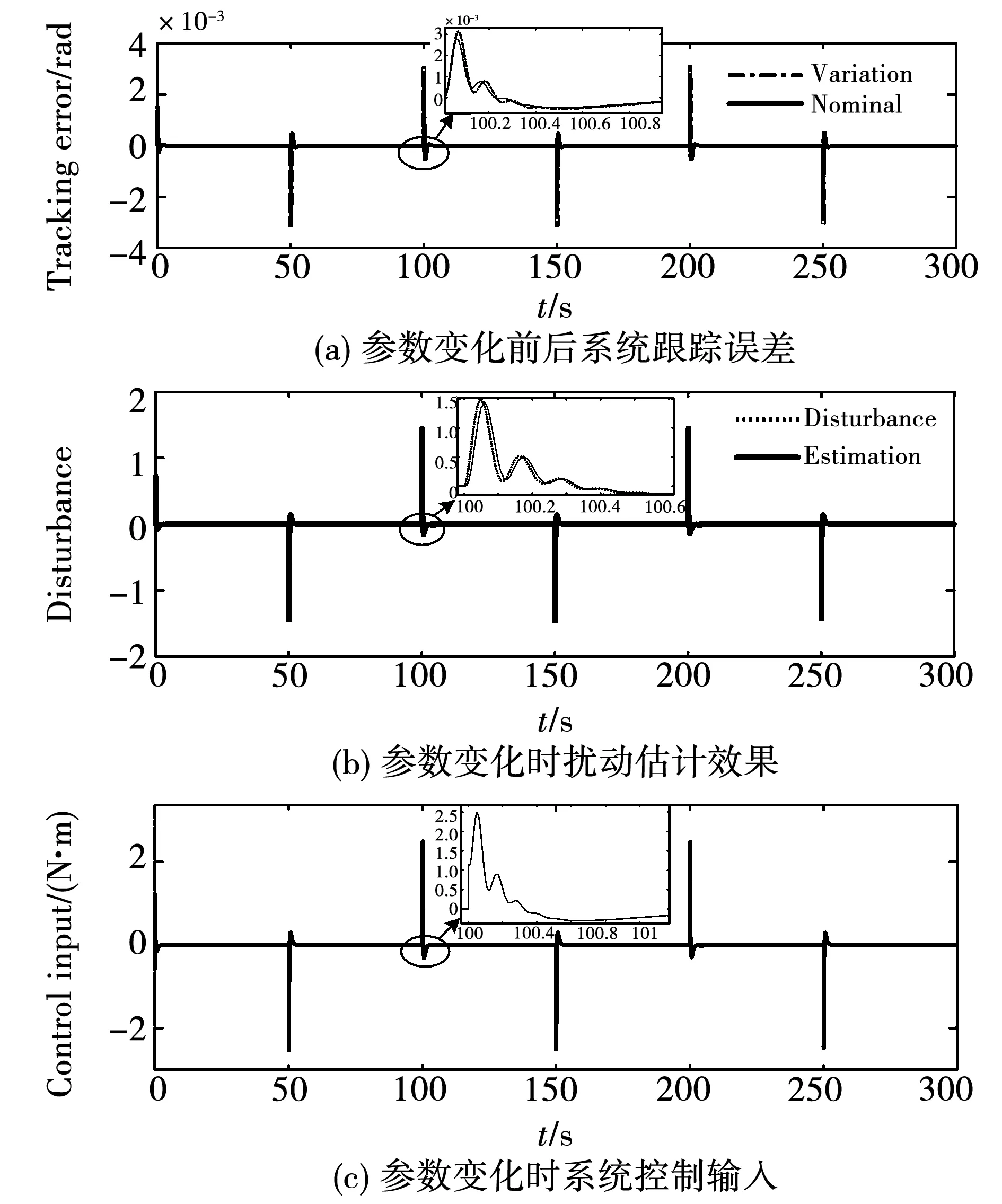
图19 模型参数变化时的仿真结果Fig.19 Simulation results for parameter variation

图20展示了在达到同样控制效果的前提下，相比于传统的滑模趋近律，本文所提出的新型滑模趋近律能够有效地避免抖振现象。可以验证，在三惯量系统中也是如此。

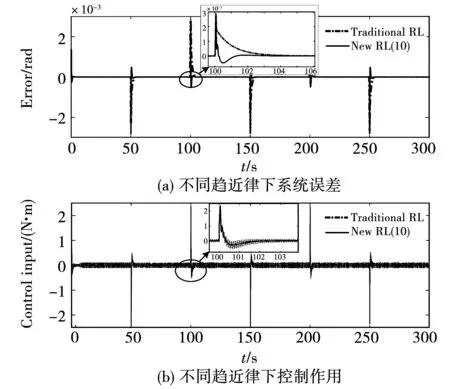
图20 与传统滑模趋近律对比结果Fig.20 Simulation results compared with traditional reaching law

4 结 论

本文针对双惯量系统和三惯量系统的谐振抑制问题，提出基于扰动观测器补偿的方法。根据系统的输入和输出信号，设计出的扰动观测器结构简单且易于实现，将系统等效为名义对象，使得系统中由于柔性传动轴和齿轮所引发的谐振现象得到了很好的抑制。为了消除传统滑模控制中的抖振现象，本文结合双曲函数提出一种新型滑模趋近律。基于以上设计，通过仿真验证了本文所提方法在两类系统中的有效性。

应该说明的是，本文主要针对系统的电机侧作为输出进行分析，而针对负载侧(如轴力矩、负载位置等)控制时则会有一些差异。因此，下一步工作将会针对这一点进行深入剖析。