虚拟同步发电机暂态稳定性分析与控制策略
2023-01-10王继磊张兴朱乔华韩峰付新鑫
王继磊,张兴,朱乔华,韩峰,付新鑫
(合肥工业大学 可再生能源接入电网技术国家地方联合工程实验室,安徽 合肥 230009)
0 引 言
随着以光伏、风电为代表的新能源并网比例不断攀升,传统电流控制型并网逆变器低惯性、欠阻尼的特征给电力系统带来的稳定性影响已不可忽视[1]。虚拟同步发电机(virtual synchronous generator,VSG)通过模拟同步发电机的运行特性,主动参与并网点电压支撑和电网频率调节,有望在高比例新能源并网系统中发挥重要作用[2]。
VSG提供电压、频率支撑的前提是VSG能够稳定并网运行。文献[3]建立了VSG的功率闭环小信号模型,并给出了控制参数的设计方法。文献[4-5]采用谐波线性化方法对VSG的输出阻抗进行建模,分析了VSG的序阻抗特性,研究了VSG与弱电网的交互稳定性问题。文献[6]建立了VSG的时域状态空间小信号模型,研究了控制参数、线路参数和滤波器参数等对系统稳定性的影响。然而,这些研究忽略了VSG的非线性特性,当系统工作点发生较大改变时,难以适用于系统暂态稳定性的评估。
相较于对小信号稳定性的充分研究,并网逆变器受到大信号干扰下的暂态稳定性问题尚在不断探索。文献[7-8]借鉴同步发电机的暂态稳定分析方法讨论了并网逆变器的暂态稳定性,提出相应的暂态控制方法。文献[9-10]研究了在电流限幅作用下,下垂控制型逆变器遭受大扰动时退化成电流控制型逆变器导致暂态失稳,提出一种带有电流限幅的并网逆变器暂态稳定性评估方法。文献[11]指出由于并网逆变器与同步发电机的实际动态特性不同,采用等面积判据分析逆变器暂态稳定性得到的结论存在偏差。文献[12-14]利用李雅普诺夫函数对并网逆变器进行暂态稳定性分析,然而非线性系统的李雅普诺夫函数一般较难被构造。上述文献在分析并网逆变器的暂态稳定性时,均未考虑控制参数、有功出力水平对VSG暂态稳定性的影响。文献[15]利用相平面法对不同控制策略的并网逆变器暂态稳定性进行分析,并讨论了控制器增益对暂态稳定性的影响。文献[16]提出一种针对直接电压式VSG的虚拟电阻和相量限流方法,有效抑制电网对称短路故障引起的电流冲击,却未考虑VSG的暂态稳定性。文献[17]提出一种基于暂态功角与电流灵活调控的VSG故障穿越方法,假设功角在故障期间不发生改变,但考虑到VSG的功率响应特性,实际功角会有所增加。
本文以VSG作为研究对象,采用相平面法分析电网故障下VSG的暂态稳定性,研究电压跌落深度、控制参数和有功出力水平对VSG暂态稳定性的影响,并讨论VSG暂态稳定的边界条件。在此基础上,提出一种根据电网故障程度自适应调节有功功率参考值的暂态控制策略,降低有功功率不平衡,从而避免暂态失稳。最后通过半实物仿真验证所提暂态控制策略的有效性。
1 VSG的数学模型
VSG主电路如图1(a)所示。图中:Lf和Cf分别为LC滤波器的电感和电容;Lg是电网阻抗;Vpcc、Eg和Vr分别为PCC电压、电网电压和桥臂侧输出电压;Udc是直流侧电压;i表示输出电流。
图1(b)为VSG的控制框图,Pref和Pe分别为有功功率参考值和瞬时有功功率;Qref和Qe分别为无功功率参考值和瞬时无功功率;J为虚拟惯性;Dp和Dq分别为有功功率下垂系数和无功功率下垂系数;ω和ωN分别代表VSG角频率和电网额定角频率;V和VN分别为VSG电压幅值和电压参考值;idref和iqref为电压控制环输出的电流参考值,erabc是调制波电压。
由于电压电流内环的动态响应远快于功率环,在功率环时间尺度下将电压电流内环视为具有理想跟踪性能的单位增益,即Vpcc为电压幅值(V)和输出相位(θ)的合成[15]。
由图1可知有功、无功功率环的控制方程分别为:
(1)
V=VN+Dq(Qref-Qe)。
(2)
对式(1)进行拉普拉斯变换可得到
(3)
定义VSG的功角为δ,其表达式为
(4)
将式(4)代入式(3)中,式(3)化为
(5)
图2为VSG并网运行时的等效电路图,其中ZVSG为VSG的输出阻抗。VSG的输出外特性等效成幅值为V,相位为δ的电压源。

图2 VSG的等效电路图Fig.2 Equivalent circuit diagram of VSG
由图2可得到VSG的输出功率为:
(6)
(7)
式中Xg=ωLg。
考虑到有功回路和无功回路之间的交叉耦合,将式(7)代入式(2),此时V的表达式为
(8)
由式(8)可以得到V关于δ的关系为

(9)
根据式(9)可以发现,当电网故障时,VSG的输出电压不是恒定值,其受到功角、电网电压幅值、无功下垂系数和电网阻抗等因素的影响。
2 VSG的暂态稳定性分析
等面积判据被广泛应用在同步发电机的暂态稳定性分析,但由于VSG与同步发电机相比,其阻尼系数是可控的,当阻尼系数过大时,使用等面积判据分析VSG暂态稳定性得到的结果不准确[11]。因此,本节采用相平面法对VSG的暂态稳定性影响因素进行分析,结合相平面法所得数值解,通过扩展等面积法给出了暂态稳定的边界条件。
2.1 相平面法
相平面法是研究一阶、二阶非线性系统的一种图像方法,其主要思想是在相平面上根据初始条件绘制非线性系统的运动轨迹,从而研究非线性系统的稳定性和动态性能。
设二阶非线性系统为
x″=f(x,x′)。
(10)
式中f是x(t)和x′(t)对应的非线性函数。
相平面图如图3所示,当x′(t)>0时,x(t)不断增加。当x′(t)<0时,x(t)不断减小。即在上半平面中,工作点沿相轨迹向x轴正方向移动,上半部分相轨迹箭头向右,下半平面相轨迹箭头向左,也就是说,相平面图在相轨迹上总是按顺时针方向运动的。只有当x′(t)=0时,系统工作在稳定状态,否则系统工作点将持续变化。
2.2 VSG暂态稳定性的影响因素
电网发生短路故障导致电网电压跌落,VSG有功功率输出减小。由式(5)可知,VSG功角将持续增大直至δ′(t)=0,因此VSG在遭受大干扰情况下的会出现类似传统同步发电机的功角失稳。为了避免这一状况,首先分析VSG暂态稳定性的影响因素。
由将式(6)代入式(5)进一步可得

(11)
由式(11)可以得到VSG受到大扰动后的相平面图。图4展示了电压跌落深度对VSG暂态稳定性的影响,a点表示故障前系统的稳态工作点,b点和c点代表系统在不同程度电网故障后的稳态工作点。当电网电压跌落至0.6 pu和0.4 pu时,功角先增大后减小,最终分别收敛至b点和c点,系统稳定。随着电网电压进一步降低至0.2 pu,Pref>Pemax=1.5EV/Xg,VSG不存在稳态工作点,δ′(t)始终大于0,VSG暂态失稳。

图4 电网电压跌落深度对VSG相平面图的影响Fig.4 Influence of grid voltage drop depth on VSG phase portrait
在图5中电网电压跌落至0.4 pu,图5(a)中J分别为0.02和0.05 kg·m2时,功角从0.26 rad增加到1.11 rad,不同J的VSG在故障前后有相同的稳态工作点。但J的增大导致功角超调量增大,影响系统到达稳态工作点的动态过程。当J=0.1 kg·m2时,δ′(t)>0,功角持续增大,VSG不能到达稳态工作点,从而暂态失稳。Dp对VSG暂态稳定性的影响如图5(b)所示,正常工况下VSG稳定运行在a点,当Dp=30时,故障后VSG到达b点,功角基本无超调。Dp减小至20时VSG虽然最终到达b点,但功角超调量增加。当Dp进一步减小至10时,功角持续发散,VSG发生暂态失稳。图5(c)表明即使电网电压跌落深度相同,随着Dq的变化,VSG的稳态工作点会发生变化,由式(6)和式(9)可知这是因为Dq的变化影响了VSG的输出电压。随着Dq的增大,故障后系统稳态工作点对应的功角稳态值和暂态期间功角最大值都增大。当Dq增大至0.003时,VSG发生暂态失稳。由上述分析可知,较小的J、较大的Dp以及较小的Dq可以提高VSG的暂态稳定性。

图5 控制参数对VSG相平面图的影响(E=0.4 pu)Fig.5 Influence of control parameters on on VSG phase portrait(E=0.4 pu)
图6展示了有功功率参考值对VSG相平面图的影响,a、b、c点分别对应正常工况下有功功率指令Pref为5、12、20 kW的系统稳态工作点。随着Pref的增大,VSG稳态工作点对应的功角也增大。当电网电压跌落至0.2 pu,当Pref=5 kW和Pref=12 kW时,VSG的功角增大,最终分别在d点和e点稳定运行,功角不再发生变化。当Pref=20 kW时,Pref>Pemax,VSG不存在稳态工作点。故障后VSG的功角不断增大,δ′(t)>0,系统暂态失稳。
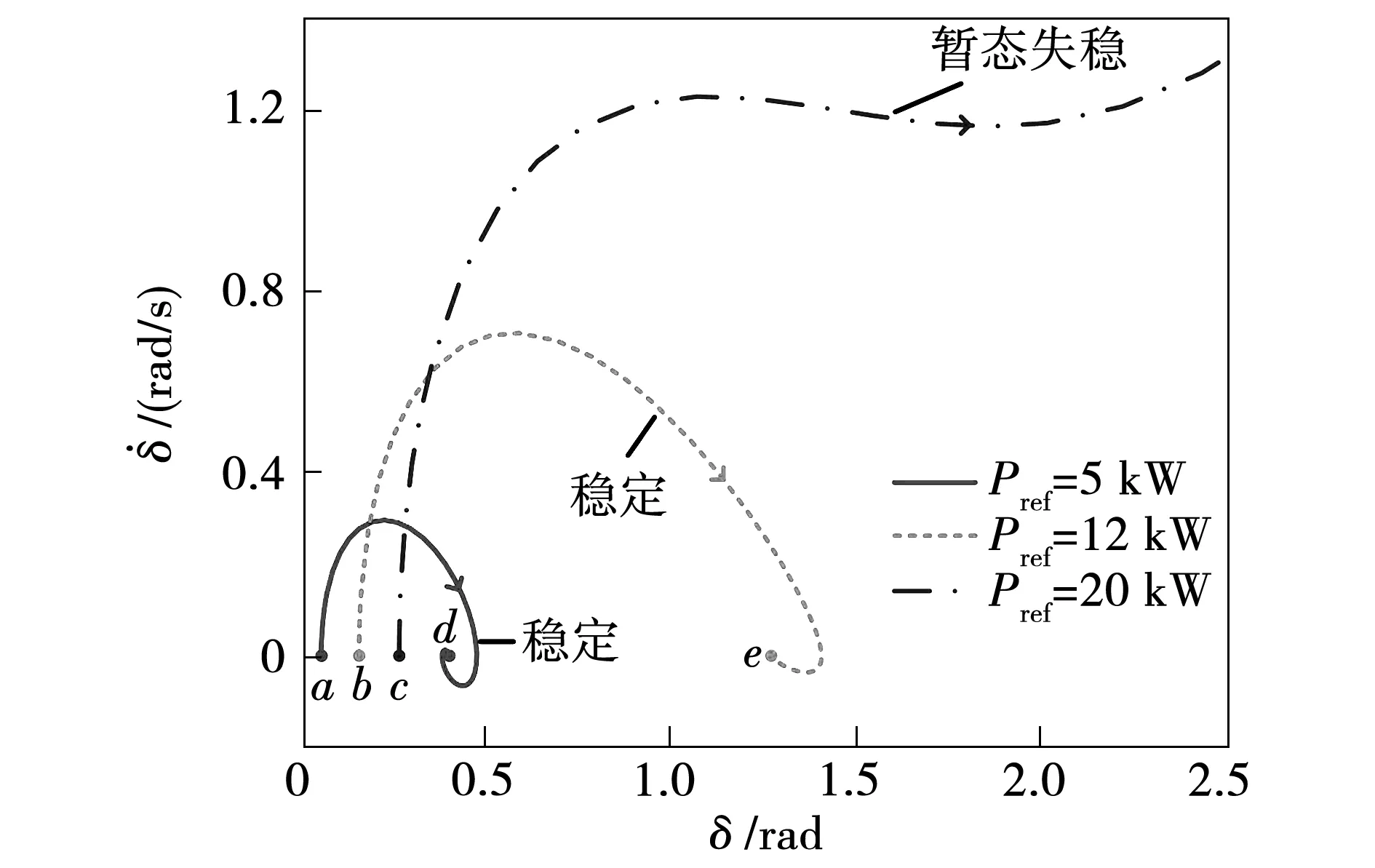
图6 有功功率参考值对VSG相平面图的影响(E=0.2 pu)Fig.6 Influence of active power reference on VSG phase portrait(E=0.2 pu)
2.3 VSG暂态稳定的边界条件
相平面分析法本质上是一种数值算法,可以针对特定系统分析暂态稳定性,实现面向系统的参数设计,具有工程价值,缺点是不具备物理意义。为此,针对传统等面积判据和相平面分析法的不足,根据扩展等面积法分析VSG暂态稳定的边界条件。
定义Pn=Pref-Ddδ/dt,根据式(11)所得数值解,联立式(1),VSG的功角曲线如图7所示。图7(a)中电网短路故障导致Pe下降,Pn随dδ/dt动态变化,此时Pn
图7(b)中,电网短路故障导致功角由δ0增加至δ1后,Δω减小,在a点处Δω=0,然后δ开始减小。功角振荡过程结束后,VSG最终稳定运行在c点。
因此,考虑阻尼后,基于式(11)所得到的数值解,VSG暂态稳定需要满足

(12)
3 VSG的暂态控制策略
电网故障导致Pe

图7 基于扩展等面积法的VSG功角曲线Fig.7 VSG power angle curve based on extended equal area method
定义有功功率差值ΔP=Pref-Pe,VSG与电网的角频率差值Δω=ω-ωg,由式(1)可得
(13)
解线性微分方程式(13)得到
(14)
则电网故障发生后功角变化量为
(15)
电网故障前VSG有功功率输出为
(16)
电网故障后功角增大,δF=δN+Δδ,则此时VSG有功功率输出为
(17)
式中:PeN是正常工况下VSG有功功率输出;PeF是电网发生故障后VSG有功功率输出;δN是电网故障前的VSG功角;δF是电网故障后的VSG功角;VN和EN分别为正常工况下VSG输出电压和电网电压;VF和EF分别为电网故障后VSG输出电压和电网电压。
假设电网发生故障后,VSG输出有功功率和有功功率指令值近似相等,即δF≈δN,Δδ被认为是一个很小的值,此时cosΔδ≈1,sinΔδ≈Δδ,式(17)可进一步推导表示为
(18)
结合式(17),电网故障前后VSG有功功率输出的关系为
(19)
当电网故障后,根据式(19)适当调节VSG有功功率参考值,避免功角持续增加,设置电网发生故障后的有功功率参考值为
(20)
联立式(9)、式(11)和式(20)可得
(21)
图8是采用所提暂态控制策略的VSG有功控制框图。由于实际电网电压幅值在一定范围内波动,为避免有功功率随之频繁波动,系统检测到电压幅值低于阈值时所提暂态控制策略生效,本文中设置电压阈值为90%EN。
考虑到实际中难以获取远端电网电压信息,其实时变化信息不能准确掌握。因此需要研究不依赖电网电压如何实现所提暂态控制策略。

图8 采用所提暂态控制策略的VSG有功控制环框图Fig.8 VSG active power control loop adopts the proposed transient control strategy
根据图2所示,考虑VSG分压时远端电网电压可表示[18]为
(22)
图9展示了采用所提暂态控制策略的VSG在电压跌落至0.2 pu时的相平面图,稳态运行功率为20 kW。由于采用所提暂态控制策略,故障期间根据式 (20)功率等级被自适应调整为3.53 kW。正常情况下VSG稳定工作在a点,对应功角为0.27 rad。电网发生故障后,VSG功角增加至0.28 rad。结合图6可知,采用所提暂态控制策略大大减小了功角变化量,使VSG在电网严重故障时也存在稳态工作点,提高了VSG的暂态稳定性。

图9 采用所提暂态控制策略的VSG相平面图(E=0.2 pu)Fig.9 Influence of active power reference on VSG phase portrait(E=0.2 pu)
图10(a)为未采用所提暂态控制策略的VSG功角曲线,虽然Pn随dδ/dt动态变化,相较于Pref有所下降,但S加速>S减速,根据式(12)可知,此时不满足VSG的暂态稳定边界条件,VSG的功角持续增加,导致暂态失稳。图10(b)中采用所提暂态控制策略后,自适应调节Pref,使得Pn≈Pe,S加速< 图10 VSG的功角曲线(E=0.2 pu)Fig.10 Power angle curve of VSG(E=0.2 pu) 为了验证理论分析的正确性,本节基于RT-LAB的半实物仿真平台进行实验验证,平台如图11所示。根据图1搭建系统模型,在TI公司的DSP-TMS320F28335进行算法实现,系统参数如表1所示。 图11 基于RT-LAB的半实物仿真平台Fig.11 Hardware-in-the-loop simulation platform based on RT-LAB 表1 系统参数Table 1 System parameters 设置Pref=20 kW,Qref=0。当电压跌落深度不同时VSG的暂态响应如图12所示,由图12(a)可以发现正常工况下VSG的功角为0.27 rad,在电网电压跌落至0.4 pu情况下系统保持稳定,故障发生后的功角稳态值为1.11 rad,功角最大值为1.35 rad。图12(b)中VSG在电网电压跌落至0.2 pu后功角持续增大,有功功率、电流和功角发生振荡,VSG暂态失稳。 图12 电网故障时VSG的暂态响应 Fig.12 Transient response of VSG during grid fault 当电网电压跌落至0.4 pu,不同J下VSG的暂态响应波形如图13所示,正常工况下VSG功角都是0.27 rad。从图13(a)中发现,当J=0.02 kg·m2时,故障发生后的功角稳态值为1.11 rad,动态过程基本无超调。图13(b)中J=0.1 kg·m2,电压跌落导致功角持续增大,有功功率、电流和功角发生振荡,VSG暂态失稳。 图13 不同虚拟惯性下VSG的暂态响应(E=0.4 pu)Fig.13 Transient response of VSG under different virtual inertia(E=0.4 pu) 图14为不同有功下垂系数下VSG暂态响应波形,正常工况下VSG功角都是0.27 rad。图14(a)中Dp=30时在故障暂态期间功角基本无超调,故障后的功角稳态值为1.11 rad。图14(b)中Dp减小至10,功角持续增加,VSG发生暂态失稳。 图15为改变无功下垂系数时VSG的暂态响应波形,从图15(a)中观察到当Dq=0.001时故障后功角的稳态值为0.93 rad,故障暂态期间功角最大值为1.12 rad。对比图12(a),Dq增大使得功角的稳态值和暂态期间最大值有所增大。图15(b)中Dq为0.003,功角持续增大,电网发生故障后有功功率、电流和功角振荡,VSG暂态失稳。 图14 不同有功下垂系数下VSG的暂态响应(E=0.4 pu)Fig.14 Transient response of VSG under different active droop coefficients(E=0.4 pu) 图15 不同无功下垂系数下VSG的暂态响应(E=0.4 pu)Fig.15 Transient response of VSG under different reactive droop coefficients(E=0.4 pu) 图16为采用所提控制策略VSG的暂态响应实验波形,电网电压跌落至0.2 pu。从图中观察到电网故障后由于根据电网跌落程度自适应调整有功功率参考值,降低了有功功率的不平衡。与图12(b)相比,故障后功角略有增加,避免了暂态失稳,VSG在电网发生严重故障情况下仍能保持稳定。 图16 采用所提控制策略VSG的暂态响应(E=0.2 pu)Fig.16 Transient response of VSG using the proposed control strategy(E=0.2 pu) 电网对称故障相较于不对称故障危害更为严重,但不对称故障较为常见。图17中Ea和Eb分别跌落至0.4 pu和0.6 pu,采用所提暂态控制策略后,有功功率输出降低,功角略有增加,说明所提暂态控制策略在电网不平衡故障仍然适用。 图17 采用所提控制策略不平衡故障下VSG的暂态响应Fig.17 Transient response of VSG under unbalanced fault with the proposed control strategy 本文建立了VSG的数学模型,采用相平面法分析了在电网故障下VSG的暂态稳定性,研究了VSG暂态失稳的边界条件,并进行半实物仿真验证。研究结果表明: 1)电压跌落程度越严重,系统越容易暂态失稳。VSG的暂态稳定性与控制参数有关,J越大、Dp越小,功角超调量越大,降低了系统的暂态稳定裕度。Dq不仅影响暂态动态过程,也会改变稳态工作点,并且Dq增大会恶化VSG的暂态稳定性。 2)VSG的暂态失稳是有功功率不平衡导致功角持续增大导致的。为了避免VSG发生暂态功角失稳,提出一种自适应调节有功功率参考值的暂态控制策略,提高了VSG的暂态稳定性。 本文的重点是分析VSG的暂态稳定性并提出暂态控制策略。由实验波形发现电网故障导致VSG出现电流冲击现象,文献[17]通过降低电压参考值抑制电流冲击,但这会削弱VSG的电压支撑特性,影响VSG的小信号稳定性。因此VSG的短路电流抑制方法将在后续进一步研究。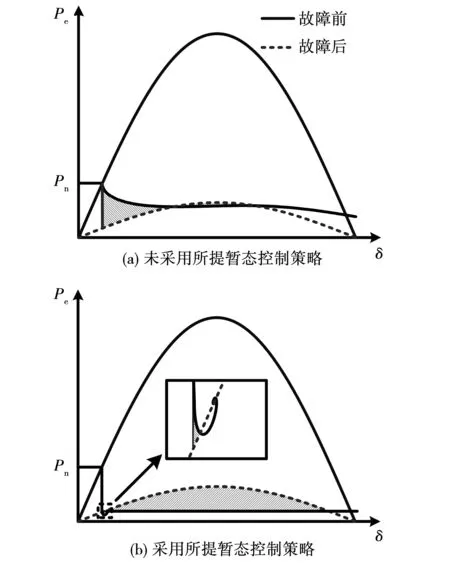
4 半实物仿真验证








5 结 论
