“都” 与否定极性项的分布及单调性推演
2023-01-10姚从军李冬晴
姚从军,李冬晴
(湘潭大学哲学系,湖南湘潭 411105)
一、引言
“一阶逻辑在数学领域内运用显然是成功的,但也严重地淡化了逻辑同自然语言的联系。除了时态逻辑和模态逻辑外,过去25年的模型论研究几乎完全从纯数学理论那里获取题材,从而变得越来越专业化,离自然语言也越来越遥远。一阶逻辑在数学领域内的成功运用同样也助长了一种错误观念,即逻辑的规律是自足的,或者说是数学的部分,而并非语言和语言使用的性质。”[1]形式语言中的逻辑量词同自然语言中的限定词及名词短语一样,仅仅只是量词理论的特例。正如蒙太格 “通用语法” 思想所揭示的那样,逻辑的人工符号也是一种跟自然语言类似的语言,也是广义语言学所研究的对象,逻辑仅仅是这种语言学的一个部分。在谈及广义量词理论时,巴威斯(Barwise,1981)写道: “在不甚清楚的情况下,人们有时总相信存在某个固定不变的公理系统和逻辑规则,相信自然语言中的推理是有效的,当且仅当它能够通过这些公理及规则被形式化地说明。但实际的情况却完全不是这样。”[1]判定一个推理是否正确,前提的真是否蕴涵结论的真,母语说话者的直觉是最基本、最原始的标准。因此,教人们怎样去推理的逻辑应该根据母语说话者关于推理的直觉去重新审视传统模型论语义学所谓的 “逻辑有效” 概念。对自然语言限定词、名词短语、量化副词、否定极性项等词项的语义性质进行深入挖掘,就是把握这些直觉的尝试。如同对广义量词的研究一样,对 “都” 和否定极性项的分布进行深入研究可以促使我们对 “逻辑有效” 概念进行重新思考,扩展有效逻辑推理式的阵营,具有重要的启发性和引领作用。
二、自然语言的否定极性项及其语境敏感性
对自然语言中的极性现象的研究最早始于克利马(Klima,1964)。克利马在研究英语否定问题时提出了极性敏感(Polarity Sensitivity)(1)的概念。他发现有些英语单词或短语对语境非常敏感,这些词项只有在肯定或否定的语境中才能够得到解释,并把这样的词项称为极性项(Polarity Items,PI)。[2]20 世纪60年代以来,学者们对极性项的研究多侧重于否定极性项(Negative Polarity Items,NPIs)。所谓否定极性项是指只能在否定语境中才能得到允准的词项。否定极性项可以是限定词、副词,也可以是动词。在英语中,限定词any是最常见的否定极性项。any除在否定算子的辖域内获得允准外,在具有否定意味的动词的辖域、全称量词的左论元、条件句的前件和疑问句中都可以得到允准。
① a.John doesn’t like any farmer.(否定句)
b.Ann denies Bill drank any water.(否定意味的动词)
c.Everyone who has ever taken a math class passed the entrance examination.(全称量词左论元)
d.If he ever wants to visit us,he should give us a call.(条件句前件)
e.How does any body stand this?(疑问句)
与英语相比,汉语中也存在很多否定极性项,比较常见的是与英语 “any+np” 平行的限定词 “任何+np” 和与极小词(2)“a+np” 平行的 “一量(np)” 。此外,还有光杆疑问词、副词等,如:
② a.不论干什么活,他都十分卖力。(光杆疑问词)
b.世界上没有任何一成不变的东西。(限定词)
c.刘胡兰坚强地没有流一滴眼泪。(极小词)
d.邱少云从来都不知道什么叫 “放弃” 。(副词)
与英语中的否定极性项有所区别,汉语中的否定极性项不仅需要得到否定成分的允准,在有些情况下还要得到 “都” 的允准,如 “任何困难和挫折都无法阻挡我们前进的脚步” 。也就是说,否定极性项需要全称量化算子 “都” 和 “不、没有、并非” 等否定算子的双重允准。为什么会生成 “NPI+都+Neg” 这样的结构呢?袁毓林(2007)认为 “都” 具有隐性否定的语义功能,这也是 “都” 允准否定极性项的根源。[3]袁毓林的形式验证如下:
③ a.他写小说。→★(3)下同他从来写小说。
b.他不写小说。→他从来不写小说。
c.他都写小说。→他从来都写小说。
d.他写小说之外的文章。→★他从来写小说之外的文章。
e.他不写小说之外的文章。→他从来不写小说之外的文章。[3]
③a “他从来写小说” 不合语法,因为否定极性项 “从来” 只能在否定的语境中才能得到允准。然而,③c “他从来都写小说” 合语法, “从来” 在肯定的语境中也得到了允准。因此,袁毓林认为 “都” 具有否定的语义性质。在现代汉语中人们判定某一词或词语是不是否定极性项是看它是否只在否定语境中得到允准。由此,袁毓林从形式上验证出 “都” 和否定词 “不” 一样,二者都具有允准否定极性项的功能,都能创造否定性语境,两者唯一的差别是 “不” 的否定功能是显性的, “都” 的否定性是隐性的。这样一来, “都” 的隐性否定便可以得到合理的解释。但这样的验证忽视了一个问题:否定极性副词 “从来” 不仅可以用在否定句,还可以用在肯定句。例如:
④ a.我们老板从来就是一个人说的算。
b.用户从来就应该看到商家的营业执照。
由④可以看出, “从来” 可以不需要与否定算子连用。③a中 “他从来写小说” 虽然被标记为错误语句,但不代表 “从来” 只用在否定句中,③b也只是 “从来” 的常见用法。
⑤ a.他从来就不是写小说的料。
b.他从来就是写小说的料。
c.他从来就都是写小说的料。
d.他从来就都不是写小说的料。
从⑤中可以看出, “都” 和 “从来” 既可以用在肯定句也可以用在否定句。因此,拿③中b、c两句证明 “都” 和 “不” 都能创造否定性语境还有待商榷。但袁毓林提供了一个很好的思路,如果能够调查到 “都” 在所有否定极性项中的分布,找出 “都” 和否定算子必须出现的情况,那么就可以进行类比分析,从而找出 “都” 单调推理的语义性质。
三、 “都” 与否定极性项的分布
(一) “都” 与否定极性光杆疑问词的分布
光杆疑问词 “什么” 可以用在疑问句中、否定算子之后、在否定算子之前(在疑问句中)。此外,它还可以和 “都” 连用,和 “都+否定” 连用。
① a.什么人来过?(NPI)
b.没有什么学生想加入我们的团队。(Neg+NPI)
c.什么人没有?(NPI+Neg)
d.我什么书都看。(NPI+都)
e.什么人都没来参加此次会议。(NPI+都+Neg)
①a中,光杆疑问词 “什么” 可以用在疑问句,但是不能单独用在肯定句,如: “*什么人” 。①b是 “什么” 的常见用法,此时, “什么学生” 在否定算子的辖域内。①d表明, “什么人” 受到了 “都” 的影响,但没有受到否定算子的影响。①c中,在没有 “都” 的条件下, “什么+np+否定算子” 句式可以用在疑问句,但不能用在肯定句。由此可见,在排除疑问句的条件下,光杆疑问词在前,光杆疑问词要与 “都” 共现;在疑问句中,光杆疑问词要与否定算子共现。
(二) “都” 与否定极性限定词的分布
汉语中限定性否定极性项构成的不定指名词短语是 “任何+np” ,否定算子是通过否定np中的所有成分以达到对整个范围的否定。英语中的 “any+np” 和汉语中的 “任何+np” 有相似的句法要求:否定算子需在否定极性项之前。例如:
② a.Don’t let any people enter Hoh Xil.
b.★Let any people enter Hoh Xil.
c.不许让任何人进入可可西里。(Neg+NPI)
d.★让任何人进入可可西里。(NPI)
从②a和②c可以看出,否定算子必须在限定词之前,限定词必须在否定算子的辖域内。此外,当否定算子位于否定极性项之后,语句也不合语法。例如:
③ a.*Anything I don’t like eating.
b.★任何东西我不喜欢吃。
③中,否定算子位于限定词之后,限定词没有在否定算子的辖域内,因此不合语法。但英语中的 “any+np” 和汉语中的 “任何+np” 有一个不同点:汉语 “任何+np+都+Neg” 可生成合法语句。例如:
④ a.★任何士兵都死了。(NPI+都)
b.★任何士兵没有死。(NPI+Neg)
c.任何士兵都没有死。(NPI+都+Neg)
④c构成的 “任何+np+都+Neg” 语序为合法语句,但在④a和④b中, “任何+都” 和 “任何+否定” 都不合语法。由此可以看出, “任何” 需要 “都” 和否定算子的双重允准。但是在道义命题中, “任何” 和 “都” 可以连用,在双重否定的道义命题中, “都” 可以省略。道义命题是指包含 “必须” “允许” “禁止” 的命题。
⑤ a.任何公民都应遵守宪法。(任何+都+道义模态算子)
b.未经同意,任何同学(都)不得离开教室。(双重否定)
c.未经许可,任何厂家(都)不得在电视上作广告。(双重否定)
⑤a中, “任何” 可以与 “都” 和道义模态算子连用构成合法语句。⑤b和⑤c中,在双重否定句中, “都” 可以出现也可以不出现,但是可以看出,限定词 “任何” 是在第一个否定算子的辖域内。因此, “都” 不必强制出现。从以上分析可以看出,除去道义命题外,限定词作为前置宾语必须得到 “都” 和否定算子的双重允准。
(三) “都” 与否定极性极小词的分布
与英语中极小词 “a+np” 平行的 “一量(np)” 和限定词类似,否定算子是通过否定某个范围的最小单位以达到对整个范围的否定。在大多数情况下 “一量(np)” 用在否定的语境中,且否定算子需在 “一量(np)” 之前。如⑥b。如果否定算子出现在 “一量(np)” 之后。否定算子需与 “都” 连用,如⑥d。
⑥ a.一滴水。(NPI)
b.天上没有一颗星星。(Neg+NPI)
c.★天上一颗星星都有。(NPI+都)
d.他一句话都没有说。(NPI+都+Neg)
e.★他一句话没有说。(NPI+Neg)
⑥a中,极小词可以单独作为短语用在肯定句,表示陈述极小词所表达的这一事实,一般情况下,极小词要在否定算子的辖域内,如⑥b。⑥d中,极小词作为前置宾语,需要与 “都” 和否定算子连用,而⑥c和⑥d表明,极小词作为前置宾语,只有 “都” 或只有否定算子的允准是不够的,可以看出,极小词和限定词的极性分布类似,都需要得到 “都” 和否定算子的双重允准。
(四) “都” 与否定极性副词的分布
否定极性副词广泛地存在于汉语中。例如,时间副词:从、从来、始终、迟迟;范围副词:概、一概、全然;语气副词:并、又、决、万、万万、千万、切、断、断断、断乎、压根儿、死、死活;程度副词:毫、丝毫。郑玉贵(2019)根据否定极性副词对否定语境的依赖程度不同对否定极性副词进行分类:从、毫、丝毫、断、断断、断乎、决、绝(表语气)、概、了(liao)、死、万、万万、并(表语气)14个为极强否定极性副词,只能在显性否定的语境中得到允准;又(表语气)、迟迟、千万、切4个为强否定极性副词,可以在显性的语境中或隐性的否定语境中得到允准。从来、根本、压根儿、死活、全然、始终、一概等7个为非严格否定极性副词,[4]这些副词对否定的语境依赖较弱,很多情况还可以用在肯定句,见表1。
显性否定是指带有否定词 “不” “没(有)” “别” 等否定词的否定表达;隐性否定是指不直接带有否定词的否定表达,其否定的含义隐含在肯定的表述中,如怀疑提防、妨碍、以免、避免等等。[4]在表1中,仅有个别副词能够与 “都” 连用,如极强否定极性副词 “丝毫” “死” ,强否定极性副词 “迟迟” “千万” ,弱否定极性副词 “从来” “根本” “压根儿” “死活” “全然” “始终” “一概” 。由于 “都” 作为语气副词与否定极性副词连用只起到加强语气的作用,仅选取个别副词作为分析,不影响研究结果。

表1 否定极性副词分类表
1.极强否定极性副词(丝毫)
⑦ a.★我们有丝毫的防御设施。(NPI)
b.他没有丝毫招架之力。(Neg+NPI)
c.★他丝毫都在意别人的看法。(NPI+都)
d.他丝毫都不在意别人的看法。(NPI+都+Neg)
e.他丝毫不在意别人的看法。(NPI+Neg)
⑦a和⑦c表明,极强否定极性副词 “丝毫” 只能用在否定的语境,⑦b可以看出,副词 “丝毫” 在否定算子的辖域内可以得到允准,但⑦d和⑦e可以看出, “都” 在 “NPI+都+Neg” 的结构中可以出现也可以不出现, “都” 作为语气副词,在当中只起到加强语气的作用。
2.强否定极性副词(迟迟)
⑧ a.★双边协定迟迟能签署。(NPI)
b.★李广没有迟迟用武之地。(Neg+NPI)
c.★李广迟迟都有用武之地。(NPI+都)
d.他迟迟都没有动笔。(NPI+都+Neg)
e.他迟迟没有动笔。(NPI+Neg)
在⑧中,选取 “迟迟” 作为例子,从⑧可以看出强否定极性副词也必须用在否定的语境中,⑧d和⑧e表明, “都” 在 “NPI+都 +Neg” 的结构中可以出现也可以不出现,原因是 “都” 作为语气副词,在当中只起到加强语气的作用。
3.弱否定极性副词(从来)
⑨ a.他从来就是一个正直善良的人。(NPI)
b.并非从来就有。(Neg+NPI)
c.我们老板从来都是一个说话算数的人。(NPI+都)
d.他从来都不惹事生非。(NPI+都+Neg)
e.他从来不惹事生非。(NPI+Neg)
弱否定极性副词也有很多,在此只选取 “从来” 作为代表。由于弱否定性极副词既可以用在肯定的语境又可以用在否定的语境, “都” 在 “NPI+都+Neg” 的结构中可以出现也可以不出现, “都” 同样作为语气副词,在语句中起到加强语气的作用。
整理以上 “都” 与否定极性项的分布如表2所示。
在表2中,限定词 “任何” 在肯定的语境中无法得到允准,但是在道义命题中, “任何” 可以得到 “都” 的单独允准,在双重否定的道义命题中, “都” 可以隐去。极小词 “一量(np)” 在否定算子之前,必须得到 “都” 和否定算子的双重允准;光杆疑问词 “什么” 在否定算子之前也必须得到 “都” 和否定算子的双重允准,但在疑问句中不需要得到 “都” 的允准;在严格否定极性副词中,极强和强否定极性副词 “丝毫” “迟迟” 等必须得到否定算子的允准,而 “都” 不必强制出现,弱否定极性副词 “从来” “根本” “死活” 等可以出现在肯定的语境中,也可以出现在否定的语境中。总的来看,汉语否定极性项中限定词、极小词、光杆疑问词与否定极性副词有所区别,前者的后面常常要紧跟名词np,而后者不需要紧跟名词np。因此, “都” 与上述两者连用所起的作用就不一样,与限定词、极小词、光杆疑问词连用的时候, “都” 作为全称量词,可以对限定词、极小词、光杆疑问词后的np起到全称量化的作用。 “都” 与极强否定极性副词、强否定极性副词、弱否定极性副词连用的时候,由于这些副词后并未紧跟名词np,此时, “都” 作为语气副词,用来帮助极性项加强语气。
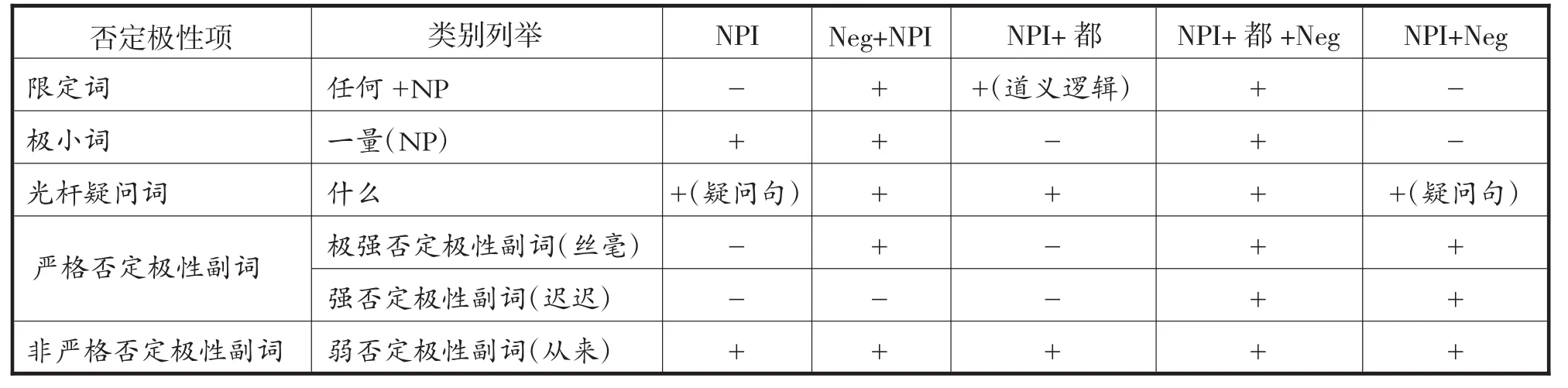
表2 “都” 与否定极性项的分布
四、 “都” 创造的向下蕴涵语境
拉杜索 (Ladusaw,1980) 提出了向下蕴涵(Downward Entailment)理论,向下蕴涵的定义如下:
∀X∀Y[X⊆Y→δ(Y)⊆δ(X)][5]
即:函数δ是向下蕴涵的,当且仅当对于每一个X,Y,如果X是Y的子集,那么δ(Y)是δ(X)的子集。向下蕴涵理论认为否定极性项与其所在语句的真值条件密不可分,向下蕴涵的函数F可以实现由集合到子集衍推,由此,拉杜索在语义层面运用逻辑蕴涵解释了否定极性项只能存在于向下单调的语境中。例如:
① a.Ann doesn’t eat any vegetables.→ b.Ann doesn’t eat any tomatoes.
②a.Ann eats tomatoes.→b.Ann eats vegetables.
其中[tomatoes]⊆[vegetables],集合[tomatoes]是集合[vegetables]的子集,或者说集合[vegetables]是集合[tomatoes]的超集;①a是否定句,当我们说Ann doesn’t eat any vegetables,可以推出 Ann doesn’t eat any tomatoes;反之则无效。可见,在否定句中从某集合到其子集的推理有效,否定算子创造向下蕴涵的语境,使得否定极性项any得到允准。②a是肯定句,当我们说Ann eats tomatoes,可以推出Ann eats vegetables,反之则无效。可见,在肯定句中从某集合到其超集的推理有效,否定极性项 “any” 在向上蕴涵的语境中不能出现。根据拉杜索的蕴涵理论, “every” 和 “no” 是向下蕴涵的,而 “some” 是向上蕴涵的,顺着拉杜索的思路,汉语 “都” 作为全称量词应该与 “every” 相似也是向下蕴涵的,只不过 “都” 的辖域在 “都” 的左侧。因此,否定极性项中的限定词 “任何” 和极小词需要否定算子和全称量化算子 “都” 的双重允准,就能用Ladusaw的蕴涵理论来解释了。
③ a.任何士兵都没有吃饭。
[米饭]⊆[饭]
b.任何士兵都没有吃米饭。
④ a.任何士兵都没有吃饭。
[男士兵]⊆[士兵]
b.任何男士兵都没有吃饭。
③中,集合[米饭]⊆集合[饭],当我们说 “任何士兵都没有吃饭” 时,可以推出 “任何士兵都没有吃米饭” ,此时,否定算子 “没有” 创造了向下蕴涵的语境。因此,③中,a到b的推理有效。在④中,集合[男士兵]⊆集合[士兵],当我们说 “任何士兵都没有吃饭” 时,可以推出 “任何男士兵都没有吃米饭” ,此时 “都” 也创造了向下蕴涵的语境。因此,可以看出,限定词 “任何” 既需要否定算子的管辖又需要有一个向下单调推理的语境。但限定词 “任何” 没有在否定算子的辖域内,而是在 “都” 的辖域内,此时,作为全称量化算子的 “都” 代替否定算子创造向下蕴涵的语境。
⑤ a.园中一朵花都没有。
[红花]⊆[花]
b.园中一朵红花都没有。
⑤中,否定算子 “没有” 右侧没有成分,没有办法对a进行单调向下推理,但在⑤中,集合[红花]⊆集合[花],当我们说 “园中一朵花都没有” 时,可以推出 “园中一朵红花都没有” ,此时, “都” 也创造了向下蕴涵的语境,并且 “一朵红花” 在 “都” 的辖域内。
⑥ a.什么人都没吃盘中的水果。
[苹果]⊆[水果]
b.什么人都没吃盘中的苹果。
⑦ a.什么人都没吃盘中的水果。
[男人]⊆[人]
b.什么男人都没吃盘中的水果。
⑥中,集合[苹果]⊆集合[水果],当我们说 “什么人都没吃盘中的水果” ,可以推出 “什么人都没吃盘中的苹果” ,此时,否定算子 “没” 创造了向下蕴涵的语境。因此,⑥中a到b的推理有效。⑦中集合[男人]⊆集合[人],当我们说 “什么人都没吃盘中的水果” 时,可以推出 “什么男人都没吃盘中的水果” ,当然也可以推出 “什么男人都没吃盘中的苹果” ,此时, “都” 也创造了向下蕴涵的语境,并且 “什么人” 在 “都” 的辖域内。因此⑦中,由a到b的推理有效。
⑧ a.他死活不同意。
b.他死活都不同意。
值得说明的是,否定极性副词既不需要否定算子的强制出现,也不需要 “都” 强制出现, “都” 也不作为全称量词创造向下蕴涵的语境,而是作为语气副词加强语气,在否定句中用于强调对象的含义。如 “都” 在⑧b中加强了副词的意义。
在拉杜索的蕴涵理论中,允准成分被形式化地看成是函项,被允准成分被形式化为函项的论元,这就为针对极性项的单调推理提供了思路,但拉杜索的理论也存在问题, “not” 分句内否定和句外否定,在句外否定中,其否定的辖域是整个句子,在句内否定中却不尽然,按照向下蕴涵理论,句内否定也可以创造向下蕴涵的语境,但句内否定并不能允准否定极性项any。如:
⑨ a.★Any teacher doesn’t love students.→
b.★Any teacher doesn’t love male students.
c.★任何老师不爱学生。→
d.★任何老师不爱男学生。
e.任何老师都不爱学生。→
f.任何男老师都不爱学生。
⑨a中,否定算子创造了向下蕴涵的语境,但 “any” 不在否定算子的辖域内。因此,⑨a不合语法。⑨c的情况与⑨a类似。在⑨c中,否定极性项并不在否定算子的辖域内,即使否定算子创造了向下单调的语境,也不能使得从c推出d有效。但与英语不同的是汉语可以加上 “都” 来允准否定极性项,如⑨e。⑨e的合法性在于 “任何老师” 在 “都” 的辖域内,且 “都” 创造了向下蕴涵的语境。因此,在⑨中,由e到f的推理有效。
五、小结
作为自然语言中的总括副词 “都” 与形式语言中的全称量词一样,都具有全称量化的逻辑性质。但与常见的全称量词不同, “都” 的管辖对象在其左边,要对其左边的np进行全称量化。在拉杜索的蕴涵理论中,全称量词可以创造向下蕴涵的语境,从而能够实现向下单调推理。因此, “都” 左边的np成分可以向下蕴涵,从而使得相对应的向下单调推理有效。限定词 “任何” 和极小词需要否定算子和全称量化算子 “都” 的双重允准也可以归结到 “都” 创造的向下蕴涵语境。形式语言来源于自然语言,过去的研究大多从数学那里获取研究题材,忽视了自然语言中真实存在的许多逻辑规律。自然语言中有无穷无尽的逻辑规律有待挖掘,对量词性质的研究扩充了 “逻辑有效” 的概念,借助量词所具有的单调性(monotonicity),一些自然语言推理能够获得直观上的解释。
注释
(1) “极性敏感” 是指某些词语对语境分布非常敏感,具有倾向于只在否定或肯定的语境中分布的特点。
(2)汉语否定极性极小词是最常见的否定强调手段,包括原型/名词极小词(一(量)+np)、副词极小词、习语极小词等,其中名词极小词是主要表现形式。
(3)符号 “★” 表示句子表达不合语法。
