基于应力–强度干涉模型的分离螺母可靠性分析
2023-01-10牛磊董海平赵象润李朝振严楠
牛磊,董海平,赵象润,李朝振,严楠
基于应力–强度干涉模型的分离螺母可靠性分析
牛磊1,董海平1,赵象润2,李朝振3,严楠1
(1.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081;2.辽宁北方华丰特种化工有限公司 火工品技术研究所,辽宁 抚顺 113003;3.中国电子科技集团公司光电研究院,天津 300308)
提出一种基于应力强度干涉模型的分离螺母的分离可靠性分析方法。首先,建立分离螺母机构分离动力学模型和极限状态函数。然后,在考虑工作载荷、几何尺寸和药剂燃烧参数等参数不确定性的基础上,建立分离螺母不同分离阶段的基于应力–强度干涉模型的可靠性模型。最后,对分离螺母进行可靠性和灵敏度分析,量化工作载荷、几何尺寸和火药燃烧参数对分离螺母机构分离可靠性的重要性排序。影响可靠性的主要参数依次为火药力、装药密度和预紧力。该方法能够准确描述不确定性因素对分离螺母分离过程可靠性的影响,提升分离螺母机构分离可靠性定量分析的精度和效率,可为分离螺母的精细化设计提供支撑。
分离螺母可靠性;应力–强度干涉模型;可靠性分析;灵敏度
航天火工分离装置是指利用火炸药燃烧或爆炸反应产生的高温高压气体或冲击波,实现卫星释放、级间和有效载荷分离、天线和太阳帆板展开、降落伞展开和释放等功能的火工装置的总称,包括爆炸螺栓、解锁螺栓、拔销器、切割器、分离螺母等。分离螺母具有连接能力强、解锁压力小和分离冲击小等优点,被广泛应用于航空航天的整流罩分离、火箭级间分离、卫星释放等诸多航天领域[1-4],是我国目前嫦娥系列月球探测器、载人航天器、小行星探测器等深空探测、天地往返飞行器等重大航天工程中飞行器级间分离、机构分离控制的一次性动力源装置,它在航天飞行任务中的作用性能及工作可靠性是否能满足预先规定的要求,直接关系着航天器飞行任务的成败。
近年来,为提高分离螺母的作用性能和可靠性,国内外学者利用有限元仿真技术对分离螺母的作用过程、设计影响因素、输出性能等开展了广泛的研究。文献[5]建立了分离螺母的有限元模型,采用有限元分析法对分离螺母机构的分离过程进行了模拟分析,可为分离螺母的设计提供参考。文献[6]模拟了分离螺母的动态冲击过程,得到了卫星与发射装置接口处的载荷曲线。这些分离螺母的仿真分析主要是从分离螺母的结构、材料及几何尺寸等因素对分离螺母的功能和性能进行了研究,尚未对分离螺母机构分离可靠性进行仿真分析研究,未考虑外部载荷、材料属性、结构尺寸、加工误差等不确定因素对分离螺母机构分离可靠性的影响。
分离螺母的作用过程一般包含主装药产生高温高压气体,推动内套筒和活塞的运动,使螺母瓣产生位移,直至分离解锁的实现。根据机械运动可靠性分析理论[7],这个运动过程可以采用应力–强度干涉模型来描述[8-10],推动内套筒、活塞和螺母瓣运动的推力可视为应力,阻止其运动的力(包括剪切销强度、摩擦力等)视为强度[11]。当应力大于强度时,表示能正常运动,分离螺母实现分离;反之,分离失败。外部载荷的变化、材料参数的分散性、结构尺寸的公差、工艺参数的散差等这些不确定性因素的影响会导致应力和强度的变化,而这些变化可直接影响分离螺母的作用过程是否正常,即影响其工作可靠性。通过应力–强度干涉模型可以反映材料参数、结构尺寸、工艺参数等不确定性对分离螺母工作可靠性的影响,因此本文拟采用应力–强度干涉模型对分离螺母的可靠性进行建模与分析。
本文首先建立了分离螺母分阶段作用过程动力学模型和极限状态函数,然后基于分离螺母不同分离阶段建立了基于应力–强度干涉模型的可靠性模型,最后进行了可靠性分析和灵敏度分析,量化给出了材料参数、结构尺寸、工艺参数等不确定性对分离螺母工作可靠性的影响。
1 某分离螺母基本结构及工作原理
低冲击分离螺母的主要结构包括壳体、内套筒、活塞、剪切销、螺母瓣、密封圈、端盖等部件,如图1所示。

图1 分离螺母结构
分离螺母的工作原理为:电爆管点火,火药燃烧生成的气体产物在容腔内形成压力,驱动内套筒运动,剪断剪切销,并运动到解除对螺母瓣的约束临界状态;当内套筒运动达到一定行程时,解除对螺母瓣的约束,螺母瓣在活塞的推动和螺栓预紧力的双重作用下开始径向扩张;当螺母瓣扩张到一定距离后,螺母瓣的螺牙与螺栓的螺牙脱离,解除螺母瓣对螺栓的约束,螺栓在预紧力的作用下飞出,完成分离过程。
2 分离螺母各阶段运动过程极限状态函数
将分离螺母的机构运动失效定义为容腔内输入压力后,受随机变量影响而使机构不能运动到规定设计位置的状态。因此,根据分离螺母机构运动规律,将分离螺母机构运动失效模式划分为:内套筒启动失效、内套筒运动失效、螺母瓣启动失效和螺母瓣运动失效。下面分别建立各阶段运动过程的极限状态函数。
2.1 建立内套筒启动极限状态函数
内套筒启动失效是指内套筒未能克服剪切销、密封圈以及螺母瓣的阻力导致不能启动,该阶段内套筒的受力模型如图2所示。
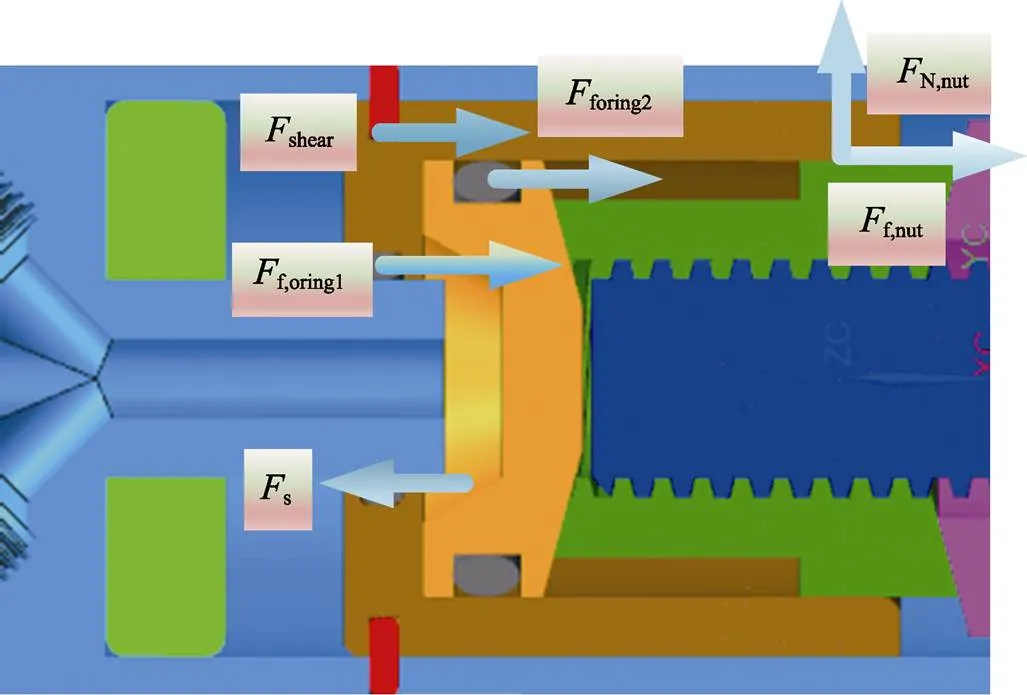
图2 内套筒启动阶段受力分析
因此,内套筒的启动的极限状态函数为:

式中:s为点火器输出压力,N;shear剪切销剪切力,N;f,oring密封圈摩擦力,N;f,nut为内套筒与螺母瓣之间的摩擦力,N。
根据文献[12],shear可按照式(2)进行计算:

所研究的分离螺母中有2个密封圈,分别安装在内套筒小内径和活塞外径处,密封圈参数见表1。根据文献[13],密封圈在气体压力作用下产生的摩擦力的计算公式为:

式中:选用O型密封圈材料为耐热材料氟橡胶,m为密封圈与内壁之间的摩擦系数;m为密封圈外径,mm;m为圆截面直径,mm;m为密封圈材料的弹性模量,MPa;为密封圈材料的泊松系数;为密封圈预压缩率,m为沟槽底部至外筒内壁的距离,mm。
表1 O型密封圈参数

Tab.1 Parameters of O-ring
对于密闭膛内高温高压燃气,在压力<600 MPa时,为[14]:

式中:为装药的火药力,kJ/kg;为装填密度,g·cm–3;为余容,dm3/kg。
s按照式(5)进行计算。

式中:(•)表示不同机构的受压面积,mm2;(•)表示不同机构。
根据内套筒启动的受力模型,螺母瓣与内套筒之间的摩擦力为:

式中:为活塞与螺母瓣的支撑角,(°);为螺母瓣与端盖之间的支撑角,(°);为螺母瓣的牙型半角,(°);pre为预紧力,N;nut-sle为内套筒与螺母瓣的摩擦系数。
在内套筒启动极限状态函数1中,经过工程分析,对分散小的参数可以视为固定参数;反之,可视为随机变量,也可称为不确定参数。在工程中,这些随机变量一般认为服从正态分布,设计尺寸为均值,标准差取为设计公差之差的1/6[15]。各参数的取值见表2。
表2 内套筒启动极限状态函数不确定参数

Tab.2 Uncertain parameters of inner sleeve starting limit state function
2.2 建立内套筒运动极限状态函数
内套筒运动失效是指内套筒的位移未能运动到解除对螺母瓣的约束临界状态。建立内套筒运动的极限状态函数为:

式中:(sle)为内套筒位移函数;unlock1为解除对螺母瓣的约束临界位移,根据设计尺寸可得unlock1为5 mm。此时,内套筒的运动到解除螺母瓣约束的位移表达式为:

式中:sle为内套筒的质量,kg;oring1为内套筒内径密封圈的质量,kg;1为内套筒启动到解除对螺母瓣约束的时间,经仿真分析得到1为4.19 ms[16]。
根据内套筒运动极限状态函数2,与前述类似考虑,内套筒运动的不确定性因素为:m1、m2、、、、pre、sle、、piston、,取值见表2。
2.3 建立螺母瓣启动极限状态函数
螺母瓣启动失效是指在燃气压力的推动下,螺母瓣未能克服与螺栓、活塞、端盖等机构之间的摩擦力,导致螺母瓣不能启动,该阶段螺母瓣受力模型如图3所示。
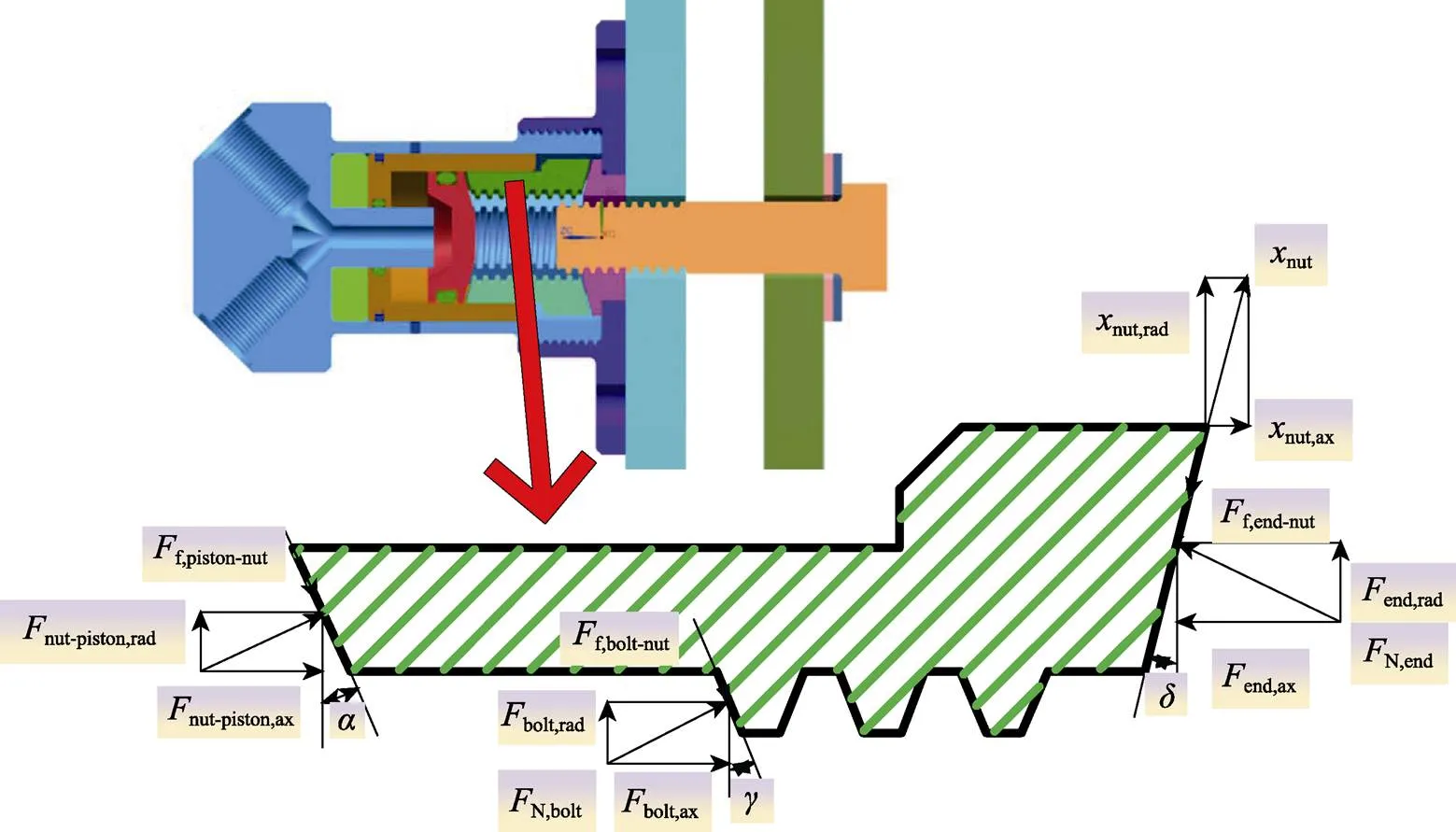
图3 螺母瓣启动阶段受力分析
根据螺母瓣启动的力学模型建立的极限状态函数为:
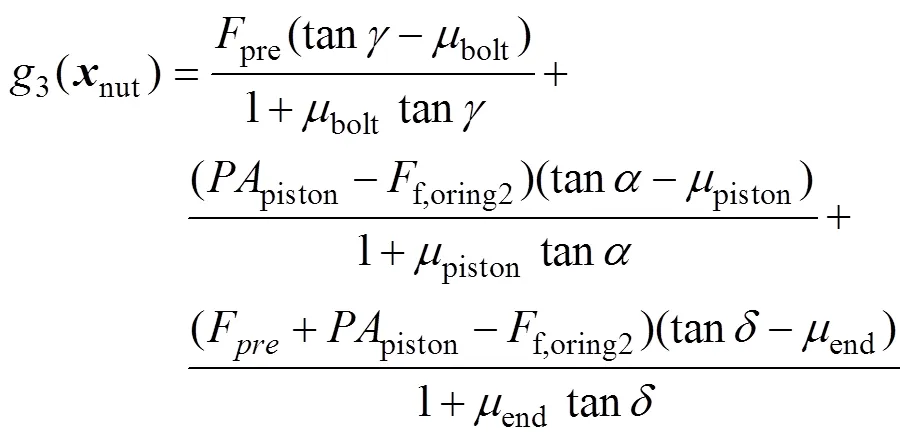
式中:bolt、piston、μend分别为螺母瓣与活塞、螺栓、端盖之间的摩擦系数。
根据极限状态函数3,给出螺母瓣启动的不确定性因素为:m2、、、、pre、、piston、,取值见表2。
2.4 建立螺母瓣运动极限状态函数
螺母瓣运动失效是指螺母瓣的径向约束解除后,螺母瓣的位移受到不确定因素的影响,未能解除对螺栓的约束。建立螺母瓣的运动的极限状态函数为:
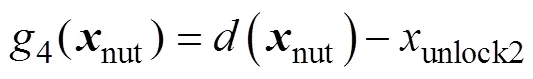
式中:(nut)为螺母瓣位移函数;unlock2为螺母瓣解除螺栓约束的有效位移,根据设计尺寸可得unlock2为2 mm。
该阶段活塞推动螺母瓣运动,由此该阶段螺母瓣轴向运动的位移表达式为:

式中:piston为活塞位移,mm;nut,ax为螺母瓣的轴向位移,mm;piston活塞的质量,kg;oring2为活塞外径的密封圈的质量,kg;2为螺母瓣启动到解除对螺栓的约束的时间,根据螺母瓣机构运动的仿真可得2为0.73 ms[16]。
根据极限状态函数4,给出螺母瓣运动的不确定性因素为:m2、、、、piston、,取值见表2。
3 基于应力–强度干涉模型的分离螺母可靠性分析模型
根据应力–强度干涉模型和机械可靠性理论[17],各阶段失效概率模型为:
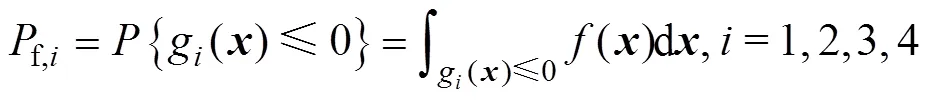
式中:f为失效概率;()是随机向量的联合概率密度函数。当g()>0,为分离螺母对应阶段工作正常;当g()<0,为分离螺母对应阶段工作失败;当g()=0,为极限状态。由于只有上述4个阶段工作都正常,分离螺母才工作正常,上述4个阶段的运动可靠度与分离螺母可靠度之间可视为串联关系,因此分离螺母的可靠性模型为:

基于式(13)的可靠度计算可采用蒙特卡洛模拟[18](Monte Carlo Simulation, MCS)方法求解。
针对灵敏度分析,本文将采用方差分析法[19]中的Kucherenko指标全局灵敏度分析方法进行灵敏度分析。Kucherenko指标是采用总方差定律分解输出方差定义灵敏度,就是将Sobol指标[20]扩展到输入变量的一种方法。Kucherenko指标总方差之和表达式为:
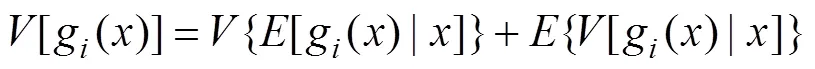
式中:(•)、(•)分别为方差与期望的算子。关于Kucherenko指标的全局灵敏度详细的求解过程参考文献[20]。
4 分离螺母机构运动可靠性分析结果
综上所述,通过分析分离螺母机构运动的失效模式,分别建立了分离螺母机构运动的极限状态函数,并采用MCS的方法[21-23]得到了分离螺母机构不同运动阶段的可靠度,内套筒启动、内套筒运动、螺母瓣启动和螺母瓣运动的可靠度分别为:0.999 997、0.999 979、0.999 481、0.999 996。
由于分离螺母的机构运动属于串联模型,采用串联的计算方法计算可靠度,见表3。
表3 分离螺母机构运动可靠性分析结果

Tab.3 Motion reliability analysis results of separation nut mechanism
基于方差全局灵敏度[24-26]分析评估了每个输入变量的敏感度指数,结果如图4所示。由图4可知,在内套筒启动阶段,影响可靠性的主要参数为、、pre、;内套筒运动阶段,影响可靠性的主要参数为、、pre;螺母瓣启动阶段,影响可靠性的主要参数为、、、、pre;螺母瓣运动阶段,影响可靠性的主要参数为、、piston。

图4 全局灵敏度分析结果
5 结语
本文提出了一种基于分离螺母机构分阶段运动动力学模型与应力–强度干涉模型结合的分离螺母可靠性分析方法。根据分离螺母机构运动过程,建立了机构分离分阶段运动动力学模型。选取工作载荷、几何尺寸和火药燃烧参数等随机变量,建立了分离螺母不同机构分离阶段基于应力–强度干涉模型的分离螺母可靠性模型。在整个分离螺母机构运动过程中,影响可靠性的主要参数为火药力、装药密度和预紧力pre,可通过调节这些设计值的大小和精度对产品的可靠性进行优化设计。
[1] 刘竹生, 王小军, 朱学昌. 航天火工装置[M]. 北京: 中国宇航出版社, 2012.
LIU Zhu-sheng, WANG Xiao-jun, ZHU Xue-chang. Space Pyrotechnic Device[M]. Beijing: China Aerospace Press, 2012.
[2] LEE J, HWANG D H, HAN J H. Study on Pyroshock Propagation through Plates with Joints and Washers[J]. Aerospace Science and Technology, 2018, 79: 441-458.
[3] 张醒, 张修科, 杨树彬, 等. 空间使用环境对火工装置性能的影响[J]. 火工品, 2013(5): 1-4.
ZHANG Xing, ZHANG Xiu-ke, YANG Shu-bin, et al. Influence of the Aerospace Environment on the Performance of Pyrotechnics Devices[J]. Initiators & Pyrotechnics, 2013(5): 1-4.
[4] DE BENEDETTI M, GAROFALO G, ZUMPANO M, et al. On the Damping Effect Due to Bolted Junctions in Space Structures Subjected to Pyro-Shock[J]. Acta Astronautica, 2007, 60(12): 947-956.
[5] ZHAO Hong-da, LIU Wei, DING Ji-feng, et al. Numerical Study on Separation Shock Characteristics of Pyrotechnic Separation Nuts[J]. Acta Astronautica, 2018, 151: 893-903.
[6] HAN D H, SUNG H G, JANG S G, et al. Parametric Analysis and Design Optimization of a Pyrotechnically Actuated Device[J]. International Journal of Aeronautical and Space Sciences, 2016, 17(3): 409-422.
[7] LIU Zi-yi, LUZhen-zhou, LING Chun-yan, et al. An Improved AK-MCS for Reliability Analysis by an Efficient and Simple Reduction Strategy of Candidate Sample Pool[J]. Structures, 2022, 35: 373-387.
[8] WEI Ning, LU Zhen-zhou. Sequential Optimization Method Based on the Adaptive Kriging Model for the Possibility-Based Design Optimization[J]. Aerospace Science and Technology, 2022, 130: 107939.
[9] WANG Jia-qi, LU Zhen-zhou, WANG Lu. A Novel Method for Estimating the Failure Possibility by Combining the Adaptive Kriging Model with the Markov Chain Simulation[J]. Aerospace Science and Technology, 2021, 119: 107205.
[10] YUN Wan-ying, LU Zhen-zhou, WANGLu, et al. Error-Based Stopping Criterion for the Combined Adaptive Kriging and Importance Sampling Method for Reliability Analysis[J]. Probabilistic Engineering Mechanics, 2021, 65: 103131.
[11] 荣吉利, 张涛, 宋乾强. 航天火工装置可靠性小子样分析评价技术[M]. 北京: 国防工业出版社, 2018.
RONG Ji-li, ZHANG Tao, SONG Qian-qiang. Small-Sample Analysis and Evaluation Technology of Aerospace Pyrotechnic Devices' Reliability[M]. Beijing: National Defense Industry Press, 2018.
[12] JIN Zhong-mou. Mechanics of Materials[M]. Beijing: Machinery Industry Press, 2009: 64-65.
[13] 徐辅仁. O形密封圈引起的摩擦力的计算[J]. 润滑与密封, 1989, 14(1): 32-34.
XU Fu-ren. Calculating Frictional Force Caused by O-Ring Seal[J]. Lubrication Engineering, 1989, 14(1): 32-34.
[14] 金志明. 枪炮内弹道学[M]. 北京: 北京理工大学出版社, 2004.
JIN Zhi-ming. The Ballistics of Interior Guns[M]. Beijing: Beijing Insititute of Technology Press, 2004.
[15] 杨帆. 电连接器锁紧分离机构可靠性设计方法的研究[D]. 杭州: 浙江理工大学, 2017.
YANG Fan. Reliability Design Method of the Locking Mechanism for Electrical Connectors[D]. Hangzhou: Zhejiang Sci-Tech University, 2017.
[16] NIU Lei, TU Hong-mao, DONG Hai-ping, et al. Separation Reliability Analysis for the Low-Shock Separation Nut with Mechanism Motion Failure Mode[J]. Aerospace, 2022, 9(3): 156.
[17] DITLEVSEN O, MADSEN H O. Structural Reliability Methods[M]. West Sussex: John Wiley & Sons Ltd, 2007.
[18] METROPOLIS N, ULAM S. The Monte Carlo Method[J]. Journal of the American Statistical Association, 1949, 44(247): 335-341.
[19] KUCHERENKO S, TARANTOLA S, ANNONI P. Estimation of Global Sensitivity Indices for Models with Dependent Variables[J]. Computer Physics Communications, 2012, 183(4): 937-946.
[20] SOBOL I M, TARANTOLAS, ANNONI P. Sensitivity Analysis for Non-Linear Mathematical Models[J]. Mathematical Modelling and Computational Experiment, 1993, 1: 407-414.
[21] ECHARD B, GAYTONN, LEMAIRE M. AK-MCS: An Active Learning Reliability Method Combining Kriging and Monte Carlo Simulation[J]. Structural Safety, 2011, 33(2): 145-154.
[22] ZHENG Pei-juan,WANG Chien-ming, ZONG Zhou-hong, et al. A New Active Learning Method Based on the Learning Function U of the AK-MCS Reliability Analysis Method[J]. Engineering Structures, 2017, 148: 185-194.
[23] CHEN Wei-dong,XU Chun-long, SHI Ya-qin, et al. A Hybrid Kriging-Based Reliability Method for Small Failure Probabilities[J]. Reliability Engineering & System Safety, 2019, 189: 31-41.
[24] SOBOL I M. Sensitivity Estimates for Nonlinear Mathematical Models[J]. Matematicheskoe Modelirovanie, 1990, 2: 112-118.
[25] HOMMA T, SALTELLI A. Importance Measures in Global Sensitivity Analysis of Nonlinear Models[J]. Reliability Engineering & System Safety, 1996, 52(1): 1-17.
[26] MARELLI S, LAMAS C, KONAKLI K, et al. UQLAB User Manual—Sensitivity Analysis[R]. Zurich: Q-Lab, 2019.
Reliability of Separation Nuts Based on Stress-Intensity Interference Model
NIU Lei1, DONG Hai-ping1,ZHAO Xiang-run2, LI Chao-zhen3,YAN Nan1
(1. State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China; 2. Institute of Pyrotechnics Technology, Liaoning North Huafeng Special Chemical Co., Ltd., Liaoning Fushun 113003, China;3. Academy of Opto-electronic, China Electronic Technology Group Corporation, Tianjin 300308, China)
The work aims to proposea method for reliability analysis of separation nuts based on stress-intensity interference model. Firstly, a separation dynamics model of the separation nut mechanism was established. Then, based on considering the uncertainty of parameters such as working load, geometric size and propellant combustion parameters, a reliability model based on stress-intensity interference model for different separation stages of the separation nuts was established. Finally, the reliability and sensitivity of the separation nuts were analyzed, and the importance of the working load, geometric size and gunpowder combustion parameters on the separation reliability of the separation nut mechanism was quantified. The most important parameters affecting the reliability were powder force, charge density and preload. The example shows that the method can accurately describe the effects of uncertain factors on the reliability of separation nuts during separation, improve the accuracy and efficiency of the quantitative analysis on the separation reliability of the separation nut mechanism, and provide support for fine design of separation nuts.
reliability of separation nuts; stress-intensity interference model; reliability analysis; sensitivity
V448
A
1672-9242(2022)12-0008-06
10.7643/ issn.1672-9242.2022.12.002
2022–11–25;
2022–12–05
2022-11-25;
2022-12-05
牛磊(1993—),男,博士研究生,主要研究方向为武器装备可靠性分析与寿命评估。
NIU Lei (1993-), Male, Doctoral candidate, Research focus: reliability analysis and life evaluation of weapon equipment.
董海平(1969—),男,博士,副教授,主要研究方向为武器装备可靠性技术。
DONG Hai-ping (1969-), Male, Doctor, Associate professor, Research focus: reliability technology of weapon equipment.
牛磊,董海平,赵象润, 等. 基于应力–强度干涉模型的分离螺母可靠性分析[J]. 装备环境工程, 2022, 19(12): 008-013.
NIU Lei, DONG Hai-ping, ZHAO Xiang-run, et al. Reliability of Separation Nuts Based on Stress-intensity Interference Model[J]. Equipment Environmental Engineering, 2022, 19(12): 008-013.
责任编辑:刘世忠
