复杂火工系统可靠性预计方法及软件研究

袁晓霞，付东晓，麻宏亮，张蕾，李芳，张蕊

专题——火工品安全性与可靠性

复杂火工系统可靠性预计方法及软件研究

袁晓霞，付东晓，麻宏亮，张蕾，李芳，张蕊

（陕西应用物理化学研究所 火工品安全性可靠性国防重点实验室，西安 710061）

解决在进行复杂系统的可靠性建模以及预计时，计算效率低、容易出错的问题。开展基于GO（Goal Oriented）法的复杂火工系统可靠性预计方法研究。建立不同种类火工组件的可靠性模型和算法，结合火工系统的GO图模型，对系统的可靠性进行预计以及定量分析。依据建立的可靠性模型以及算法，开发一套火工系统可靠性建模以及预计的软件，运用该软件对典型座椅弹射火工系统的可靠性进行预计，并且将软件计算结果与蒙特卡洛仿真方法得到的结果进行比较。软件计算结果与蒙特卡洛仿真方法所得结果的最大相对误差不超过0.004 8%。基于GO法的复杂火工系统可靠性预计方法是合理可行的，而且运用GO法开发的软件可以提高可靠性预计的计算效率，同时也为后续的 GO 图分析计算提供了技术支持。

复杂火工系统；可靠性；GO图模型；可靠性逻辑；蒙特卡洛法

火工系统是指由多个单元火工品或者火工装置组成，且能完成一定功能的组件集合，广泛应用于武器系统的点火、延期、传火以及控制系统，实现起爆、传爆、延期、推、拉、切割、抛撒以及姿态调整等功能。火工系统是武器系统中最敏感的部分，因此火工系统的安全性、可靠性在很大程度上影响和制约着整个武器系统的安全性和可靠性[1-3]。火工品可靠性一般要求很高，目前大多数火工品要求可靠度达到0.999，有的甚至要求达到0.999 9[4-5]。国内关于火工品的可靠性评估一般按照2个标准进行，即GJB 376—87《火工品可靠性评估方法》[6]及GJB/Z 377A—94《感度试验用数理统计方法》[7]。对于单元火工品的评估，一般采用计数法或者计量法，其中计数法适用于成败型实验，样本需求量大。另一种计量法适用于当火工品的某性能参数可以直接测量的情况，例如发火感度，样本观测值或正态变换后的值作正态检验后，利用正态统计容许限计算火工品的可靠度。对于火工品感度的可靠性，国内研究者开展了较多的工作[8-11]。然而计量法不能用于成败型产品的发火可靠度计算，因此不适用于研究高价值的火工系统。

可靠性预计是在产品设计阶段对系统可靠性进行估计的方法，主要是依据以往的设计经验、故障数据等基础信息，预测产品的可靠度，即预测产品在规定条件下完成固定功能的概率。可靠性预计可以找出设计方案中的薄弱环节，从而进行改进，提高系统的可靠性[12-13]。常用的系统可靠性模型和预计方法有可靠性框图法[14]以及故障树分析法[15-18]等。

对于复杂火工系统，由于其具有多时序性、多故障模式、多态性等特点，使得上文提到的可靠性预计方法存在明显的不足：

1）不易与火工系统实际的结构、工作原理和功能组成直接关联，以至于火工系统的设计改进无法直接反映在相应的可靠性模型中。

2）可靠性建模和分析过程复杂，受工程人员主观性的影响较大，工程设计人员难以掌握和检查。

3）运算繁杂，无法高效、快速地对复杂系统的可靠性进行定性以及定量分析。

随着可靠性研究的发展，研究者们开始采用蒙特卡罗法[19-21]、GO法（Goal Oriented Methodology）[22-24]以及贝叶斯法[25]等开展复杂系统的可靠性研究。其中，以GO法最为广泛，主要原因是GO法适用于多状态、多时序变化、动态性和复杂性高的系统。另一方面，基于GO法的可靠性建模与可靠性预计方法有极强的拓展性，其理论易于形成工程软件，便于工程人员操作。文中研究的复杂火工系统可靠性快速建模及预计软件是基于GO法的可靠性定量计算软件，可以快速、高效地对火工系统可靠性进行定量以及定性分析，该软件为火工系统可靠性建模和可靠性预计提供了一个新的技术途径。

1 火工系统可靠性预计方法研究

一般地，系统的可靠性预计可以通过3个步骤来完成，首先是建立系统可靠性模型，然后计算各个元器件和部件单元的可靠性指标，最后再根据可靠性模型和各个元部件的可靠性数据，计算系统的可靠性。上文已经提及GO法适用于多状态、多时序变化、动态性和复杂性高的系统可靠性分析，本文将基于GO法对复杂火工系统的可靠性进行分析，以下是基于GO法的复杂火工系统可靠性建模和可靠性预计方法研究流程。

1）根据火工系统的原理图，分析该系统的功能、结构组成、工作原理及其可靠性要求、成功判据和失效判据。

2）在火工系统结构组成和工作原理分析的基础上，分析该系统中包含的火工组件的类型、数量，每个火工组件的成功判据和失效判据，每个火工组件的输入和输出信号，以及每个火工组件输入和输出信号之间的逻辑关系。

3）进一步分析每个火工组件的状态数量和状态属性，火工组件输入和输出信号的状态数和状态属性，根据火工组件输入和输出信号之间的状态逻辑关系，建立各种类型火工组件的可靠性模型。

4）结合火工系统的原理图，建立整个火工系统的GO图模型。

5）基于GO图模型，输入各火工组件的状态属性参数，采用状态组合法或状态概率法按上述GO图模型进行概率计算，对火工系统的可靠性进行预计。

为了对复杂火工系统的可靠性进行预计，首先需要解剖系统所包含的元件或组件，并且理清复杂火工系统不同元件或组件之间的输入信号、元件或组件本身与输出信号之间的作用关系、作用时序规律和可靠性逻辑关系，并推导出相应的元件或组件的输入信号、元件或组件本身和输出信号之间的状态概率计算模型。典型的座椅弹射的火工系统由飞靶接收器、飞靶作动器以及多个入出的传爆组件等火工元件和组件组成，下面举例说明复杂火工系统中飞靶接收器组件、2入2出分路器组件的功能及可靠性逻辑计算方法。

1.1 飞靶接收器组件可靠性计算方法

飞靶接收器组件有1个输入信号和1个输出信号，当输入信号处于正常状态以及该组件也处于正常状态时，输出信号处于正常状态；当输入信号或该组件处于失效状态时，输出处于失效状态。飞靶接收器的符号如图1所示，R为输入信号，S为输出信号，FBJS为飞靶接收器组件的符号。该组件的输入信号、组件本身与输出信号的状态之间的逻辑关系见表1。

图1 飞靶接收器组件符号示意图

表1 飞靶接收器组件间的状态逻辑关系

Tab.1 State logic relation of flying target receiver components

注：1 表示正常状态；2表示失效状态。

根据表1飞靶接收器的可靠性逻辑规律，可以建立如下的串联可靠性模型：

因此，飞靶接收器组件的输入信号、组件本身与输出信号之间的状态概率或可靠度计算模型为：

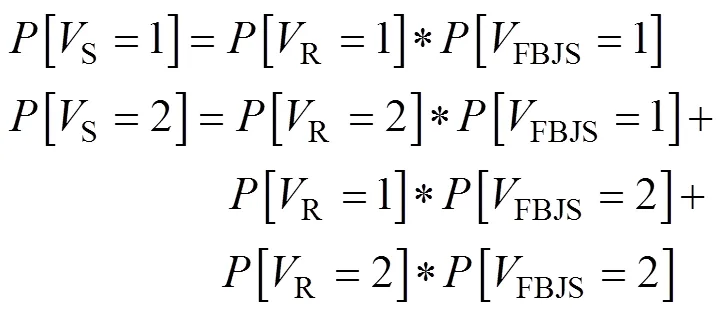
1.2 2入2出分路器组件可靠性计算方法

2入2出分路器有2个输入信号和2个输出信号，当2个输入信号中只要有1个处于正常状态，以及该组件本身也处于正常状态时，2个输出信号都处于正常状态。当2个输入信号都处于失效状态，或该组件本身处于失效状态时，2个输出信号处于失效状态。2入2出分路器组件的符号如图2所示，R1、R2为输入信号，S1、S2为输出信号，FLQ22为2入2出分路器组件的符号。2入2出分路器组件的输入信号、组件本身与输出信号的状态之间的逻辑关系见表2。

根据2入2出分路器组件的可靠性逻辑规律，可以建立如下的并联可靠性模型：

因此，2入2出分路器组件的输入信号、组件本身与输出信号之间的状态概率或可靠度计算模型为：

表2 2入2出分路器组件间的状态逻辑关系表

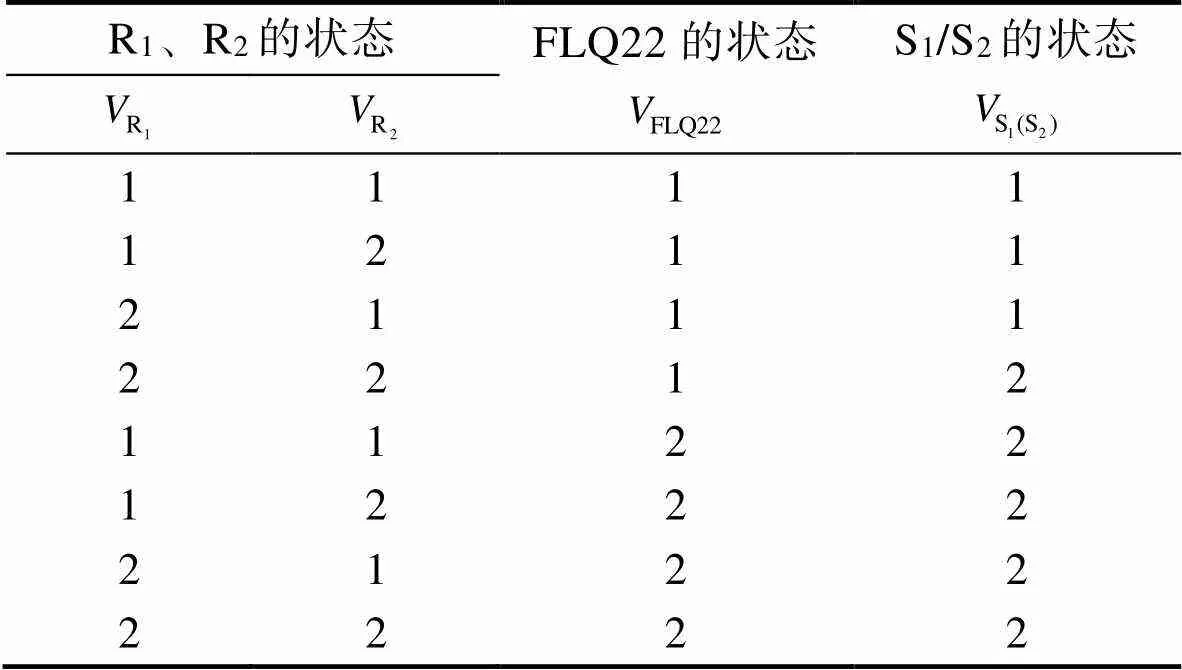
Tab.2 State logic relation of 2 in 2 out splitter components

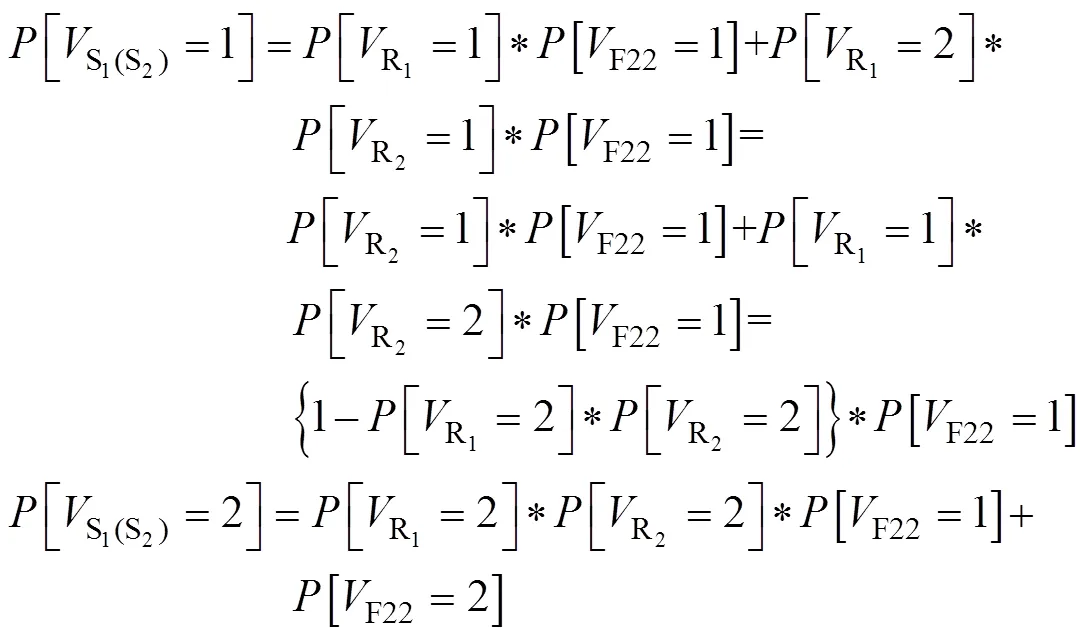
复杂火工系统其他组件的可靠性计算方法同上类推，运用以上可靠性计算方法，按顺序从左到右计算GO图模型所有信号（包括中间信号和输出信号）的状态概率，可以进行火工系统可靠性的定性分析和定量分析。

2 火工系统可靠性预计GO软件研究

基于建立的火工系统GO图模型，以及进行概率运算的过程，开发成软件，通过软件快速进行火工系统的可靠性建模和可靠性自适应计算，为火工系统快速进行可靠性建模和可靠性预计服务。

2.1 软件总体设计

本软件主要采用GO法对复杂火工系统进行可靠性预计，具体是指根据火工系统原理图，用户能够对火工系统中的每个元件、组件（包括连接各个元件之间的导爆索），直接在软件中选择对应的元件符号，通过软件提供的画图工具，采用拖拽的方式，在界面屏幕上画出与火工系统原理图对应的GO图模型。根据GO图模型，利用各个元件符号输入信号、元件符号本身以及输出信号之间的状态概率计算模型，从GO图左侧开始计算，按顺序从左到右计算GO图模型所有信号（包括中间信号和输出信号）的状态概率，进行火工系统可靠性分析。

本软件由3个模块构成，即火工系统元件模型库模块、火工系统GO图建模模块以及火工系统可靠性预计模块。3个模块相互配合，共同完成可靠性预计的任务。火工系统元件模型库负责全局处理功能与基础设置功能，包括元件视图设定、状态概率等参数设定等，利用图片形式显示元件符号，可显示元件符号各种属性信息和与元件相关的参数及数据，在本软件中的火工系统元件主要包含传爆组件、与门、或门、程序控制器、优先控制器、延时器、机械起爆器、切割控制器、分路器、单向传爆控制器、手柄、并路器、传爆接头、飞靶等；输入的数据为正常状态的概率或可靠度，数据类型为浮点数，取值在[0,1]，超出范围判为无效。火工系统GO图建模负责完成系统的可靠性图模型建立，通过本软件的画图工具，采用拖拽的方式，在界面屏幕上画出与火工系统原理图对应的GO图模型，为火工系统可靠性预计提供图形化模型。火工系统可靠性预计模块总体上说通过GO图模块各节点状态概率数值，按GO图顺序从左到右计算模型所有信号（包括中间信号和输出信号）的状态概率，软件总体框架如图3所示。

图3 软件总体框架

2.2 GO图模型建立

GO图模型的建立过程如下：选用工具中的鼠标工具，拖拽节点区中的元件到GO图模型区，进行模型的构造，绘制与火工系统原理图对应的GO图模型，并设置GO图模型对应的参数和所有元件类型的有效状态概率值，如图4所示。当GO图模型以及相关参数设置完成后，就可以点击功能菜单中的执行来进行计算了，软件会自动计算出系统的可靠性，并在GO图模型区域上显示出来。

2.3 软件验证及样例计算

以某型战机座椅弹射的火工系统为例，它是由飞靶接收器、飞靶作动器、多个入出的传爆组件、单向传爆控制器、程序控制器、多个具有不同延迟时间的延时器、舱外抛放手柄、舱内抛放手柄、烟火开关、开盖信号反馈器等火工元件和组件组成，输入信号为多路冲击波信号，输出信号为按照控制要求输出的冲击波信号，系统的主要功能是实现舱盖的切割与抛撒，随后按照一定的时序对各乘客弹射座椅发出弹射指令，该系统的可靠度要求为99.5%（置信度95%）。按照某复杂火工系统原理图，采用软件拖拽节点区中的元件，绘制的GO图建模如图5所示。

座椅弹射火工系统中各单元组件的可靠性数据见表3，按照GO软件的可靠性预计流程，依此建立模型元件库，输入各组件的可靠性数据，并结合建立的GO图模型，从而计算系统的可靠性。通过GO软件可以得到该火工系统工况1的可靠度为0.999 865，工况2的可靠度为0.999 849。为了验证本文中所采用GO法对系统可靠性预算的正确合理性，对于该座椅弹射救生火工系统，采用蒙特卡洛方法对系统可靠性进行预计。蒙特卡洛方法的原理是利用模拟抽样代替真实抽样，系统中每个元件抽取个1、0随机数，这些所抽取的随机数服从二项式分布（其中1出现的概率为该元件可靠性的值），这样就可以组成套系统。随后根据系统元件之间的逻辑关系，运用仿真计算得到这套系统最终实现功能的数量，则该系统的可靠性预计值为/。座椅弹射火工系统采用蒙特卡洛仿真的过程中，设定抽样数量=10 000 000，系统重复100次，计算结果见表4。将2种方法得到的系统可靠性预计值进行对比，得出2种结果的最大相对误差为0.004 8%。结果表明，本软件可用于对复杂火工系统的可靠性预计。

图4 GO图模型示例

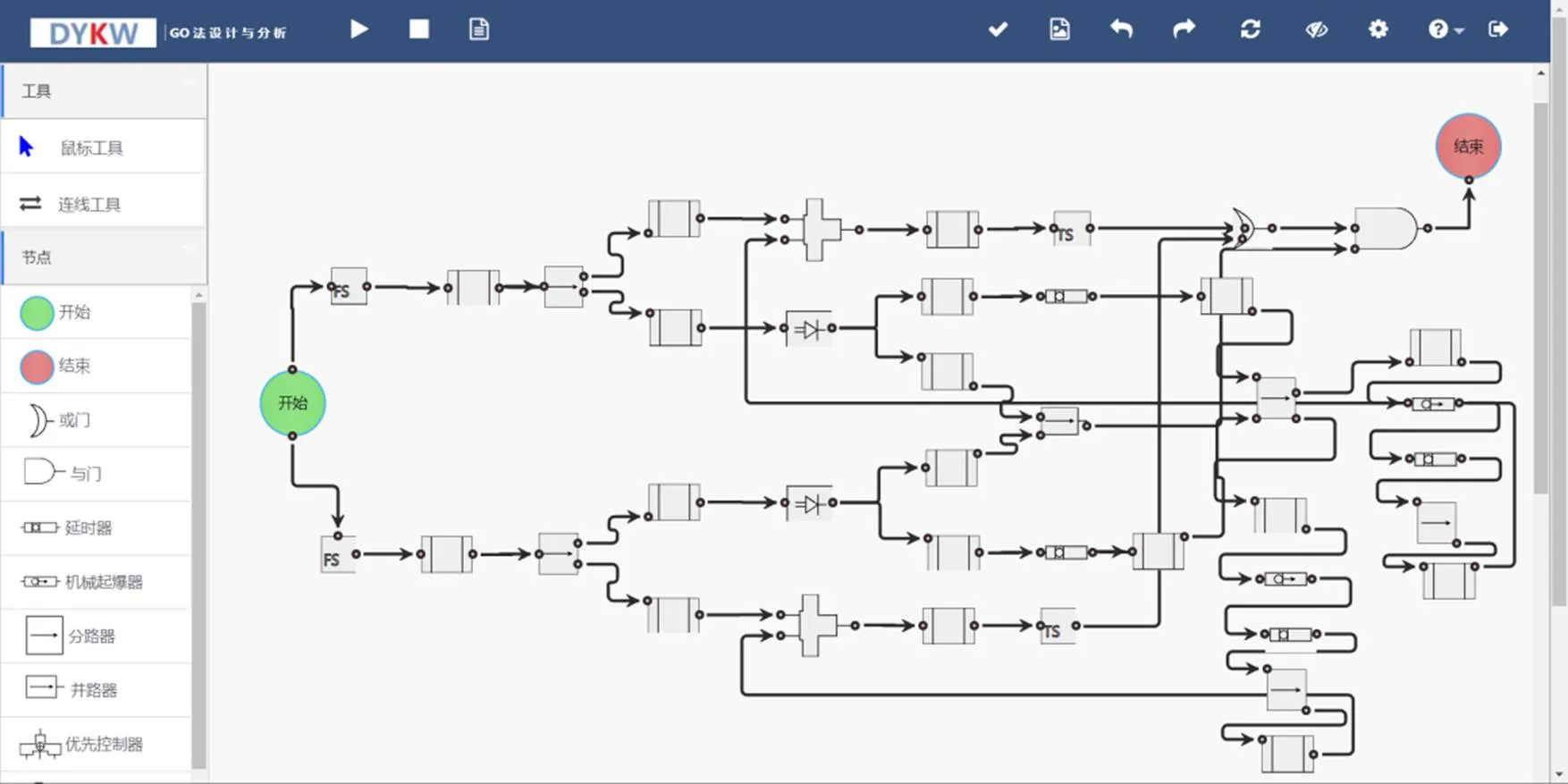
图5 某火工系统GO图建模界面

表3 某复杂火工系统中元件的可靠度

Tab.3 Reliability of components in a complex pyrotechnic system

表4 软件计算结果与蒙特卡洛方法计算结果对比

Tab.4 Comparison of software calculation results with Monte Carlo method

3 结语

本文开展了基于GO法的复杂火工系统可靠性预计方法及软件研究，建立了不同种类火工组件的可靠性模型和算法，结合火工系统的GO图模型，对火工系统的可靠性进行预计以及定量分析，并且依据该可靠性模型以及算法，开发了一套火工系统可靠性建模以及预计的软件。运用该软件对典型座椅弹射火工系统的可靠性进行预计，并且把计算结果与蒙特卡洛仿真方法得到的结果进行了比较，最大相对误差在一定的范围内，表明基于GO法的复杂火工系统可靠性预计方法及软件是合理可行的。基于GO法的可靠性预计方法解决了复杂系统可靠性计算繁琐且易出错等问题，运用该软件可以较快速找出设计方案中的薄弱环节，从而提出改进措施。例如，当系统中增加或者减少元件，或者某一元件的类型或可靠度值发生变化时，可以快速地利用本软件调整火工系统的可靠性定量分析，提供可靠性定量分析结果，为判断方案修改的合理性提供依据，提高方案设计和优化的效率。

[1] 王凯民. 火工品工程[M]. 北京: 国防工业出版社, 2014.

WANG Kai-min. Pyroengineering[M]. Beijing: National Defense Industry Press, 2014.

[2] 徐振相, 秦士嘉. 火工品可靠性技术[M]. 北京: 兵器工业出版社, 1996.

XU Zhen-xiang, QIN Shi-jia. Reliability Technology of Pyrotechnics[M]. Beijing: The Publishing House of Ordnance Industry, 1996.

[3] 王凯民, 温玉全. 军用火工品设计技术[M]. 北京: 国防工业出版社, 2006.

WANG Kai-min, WEN Yu-quan. Design of Initiators and Pyrotechnics for Weapon Systems[M]. Beijing: National Defense Industry Press, 2006.

[4] 张强. 火工品可靠性评定方法的分析与研究[J]. 舰船科学技术, 2010, 32(5): 92-94.

ZHANG Qiang. Analysis and Study on Reliability Assessment Method of Initiating Devices[J]. Ship Science and Technology, 2010, 32(5): 92-94.

[5] 周美林. 高价值火工品可靠性评估方法研究[D]. 北京: 北京理工大学, 2005.

ZHOU Mei-lin. Research on Reliability Evaluation Method of High Value Pyrotechnics[D]. Beijing: Beijing Institute of Technology, 2005.

[6] GJB 376—87, 火工品可靠性评估方法[S].

GJB 376—87, Methods for Reliability Assessment of Pyrotechnics[S].

[7] GJB/Z 377A—94, 感度试验用数理统计方法[S].

GJB/Z 377A—94, Mathematical Statistics Method for Sensitivity Test[S].

[8] 付东晓, 张蕊, 李芳, 等. 两种感度试验方法在不同初始试验参数条件下的适用性分析[J]. 测试技术学报, 2008, 22(6) : 83-87.

FU Dong-xiao, ZHANG Rui, LI Fang, et al. Applicability Analysis of Two sensitivity Test Methods under Different Initial Test Parameters[J]. Journal of Measurement Technology, 2008, 22(6): 83-87.

[9] 付东晓, 张蕊, 李芳, 等. 不同先验信息下D-优化法的估值精度及其适用性[J]. 含能材料, 2009, 17(3): 339-343.

FU Dong-xiao, ZHANG Rui, LI Fang, et al. Estimation and Its Applicability of D-Optimality-Based Sensitivity Test under Different Prior Information[J]. Chinese Journal of Energetic Materials, 2009, 17(3): 339-343.

[10] 温玉全, 张利敏, 洪东跑. 基于感度的火工品发火可靠性试验数据分析[J]. 兵工学报, 2010, 31(11): 1498-1501.

WEN Yu-quan, ZHANG Li-min, HONG Dong-pao. Analy­sis on Reliability for Explosive Initiator Based on Sensi­tivity[J]. Acta Armamentarii, 2010, 31(11): 1498-1501.

[11] 洪东跑, 王英华, 管飞, 等. 基于广义线性模型的火工品可靠性数据分析[J]. 含能材料, 2015, 23(3): 270-274.

HONG Dong-pao, WANG Ying-hua, GUAN Fei, et al. Reliability Analysis for Explosive Initiator Based on Generalized Linear Models[J]. Chinese Journal of Energetic Materials, 2015, 23(3): 270-274.

[12] 张根保, 徐付伟, 冉琰, 等. 机械结构相似度评价及可靠性预计研究[J]. 工程设计学报, 2017, 24(3): 264-272.

ZHANG Gen-bao, XU Fu-wei, RAN Yan, et al. Research on Similarity Evaluation and Reliability Prediction of Mechanical Structure[J]. Chinese Journal of Engineering Design, 2017, 24(3): 264-272.

[13] 潘广泽, 张铮, 罗琴, 等. 基于维纳过程和蒙特卡洛法的多元性能退化产品可靠性评估[J]. 环境技术, 2019, 37(S2): 107-111.

PAN Guang-ze, ZHANG Zheng, LUO Qin, et al. Reliability Evaluation of Multivariate Performance Degradation Products Based on Wiener Process and Monte Carlo Method[J]. Environmental Technology, 2019, 37(S2): 107-111.

[14] KIM M C. Reliability Block Diagram with General Gates and Its Application to System Reliability Analysis[J]. Annals of Nuclear Energy, 2011, 38(11): 2456- 2461.

[15] LEE W S, GROSH D L, TILLMAN F A, et al. Fault Tree Analysis, Methods, and Applications %DF%9D a Review[J]. IEEE Transactions on Reliability, 1985, 34(3): 194-203.

[16] 仝振亚, 王建文, 李便花, 等. 某火工品作用失效案例分析[J]. 兵工自动化, 2020, 39(1): 74-76.

TONG Zhen-ya, WANG Jian-wen, LI Bian-hua, et al. Case Analysis of Action Failure of a Firework[J]. Ordnance Industry Automation, 2020, 39(1): 74-76.

[17] 蒋敏荣. 火工品失效的量化分析方法[D]. 北京: 北京理工大学, 2003.

JIANG Min-rong. Quantitative Analysis Method of Pyrotechnics Failure[D]. Beijing: Beijing Institute of Technology, 2003.

[18] 张涛, 孙洁, 常英珂, 等. 某型拔销器功能失效分析[J]. 火工品, 2021(3): 16-19.

ZHANG Tao, SUN Jie, CHANG Ying-ke, et al. Analysis of Function Failure of some Pin Puller[J]. Initiators ＆ Pyrotechnics, 2021(3): 16-19.

[19] METROPOLIS N, ULAM S. The Monte Carlo Method[J]. Journal of the American Statistical Association, 1949, 44(247): 335-341.

[20] 付东晓, 张国兴, 张蕊, 等. 基于蒙特卡罗的复杂火工系统可靠性预计精度研究[J]. 火工品, 2019(5): 29-32.

FU Dong-xiao, ZHANG Guo-xing, ZHANG Rui, et al. Research on Reliability Prediction Accuracy of Complex Initiators System Based on Monte Carlo[J]. Initiators & Pyrotechnics, 2019(5): 29-32.

[21] 刘洋, 王佳, 江泳, 等. 基于故障树-蒙特卡洛的输电可靠性设计[J]. 电子设计工程, 2022, 30(6): 95-99.

LIU Yang, WANG Jia, JIANG Yong, et al. Transmission Reliability Design Based on Fault Tree-Monte Carlo[J]. Electronic Design Engineering, 2022, 30(6): 95-99.

[22] 沈祖培, 黄祥瑞. GO法原理及应用: 一种系统可靠性分析方法[M]. 北京: 清华大学出版社, 2004.

SHEN Zu-pei, HUANG Xiang-rui. Principle Application of GO Methodology[M]. Beijing: Tsinghua University Press, 2004.

[23] 王海朋, 段富海, 江秀红. 基于模糊GO法的惯性导航系统可靠性研究[J]. 大连理工大学学报, 2018, 58(3): 285-292.

WANG Hai-peng, DUAN Fu-hai, JIANG Xiu-hong. Research on Reliability of Inertial Navigation System Based on Fuzzy GO Methodology[J]. Journal of Dalian University of Technology, 2018, 58(3): 285-292.

[24] 金霞, 段富海. 基于GO法的电动静液作动器可靠性分析[J]. 大连理工大学学报, 2013, 53(6): 846-850.

JIN Xia, DUAN Fu-hai. Reliability Analysis of Electro Hydrostatic Actuator Based on GO Methodology[J]. Journal of Dalian University of Technology, 2013, 53(6): 846-850.

[25] LANGSETH H. Bayesian Networks in Reliability[J]. Reliability Engineering & System Safety, 2007, 92(1): 92-108.

Method and Software of Reliability Prediction for Complex Pyrotechnic System

YUAN Xiao-xia, FU Dong-xiao, MA Hong-liang, ZHANG Lei, LI Fang, ZHANG Rui

(Science and Technology on Applied Physical and Chemistry Laboratory, Shaanxi Applied Physics and Chemistry Research Institute, Xi'an 710061, China)

The work aims to solve the problems such as low computational efficiency and error-prone in reliability modeling and prediction of complex system. In this work, the method of reliability prediction for complex pyrotechnic system was analyzed based on the GO (Goal Oriented) method. The reliability model and algorithm of different kinds of pyrotechnics components were established. Combining with the GO diagram model of the system, the reliability of the system was predicted and quantitatively analyzed. Based on the reliability model and algorithm, the reliability prediction software of the pyrotechnic system was developed. The software was used to predict the reliability of a typical seat ejection pyrotechnic system, and the calculated results were compared with those obtained by the Monte-Carlo simulation method, and the maximum relative error was not more than 0.004 8%. It is concluded that the reliability prediction method based on the GO method is reasonable and feasible. Moreover, the reliability prediction software developed with the GO method can improve the computational efficiency and provide technical support for the subsequent GO diagram analysis and calculation.

complex pyrotechnic system; reliability; GO graph model; logic of reliability; Monte-Carlo method

TJ450

A

1672-9242(2022)12-0001-07

10.7643/ issn.1672-9242.2022.12.001

2022–11–25；

2022–12–05

2022-11-25；

2022-12-05

袁晓霞（1990—），女，博士，工程师，主要研究方向为火工品的安全性和可靠性。

YUAN Xiao-xia (1990-), Female, Doctor, Engineer, Research focus: safety and reliability of initiators & pyrotechnics.

付东晓（1981—），男，硕士，研究员，主要研究方向为火工品的安全性和可靠性。

FU Dong-xiao (1981-), Male, Doctor, Researcher, Research focus: safety and reliability of initiators & pyrotechnics.

袁晓霞, 付东晓, 麻宏亮, 等. 复杂火工系统可靠性预计方法及软件研究[J]. 装备环境工程, 2022, 19(12): 001-007.

YUAN Xiao-xia, FU Dong-xiao, MA Hong-liang, et al. Method and Software of Reliability Prediction for Complex Pyrotechnic system[J]. Equipment Environmental Engineering, 2022, 19(12): 001-007.

责任编辑：刘世忠