谐振开关电容变换器磁集成电感设计
2023-01-10李紫薇吴学智祁静静续文政
李紫薇 吴学智 王 静 祁静静 荆 龙 续文政
谐振开关电容变换器磁集成电感设计
李紫薇1吴学智1王 静2祁静静1荆 龙1续文政1
(1. 北京交通大学国家能源主动配电网技术研发中心 北京 100044 2. 深圳供电局有限公司 深圳 518001)
谐振开关电容变换器(SCC)因可实现零电流开关、减小开关损耗和提高功率密度而广泛应用于数据中心、电动汽车等高功率密度和增益比场合,电感元件作为其重要组成部分是影响变换器提高性能的关键因素。为解决变换器前后级谐振电流不等而导致的解耦困难问题,该文设计一种中柱不开气隙的解耦磁集成电感。在研究电路工作原理的基础上,通过对偶分析法分析并与耦合磁集成相比得出,中柱不开气隙的解耦磁集成方法电感耦合度更高、且能够实现两级解耦。变换器谐振参数不对称会导致前后级谐振周期不一致,该文采用完全对称绕组以降低绕组对磁性参数的影响,保证多个电感参数的一致性。最后制作实验样机,验证了所设计的谐振SCC磁集成电感的合理性和有效性。
耦合电感 解耦磁集成 完全对称绕组 谐振开关电容变换器
0 引言
开关电容变换器拓扑中只包含电容和开关器件,因此可大大减小变换器体积,适用于数据中心、电动汽车等对效率和功率密度要求较高的场合[1-3]。然而开关电容变换器在电容连接状态切换时会造成电流尖峰,谐振开关电容变换器(Switched Capacitor Converter, SCC)通过引入谐振电感实现功率器件软开关特性,可以抑制电流尖峰,在实现提高功率密度、提高效率等方面更具有优势[4-5]。文献[6]介绍了一种采用纵向级联设计的可实现宽降压比的谐振SCC,该变换器通过对占空比的调控能实现不同电压增益。
目前对高效率高功率密度变换器进行磁集成设计已成为研究热点[7-9]。对于谐振SCC而言,更多的研究集中在结构优化和控制策略上,目前对该变换器电感元件进行磁集成设计尚不成熟[10-11]。然而,电感元件作为谐振SCC中重要组成部分,是影响变换器在质量和体积上优化的关键因素。为实现谐振SCC前后谐振周期相同,需要保证电感参数的一致性。采用磁集成耦合电感方法,可以用单一的磁性元件实现多个元件的功能,更有利于降低磁性元件体积、减小电感电流纹波和磁性元件损耗、解决参数不一致的问题[12-14]。电感磁集成可分为耦合磁集成和解耦磁集成。文献[15]对交错并联多相变换器电感的不同集成方法进行了详细的分析和介绍,对不同磁通流向的工况进行了磁路分析及仿真,特别是对损耗、尺寸和耦合等问题进行了讨论。文献[16]对四相非对称耦合电感进行设计,根据占空比、电流纹波和响应速度对电感耦合系数和对称度进行设计。该方法对于多相耦合电感设计难度较大,不容易实现多相之间的完全对称,耦合电感彼此之间互相干扰。文献[17]采用抵消耦合作用集成方法,针对双频变换器将两个不同频率的电感集成在一起,减小了磁性元件的体积和质量,降低了开关损耗,并提高了变换器功率密度。
本文通过对谐振SCC工作原理的分析和电感电流时域表达式的推导,得出变换器存在前后级谐振电感电流不等的问题。目前磁集成研究大都是针对电感元件数量较少的变换器拓扑,且各电感工作电流相同。由于本文所研究的谐振SCC前后级电流不同而导致磁通不能完全抵消,为避免产生磁通叠加后过大的问题,本文选择中柱不开气隙的解耦磁集成方法。本文对耦合磁集成和解耦磁集成方法进行对偶变换分析,可知解耦磁集成方法的耦合系数更高,且能够实现两级解耦。谐振SCC变换器电感元件众多,且设计时需要保持前后谐振周期一致,采用独立电感不易实现。为解决此问题,本文采用完全对称绕组设计磁集成电感。最后制作了实验样机,通过实验验证了所设计磁集成电感方法的合理性和有效性。
1 谐振开关电容变换器拓扑分析
图1为谐振开关电容变换器拓扑,可以通过控制各开关管导通关断来切换工作状态。谐振开关电容变换器工作在互补模式时存在两种模态,各模态电流流向如图2所示。图3为互补模式下的驱动脉冲和主要电流电压波形。图中,i、o为输入和输出侧电压,1、2、3、4为谐振电容,1、2、3、4为谐振电感,S1、S2、S3、SD1、SD12、SD2、SD3、SD34、SD4、SDa、SDb、SDc、SDd为开关管。

图1 谐振开关电容变换器拓扑

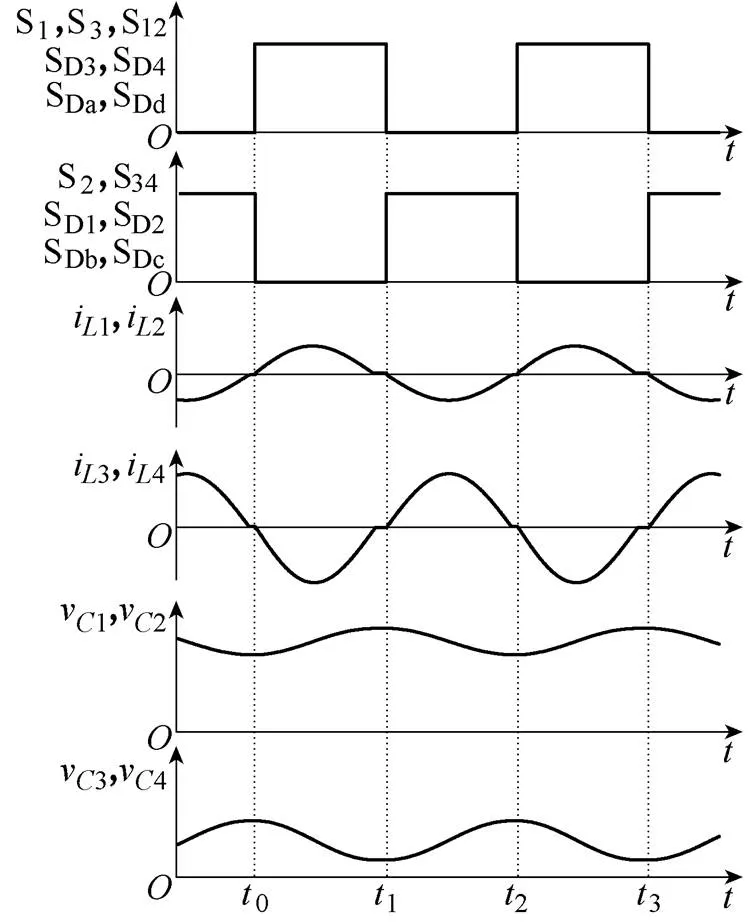
图3 驱动脉冲和主要电流电压波形
当变换器工作于0~1时,其电路状态如图2a所示。前级电感1和2处于串联状态,与电容正向谐振;后级电感3和4处于并联状态,与电容反向谐振,此时S1、S3、SD12、SD3、SD4、SDa、SDd实现零电流软开关(Zero Current Switching, ZCS)。令1=2=3=4=o,1=2=3=4=o,根据电路可得

式中,i1、i3分别为流过1、3的电流;v1、v3分别为1、3两端的电压。
当变换器工作于1~2时,其电路状态如图2b所示。前级电感1和2处于并联状态,与电容反向谐振;后级电感3和4处于串联状态,与电容正向谐振,此时S2、SD1、SD2、SD34、SDb、SDc实现ZCS。由于变换器各电感电容参数相同,则可得
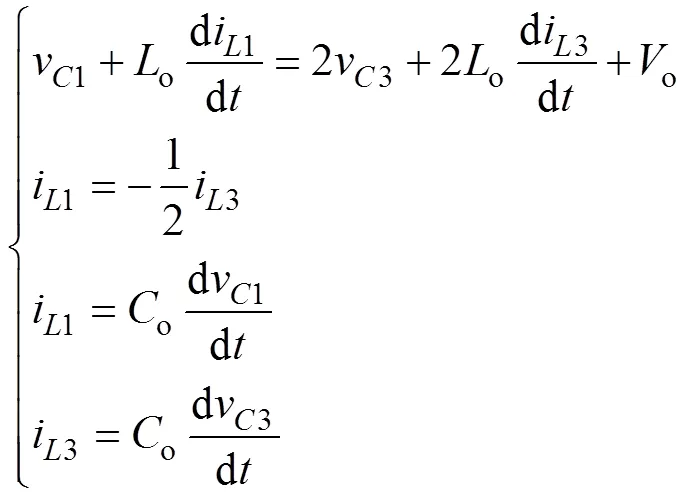
与此同时,0和1时刻电感电流和电容电压的初值表达式分别为


式中,v1min、v1max和v3max、v3min分别为1、3在0和1时刻对应电压值。
由式(1)~式(4)可得,模态1和模态2下电感电流和电容电压时域表达式分别为


式中,令=[1/(oo)]1/2;=v1max-2v3min-o。
在一个开关周期内,对于电容1存在
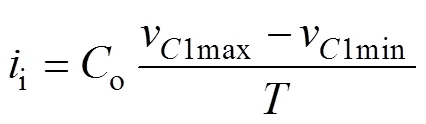
式中,i为输入电流平均值;为一个开关周期。综合式(5)~式(7)可得,0~1及1~2时的电感电流简化时域表达式分别为


经分析可知,前级电感1、2电流为后级电感3、4电流的1/2,并且方向相反。若采用4个独立电感,磁性元件占据空间较大,可以通过磁集成的方法来进行优化。前级电感和后级电感可以采用交错并联正向耦合,提升同级电感间耦合度,因此现将1、2和3、4分别交错绕制在磁心的两个边柱。前、后级间为减小彼此的干扰,可以通过解耦磁集成进行设计,由于前、后级电流方向相反,通过合理的绕制方向使中柱磁通进行部分抵消。4个电感设计时采用相同匝数和完全对称绕组以保证参数一致。
2 磁集成电感分析与设计
2.1 磁集成电感方法
谐振SCC包含4个电感元件,若采用独立电感,其主要缺点为损耗大、体积大。耦合磁集成电感结构如图4所示。图4a为独立电感结构,4个电感分别绕制在四个磁心上,该方法各电感均独立,互不干扰,但体积大、损耗大。由式(8)和式(9)可知,i1=i2、i3=i4,因此依据磁通抵消原理可将独立电感进行耦合磁集成,得到如图4b所示方案。该方案采用多磁柱磁心且结构对称,因此各电感数值相同。

图4 耦合磁集成电感结构
采用解耦磁集成方法可进一步减小磁心体积和损耗,解耦磁集成电感结构如图5所示。图中,1、2和0分别为磁心各磁柱流过磁通。变换器独立电感1、2和3、4由于其电流相同可形成两级耦合电感,如图5a所示。耦合电感使用的UU型磁心可以将两个靠近中心的边柱进行合并,进而得到磁集成后的单个EE型磁心,如图5b所示。但由于前后级电流大小不一致,中柱磁通不能完全抵消,因此不能将中间磁柱去掉,同时为了实现前后级间的解耦,中柱选择不开气隙。

图5 解耦磁集成电感结构
2.2 磁路—电路耦合数学模型分析
图6为耦合磁集成电感和解耦磁集成电感等效磁路。图中,1、2、3、4、0分别为各电感绕组在磁柱上产生的磁通,11、22、33、44分别为各绕组产生的磁动势,1、2、3、4、0分别为各磁柱等效磁阻。

图6 等效磁路
根据图6a可知,由于磁路对称,设1=2=3=4=,1=2=3=4=,则根据等效磁路和电磁感应定律可得各磁柱磁通1、2、3、4和加在4个绕组上的电压分别表示为

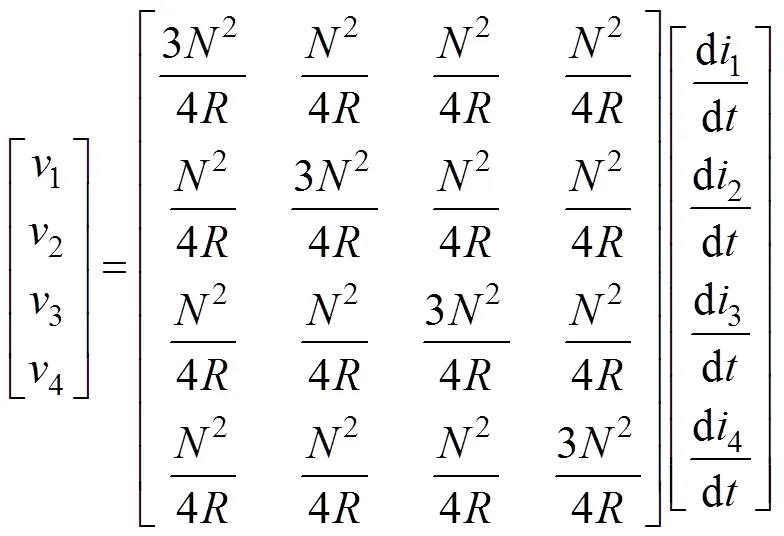
最后得到其各自感、互感及耦合系数分别为

式中,为各电感自感;为4个电感之间的互感;为电感间的耦合系数。
经理论分析,由于结构对称,4个电感数值大小相同,并取决于绕组匝数和磁阻大小。磁阻计算公式为=/(A),为气隙大小,为磁导率,为磁心有效截面积。因此,磁阻由气隙大小决定,可通过合理调整气隙来控制电感数值。
解耦磁集成根据图6b可得磁通1和2为

其中
=2+20
根据法拉第电磁感应定律=d/d可知,由于1=2、3=4,则加在绕组上的电压可以表示为

通过式(14),可表征采用解耦磁集成时,对应电感自感、互感以及耦合系数分别为

2.3 磁集成电感结构设计
耦合磁集成对于其磁通分布有两种方式,耦合磁集成结构如图7所示。图7a为交错耦合磁集成,与其磁通流向相同绕组反向耦合,其余绕组正向耦合,该方法不能实现直流磁通抵消;图7b为反向耦合磁集成,每相绕组均为反向耦合,可以实现直流磁通抵消。由式(12)可知,为实现相同电感数值,各电感匝数以及气隙大小需保持相同。耦合系数固定近似为1/3,反向耦合磁集成需要设计足够大数值电感才能实现最终效果,这会导致绕组损耗大大增加,因此本文采用交错耦合方法。

图7 耦合磁集成结构
采用解耦磁集成设计时,耦合电感可分为绕组非交叉排布和交叉排布两种结构,如图8所示,其中左侧磁柱旁深色为1,浅色为2,右侧磁柱旁深色为3,浅色为4。由于前后级电流不同,为防止磁通在中柱进行叠加后过大,选择两级耦合电感正向耦合方式。为获得更高耦合度,选择交叉排布方式。

图8 解耦磁集成排布方式
3 仿真分析及实验验证
3.1 仿真分析
本文基于谐振SCC设计磁集成电感,变换器参数见表1。采用Ansys Maxwell 3D有限元软件进行仿真证明,仿真结果见表2。由表2可知,耦合磁集成耦合系数约为0.33,解耦磁集成采用绕组交叉排布时耦合系数约为0.98,采用非交叉排布时耦合系数约为0.79,由此得出解耦磁集成采用交叉排布方式可以提高耦合度,同时能够实现两级解耦。
表1 变换器参数

Tab.1 Converter parameters
表2 仿真结果

Tab.2 Simulation results (单位: nH)
图9为独立电感、耦合磁集成和解耦磁集成三种方案气隙磁通密度仿真结果,图9a和图9b中,四段磁通密度数值分别为4个电感绕组所在磁柱气隙磁通密度,图9c为磁集成电感磁心两边柱气隙磁通密度和中柱磁通密度。由于后级电感电流为前级的2倍,所以后级磁通密度也约为前级的2倍。对于解耦磁集成方案,两边柱磁通在中柱进行叠加后部分抵消,叠加后中柱磁通密度与前级大小基本相同。三种方法气隙磁通密度最大值均小于峰值,仿真结果与理论分析相符,均满足设计要求。
图10为三种方案磁心磁通密度仿真结果,从图中可以得出,解耦磁集成方法磁心磁通密度分布更为均匀,磁心损耗更小,磁通密度主要集中在后级电感处,其最大值不超过400mT。

图9 气隙磁通密度仿真结果

图11为三种方法的损耗数值以及磁心体积对比。独立电感总损耗最大,耦合磁集成其次,但其磁柱较多导致磁心体积过大,仍不具优势。解耦磁集成总损耗最小,其磁心损耗大幅减小是降低总损耗的主要因素。与独立电感相比,解耦磁集成方法总损耗减小了约25%,体积下降了约50%。

图11 损耗和磁心体积对比
经综合对比分析,解耦磁集成总损耗最小,并且能大幅度缩小磁心体积,对于提升变换器的功率密度和效率更具优势,因此本文最终采用交叉绕组排布方式设计解耦磁集成电感。绕组的位置、宽度和绕制方向等都会对电感数值产生影响,为获得相同的电感磁性参数,设计电感时采用完全对称绕组排布方式,磁集成电感绕组结构如图12所示。

图12 磁集成电感绕组结构
3.2 实验验证
本文以谐振开关电容变换器为例,对所提磁集成电感设计实验样机并搭建相应实验平台,实验样机如图13所示。
用LRC电桥仪测得磁集成电感和独立电感测量结果见表3。从表中数据可以得出,传统独立电感很难保证各电感参数一致,采用完全对称绕组设计的磁集成电感能够有效解决参数不一致问题。

图13 实验样机
表3 电感测量结果

Tab.3 Inductor measurement results(单位: nH)
图14为所提磁集成电路设计工作于互补模式时所测得部分电流电压实验波形。由图可知,前后级电感电流谐振周期基本保持一致,实验所得各项参数与理论分析基本相符。图15为独立电感和磁集成电感谐振电感电流i3、i4和开关管电容电压S3、SDc波形。与独立电感相比,采用磁集成电感可以有效减小开关管的电压振荡,提升变换器稳态性能。
图16为独立电感和磁集成电感的效率曲线对比,其整体趋势均为先增大后减小,在50W获得效率最大值。磁集成电感效率始终高于独立电感,最高效率可达97.09%,与独立电感相比提升了1.671%。
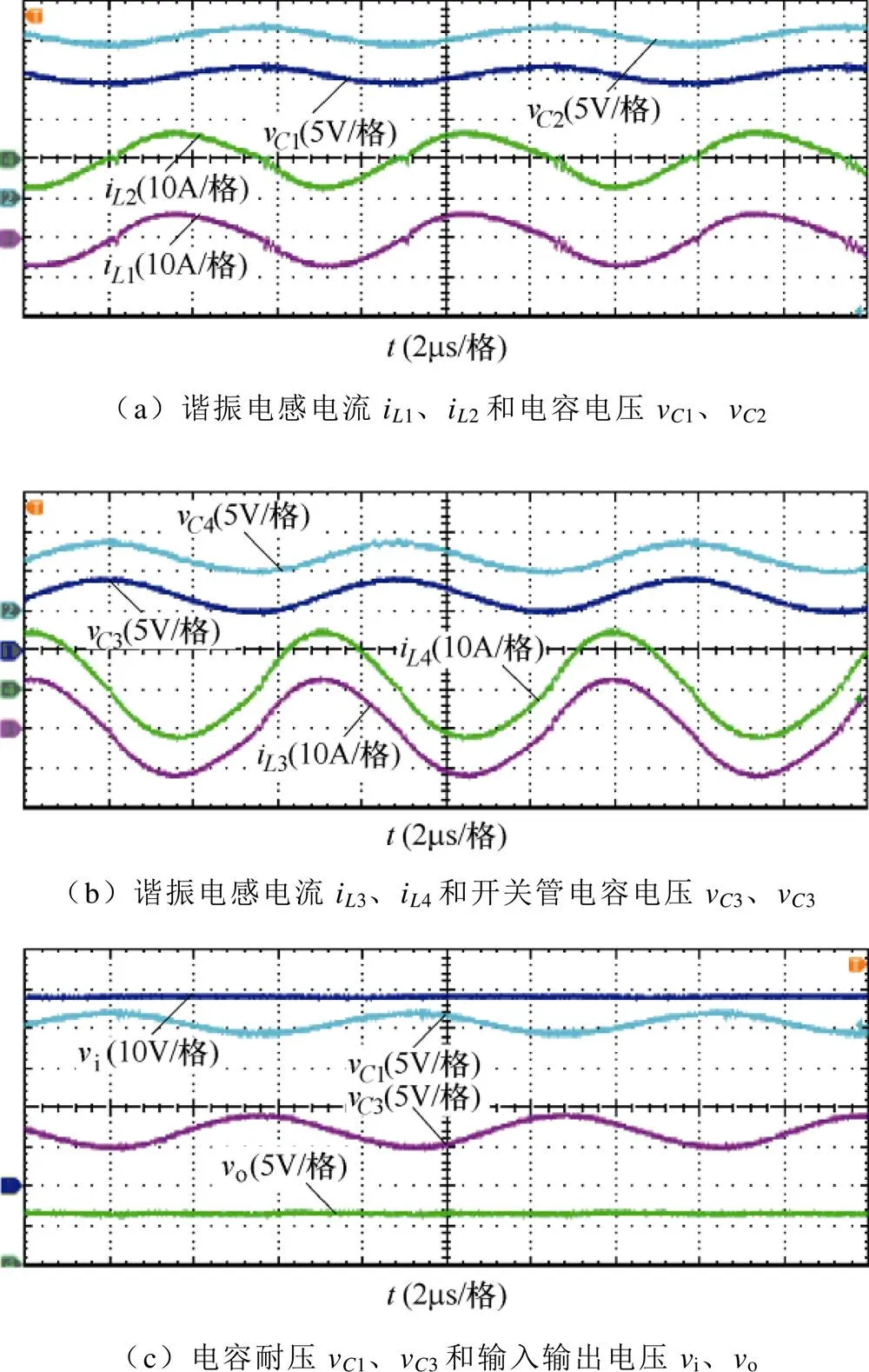
图14 变换器主要波形

图15 开关管电压波形对比
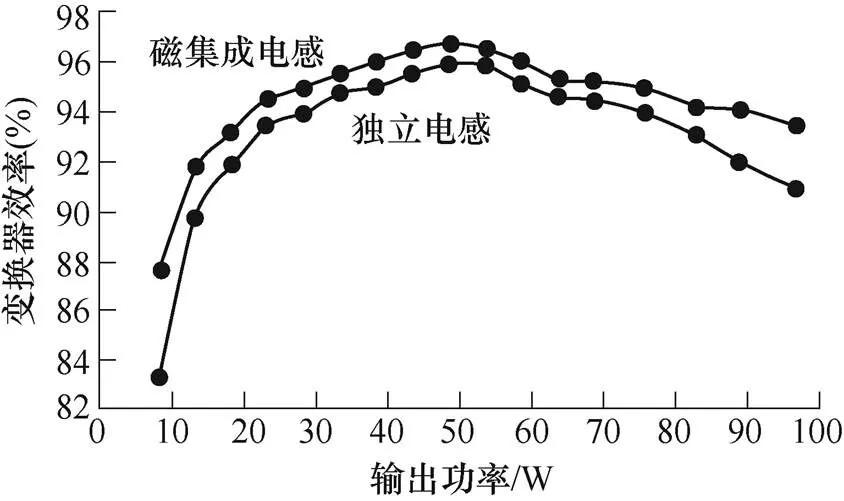
图16 效率曲线对比
4 结论
本文在分析了谐振SCC互补模式下前后级谐振电感间电流特性差异的基础上,建立数学模型并利用有限元仿真进行对比分析,设计了解耦磁集成电感。文中采用中柱不开气隙的方法能够抵消部分磁通,可以解决变换器前后级谐振电流不等导致的解耦困难问题。同时,采用完全对称绕组和交叉排布方式保证了电感参数的一致性,提高了电感间的耦合度。最后得出以下结论:
1)与耦合磁集成方案对比,谐振SCC电路中采用解耦磁集成方式占据体积更小、磁通密度分布更均匀,可有效降低损耗,对于提升变换器功率密度更具优势。
2)采用中柱不开气隙的两级耦合电感实现解耦磁集成,可以解决SCC电路前后两级电感电流不等导致的解耦困难问题。
3)为提高耦合度,电感间采用绕组交叉排布方式,利用完全对称绕组方法可减小绕组在设计时对磁性参数的影响,有效提升多个电感参数的一致性。
[1] Yeung Y P B, Cheng K W E, Ho S L, et al. Unified analysis of switched-capacitor resonant converters[J]. IEEE Transactions on Industrial Electronics, 2004, 51(4): 864-873.
[2] Stala R, Waradzyn Z, Mondzik A, et al. DC-DC high step-up converter with low count of switches based on resonant switched-capacitor topology[C]//2019 21st European Conference on Power Electronics and Applications (EPE'19 ECCE Europe), Genova, Italy, 2019: 1-10.
[3] Cao Dong, Peng Fangzheng. Zero-current-switching multilevel modular switched-capacitor DC-DC con- verter[C]//2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, 2009: 3516-3522.
[4] 温飘, 杨晓峰, 闫成章, 等. 一种基于SiC器件的谐振开关电容变换器[J]. 中国电机工程学报, 2020, 40(24): 8111-8122.
Wen Piao, Yang Xiaofeng, Yan Chengzhang, et al. A SiC modules based resonant switched capacitor converter [J]. Proceedings of the CSEE, 2020, 40(24): 8111-8122.
[5] Li Shouxiang, Kang Xianglin, Zheng Yifei, et al. Analysis and design of the ladder resonant switched- capacitor converters for regulated output voltage applications[J]. IEEE Transactions on Industrial Elec- tronics, 2017, 64(10): 7769-7779.
[6] 吴学智, 祁静静, 刘京斗, 等. 谐振开关电容DC/DC变换器拓扑研究综述[J]. 中国电机工程学报, 2021, 41(2): 655-666.
Wu Xuezhi, Qi Jingjing, Liu Jingdou, et al. Review of topological research on resonant switched capacitor DC/DC converter[J]. Proceedings of the CSEE, 2021, 41(2): 655-666.
[7] 李洪珠, 曹人众, 张垒, 等. 磁集成开关电感交错并联Buck/Boost变换器[J]. 电机与控制学报, 2018, 22(6): 87-95.
Li Hongzhu, Cao Renzhong, Zhang Lei, et al. Integrated magnetic and switch inductance staggered parallel of Buck/Boost converter[J]. Electric Machines and Control, 2018, 22(6): 87-95.
[8] 王议锋, 刘瑞欣, 韩富强, 等. CLTLC多谐振变换器的磁集成方法[J]. 电工技术学报, 2022, 37(2): 380-388.
Wang Yifeng, Liu Ruixin, Han Fuqiang, et al. Magnetic integration method for CLTLC multi- resonant converter[J]. Transactions of China Electro- technical Society, 2022, 37(2): 380-388.
[9] 肖龙, 伍梁, 李新, 等. 高频LLC变换器平面磁集成矩阵变压器的优化设计[J]. 电工技术学报, 2020, 35(4): 758-766.
Xiao Long, Wu Liang, Li Xin, et al. Optimal design of planar magnetic integrated matrix transformer for high frequency LLC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 758-766.
[10] Sagpazar N B, Cho W, Kim K, et al. Three-level resonant switched capacitor Boost converter[C]// International Conference on Power Electronics and ECCE Asia, Seoul, Korea, 2019: 2868-2873.
[11] 闫成章, 杨晓峰, 刘妍, 等. 基于移相控制的谐振开关电容变换器占空比优化策略[J]. 电工技术学报, 2021, 36(增刊2): 676-687.
Yan Chengzhang, Yang Xiaofeng, Liu Yan, et al. Duty cycle optimization of phase shift control based on resonant switched capacitor converter[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(S2): 676-687.
[12] Liu Y, Jiang S, Liang W, et al. Modeling and design of the magnetic integration of single- and multi-stage EMI filters[J]. IEEE Transactions on Power Electro- nics, 2019, 35(1): 276-288.
[13] 苏冰, 王玉斌, 王璠, 等. 基于耦合电感的多相交错并联双向DC-DC变换器及其均流控制[J]. 电工技术学报, 2020, 35(20): 4336-4349.
Su Bin, Wang Yubin, Wang Fan, et al. Multi-phase interleaved bidirectional DC-DC converter with coupled inductors and current sharing control strategy[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4336-4349.
[14] 李洪珠, 刘飞扬, 刘艳, 等. 一种新型磁集成高增益耦合电感倍压Boost变换器[J]. 电工技术学报, 2020, 35(增刊2): 450-460.
Li Hongzhu, Liu Feiyang, Liu Yan, et al. A new magnetically integrated high gain coupled inductance voltage-doubled Boost converter[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 450- 460.
[15] Zumel P, Garcia O, et al. Magnetic integration for interleaved converters[C]//IEEE Applied Power Elec- tronics Conference & Exposition, Miami Beach, FL, 2003: 1143-1149.
[16] 杨玉岗, 张书淇, 苗闯, 等. 交错并联磁耦合双向直流变换器中多相耦合电感的设计准则[J]. 电源学报, 2018, 16(3): 28-35, 53.
Yang Yugang, Zhang Shuqi, Miao Chuang, et al. Design criterion for multi-phase coupled inductors in magnetically integrated interleaving bidirectional DC-DC converter[J]. Journal of Power Supply, 2018, 16(3): 28-35, 53.
[17] 高圣伟, 王浩, 刘晓明, 等. 新型磁集成双频DC/DC变换器[J]. 中国电机工程学报, 2020, 40(24): 8131- 8144.
Gao Shengwei, Wang Hao, Liu Xiaoming, et al. A novel double frequency DC/DC converter with magnetic integration[J]. Proceedings of the CSEE, 2020, 40(24): 8131-8144.
Design of Magnetic Integrated Inductor for Resonant Switched Capacitor Converter
112111
(1. National Active Distribution Network Technology Research Center Beijing Jiaotong University Beijing 100044 China 2. Shenzhen Power Supply Co. Ltd Shenzhen 518001 China)
Since resonant switched capacitor converter can realize zero-current switching, reduce switching loss, and improve power density, it is widely used in high power density and gain ratio applications such as data centers and electric vehicles. As an essential part of SCC, the inductor is a crucial factor affecting the improvement of converter performance. To solve the decoupling problem of unequal resonance currents of the front and second stages of the converter, this paper designs the decoupled magnetic integrated inductor without opening the air gap in the center column. Based on the analysis of the working principle of the circuit, compared with the coupled magnetic integration, the decoupled magnetic integration method without an air gap in the center column has a higher inductance coupling degree and can achieve two-stage decoupling. The asymmetry of the resonant parameters of the converter will lead to inconsistent resonant periods of the front and second stages. In this paper, the complete symmetrical winding is used to reduce the influence of the windings on the magnetic parameters, which can effectively ensure the consistency of multiple inductor parameters. Finally, the experimental prototype is built to verify the rationality and effectiveness of the designed resonant SCC magnetic integrated inductor.
Coupled inductor, decoupled magnetic integration, complete symmetrical winding, resonant switched capacitor converter
10.19595/j.cnki.1000-6753.tces.220387
TM46
面向大规模可再生能源消纳的城市建筑与电网互动关键技术研究与应用资助项目(090000KK52210134)。
2022-03-17
2022-05-20
李紫薇 女,1998年生,硕士,研究方向为磁集成技术。E-mail: 20121472@bjtu.edu.cn
续文政 男,1992年生,讲师,硕士生导师,研究方向为电力电子变换器、无线电能传输和交通电气化等。E-mail: xuwenzheng@bjtu.edu.cn(通信作者)
(编辑 陈 诚)
