基于动态WSN中分簇脉冲耦合时间同步开销研究

莫文婷

（安徽文达信息工程学院，安徽 合肥 230000）

WSN的研究起步于20世纪90年代末，当无线自组网络技术日趋成熟时，无线通信、微电子、传感技术也得到快速发展，如何将无线自组网与传感技术相结合的课题成为热点，即无线传感器网络的研究。无线传感网络中节点之间相互交流与信息交换需要时间同步，因此时间同步是一项重要的技术支持。

目前，时间同步方法主要分3类：基于发送者的同步，如FTSP；基于发送者-接收者的同步，如TPSN，基于接收者-接收者的时间同步，如RBS。这些经典时间同步算法在时间上都能达到有效的同步。在工业、农业等无线传感器利用中，为了节约成本以及能更大范围采集网络中的数据，传感器点节点不断移动，网络点拓扑结构不断，在动态WSN网络中以上的同步算法不能很好解决时间同步问题。因此对于动态WSN，文章提出动态脉冲耦合 振 荡 器（Moving Pulse Coupled Oscillator，MPCOs），因网络范围比较大，大范围传感器节点同步开销比较大，可以先局部同步，再整体传感器节点同步，因此在MPCOs基础上进行优化，提出分簇型 MPCOs（Clustering -Moving Pulse Coupled Oscillator）算法，解决网络负担、通信开销，提高时间同步速度，使同步具有针对性和方向性。

1 MPCOs模型

移动式脉冲耦合振荡器是在脉冲耦合振荡器基础上根据网络情况进行优化，在动态的无线传感器网络中，通过传感器点节点不断移动采集网络中数据，网络中点拓扑结构不断发生变化，而MPCOs模型具有自组织、无记忆网络同步模型，则很好应用于动态无线传感器网络则。文章中，采用在网络中W= (I,E)有N个节点（节点设置I= { 1 ,2,3…N}并且E⊂I×I），所有节点在二维空间（L×L）以周期性相同、速度为V的相同速度进行移动，同时它们的初始相位角是随机确定。令相位φi是节点i的相位变量，因为周期T与相位关系为那么节点i的位置变化为和状态变量的分别是下式（1）和（2）：

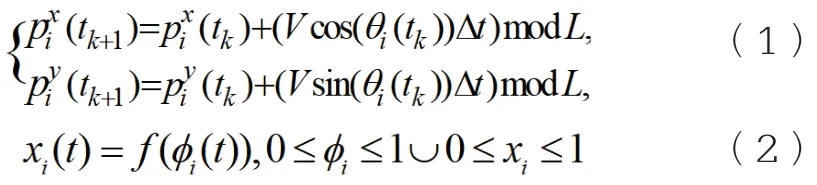
当节点i的状态和相位在时间t内达到1，它将激发一个信号强度为ε的脉冲。那么节点j状态增加ε达到状态xj，方向相位角θj随机变化，节点随机分布。因此，得（3）式：

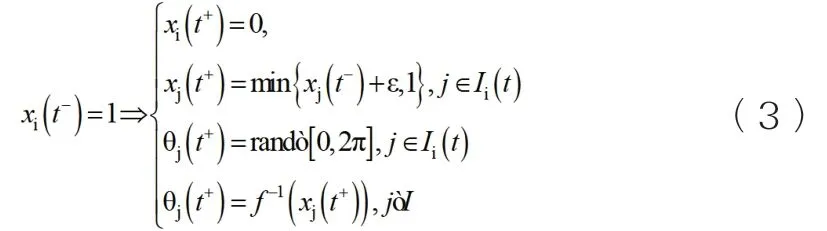
从式（3）可以看出，在任意均匀分布间隔为[0，2π]内，状态变化是任意的。x（t+）表示接收脉冲信号后的状态，x（t-）是接收脉冲信号前的状态。通过更新所有传感器节点的相位，使所有节点时间达到同步。

2 分簇型MPCOs步骤

为减轻网络负担与开销，在MPCOs模型基础上提出分簇型算法。实现WSN整个网络的同步，需要包括主要的内容包括：簇内节点的时间同步；簇间节点的时间同步，最终实现整个网络时间同步。

步骤1：确定最优簇头数目mbest，计算方法如下公式：

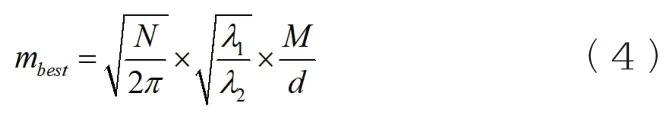
其中，mbest为簇头数目；N为无线传感网络的节点数目；λ1为MPCOs模型固定属性值为4.965 1；λ2为另一个MPCOs模型固定属性值为4.865 1；M为网络监测区域范围；d为监测区域与汇聚节点的距离。

步骤2：利用基于距离的K-MEANS聚类算法生成mbest个簇头节点，以通信开销最小为形成簇的准则。

步骤3：形成簇头节点后，利用邻居握手协议（NHP）形成簇。

步骤4：根据MPCOs模型先实现簇内同步，然后再实现簇间之间时间同步。

3 C-MPCOs算法

4 仿真结果分析

MPCOs模型利用状态函数：

仿真分析速度V、耦合强度ε以及耦合节点通信半径R对时间同步时间的影响。讨论传感器节点为N=4个，速度为V=[22 26 30 34 38 40]m/s，半径R=[20 22 24 26 28 30 32 34 36 38 40]m，可以采取不同的耦合强度，文章中耦合强度ε=0.04的情况。根据算法得到如下仿真图1R-T。

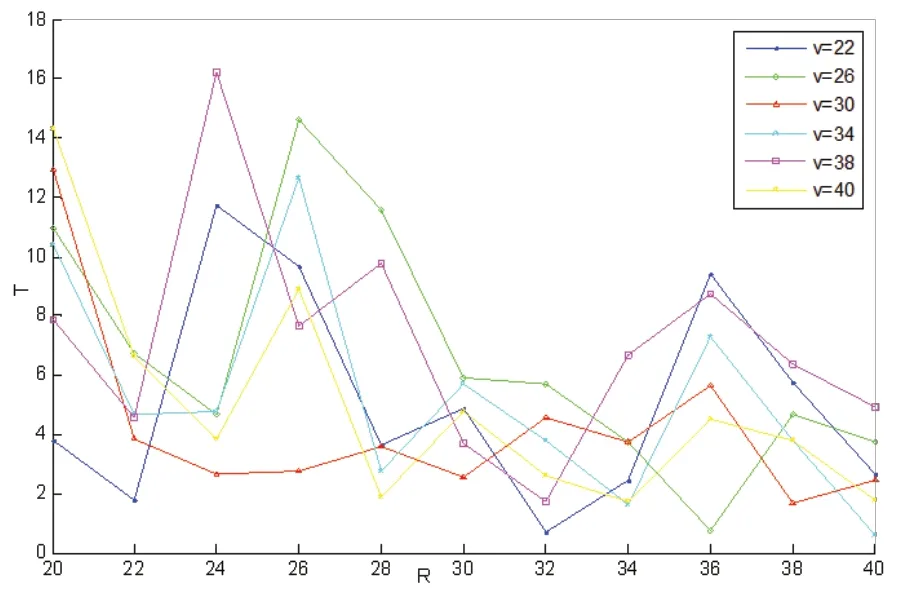
图1 R-T

N=4，ε=0.04

仿真结果图1分别是在节点N=4，耦合强度ε=0.04仿真图。讨论速度为V=[22 26 30 34 38 40]m/s，半径R=[20 22 24 26 28 30 32 34 36 38 40]m时，同步时间与它们之间关系。从仿真图可以看出总体趋势，在某段通信半径范围内，随着半径范围的增加，刚开始同步时间在十几秒以上，随着半径范围点增加，在半径为40 m时，同步时间缩小为6 s以下，同步时间明显比比较范围小的同步时间快，即同步半径越大同步时间越快；对于速度相对而言，速度为40 m/s与22 m/s的整体同步时间要快，即速度越大的整体点同步时间越快，则速度越大同步时间速率收敛越快。因此速度和通信半径与同步时间收敛速度成正比。

最终将MPCOs模型应用到WSN中，同时将网络分为多个簇，在一个簇内达到同步后，再将各个簇再进行整体同步。根据上述仿真在100 m×100 m区域内，选最佳参数节点数N=8、耦合强度ε=0.04、通信半径R=40 m、速度V=34 m/s，进行仿真后得同步时间为Tsync=2.337 9 s。对N=8个节点进行分簇，根据公式（4）计算得到簇头节点为2，则分为两个簇x1、x2，进行仿真后如图2（a）、图2（b），图2（a）中不同点颜色表示振荡器不同步，最后所有节点颜色相同，则所有传感器节点都达到同步状态，如图2（b）。

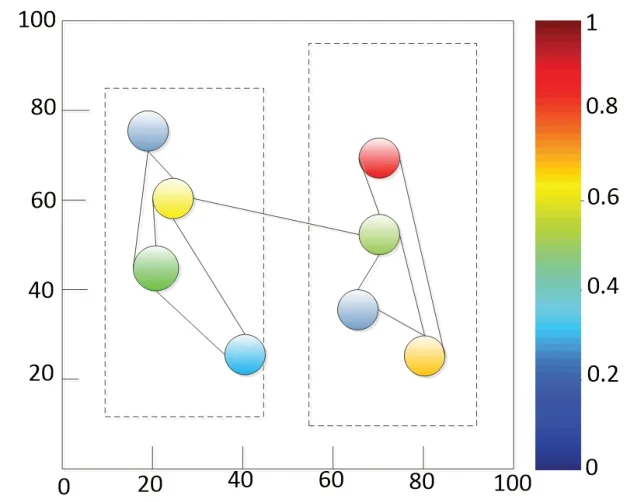
图2（a） 振荡器节点不同时状态图

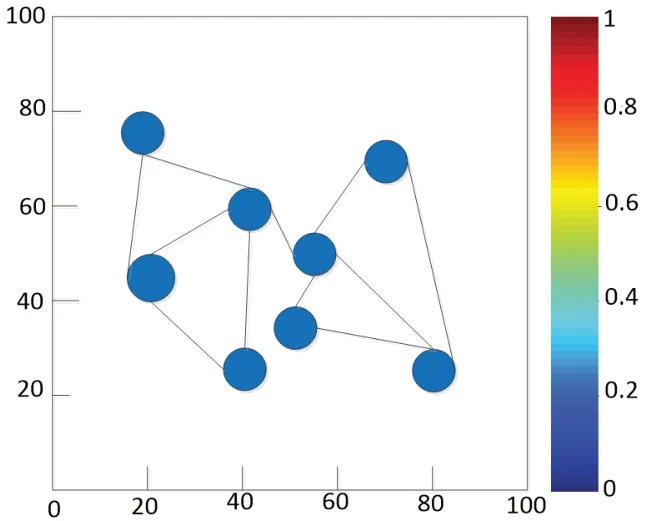
图2（b） 振荡器节点同步状态图

根据MPCOs模型仿真得到最优参数，再将最优参数应用C-MPCOs算法进行仿真，如图3所示，簇x1、簇x2同步后的同步时间为Tsync=0.667，相比于MPCOs模型时间同步快了1.670 9 s，有效点缩短了同步时间，减小网络开销。

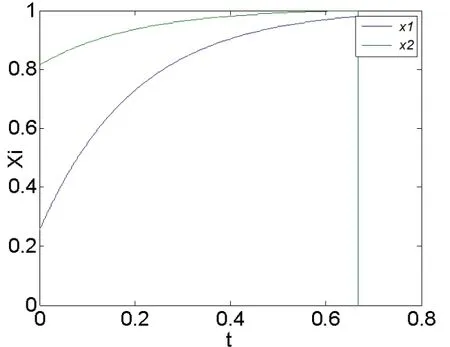
图3 Xi—t

5 总结

文章在MPCOs模型基础上进行优化提出C-MPCOs算法提高同步时间，从而有效减少网络开销。通过MPCOs模型仿真在确定参数最优情况下，再根据C-MPCOs算法进行仿真。通过仿真验证了C-MPCOs算法明显相比于MPCOs算法同步时间提高，有效减小网络负担和同步开销，使同步更具有方向性。文章模型能很好在二维动态相互交互平面进行时间同步，对于三维空间需更进一步研究。