孔板压降的内角影响机理分析及计算公式改进
2023-01-09李浩冉张则亮白长青
李浩冉,刘 磊,张则亮,白长青
(1.西安交通大学 机械结构强度与振动国家重点实验室/陕西省先进飞行器服役环境与控制重点实验室,西安 710049;2.中国石油天然气股份有限公司大连石化分公司,大连 116031)
0 引言
孔板作为重要的计量或节流部件,在工业管道系统中具有广泛应用。当流体流经孔板时,流束在孔板处形成局部收缩,从而使流速增加,压力降低,于是在孔板前、后产生了压力降,介质流动的流量越大,在孔板前、后产生的压降就越大。经过大量的试验,国内、外研究人员总结了孔板流量与压降关系的诸多计算公式,并体现在规范中。
目前对于孔板压降的研究,主要集中考虑孔板孔径比与孔板厚度对压降的影响。GERD[1]理论推导了标准孔板压力损失与直径比的关系;GAN等[2]利用CFD模拟分析了孔板厚度对压力损失系数的影响;其他学者[3-5]也同样得出了孔板压力损失随孔板厚度的增加而减小的结论;喻兰兰等[6]研究发现节流孔板的入口倒角、出口倒角、孔径和厚度等结构参数对孔板壁面附近的最大压降幅度和孔板节流效果的影响不同;MAYNES等[7]试验研究了水流过不同结构多孔扳时的压损特性,主要分析了等效直径比与相对厚度对多孔扳压力损失的影响;AI等[8]通过数值计算和模型试验,提出了考虑厚度影响的无内角孔板能量损失系数的计算式。但这些研究中均没有考虑内角对孔板压降或流量的影响。
近年来,有学者已经注意到孔板内角对孔板压降的影响。周云龙等[9]研究了锥形孔板的锥角对孔板流出系数的影响;DUZ[10]通过数值计算研究了负内角孔板对孔板能量损失的影响;涂俊[11]和华兰[12]各自研究了孔板内角对空气和燃气孔板压降的影响;吕福炜等[13]则研究了同为节流元件的文丘里管渐扩段、渐缩段角度为稳流特性的影响;门晓苏等[14]通过实验研究了孔板内角对空气孔板压降的影响,得出负内角孔板造成的压力降显著低于无内角孔板和正内角孔板的结论。上述孔板内角对其压降的影响研究表明孔板内角对孔板压降有着显著影响,但是并没有给出适用于工程设计使用的考虑内角影响的孔板压降或流量计算公式。
本文首先建立了研究孔板压降内角影响的CFD仿真模型,通过比较CFD结果与已有文献中实验数据,验证了CFD仿真模型的合理性和可靠性。分析了孔板压降的内角影响机理及规律,得出考虑孔板内角影响的孔板压降改进计算公式。
1 CFD仿真建模及模型验证
根据现有文献中孔板-管路试验系统建立相应的CFD仿真模型,并进行网格无关性验证。通过与文献试验数据比较,验证了CFD仿真模型的合理可靠性。
1.1 仿真建模
如图1所示,孔板-管路系统由孔板、管路及容器组成,其中l1,l2,l3和l4为各段管路及容器的长度,h为容器高度,D为管路的内径。d,b,α分别为孔板内径、孔板厚度和孔板内角。沿气流方向,使孔板流通面积增大的α定义为正内角,反之为负。定义孔板直径与管路直径之比β=d/D,孔板厚度与管路直径之比γ=b/D。管路内空气的三维流动具有轴对称特性,因此可根据对称性选取系统流场的上半部分建立二维CFD仿真模型。采用FLUENT软件,对二维模型进行网格划分。图2示出网格划分后孔板附近区域的有限体积模型。

图1 孔板-管路系统示意Fig.1 Schematic diagram of orifice-pipeline system
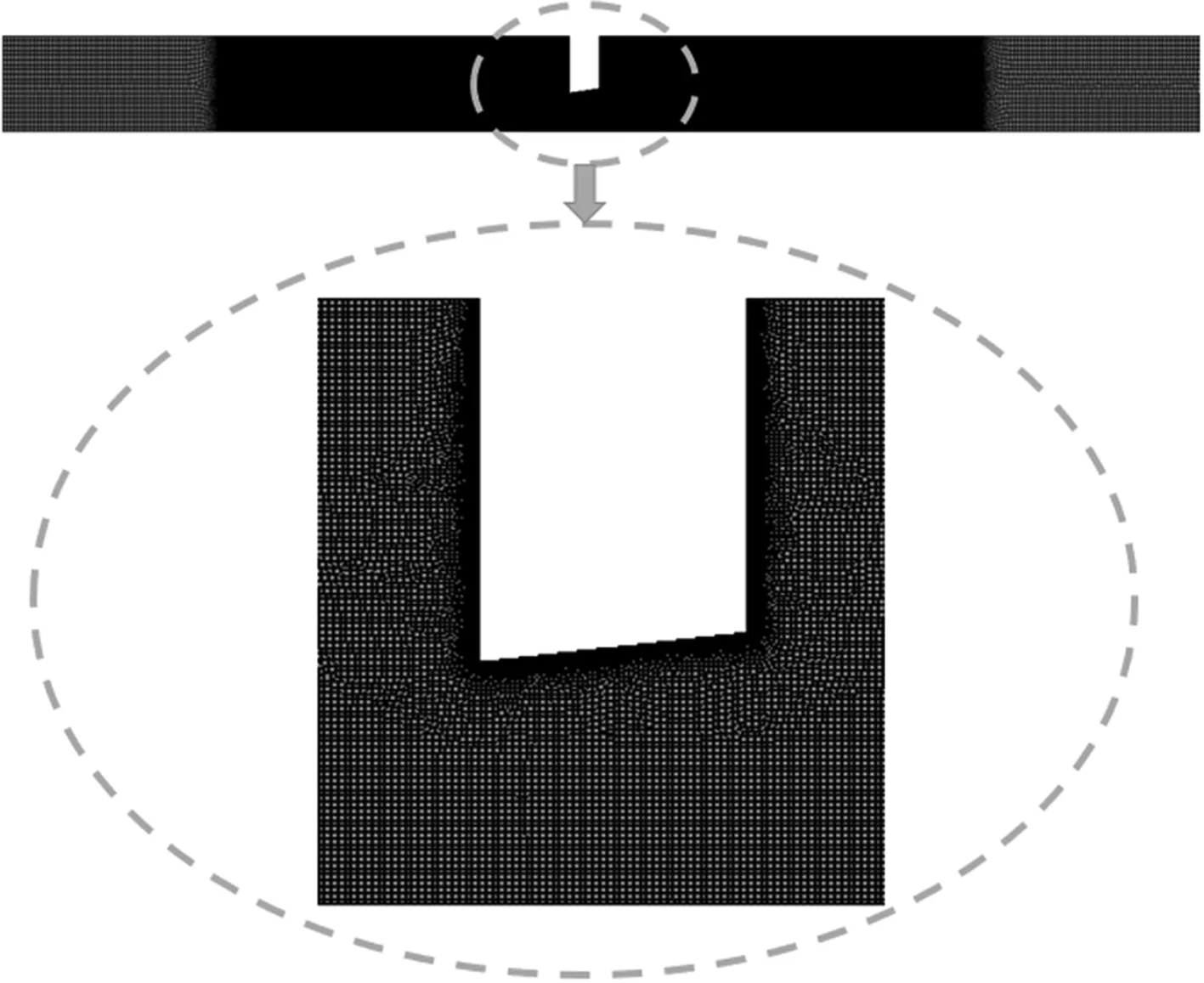
图2 二维有限体积模型局部Fig.2 Local diagram of the two-dimensional finite volume model
流动模型选择Standard湍流模型,压力和速度的耦合采用SIMPLE算法。入口采用质量流量边界条件,出口为压力边界条件。按照文献[14]中的试验装置参数以及压气机速度表达式,入口质量流量W的表达式为:

1.2 网格划分及网格无关性检验
网格全局参数大小设置为1 mm,对孔板前后各2.5D的范围进行局部加密,设置3种网格大小M1=0.5 mm,M2=0.2 mm 和 M3=0.1 mm;并对贴近孔板壁面流场进行再次局部加密,设置3种网格大小N1=0.1 mm、N2=0.05 mm和N3=0.01 mm。
按照径距取压的要求,分别在孔板前D处和孔板后D/2处设置2个监测点,如图1所示。选择监测点1和2之间的压降作为网格无关性检验的度量。网格无关性验证结果见表1。局部网格参数组合按网格数量升序排列,(M1,N1)网格数量最小,(M3,N3)网格数量最大,误差为与上一局部网格参数组合之间的压降误差。
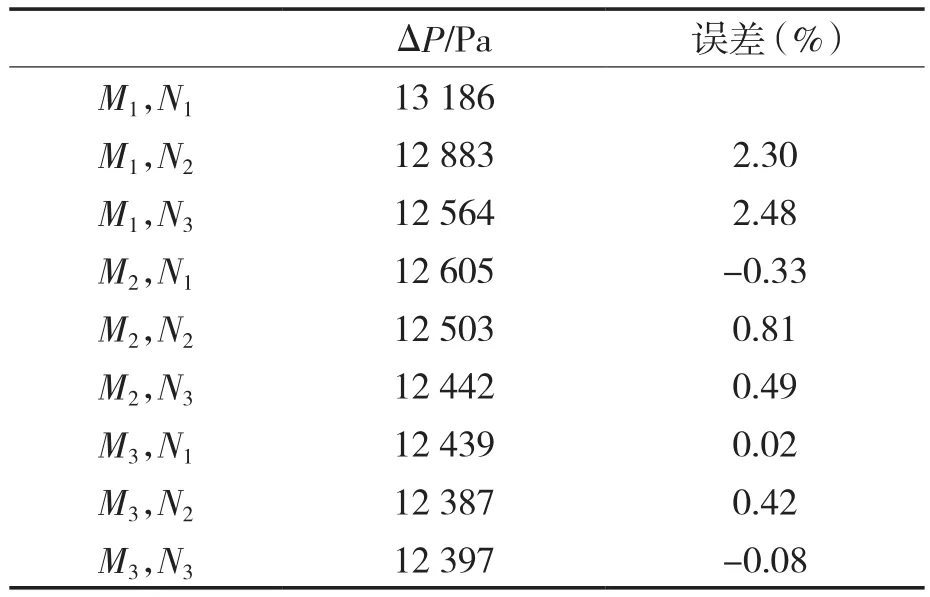
表1 网格无关性验证Tab.1 Grid independence verification
可以看出,局部网格参数组合(M3,N1)和(M2,N3)之间的误差为 0.02%,显著小于(M2,N3)和(M2,N2)之间的误差 0.49%。相比(M2,N3),采用网格数更多的(M3,N1),对提高计算精度的作用很小,反而增加了计算时间。因此,综合计算精度和计算时间,选择M2=0.2 mm,N3=0.01 mm的局部网格参数进行网格划分,以D=40 mm,β=0.5,α =10°,γ =0.2的模型为例,其网格数量为208 050。
1.3 CFD仿真模型验证
根据所建立CFD模型进行数值仿真,图3示出为不同孔径比和孔板内角下孔板压降数值计算结果与文献[14]中试验数据的对比。

图3 孔板压降仿真结果与文献[14]试验数据对比Fig.3 Comparison between simulation results of orifice plate pressure drop and experiment data in reference[14]
从图3可以看出,本文所建立CFD仿真模型计算结果与已有试验数据基本吻合。仅有图3(b)中孔板内角为5°和10°的2个数据点相差较大,通过不同结构参数的孔板压降数值计算结果对比以及流动机理分析,可以认为这2个试验数据误差较大主要是因为试验误差造成。除此之外,其它仿真计算结果与试验数据最大误差不超过2.82%,表明所建立CFD仿真模型是合理的,可以有效进行孔板压降预测。
由图3(b)可以看出,仿真结果和试验数据均表明内角对孔板压降有显著影响。CFD仿真结果中,正内角影响孔板压降最大值为4 314.7 Pa,达到无内角孔板压降值的33.88%;负内角影响孔板压降最大值为2 351.3 Pa,达到无内角孔板压降值的18.46%。
由图3(b)还可以看出,孔板内角为正内角时,随着内角角度值的增大,压降逐渐增大,且角度值越大,增大越缓慢,当内角接近45°时,压降值已趋于稳定;孔板内角为负内角时,随内角绝对值的增大,压降先减小后增大,在-10°左右取得最小值。总之,在-45°~45°的内角范围内,随着孔板内角值的增大,压降先减小后增大,最后趋于不变。
2 孔板压降的内角影响机理及规律
考虑空气的可压缩性,其伯努利方程为:

连续性方程以及等熵过程方程分别为:

式中 ρ ——密度,kg/m3;
1,2——下标,监测点1和监测点2;
A ——流束截面积,m2;
v ——速度,m/s;
P ——压力,Pa;
κ ——气体的等熵指数。
联立式(2)(3),可得
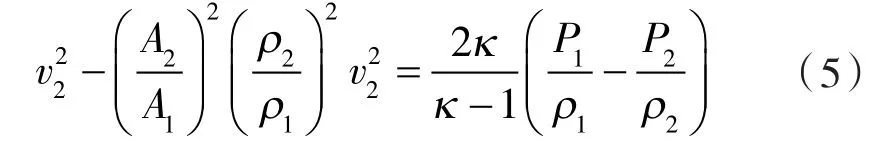
再将式(4)代入式(5),得监测点2速度计算公式为:

设μ=A2/A0为流束收缩系数,其中A0为孔板开孔最窄处面积,m2。由式(6)可得质量流量表达式为:

根据实际气体状态方程pv=ZnRT(Z为压缩系数)可知:

式中 M ——气体分子量;
Z ——压缩系数;
R ——理想气体常数;
T ——气体温度,K。
将式(8)代入式(7)得:
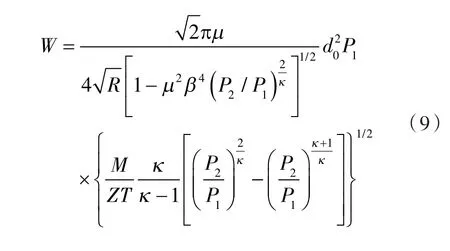
式(9)经过适当整理和简化后,可以得到目前国内常用的标准孔板的气体流量计算公式为:
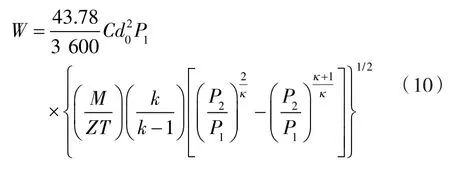
式中 C ——孔板流量系数;
d0——孔板直径,m。

图4 孔板处流体的速度云图Fig.4 Velocity nephogram of fluid at orifice plate

图5 正、负内角孔板处的流束截面积示意Fig.5 Schematic diagram of cross sectional area of flow beam at orifice plate with positive and negative inner angles
监测点2处沿半径方向r上的轴向速度分布如图6所示。图6示出虚线连接了各条曲线开始下降的临界点,反映了各角度下主流束截面积的变化。

图6 监测点2处轴向速度沿r方向的变化Fig.6 Variation of axial velocity in r-direction at monitoring point 2
由图6可以得出孔板内角对压降的影响机理:正内角和无内角孔板附近流体为突缩的流动状态,随着内角绝对值的增大,监测点2处的主流束截面积减小,速度增大,进而导致压降变大,如图 3(b)示出0°~45°的压降结果;小负内角孔板附近流体为由突缩到渐缩的过渡状态,随着内角绝对值的增大,监测点2处的主流束截面积增大,速度减小,进而导致压降变小,如图3(b)中0°~-10°的压降结果;大负内角孔板时的流体为渐缩的流动状态,随着内角绝对值的增大,监测点2处的主流束截面积减小,速度增大,进而导致压降变大,如图 3(b)示出-15°~-45°的压降结果。
标准孔板的内角规定为45°,故现有孔板流量规范式(10)适用于内角为45°的孔板。引入压降比 ΔP/ΔP45°,即各角度的压降与α =45°的压降之比,来研究β和γ对孔板压降与内角关系的影响。图7,8分别示出了β和γ对压降与孔板内角关系的影响。
由图7可以看出,不同β下,压降比随内角的变化趋势基本一致,但压降比数值略有差异,且这种差异会随孔板内角绝对值的减小而增大。当α=0°时,不同β下的压降比差异最大,压降比随着β的增大而增大;当α=±45°时,不同β下的压降比基本相同,无明显差异。

图7 不同β下孔板内角对压降比的影响Fig.7 Influence of inner angle α of orifice plate on pressure drop under different β
由图8可以看出,不同γ下,压降比随内角的变化趋势同样一致,但压降比数值差异较大,且这种差异同样会随孔板内角绝对值的减小而增大。当α=0°时,不同γ下的压降比差异最大,压降比随着γ的减小而增大;当α=-45°时,不同γ下的压降比差异相较α=0°时缩小,压降比仍随着γ的减小而增大。
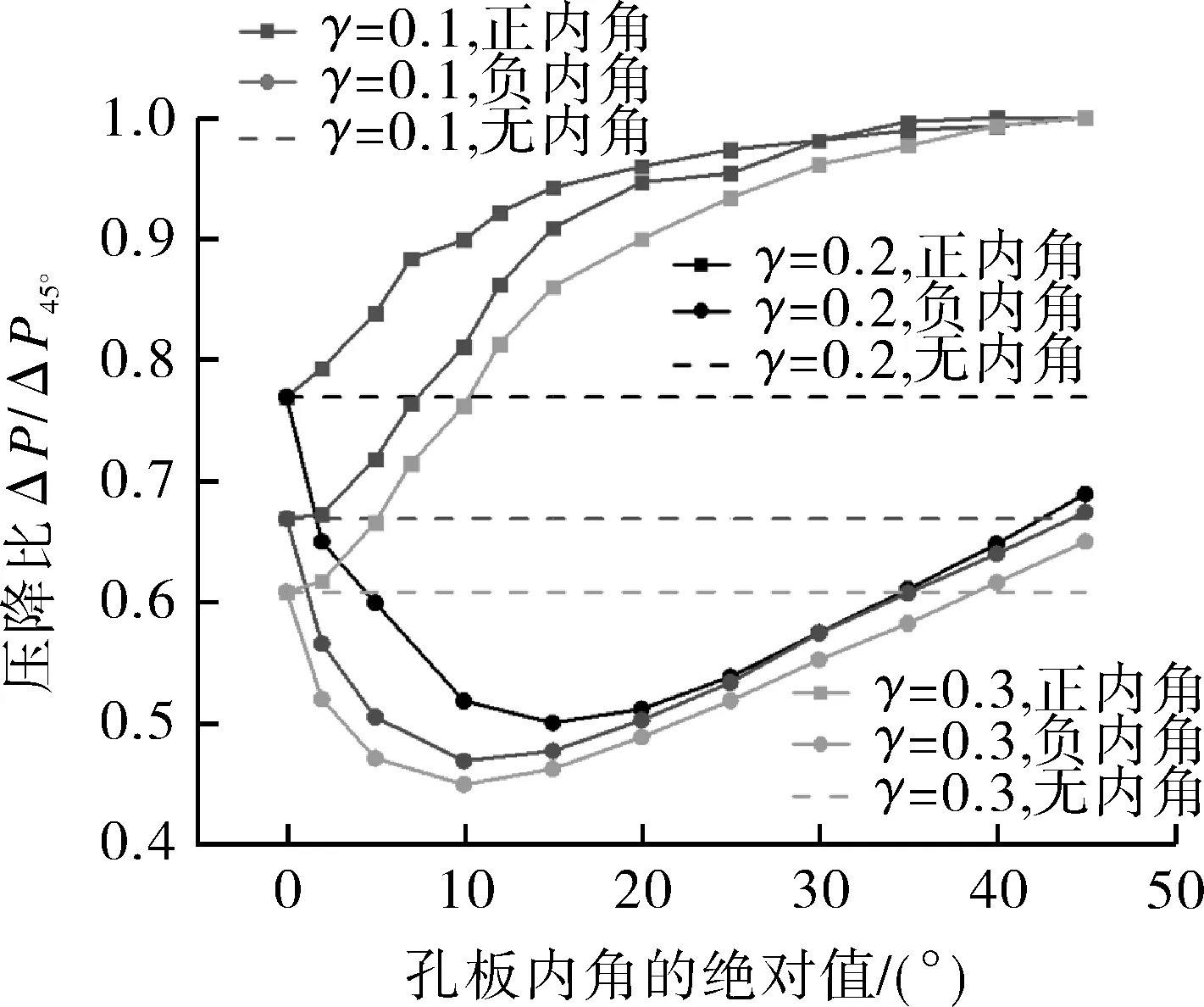
图 8 不同γ下孔板内角对压降比的影响Fig.8 Influence of inner angle α of orifice plate on pressure drop under different γ
3 考虑内角影响的孔板压降改进公式
在上述孔板内角对其压降影响机理及规律分析的基础上,结合规范式(10),提出孔板压降与流量关系的改进公式如下:

式(13)是根据内角影响机理,在各结构参数下大量数值计算结果统计基础上获得的内角修正系数计算表达式。
在同样的孔径比和孔板厚度下,本文提出公式与数值仿真和文献试验的误差见表2。

表2 本文公式与仿真和文献结果误差对比Tab.2 The error comparison between the proposed formula and numerical simulation and experimental data in the literature
从表中可以看出,绝大部分数据点误差在-5%~5%之间,反映出整体数据的误差较小。由此可以看出,本文提出的计算公式与数值计算和文献试验结果吻合良好,验证了本文提出的计算公式的准确性和可靠性。
4 结论
(1)孔板内角对压降有着显著影响,在-45°~45°的内角范围内,随着孔板内角值的增大,压降先减小后增大,最后趋于不变,存在压降最小值。
(2)孔板内角影响其压降的机理为:通过改变孔板处流体的流动状态,来影响孔板后的主流束截面积,进而改变孔板后流体速度,使孔板前、后压降产生变化。
(3)在已有规范公式的基础上,提出针对空气介质的考虑孔板内角影响的孔板压降与流量关系公式,并验证了该公式的准确性。
(4)本文提出公式和数值仿真结果均表明:不同孔径比和孔板厚度下,孔板内角对压降的影响关系有所差异,且这种差异随着孔板内角绝对值的减小而增大。
