ON (a ,3)-METRICS OF CONSTANT FLAG CURVATURE*
2023-01-09GuangzuCHEN陈光祖
Guangzu CHEN (陈光祖)
School of Science,East China JiaoTong Uniuersity,Nanchang 330013,China E-mail : chenguangzu1@163.com Xinyue CHENG(程新跃)*
School of Mathematical Sciences,Chongqing Normal Universitg,Chongqing 401331,China E-mail: chengxy@cqnu.edu.cn


The study of Finsler metrics of constant flag curvature has a long history. In 1977, H.Yasuda and H. Shimada studied the classification problem on Randers metrics of constant flag curvature([12]). Later,D.Bao,C.Robles and Z.Shen completely classified Randers metrics of constant flag curvature by using the navigation technique([3]). Furthermore,R.Yoshikawa and S. V. Sabau obtained the classification theorem on Kropina metrics of constant flag curvature([8]). In addition to this, L. Zhou proved that the square metrics of constant flag curvature must be projectively flat ([13]). In [11], Shen-Yildirim classified the projectively flat square metrics of constant flag curvature. Thus the local constructions of square metrics of constant flag curvature have been determined completely. However,the local constructions of the(α,β)-metrics of constant flag curvature are still not clear,except for Randers metrics,Kropina metrics and square metrics.
For the discussions that follow, we need to clarify some notations for (α,β)-metrics. Let
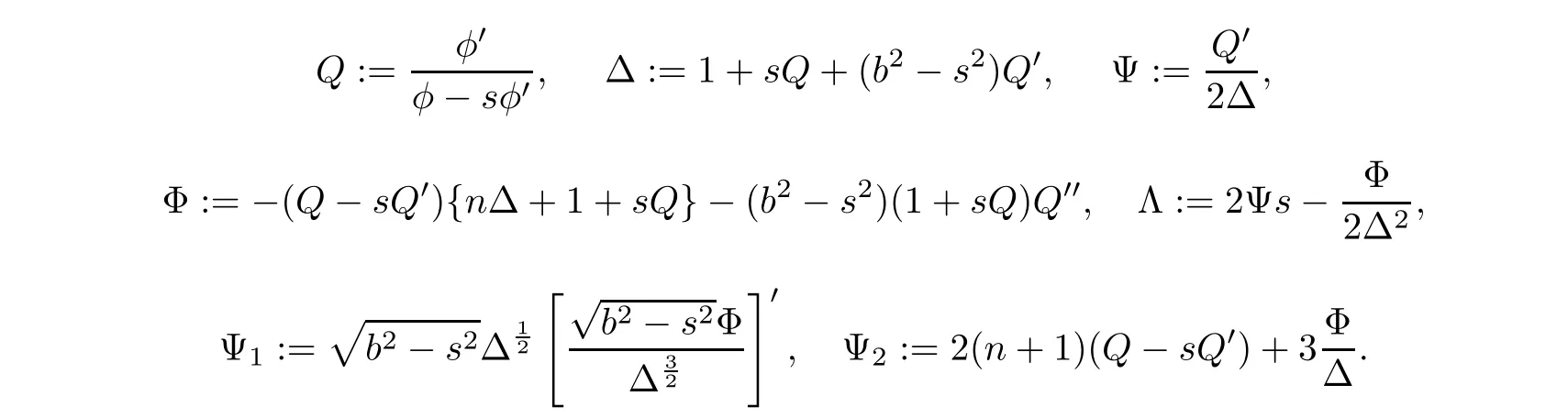
Furthermore, put
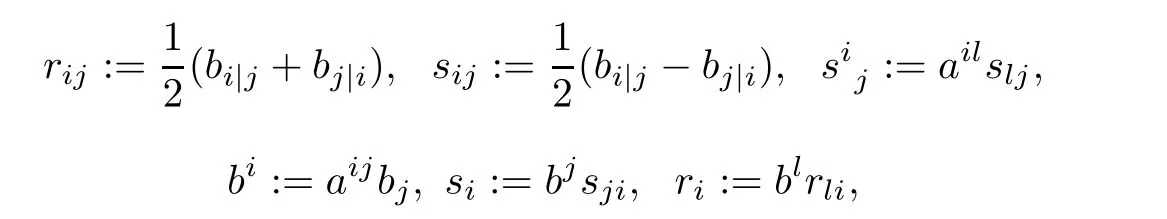
where“|”denotes the covariant derivative with respect to α. Let s0:=siyi, si0:=sijyj, r00:=rijyiyj, etc.. We say that β is a homothetic 1-form with respect to α if rij= caij, where c is a constant. We say that β is a Killing 1-form with respect to α if c=0. When c/=0, we have the following theorem:
Theorem 1.1 Let F =αφ(β/α) be an almost regular (α,β)-metric of non-Randers type on a manifold M. Suppose that β is a homothetic 1-form with respect to α satisfying that
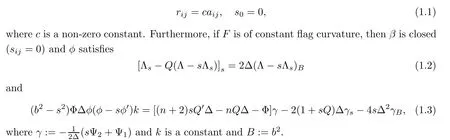
It is easy to see that b= constant if and only if ri+si=0. If rij=0 and si=0, then β is a Killing 1-form with constant length. In this case, we have the following result:
Theorem 1.2 Let F = αφ(β/α) be a regular (α,β)-metric of non-Randers type on a manifold M. Suppose that F is of constant flag curvature and that β is a Killing 1-form with constant length. Then F must be a locally Minkowskian.
From the proof of Theorem 1.2, the following is obvious:
Corollary 1.3 Let F = αφ(β/α) be a regular (α,β)-metric on a manifold M. Suppose that F is of constant flag curvature and that β is a Killing 1-form with constant length. Then F must be a Riemannian metric or locally Minkowskian.
2 Preliminaries
Let F be a Finsler metric on an n-dimensional manifold M. The geodesic coefficients Giof F are defined by ([5])

According to Deicke’s theorem, a Finsler metric is Riemannian if and only if the mean Cartan torsion vanishes ([10]).
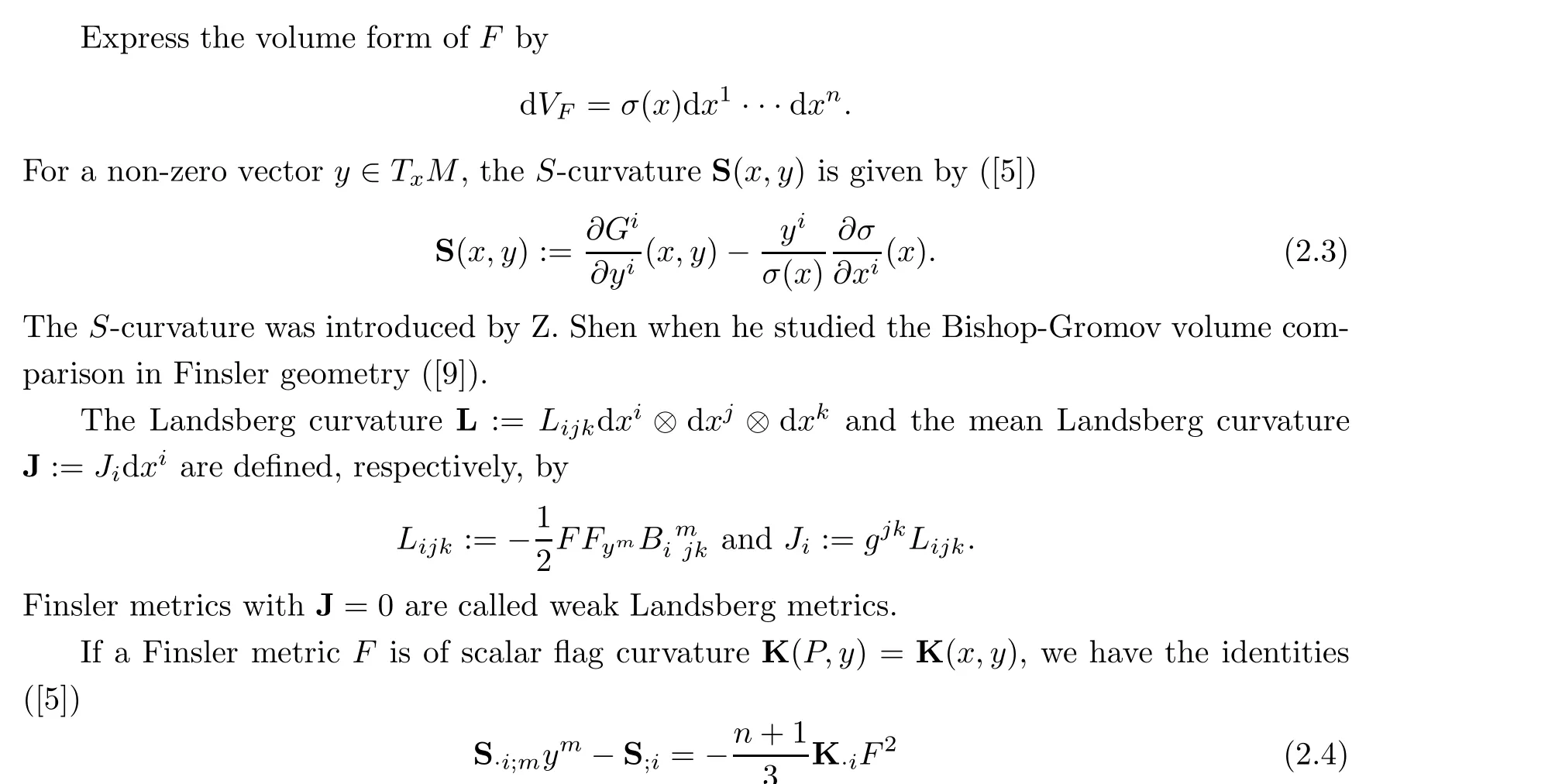
and


By a direct computation, we can obtain the following formula about the mean Cartan torsion of (α,β)-metric F ([4]):

3 The Discussions About Equation (2.4)
When a Finsler metric F is of constant flag curvature K, (2.4) becomes


Now we assume that β is a homothetic 1-form,that is,that rij=caij,where c is a constant,so

Then, by (3.6)-(3.12), we have the following result:
Proposition 3.1 Let F = αφ(β/α) be an almost regular (α,β)-metric of constant flag curvature. Suppose that β is a homothetic 1-form with rij=caij. Then it holds that

Plugging (3.10), (3.12), (3.19) and (3.18) into (3.6) and by using the Maple program, we can get (3.13) easily. □
4 Discussion of Equation (2.12)
Let F = αφ(β/α) be an (α,β)-metric on a manifold M. Suppose that β is a homothetic 1-form, that is, rij=caij, where c is a constant. It follows from (2.7), (2.10) and (2.11) that


When F is of constant flag curvature K, then substituting (4.3)-(4.7) into (2.12), we can get the following proposition:
Proposition 4.1 Let F =αφ(β/α)be an almost regular(α,β)-metric with a homothetic 1-form β on a manifold M. If F is of constant flag curvature, then it holds that
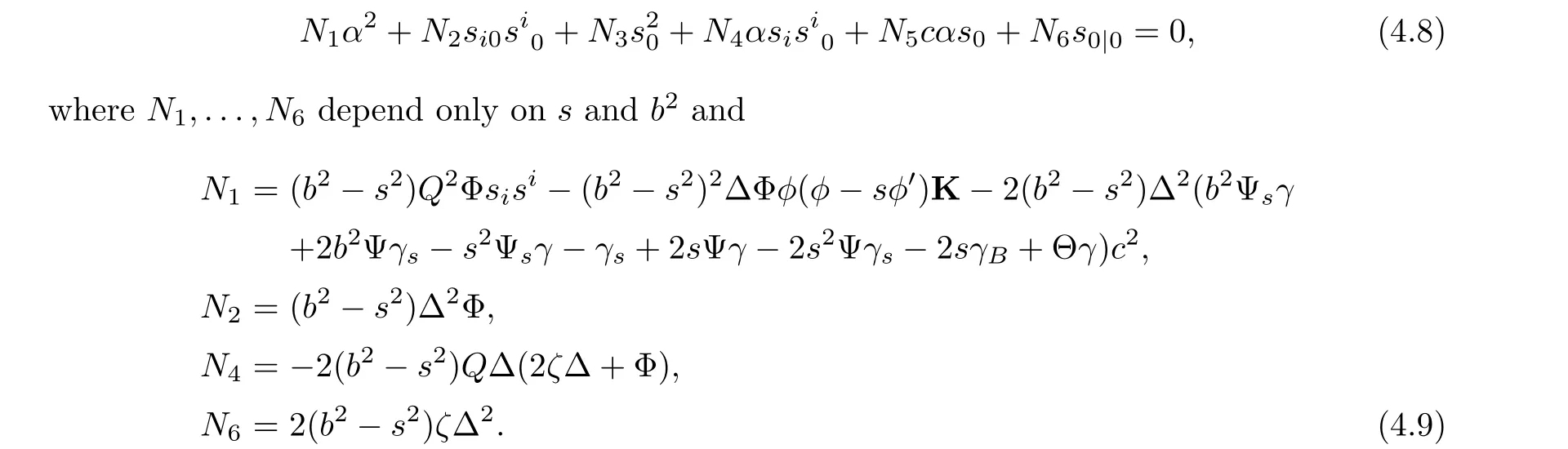
5 Proof of Theorem 1.1
First, we will give some necessary lemmas.
Lemma 5.1 Let F = αφ(β/α) be an (α,β)-metric of non-Randers type on a manifold M. If φ=φ(s) satisfies that

where C1and C2are constant.
Furthermore, we have the following lemma:
Lemma 5.3 Let F = αφ(β/α) be an almost regular (α,β)-metric of non-Randers type on a manifold M. Suppose that
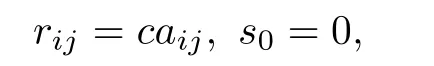
where c is a non-zero constant. If F is of constant flag curvature,then β is closed and φ satisfies that

which implies that Λ = k(B)φ. It follows from (5.9) and Lemma 5.2 that [k(B)]B= 0, which implies that k(B) is a constant. By Lemma 5.1, we get r0+s0=0, which contradict the fact that c/=0. Thus sQΛs+Λs-QΛ/=0. Then (5.10) implies that sij=0. □
Now we are in the position to prove Theorem 1.1. Under the conditions of Theorem 1.1,by Lemma 5.3, equation (1.2) holds and β is closed. Thus we only need to prove that equation(1.3) holds.


6 Proof of Theorem 1.2


which contradicts the assumption by Lemma 6.1. Thus K = 0. It follows from (6.4) that si0si0=0, that is, that aijsi0sj0=0. Then we have sij=0. In this case, rij=sij=0, which implies, by (2.7), that F is a Berwald metric. Hence F is locally Minkowskian. □
7 An Example
Usually, it is difficult to solve (1.2). In this section, we will determine the solution of(1.2) under the condition that Λ=f(s)g(B), where f(s) and g(B) are non-constant functions depending only on s and B, respectively.
First, when Q'=0, it is easy to check that



where λ is a non-zero constant and a=(ai) is a constant vector in Rn. In this case,
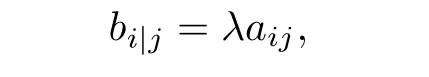
which means that (1.1) holds. Furthermore, we can check that φ=1/s satisfies equation(1.2).In fact, it is easy to see that φ = 1/s also satisfies equation (1.3) with k = 0. The metric F = α2/β is called a Kropina metric. The Kropina metrics of constant flag curvature have been classified in [8].
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- IMPULSIVE EXPONENTIAL SYNCHRONIZATIONOF FRACTIONAL-ORDER COMPLEX DYNAMICALNETWORKS WITH DERIVATIVE COUPLINGS VIAFEEDBACK CONTROL BASED ON DISCRETE TIME STATE OBSERVATIONS*
- GLOBAL SOLUTIONS TO A 3D AXISYMMETRIC COMPRESSIBLE NAVIER-STOKES SYSTEMWITH DENSITY-DEPENDENT VISCOSITY*
- COMPLETE MONOTONICITY FOR A NEW RATIO OF FINITELY MANY GAMMA FUNCTIONS*
- A NONSMOOTH THEORY FOR A LOGARITHMIC ELLIPTIC EQUATION WITH SINGULAR NONLINEARITY*
- UNDERSTANDING SCHUBERT'S BOOK (III)*
- a-LIMIT SETS AND LYAPUNOV FUNCTION FORMAPS WITH ONE TOPOLOGICAL ATTRACTOR *
