ON THE BOUNDS OF THE PERIMETER OF AN ELLIPSE*
2023-01-09TiehongZHAO赵铁洪
Tiehong ZHAO(赵铁洪)
Department of Mathematics,Hangzhou Normal University,Hangzhou 311121,China E-mail: tiehong.zhao@hznu.edu.cn
Miaokun WANG(王淼坤)Yuming CHU(褚玉明)
Department of Mathematics,Huzhou University,Huzhou 313000,China E-mail :wmk000@126.com; chuuming2005@126.com


The complete elliptic integrals and the Gaussian hypergeometric function play a very important and basic role in many branches of modern mathematics, including classical analysis,number theory,geometric function theory,and conformal and quasi-conformal mappings[9-23].Recently,the complete elliptic integrals have attracted the attention of many researchers on account of their extreme importance. We note that many remarkable monotonicity and convexity properties, as well as inequalities for K (r) and E(r), can be found in the literature [24-47].
In what follows, we denote by
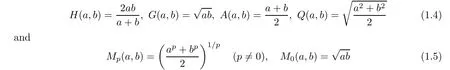
the harmonic,geometric, arithmetic, quadratic, and p-th power means of two positive numbers a and b, respectively.
In recent decades, the bounds and approximate formulae for the perimeter of an ellipse have attracted the attention of many researchers [48-56].
Vuorinen, in [57], conjectured that

In their latest paper[62],the authors improved upon the lower and upper bounds for L(a,b)by using the convex combination of the lower bound in (1.6) and the upper bound in (1.7).More precisely, they showed that the double inequality

which is used to provide new bounds for the perimeter of an ellipse L(a,b).
2 Lemmas
In order to prove our main results, we need several formulae and lemmas, and we present them in this section.

be a convergent power series on the interval (0,r) (r > 0). Then the following statements are true:
(1) If S(r-)≥0, then S(x)>0 for all x ∈(0,r).
(2) If S(r-)<0, then there is a unique x0∈(0,r) such that S(x)>0 for x ∈(0,x0) and S(x)<0 for x ∈(x0,r).
Lemma 2.2 (See [64]) We have the double inequality




where cnis defined as in Lemma 2.4.

On the other hand, it is clear that c3= (3-32λ)/256. Lemma 2.4(1) and (4) lead to the conclusion that

3 Main Results
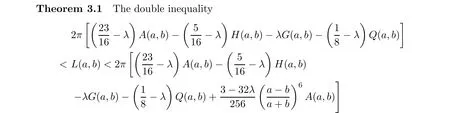
holds for all a,b>0 with a/=b, where λ is defined as in (1.11).
Proof Since L(a,b) and A(a,b),H(a,b),G(a,b),Q(a,b) are symmetric and homogeneous of degree one, without loss of generality, we assume that a >b>0 with b/a=(1-r)/(1+r)for r ∈(0,1). Then it follows from (1.1), (1.4), (1.5) and the Landau identity (2.1) that




It is easy to see that ∊(r) is strictly increasing on(0,1). Actually, the absolute error is less than∊(3/4)=7.42011×10-7on (0,3/4], which is better than that given in [62, Remark 3.5].
猜你喜欢
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- IMPULSIVE EXPONENTIAL SYNCHRONIZATIONOF FRACTIONAL-ORDER COMPLEX DYNAMICALNETWORKS WITH DERIVATIVE COUPLINGS VIAFEEDBACK CONTROL BASED ON DISCRETE TIME STATE OBSERVATIONS*
- GLOBAL SOLUTIONS TO A 3D AXISYMMETRIC COMPRESSIBLE NAVIER-STOKES SYSTEMWITH DENSITY-DEPENDENT VISCOSITY*
- COMPLETE MONOTONICITY FOR A NEW RATIO OF FINITELY MANY GAMMA FUNCTIONS*
- A NONSMOOTH THEORY FOR A LOGARITHMIC ELLIPTIC EQUATION WITH SINGULAR NONLINEARITY*
- UNDERSTANDING SCHUBERT'S BOOK (III)*
- a-LIMIT SETS AND LYAPUNOV FUNCTION FORMAPS WITH ONE TOPOLOGICAL ATTRACTOR *
