基于NARX神经网络的车用锂离子电池SOH时间序列预测

徐东辉，石本改，徐丽琴，叶雪强，王丽娜

(1.南昌师范学院数学与计算机科学系，江西 南昌 330032；2.广东机电职业技术学院汽车学院，广东 广州 510550； 3.长沙理工大学汽车与机械工程学院，湖南 长沙 410076)

锂电池具有环保、比能量大及无记忆效应等诸多优点，目前锂离子电池广泛应用于新能源电动汽车[1]。然而锂离子电池在使用中受其健康状态(SOH)、功率状态(SOP)及荷电状态(SOC)等影响，有时会导致灾难性的事故发生，因此精确预测SOH、SOC等状态量对于提高锂离子动力电池的使用安全性具有重大的现实意义[2-3]。

目前针对SOH的研究主要为数据驱动方法。徐元中等[4]针对BP网络权值存在局部最优的缺陷，采用模拟退火算法(SA)优化BP权值，使其达到全局最优，通过试验仿真有效验证了该算法可以有效提高锂离子动力电池的SOH预测精度。张任等[5]提出了基于粒子群优化RBF神经网络的预测算法，建立了电池的热力学模型和等效电路模型，提取影响锂离子电池SOH的关键参数，并对关键参数进行在线实时辨识，结果显示预测精度比BP神经网络提高了20%，时间也节省66.7%以上。潘海鸿等[6]通过构建表征电池性能衰退的健康指标(HI)，用极限学习机算法对健康指标进行训练和预测,实现了SOH的在线预测，并且预测误差没有超过2%。

上述SOH的算法在预测精度上都得到了有效提高，但很少从锂电池系统本身固有的非线性动力学混沌特性方面开展研究，并且所用到的数据样本大多为一维状态空间的时间序列或者单变量数据样本，数据样本包含的信息比较单一，不够全面。为此本研究针对锂离子电池SOH时间序列非线性特性，提出了基于NARX神经网络的预测模型，通过对锂电池系统的混沌动力学进行判定，利用相空间重构技术对试验采集到的一维状态空间的时间序列数据进行重构，恢复锂电池系统本身的混沌动力学特性属性，然后利用NARX神经网络对重构后的时间序列数据进行训练和预测，最后通过仿真试验验证了基于NARX神经网络预测模型的有效性。

1 锂离子动力电池系统混沌判别

要将混沌时间序列分析法应用于锂离子动力电池系统SOH时间序列预测中，首先要判断锂离子动力电池系统SOH时间序列是否为混沌时间序列，判别方法有K熵法及关联维D2法等[7]，本研究采用关联维D2法判别。

在所考察的m维相空间中设相点之间的欧氏距离为rij(m)：

rij(m)=‖Xm(ti)-Xm(tj)‖。

(1)

假设任给定一标度r，则统计相点之间欧氏距离小于r的点对数目在所有相点之间点对数目中所占的比例为

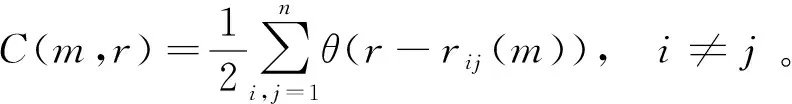
(2)

式中：n为相点数；θ为Heaviside函数。

关联维D(m)记为

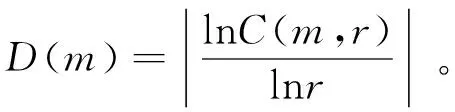
(3)

式(3)不随m改变，于是得到锂离子电池系统的关联维数：

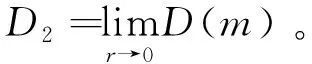
(4)

依据式(4)，可计算锂离子电池系统的关联维数为D2>2.3，表明锂离子电池系统具有混沌特性，则该锂离子电池系统吸引子的维数为D2，可对锂离子电池系统SOH时间序列进行预测。

2 多变量时间序列重构

在混沌理论中单变量时间序列和多变量时间序列的预测原理都是相空间重构理论，而在一定程度上，单变量时间序列可以认为是多变量时间序列的一种特例，因此可以将单变量时间序列的延时重构用于多变量时间序列中[8]。

对于锂离子电池，假设SOH的时间序列为{x(i),i=1,2,…N}，根据Takens理论[9-10]，若时间延迟τ和嵌入维数m具有确定值时，则锂离子电池健康状态(SOH)时间序列相空间相点可表示为

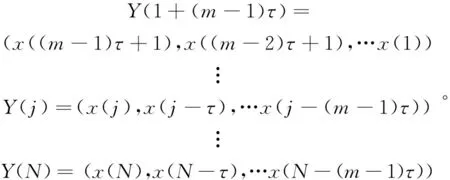
(5)

式中：m为嵌入维数；τ为时间延迟。

Y(j)为相空间中的点，相点总数M满足条件：

M=N-(m-1)τ。

(6)

假设X1,X2,…XN为M维多变量时间序列，其中任意时间序列可表示为Xi=(x1,i,x2,i,…xm,i)，(i=1,2,…N)，由此可知，当M=1时为单变量序列。

因此，延迟相空间重构相点如下：

Vn=(x1,n,x2,n-τ,…,x1,n-(m1-1)τ,…,
xM,n,xM,n-τM,…,xM,n-(mM-1)τM)。

(7)

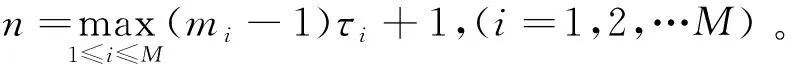
x1,i+1=Φ1(Vi),x2,i+1=
Φ2(Vi),…,xM,i+1=ΦM(Vi)。

(8)

τ和m的选取对于相空间重构非常重要，为此Kim等于1999年提出了用于计算τ和m两个参数的C-C方法。由于C-C方法具有操作方便、易实现及抗噪强等特点,并且对于小数据样本具有较好的可靠性，因此选择C-C方法计算τ及m相空间重构两个重要参数。

为方便计算，假定τs为锂离子电池系统试验数据采集时间间隔，τd=tτs为延迟时间，τw=(m-1)τd为延迟时间窗口，τp为平均轨道周期(τw≥τp)。

C-C方法的具体步骤如下。

1) 计算锂离子电池系统给定时间序列的标准差σ。

2) 通过下式可得S(t),ΔS(t)及Scor(t)3个变量的值：

(9)

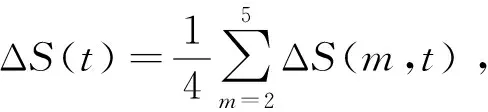
(10)

(11)

3) 依据ΔS(t)的第一个极小值，寻找时间序列独立的第一个局部最大值，通过τd=τs可得第一个局部最大时间。

同理，用SCOR(t)的最小值寻找时间序列独立的第一个整体最大值时间窗口τw=τs。

利用上述3个步骤计算可得τ=3，m=8，利用此结果对采集到的一维SOH数据样本进行相空间重构，将锂电池系统恢复成8维非线性状态空间，进而呈现出锂电池系统固有的多维非线性状态空间。

3 基于NARX神经网络的预测模型建立

3.1 NARX神经网络

NARX神经网络是一种非线性自回归神经网络，具有动态反馈性，即其输出结果是当前外部输入和历史输出结果的非线性函数，由于网络结构中存在时延以及反馈，因此NARX神经网络具有记忆和联想功能以及较强的适应能力，很适合用于非线性时间序列的预测[11-12]。NARX网络模型可表示如下：

y(t)=f(y(t-1),y(t-2),…y(t-ny),
u(t-1),u(t-2),…u(t-nu))。

(12)

式中：y(t)为目标向量；u(t)为外部输入向量；f为非线性函数；y(t-1),y(t-2),…y(t-ny)为时延后的期望目标向量；u(t-1),u(t-2),…u(t-nu)为时延后的外部输入向量。

NARX神经网络的隐层激活函数f1和输出层激活函数f2分别表示如下：

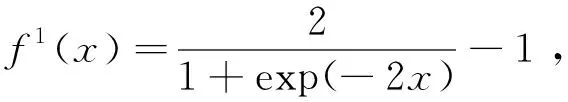
(13)

f2(x)=x。

(14)

NARX神经网络训练采用的是Levenberg-Marquards算法，假设一个最大位移作为区域半径，然后在该区域内寻找代价函数的极小值点，若目标代价函数值增大，则调整该区域半径改变范围，继续求解；若目标代价函数值减小，则继续迭代计算[13-15]。

为了评价NARX神经网络模型的模拟性能，采用以下3种误差模型对NARX模型进行指标评价：平均绝对误差(MAE)、均方根误差(RMS)及平均相对误差(MSE)，表达式如下：

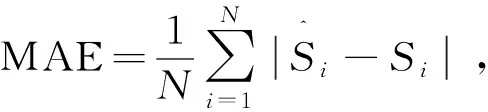
(15)

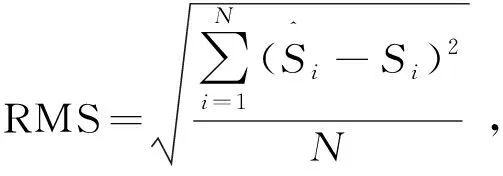
(16)

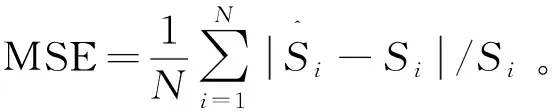
(17)

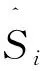
3.2 预测模型建立

本研究提出基于NARX神经网络的建模方法，对输入变量进行相重构空间恢复系统的多维非线性状态空间时间序列，并将其输入NARX神经网络，获得最终的SOH预测值。按上述原理建立基于NARX神经网络的预测模型，其结构如图1。

图1 NARX的预测模型结构NARX预测模型算法实现的过程如下。

步骤1：采用灰色关联从自主试验平台锂离子电池退化状态监测到的数据中选择NARX预测模型的输入变量。

步骤2：采用C-C法确定嵌入维数m和时间延迟τ两个相空间重构中重要的参数，经计算最后确定τ=3,m=8。将上述结果应用于对试验采集到的一维试验数据重构中，由此可假定NARX预测模型的训练样本集为{xi,yi}，xi∈RN×M,yi∈RN×L，测试样本集为{xt,yt}，xt∈RN×M,yt∈RN×L。

步骤3：利用重构后的训练样本集{xi,yi}，xi∈RN×M,yi∈RN×L训练NARX模型，利用测试样本集{xt,yt}，xt∈RN×M,yt∈RN×L对 NARX模型进行预测，得到最终的SOH输出值。

4 试验与分析

在试验过程中使用的试验数据集主要是通过官网下载到的NASA PCoE研究中心在爱达荷州国家试验室测试获得的B5和B6电池各168组数据。自主试验过程中选用2个额定容量为2 A·h的18650型号的锂离子电池(B5和B6)为研究对象，在常温(25 ℃)条件下，完成锂离子电池(B5和B6)的充电、放电和电阻测量等试验。

充电试验：先以1C(2 A)恒流进行充电，当锂离子电池(B5和B6)的电压达到4.2 V时，再以恒压充电，直到I≤20 mA时停止充电，在试验过程中实时记录电池终端电压、电流、温度、充电器电压及电流等数据。

放电试验：先以2 A恒流放电，当电池B5和B6的电压分别降至2.7 V和2.5 V时，停止放电。在试验过程中实时记录电池终端电压、电流、温度、充电器电压及电流等数据。

重复上述充放电试验直到电池的实际容量下降到额定容量的70%，停止老化试验。

以上充放电操作一次记为一次循环过程，整个试验共完成200次循环，试验过程中数据的采用频率设置为1 Hz，实时同步采集电池终端电压、输出电流、温度、充电器电压和电流、时间等数据，并且同时记录B5和B6电池的最大可用容量。采用EIS方法获取电池阻抗，频率扫描范围为0.1～5 Hz。

相空间重构自主试验平台采集电池退化状态数据，将重构后的电池退化状态数据中的前80组数据与NASA PCoE研究中心的B5电池前80组数据一起作为NARX神经网络的训练集。取上述相空间重构获得的数据中的后88组数据与NASA PCoE研究中心的锂离子电池B5后88组数据一起作为NARX神经网络的测试集，B5电池的失效阈值为0.727 4。图2示出锂离子电池B5的SOH预测结果，图3示出B5预测结果相对误差。

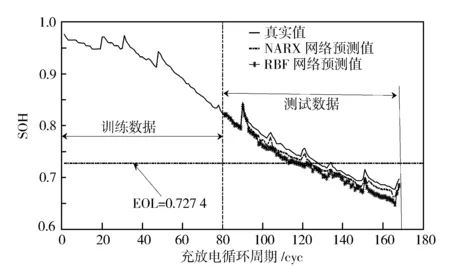
图2 锂离子电池B5的SOH预测结果

图3 锂离子电池B5的SOH预测结果相对误差

同理，选取B6电池前60组数据及利用自主试验平台锂离子电池退化状态监测到的数据，通过相空间重构后得到的前60组数据一起作为NARX神经网络的训练集。同样取上述相空间重构获得的数据中的后108组数据与NASA PCoE研究中心的B6电池后108组数据一起作为NARX神经网络的测试集，B6电池的失效阈值设置为0.68。由于对采集到的试验数据重构后得到8维的时间序列数据，因此RBF神经网络模型输入层选择为8个神经元，通过不断试验最终确定中间层神经元个数为16个，输出层为1个。最终确定RBF神经网络模型为8-16-1结构形式。图4示出锂离子电池B6的SOH预测结果。

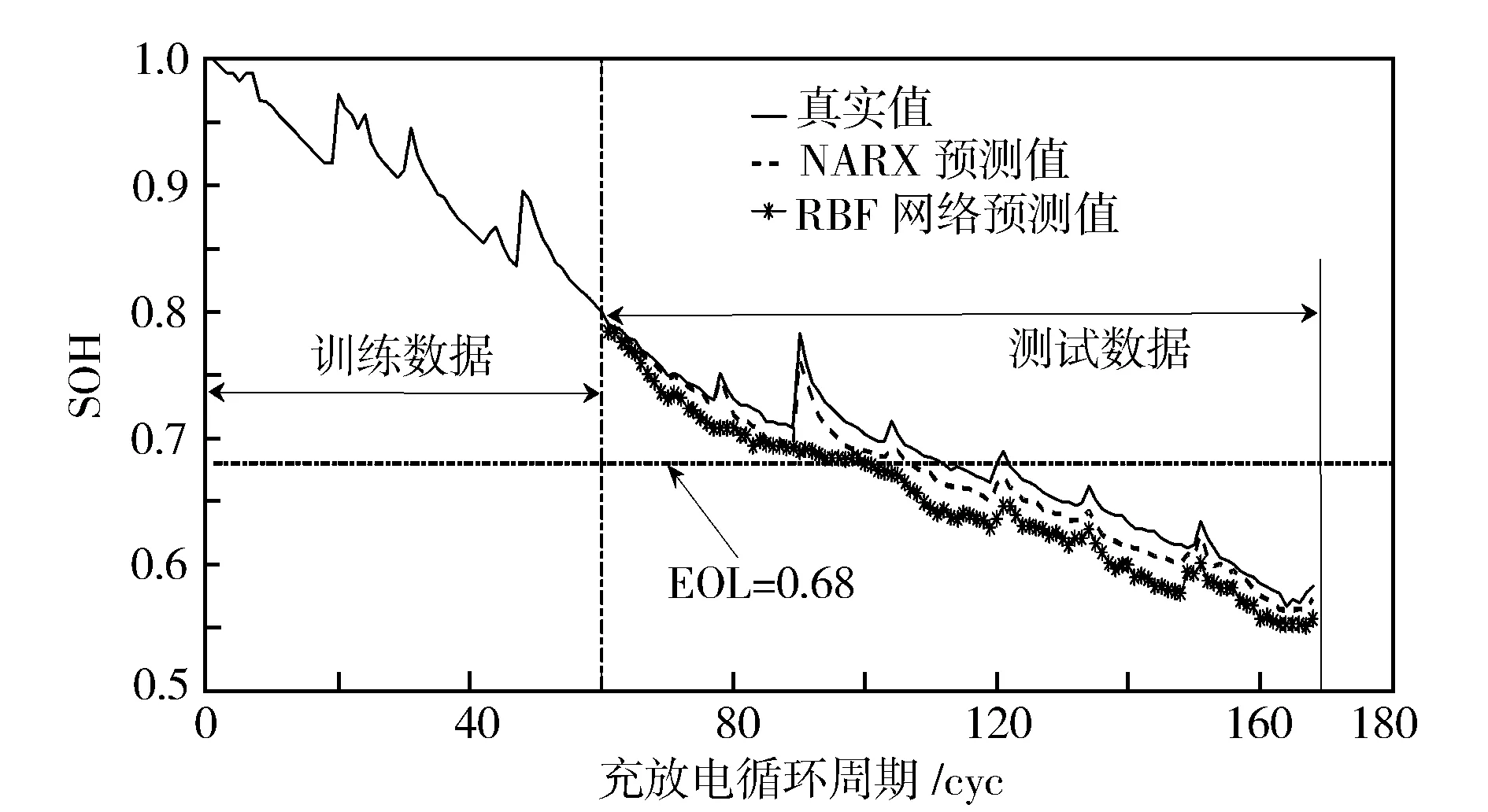
图4 锂离子电池B6的SOH预测结果

通过表1的SOH预测结果对比，可知NARX模型比RBF模型的SOH预测值平均相对误差提高了2个百分点，均方根误差提高了近6个百分点。进一步说明了本研究提出的NARX模型具有较高的精确度及稳定性，更强的非线性预测能力。

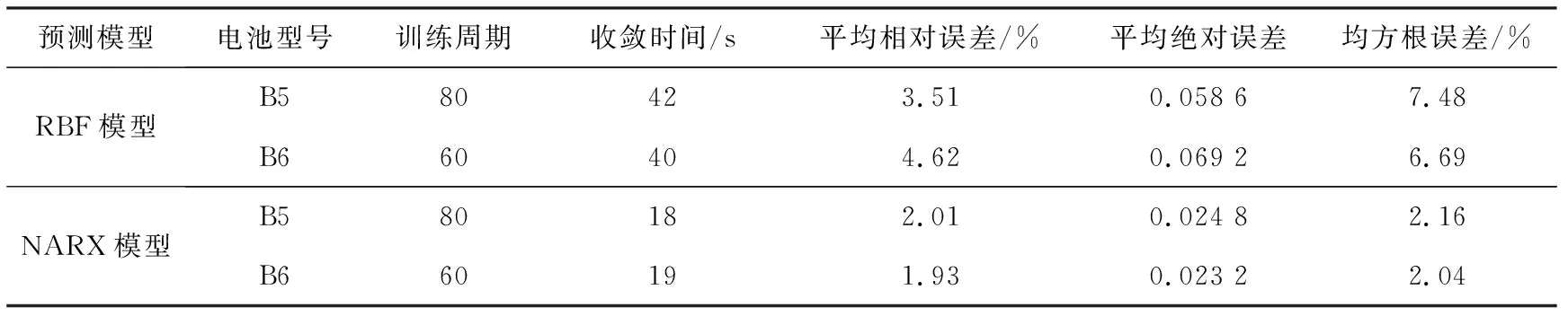
表1 锂离子电池B5及B6的SOH预测误差对比

5 结束语

锂离子电池系统各参数具有慢时变特性，准确预测健康状态存在较大的难题，提出了NARX神经网络预测模型，用于对非线性状态下的锂离子电池SOH时间序列的预测。

通过混沌判别表明了锂离子电池系统具有混沌特性，采用相空间重构技术恢复了锂离子电池系统固有的多维非线性状态空间，最后利用重构后得到的数据对NARX模型进行了训练和测试。

通过仿真结果可知NARX模型算法的SOH预测结果的相对误差比RBF网络提高了近6个百分点。表明了本研究提出的基于NARX神经网络的SOH预测算法具有较高的预测精度，相空间重构技术有利于提高NARX模型的预测精度。