基于改进方差法的压气机喘振在线检测
2023-01-09陈明张志强
陈明,张志强
(北京理工大学机械与车辆学院,北京 100081)
随着人们对汽车动力性和经济性的要求不断提高,涡轮增压技术被广泛应用于汽车。但压气机发生喘振后性能会大大降低,造成发动机进气管内压力波动大,影响其动力输出,同时引起增压器中零部件的损坏。喘振是增压器危害最严重、破坏最大的一类故障[1],准确预测喘振并防止其发生可以有效避免设备工作在较差的工况,减小增压器损坏的概率[2]。
很多学者在研究喘振现象时重点分析了喘振发生过程中所涉及到的物理现象,如压力、温度、声音等热力或气动参数的幅值会发生剧烈变化[3-4],并将稳态到喘振整个过程的频谱绘制成云图来查看相关物理量的变化趋势。
当出现喘振时,由于压气机出口压力变化明显,压力传感器响应速度快,适合用来检测喘振[5]。对于压力信号的处理,谢锋[6]对检测到的压气机数据进行小波降噪处理,当重构信号的幅值超过阈值时认为发生失速;严潇[7]在匹配滤波后统计移动时间窗内波动数量来进行实时判别喘振;薛翔[8]通过分析在盖板处安装的多个压力传感器采集到的数据提出一种基于混沌特性的判断指标;王玉东[9]通过检测压气机出口静压的一阶和二阶变化率检测喘振是否发生。若从能量的角度来考虑,李长征[10]、张靖煊[11]、朱智富[12]研究发现在进入喘振状态过程中,压气机出口总压脉动增大,使得短时能量或方差明显增大,采用该方法可较准确地判断喘振是否发生。
压气机喘振对设备性能影响大,且喘振信号特征复杂,即使同一型号压气机在不同工况、不同安装方式下其喘振信号特征也不相同,如何能够快速准确地识别喘振工况一直是研究者追求的目标。本研究针对涡轮增压器离心压气机的喘振检测,采用了一种基于改进方差法的压气机喘振识别方法,对该方法的实时检测速度和适应性进行了研究。
1 喘振试验及数据分析
采用JP60涡轮增压器为研究对象,对其进行逼喘试验,试验台原理如图1所示。本次试验采用冷吹法,调节阀门F1使增压器转速维持在60 000 r/min,压气机出口压力信号采样频率为100 Hz。
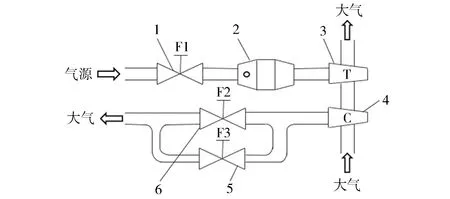
1—涡轮进气控制阀; 2—燃烧室; 3—涡轮; 4—压气机; 5—压气机放气微调阀; 6—压气机放气阀。 图1 压气机性能试验台原理
试验过程中,当增压器在稳态工况下稳定一段时间后,逐渐减小阀门F2开度,待接近喘振时保持阀门F2开度不变,逐渐减小阀门F3开度,直至达到喘振,压气机出口动态压力信号如图2所示。
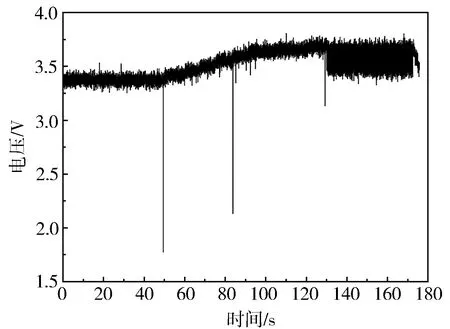
图2 压气机出口动态压力信号
由于稳态工况及调节过程数据量大,为便于分析,图3中仅保留了喘振前5 s的数据。由图3可以看出,检测信号包含高频噪声且压气机在4.28 s处由于外部电磁干扰,采集到的信号出现奇异点。在5 s处压气机发生喘振,此时采集到的压力信号出现低频较大幅值的波动,且呈现一定周期性。

图3 压气机喘振点附近信号
对采集到的数据进行频谱分析,图4中展示了随着时间的推移,压气机流量不断减小,各个时间段内的频谱分析结果。在最初的时刻,压气机处于稳态工况,采样信号呈现均值不为0的连续频谱。当发生喘振后,信号能量集中在4.4 Hz左右,幅值从稳态工况时的小于0.02增加到0.1。
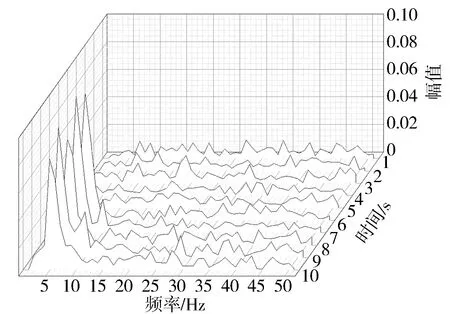
图4 稳态到喘振过程频谱分析
图5示出信号出现奇异点处放大后的波形,可见当出现外部干扰后,采集到的数据突然减小,随后恢复到稳态值,类似于脉冲信号。奇异点的出现极大地影响了对喘振信号的检测,因此在进行喘振识别之前必须先检测出信号的奇异点并将其去除。
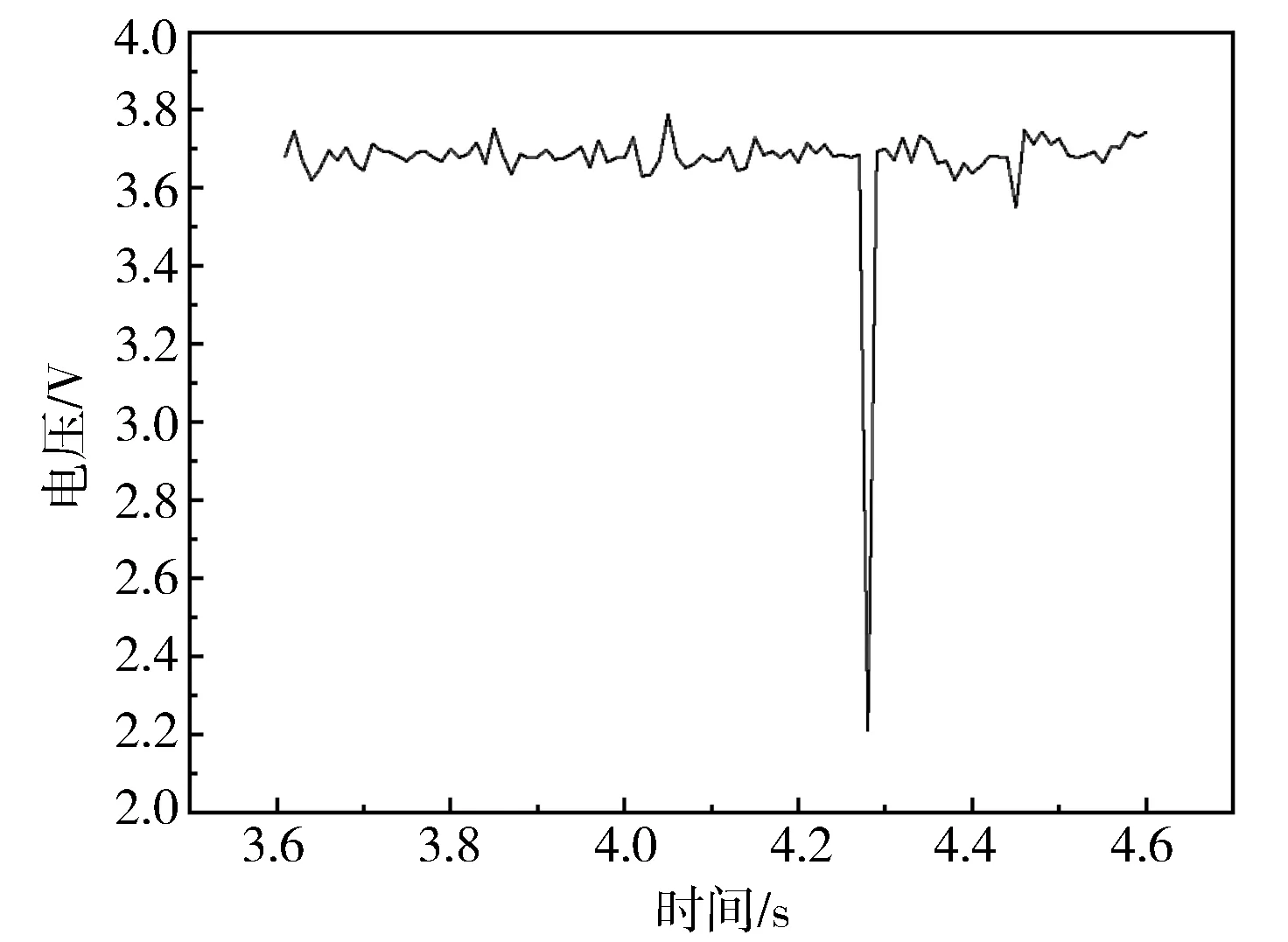
图5 数据采集过程中的奇异点
2 喘振信号奇异点检测及滤波
2.1 信号奇异性分析及检测
小波变换具有空间局部化性质,信号在某点附近的局部信息完全确定了该点在小尺度下的小波变换[13],能更好地分析奇异点的位置及奇异性的强弱。
2.1.1 奇异点位置的确定
小波函数随着消失矩增大在频域内会表现更好的局部性、更高的分辨率,但同时会造成支撑也更大,导致在奇异点检测时滞后性增大并带来不必要的计算量。因此,为满足喘振检测实时性要求,选择haar小波作为小波基。
此时小波函数及待分析信号f均为实函数,设尺度参数s>0,θ(t)是一个光滑函数,小波ψ(t)是θ(t)的一阶导数,则f的连续小波变换为
(1)
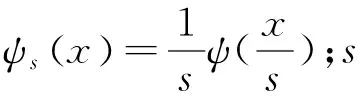
由式(1)可以看出,小波变换模极大值|Wf(s,x)|就是信号f经过单位脉冲响应为θs的系统后的一阶导数的极大值,恰好对应压气机出口压力信号的突变点。
压力信号f(t)被采样后,假设以离散方式{p1,p2,…pn}输入,在采集过程中实时对该信号进行二进小波分解,尺度为i=1~3,记录每层分解的小波系数,结果如图6所示。
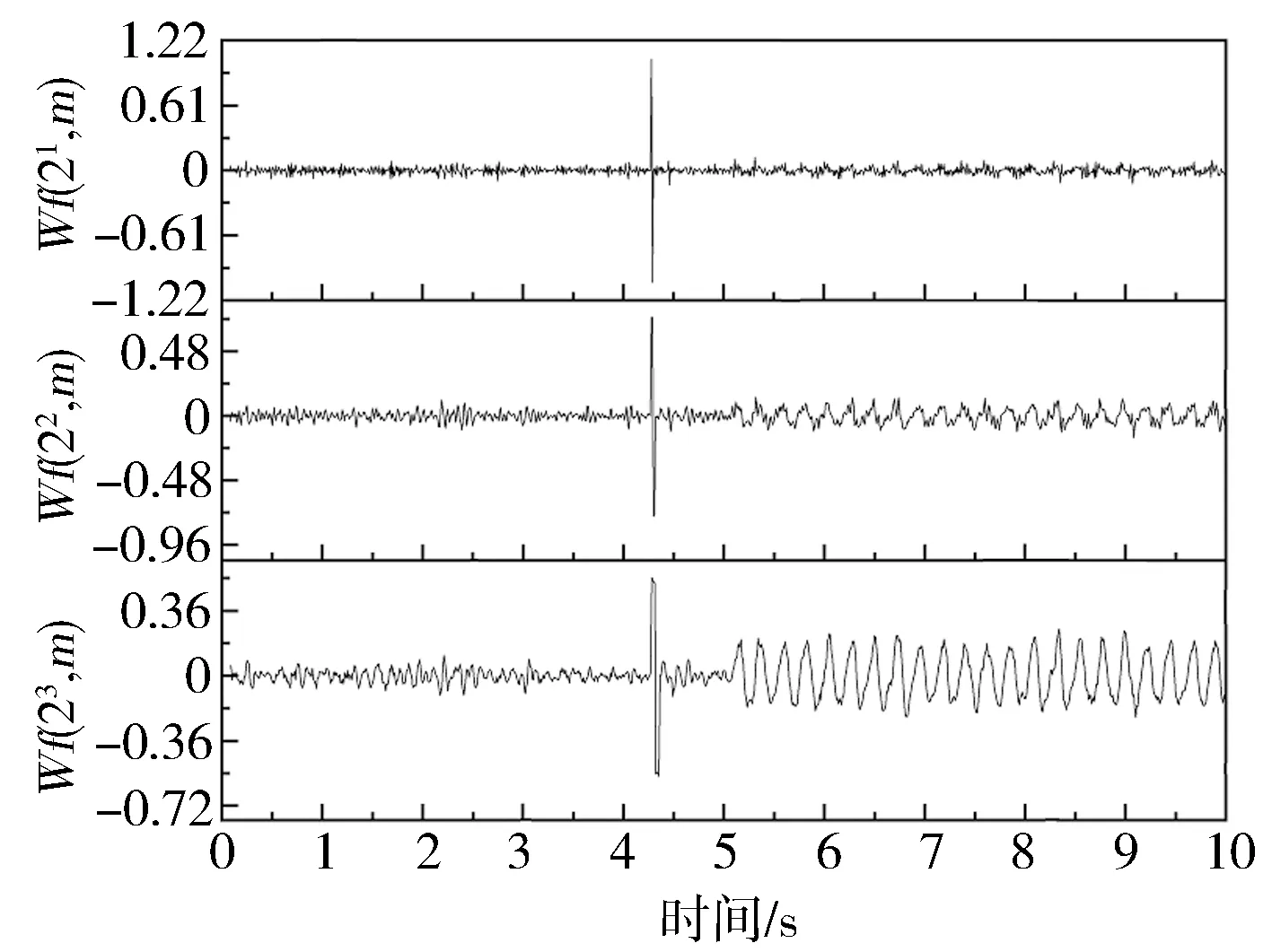
图6 压力信号3层haar小波分解
从图6及小波理论分析可知,尺度为21时噪声较多,对奇异点位置的确定造成干扰,故将22,23尺度上的模极大值提取出来用以确定奇异点的位置(见图7)。
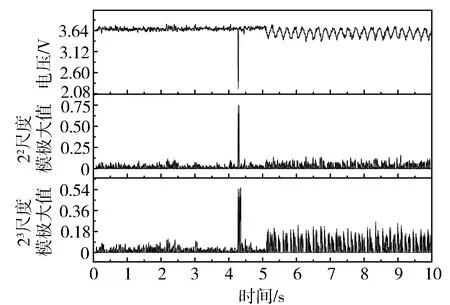
图7 压力信号及信号的模极大值
在图7中可以看到,模极大值位置与奇异点位置是同时出现的,由于小波分解是随着信号的采集实时进行,信号的一个奇异点可能对应着多个距离相近的模极大值,但第一次出现模极大值的时刻是相同的,可在该时刻计算奇异性。
2.1.2 信号奇异性度量
使用Lipschitz指数来度量采样信号的奇异性,对于二进尺度si和si+1,α计算公式为
(2)
由式(2)计算信号在4.21 s及尺度s2和s3下的α,结果为-0.432 7。Lipschitz指数在该时刻小于1,说明信号在该点是奇异的。
当奇异处是一个δ函数时,α=-1,表明该点的奇异性较严重。但由于小波函数的选择以及喘振信号奇异处的波形与δ函数存在差距,使得计算出来的α值达不到理想值-1,但计算结果在一定程度上也能够说明使用小波变换能够较好地检测出信号的奇异点。
2.2 小波滤波
在信号处理领域中,小波变换广泛应用于信号的滤波,具有很强的去数据相关性[14]。
喘振信号经过3层haar小波变换后,信号的能量集中在一些大的小波系数中,而噪声能量分布于整个小波域内,使得信号的小波系数幅值远大于噪声的系数幅值。保留大尺度低分辨率下的全部小波系数,对于其他尺度下的小波系数,设定阈值为0,即将21和22尺度下的小波系数置为0,而23尺度下的小波系数保留原来的数值,完成对小波系数的阈值处理。
将处理后的小波系数利用逆小波变换进行重构,恢复原始信号的估计值。去掉奇异值及小波滤波后的信号如图8所示,可以看出在使用小波滤波去噪后,高频分量大大减少,信号的信噪比得到提高。
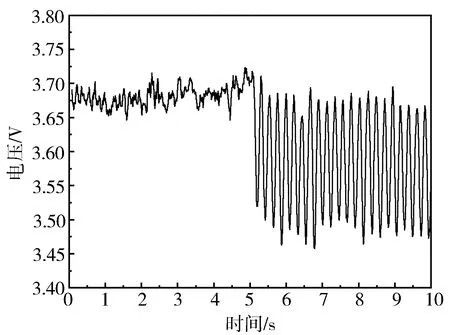
图8 去除奇异点及滤波后的信号
3 基于改进方差法的压气机喘振识别
3.1 改进方差法及分析
3.1.1 改进方差法
本研究分析了不同的支气管哮喘患儿血清RBP、IgE、IL-4水平及痰EOS水平变化,得出MP感染能够加重气道炎症反应,降低肺功能的结果,增加了国内外关于此方面的报道,但仍存在部分局限性:①样本量较小,科学性有限,后期仍需大样本随机对照研究进一步论证此结论;②对于不同感染程度的支气管哮喘患儿没有进一步研究,MP感染与血清RBP、IgE、IL-4水平变化仍需进一步论证。
经过对压气机出口动态压力信号分析及预处理,发现压气机在发生喘振后压力信号变化幅值急剧增大,且相关研究表明,不同的工况、型号都呈现出相似的情况[15-16]。针对该现象,统计一段时间内信号的方差是检测压气机喘振的一种有效方法,而方差可以认为是相对于均值的能量。考虑到信号经过采样系统后产生采样序列{p1,p2,…pn},在该序列中每一时刻对应着一个采样点,第n个采样点代表了压气机所在工况的当前状态,当出现喘振后其相对于之前采样值的变化更加明显,因此在试验时统计第n个采样值相对于前n-1个采样值的能量变化进行压气机喘振检测。
采样序列的方差为
(3)
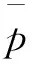
定义改进方差为第n个点相对于前n-1个点的差值平方和,其计算公式为
(4)
两种检测方法计算结果之差为
(5)

对比式(3)与式(4)发现,改进方差法与方差法均反映了信号在一段时间内的能量,但它们的区别在于改进方差法在计算时多了第n个采样值与平均采样值差的平方。在喘振检测时,由于稳态工况下在信号采集时受到噪声的干扰,采样值会发生小幅度波动,此时Δp较小,计算出来的改进方差数值与方差差别不大。但当压气机发生喘振后,|Δp|随着信号幅值的减小而增大,使得两种方法计算结果差值随之呈现二次增长的变化规律。
3.1.2 改进方差法计算结果影响因素分析
(6)
在稳态工况下,改进方差计算结果为
(7)
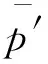
式(7)中等号右端第一项代表了压气机出口压力的波动;第二项为压气机出口压力信号与噪声信号的协方差,反映了两个随机变量之间线性程度,该值约等于0;第三项是由噪声引起的,为噪声的方差。假定第一项数值取为M1,第三项数值取为M2,设定检测阈值为K(M1+M2)(其中K为安全系数),当改进方差计算结果大于该阈值时判断喘振发生。采用该方法判断涡轮增压器压气机的喘振时,由于M2为噪声的方差,仅与检测系统相关,不受增压器型号或运行工况的影响,因此改进方差的计算结果仅与第一项压气机出口压力波动相关,而该波动程度主要受到气源波动幅度影响,对在同一检测装置检测压气机喘振具有良好的通用性。
3.2 仿真试验分析
根据采集到的压气机出口动态压力数据,利用改进方差法对压气机喘振行为进行仿真,结果如图9所示。从图中可见,压气机未发生喘振时改进方差法计算结果数值较小,发生喘振后该值突然增大,与稳态工况计算数值形成鲜明对比。观察图9中喘振初期采样信号与检测结果的部分放大图,对比可以发现,当喘振发生后,由于数据处理的滞后,改进方差计算值并不能立即反映出已经检测到喘振,需要等待0.1 s才能达到检测结果最大值。但若以0.005作为阈值,改进方差法可在喘振发生后0.07 s内进行喘振特征识别,检测时间小于半个喘振周期。
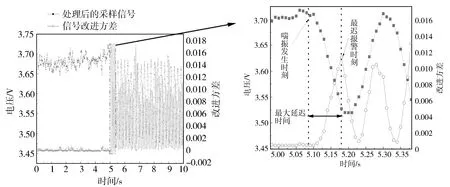
图9 改进方差法检测结果
图10a对比了方差和改进方差两种方法的计算结果,可以看出由方差计算得到的检测结果与改进方差法相比,检测滞后时间相同,而计算数值有所差别。二者差值如图10b所示,在未发生喘振时,两种方法差值在0附近波动,但发生喘振后差距增大,与理论分析一致。
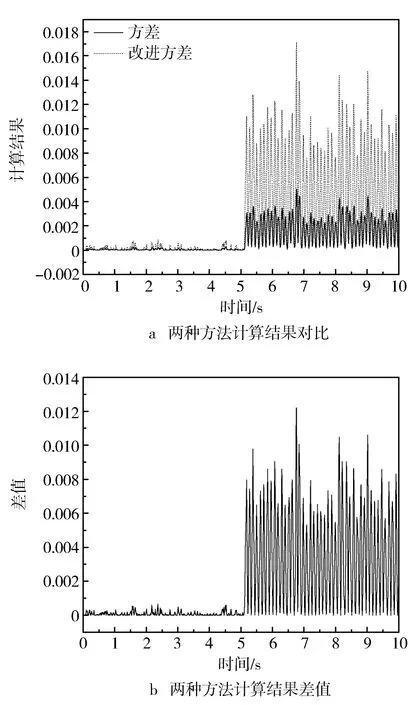
图10 方差法与改进方差法计算结果
对比两种方法在两种工况下计算结果最大值,如表1所示,其中喘振工况最大值为第一个喘振周期内的计算结果最大值,对比两者可以发现改进方差法在对计算结果放大的同时将信噪比提高了20.5%,提高了检测结果的准确性。

表1 两种方法在不同工况下最大值对比
3.3 不同工况及不同型号压气机喘振检测验证分析
对JP60在100 000 r/min和JP90在60 000 r/min下的压力信号进行分析,检测阈值与JP60在60 000 r/min工况相同,结果如图11和图12所示。从图11和图12中可以看出,改进方差法对于不同型号和工况的压气机均在半个喘振周期内检测到喘振的发生,具有较好的实时性和通用性。由图12还可以看出,检测时计算结果在进入深度喘振前就超过阈值,可提前检测到压气机喘振现象。
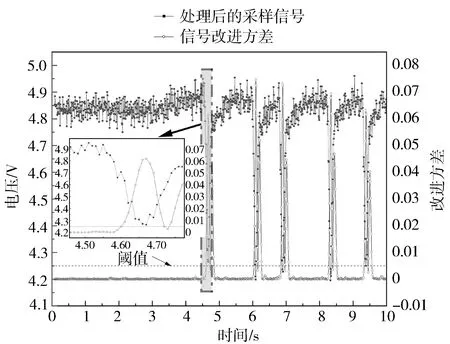
图11 JP60在100 000 r/min的压力信号及其检测计算结果
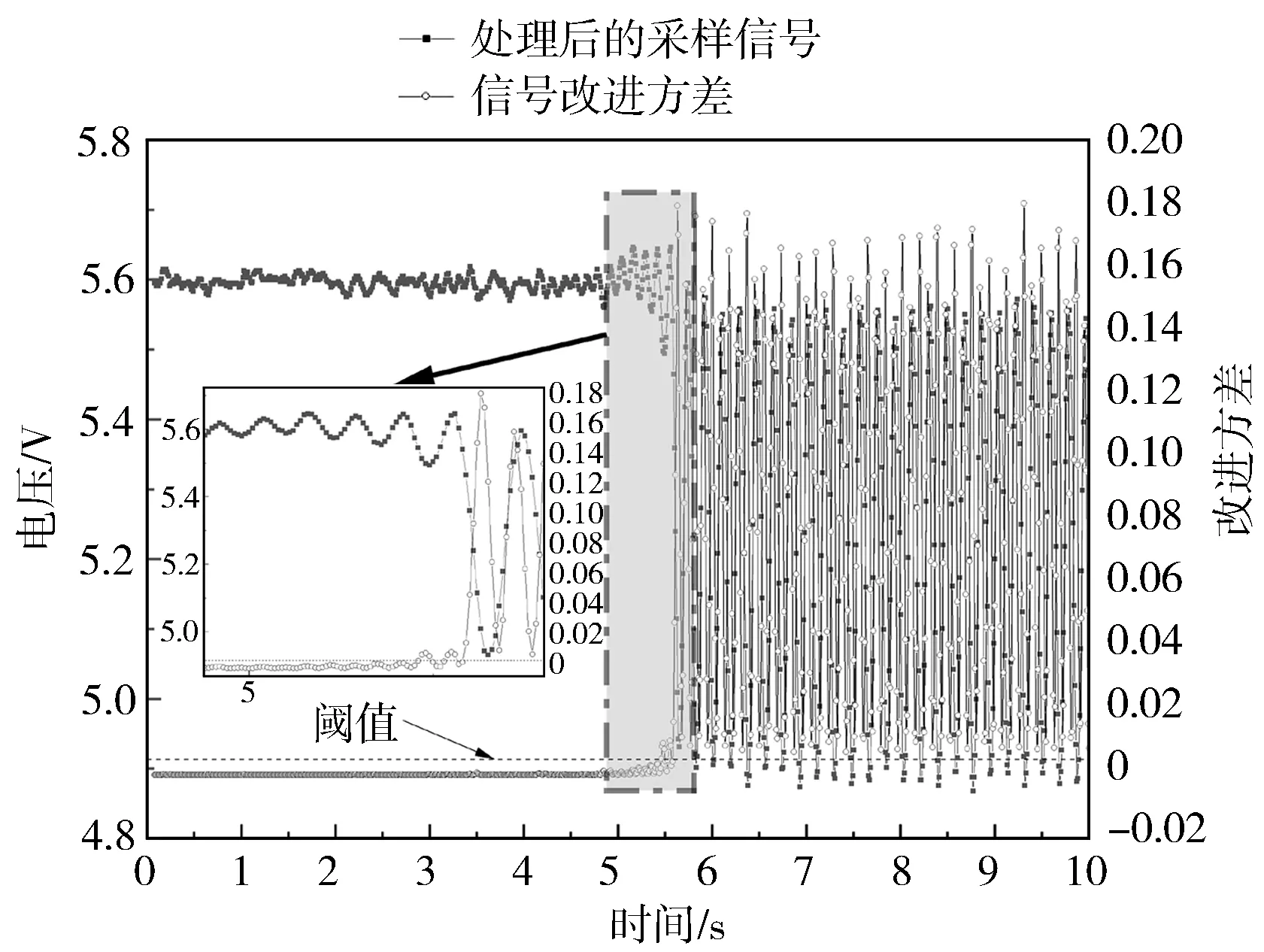
图12 JP90在60 000 r/min的压力信号及其检测计算结果
4 结论
a) 应用改进方差法检测喘振时计算结果与方差法相比其信噪比提高了20.5%;
b) 对于不同工况或类型的压气机喘振进行仿真试验,使用相同的阈值均在半个喘振周期内检测到喘振;
c) 采用的改进方差法根据所取的安全系数确定的阈值仅与气源波动和检测噪声相关,具有良好的通用性。
