基于优化高斯过程回归的谐波阻抗估计方法

夏焰坤 ，唐文张 ，林欣懿

（1.西华大学电气与电子信息学院，成都 610039；2.西南交通大学牵引动力国家重点实验室，成都 610031）

由于当前电力系统中存在电力电子设备的投切、高电压直流输电换流装置的使用和电力机车的启停等，导致电网中谐波源数量飞速增长，谐波污染不可避免，电网运行的稳定性亦会因此降低[1-2]。为有效抑制谐波污染，国际上提出了奖惩性方案，通过评判谐波发射水平并采用经济手段，对谐波负荷来源进行惩罚或对谐波受害者进行补偿[3]。

谐波责任分摊一直是电能质量分析的重点问题[4-5]。谐波功率方向法和阻抗参数法是应用于谐波责任划分中最广泛的两大类方法。其中，谐波功率方向法又包括谐波有功功率方向法[6]、谐波无功功率方向法[7-8]及谐波视在功率识别法[9]等。这些方法均是以功率方向为基础寻找谐波源的方法，因此谐波源的相位差对结果影响很大，特别是在大量新能源并网的今天，并不能保证此类方法始终适用。

阻抗参数法是当今国内外谐波水平研究中的热门方向，其重点是如何有效计算出系统侧谐波阻抗[10]。该方法由干预法和非干预法两个大类组成。其中，干预法主要采用添加支路的方式对电路强加谐波电流，通过响应的变化计算系统谐波阻抗。这种主动注入谐波电流的方式在谐波阻抗计算的实验搭建和结果准确性上具有显著优势，但是此类方法在大系统中对系统运行方式和稳定性的影响也不可忽视，值得研究人员持续关注和进一步研究。非干预法在近年来的研究过程中涌现出了一大批方法，例如波动量法[11]、回归法[12]、随机独立矢量协方差法[13]、盲源分离法[14]、支持向量机法[15]等。这些方法均在一定程度上解决了相应的实际问题，例如文献[16]提出了二元线性回归法，将观测值拆分为实部和虚部，通过线性回归获得系统谐波阻抗，原理简单，解决了谐波阻抗求解难的问题；文献[17]提出了改进的随机独立矢量协方差法，解决了观测数据中相位缺失或者相位不能直接测得的问题；文献[18]提出了支持向量机法，解决了观测值样本少、维数高、非线性及具有局部极小点等问题。背景谐波波动性较大、系统侧谐波与用户侧谐波具有关联性等问题仍是谐波阻抗估计中的难点，故很难评判某些方法的泛化性能，需更进一步研究。

为解决上述问题，本文提出一种优化高斯过程回归的谐波阻抗计算方法。高斯过程回归[19-20]已普遍应用于负荷预测、时间序列和计算机应用等领域，受到大量专家学者的青睐。贝叶斯优化算法[21]是一种全局优化算法，作为一种优秀的超参数调优方式，将其运用于高斯过程回归中寻找最优超参数。本文以公共连接点PCC（point of common coupling）处谐波电压和谐波电流为基础，通过贝叶斯优化高斯过程回归BO-GPR（Bayesian optimized Gaussian process regression）获得系统侧谐波阻抗，通过仿真分析与实例分析验证了该方法的有效性、准确性及泛化性能。

1 基本原理

1.1 谐波阻抗估计原理

戴维南等效电路和诺顿等效电路是电力系统谐波分析中两种常用的等效电路，如图1所示。其中，Us为系统侧等效谐波电压源；Zs为系统侧谐波阻抗；Is为系统侧等效谐波电流源；Ic为用户侧等效谐波电流源；Zc为用户侧谐波阻抗。

图1 等效电路Fig.1 Equivalent circuits

对谐波等效电路分析可得以下方程组：

式中，Upcc、Ipcc分别为PCC处的谐波电压和谐波电流。通过优化高斯过程回归获得Upcc、Ipcc与Zs的内在联系，即可估计系统侧谐波阻抗。

1.2 高斯过程回归

高斯过程回归在处理低维、小样本和非线性问题中具有显著优势，作为一个随机分布，其任意随机变量的有限子集均服从联合高斯分布。

式中：f()为映射函数；εi为服从高斯分布N～(0 ,σ2)的高斯白噪声。

在数据集T的有限集合中，一个联合高斯分布由[f(x1),f(x2),…,f(xi)]组成，其高斯过程模型可完全由均值函数与协方差函数决定，即

式中：GP()为高斯分布；X、X′为任意随机变量，X,X′∈Rk；m()为均值函数；k(X,X′)为协方差函数，即核函数；E()为期望。高斯过程回归常见的核函数包括平方指数核、Matern32核、指数核、有理二次核等。本文选用平方指数核作为核函数，具体形式为

式中：σf为标准偏差；σl为特征长度标尺。

当式（3）中m(X)=0时，观测值Y的先验分布可表示为

式中：K(X,X)为n维对称阵；为噪声协方差矩阵，其中σn为方差，In为单位阵；kij为向量Xi和Xj的相似程度，kij越大表示两个变量越相似。

给定测试样本X*，则其预测值Y*与训练样本的观测值Y组成的联合先验分布为

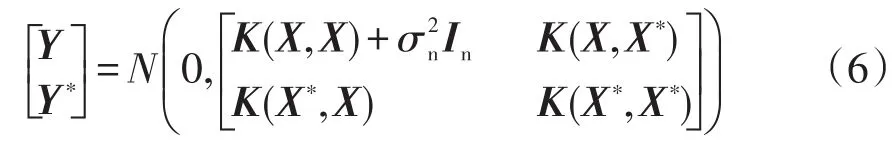
式中：N(0,·)为高斯分布；X为训练样本输入；X*为测试样本输入；K(X,X)为训练样本输入的协方差矩阵；K(X,X*)为训练样本与测试样本间的协方差矩阵；K(X*,X)=K(X,X*)T；K(X*,X*)为测试样本输入的协方差矩阵。

通过边缘化上述联合分布，可得到预测值Y*的后验分布为

式中：*为预测均值；σ2(Y*)为预测方差。

一般情况下，高斯过程回归中的超参数集合θ=[σf,σl,σn]可采用极大似然估计求解最优值，其对数似然函数L(θ)为

式中，n为矩阵维度。通过共轭梯度法或牛顿法等求解极大似然函数即可获得超参数集合。

1.3 贝叶斯优化

最优化超参数本质上就是求取一个函数的极值，若函数形式未知或函数为非凸函数，则梯度优化等方法无法解决。贝叶斯优化恰能解决这类问题，贝叶斯优化算法是一种基于模型的序贯优化方法，其优势在于只需要不断采样来推测函数的极值，经过一次评估之后再进行下一次评估，仅需少数次目标函数评估即可获得最佳参数，是一种有效的全局优化方法。故贝叶斯优化在实际问题中可能比其他优化方法具有更好的效果。

贝叶斯优化可在一定范围内求解目标函数的最优值，即

式中：x*为最优值；A为变量x的搜索空间；f(x)为由概率代理模型拟合的目标函数。

贝叶斯优化中有两个关键部分：①使用概率代理模型代替复杂的目标函数；②通过代理模型构造采集函数。

1.3.1 概率代理模型

贝叶斯优化中概率代理模型的参数更新依据贝叶斯定理，可表示为

式中：p(f|D1:i)为f的后验概率分布；p(D1:i|f)为y的似然分布；p(f)为f的先验概率分布；p(D1:i)为边缘似然分布；D1:i为观测样本集，D1:i={(x1,y1),(x2,y2),…,(xi,yi)}。

概率代理模型可分为参数模型和非参数模型。常见的参数模型有线性模型、广义线性模型、贝塔-伯努利模型。相比于参数固定的参数模型，非参数模型更具灵活性和可扩展性，在贝叶斯优化中不易出现“过拟合”，非参数模型主要包括高斯过程、随机森林、深度神经网络等。

1.3.2 采集函数

采集函数是一种根据后验概率分布主动选择下一个样本点进行优化的策略，包括基于提升策略的概率改善 PI（probability of improvement）、期望改善EI（expected improvement）及基于置信边界策略的置信上限UCB（upper confidence bound）等。

本文中采用基于EI策略的采集函数，可表示为

式中：V*为最优值；μi(x)为均值；ϕ(M)为高斯分布累计密度函数；M=[V*-μi(x)]/σi(x)；σi(x)为标准差；α(x;D1:i)为目标函数。

1.4 BO-GPR计算谐波阻抗

将BO-GPR用于谐波阻抗计算，计算流程如图2所示。具体步骤如下。

图2 BO-GPR流程Fig.2 Flow chart of BO-GPR

步骤1通过PCC处测量数据获得一定数量的样本，选择部分样本为训练样本，输入为谐波电压Upcc与谐波电流Ipcc组成的二维向量，输出为谐波阻抗Zs。再选择一定数量的样本作为测试样本，组成结构与训练样本一致。

步骤2根据训练样本进行高斯过程回归获得模型。

步骤3构造类似式（12）的代理模型及式（13）和式（14）的采集函数，使用贝叶斯优化获得噪声标准差σn的最优值。将σn的最优值代入高斯过程回归模型中的式（8）和式（9）得到最终的回归模型。

步骤4对比BO-GPR与其他方法的计算结果，评价本文方法的鲁棒性、准确性及泛化性能。

2 仿真分析

仿真分析中，分别采用4种方法对谐波模型进行阻抗估计。其中，方法1为二元线性回归法；方法2为支持向量机法；方法3为独立矢量协方差法；方法4为本文方法（BO-GPR法）。

2.1 背景谐波为非高斯分布的仿真

根据图1中等效电路在Matlab软件中建立背景谐波为非高斯分布的谐波分析模型（仿真1），系统频率为50 Hz，具体参数设置如下。

（1）系统侧谐波电压源为 100 V∠53.13°。

（2）用户侧谐波电流源为Ic=(4.73+j4.74)A，并在实部添加0.42 A的扰动电流，虚部添加0.41 A的扰动电流。

（3）谐波阻抗中系统侧谐波阻抗为Zs=(6+j25)Ω，并在实部添加0.1 Ω的扰动阻抗，虚部添加0.3 Ω的扰动阻抗；用户侧谐波阻抗为Zc=(6+j25)Ω，并在实部添加0.1 Ω的扰动阻抗，虚部添加0.3 Ω的扰动阻抗。

表1 阻抗均值Tab.1 Mean impedance

由表1结果可知，除方法3的计算阻抗误差较大外，其余3种方法均获得了很好的计算结果，但本文方法（方法4）相对而言最精确，其计算阻抗与真实阻抗完全一致，故当背景谐波为非高斯分布时，本文方法在谐波阻抗计算中具有高准确性。

2.2 背景谐波为高斯分布的仿真

为探究本文方法在不同背景谐波下的效果，根据图1中诺顿等效电路建立背景谐波为高斯分布的仿真模型，系统频率为50 Hz，具体参数设置如下。

（1）系统侧谐波阻抗Zs服从高斯分布Zs～N(2+j6,0.1+j0.3)，Ω。

（2）用户侧谐波阻抗Zc服从高斯分布Zc～N(20+j160,0.5+j5)，Ω。

（3）用户侧谐波电流源Ic服从高斯分布Ic～N(6+j8,0.3+j0.4)，A。

（4）系统侧谐波电流源Is为Ic的k倍，其中k从0.2～1.0每隔0.2取1个值。

表2 阻抗均值实部Tab.2 Real part of mean impedance

表3 阻抗均值虚部Tab.3 Imaginary part of mean impedance

对表2和表3的结果纵向比较，方法1的误差随k的增大而增大，甚至超过了100%，说明该方法在背景谐波非线性程度较高时效果较差；方法2的误差随k的变化也有一定的波动，误差波动范围在7%以内，相对较稳定；方法3的误差随k的变化趋势类似于方法1，其误差相对于方法1更小，但仍然具有较大的误差，独立矢量协方差法只能在Is与Ipcc具有弱相关性或者近似独立时实现，而该仿真下这项前提条件并不成立，故出现较大误差；本文方法（方法4）是4种方法中误差最小的，且方法4的误差几乎不随k值的变化而变化，具有显著的稳定性。

再结合表1中的数据进行对比可知，方法1在不同的背景谐波下效果差异明显；方法2在背景谐波特性变化时效果较好，也具备较高的稳定性；方法3在两种背景谐波下均出现较大的误差，计算结果在源数据相关性较大时失去参考意义；本文方法（方法4）在两种背景谐波下均具有极小的误差，很大程度地抑制了背景谐波变化以及谐波电流源呈一定相关性带来的误差，体现出较好的泛化性能。

3 实例分析

实例分析数据来自某变电所带牵引负荷的110 kV母线。使用电能分析仪测量PCC处的电压和谐波电流，进行快速傅里叶变换得到谐波电压与谐波电流，本文以3次谐波为例。在PCC处每隔3 s测量1次，在10 h内共得到12 000个样本，分析基波电压及电流，去除样本中的空载点、轻载点及离群点，选择800个负载样本作为研究对象，得到PCC处带负载3次谐波电压和谐波电流如图3所示。

图3 带负载时的3次谐波电压与电流Fig.3 Third harmonic voltage and harmonic current with load

实例分析中参考阻抗为（26.45+j42.77）Ω，值得注意的是，此前的研究中常采用二维图像展示结果，考虑到输入数据是二维矢量，输出为一维矢量，使用三维图像更能凸显各方法之间的差异。在方法4的计算过程中，将筛选后的谐波电压与谐波电流进行优化高斯过程回归，并对结果进行插值，得到3次谐波阻抗如图4所示。使用均值、平均误差、均值最大偏差、标准差、均方根误差及运算时间等指标评价其结果，本文方法得到的指标参数如表4所示。

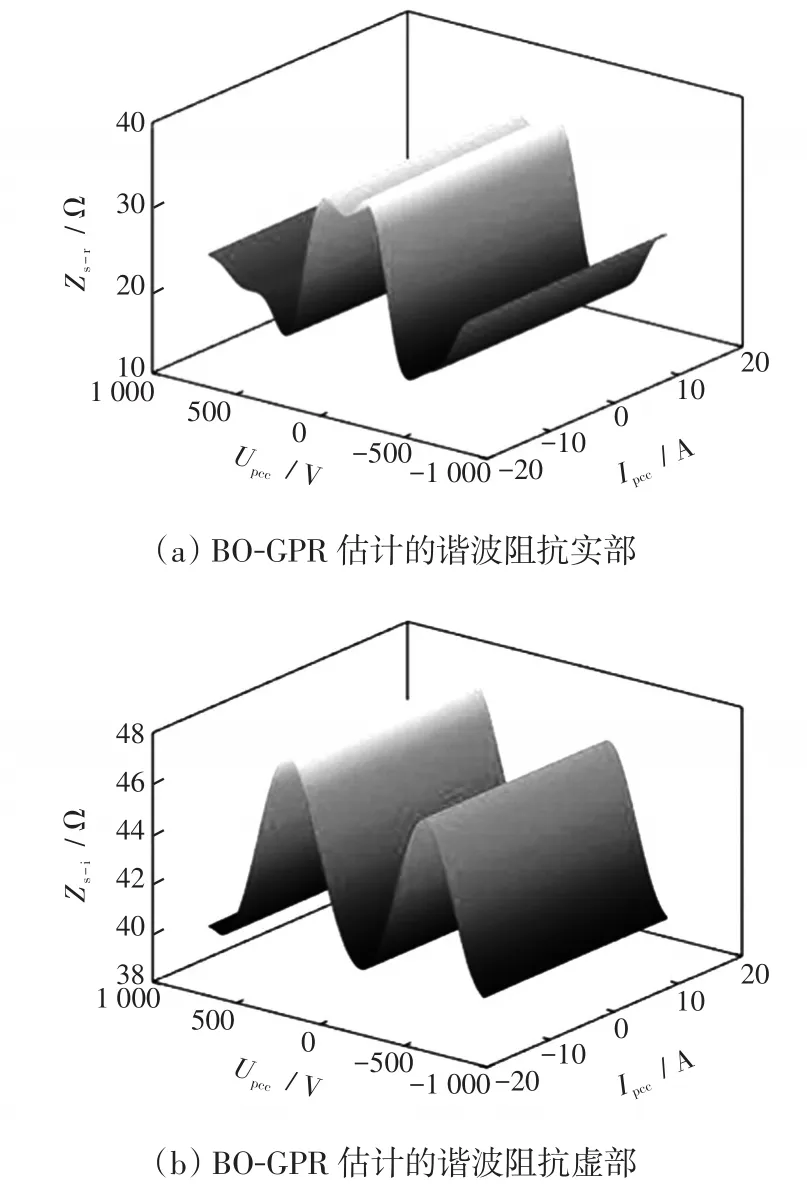
图4 通过BO-GPR得到的谐波阻抗Fig.4 Harmonic impedance estimated by BO-GPR

前3种方法实部和虚部的估计阻抗如图5～图7所示。前3种方法各项指标参数见表5～表7。

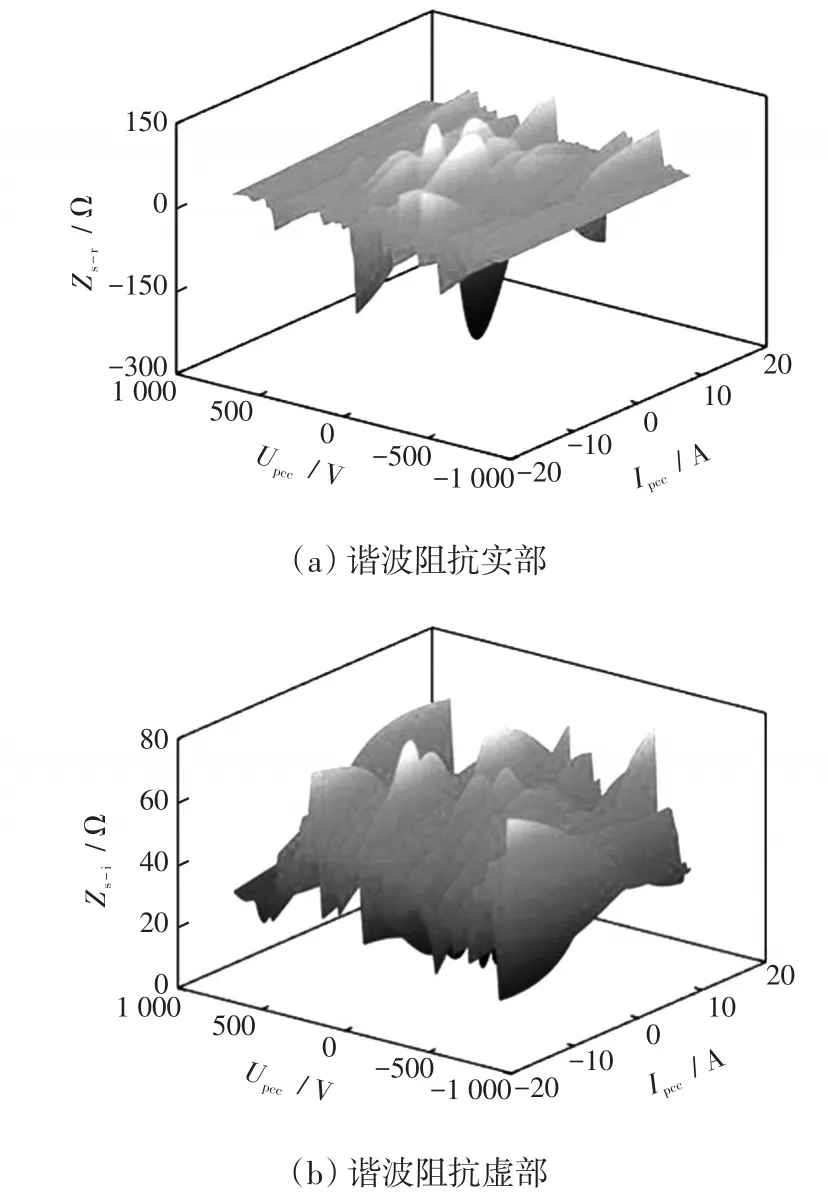
图5 通过二元线性回归得到的谐波阻抗Fig.5 Harmonic impedance estimated by bivariate linear regression

图6 通过SVM得到的谐波阻抗Fig.6 Harmonic impedance estimated by SVM

图7 通过独立矢量协方差得到的谐波阻抗Fig.7 Harmonic impedance estimated by random vector covariance

表5 二元线性回归的评价指标Tab.5 Evaluation indicators for bivariate linear regression

表6 SVM的评价指标Tab.6 Evaluation indicators for SVM

表7 独立矢量协方差的评价指标Tab.7 Evaluation indicators for random vector covariance

对比图4～图7及表4～表7可知，方法1计算方式简单，运行时间短，虽然均值接近参考阻抗，但实测谐波数据不平稳且线性程度低，导致其他指标均不理想；方法2在运算中可能陷入局部最优，使得其结果出现偏差，并且显示出一定的波动性；方法3在4种方法中效果最差，在系统侧与用户侧谐波发射有一定联系的情况下，因不满足方法3的前提条件而出现不适用性；本文方法（方法4）各项指标均优于其他3种方法，具有一定有效性和实用性，从图4可以看出，BO-GPR的结果可视化后得到的谐波阻抗实部、虚部在谐波电压与谐波电流的正负半轴上具有一定的对称性，谐波阻抗具有相对较小的波动性，唯一的不足是计算时间较长，不具实时性。

4 结语

本文将高斯过程回归与贝叶斯优化相结合并用于计算谐波阻抗中，提出了一种BO-GPR的谐波阻抗计算方法，旨在解决背景谐波波动较大、系统侧谐波与用户侧谐波有一定关联程度情况下的谐波阻抗计算问题。仿真分析验证了本文方法准确性和稳定性较好，实例分析验证本文方法具有一定的有效性和实用性。本文方法具有显著的优势和不足，其优势在于：①可以降低非线性背景谐波对结果的影响；②能够避免陷入局部最优；③实例分析中系统侧谐波与用户侧谐波或有一定关联程度，本文方法对PCC处谐波电压和电流的相关性没有要求；④在背景谐波特性不同的情况下可得到较好结果，具有较好的泛化性能。但是，本文方法计算用时相对较长，在系统稳定运行时可根据已生成模型计算阻抗，而若系统出现故障或拓扑结构发生改变，此法难以快速反应。如何在保证结果准确的情况下增强方法的时效性将是进一步研究的方向。