基于Attention机制优化CNN-seq2seq模型的非侵入式负荷监测

王琪凯，熊永康，陈 瑛，夏永洪，叶宗阳，余礼苏

（南昌大学信息工程学院，南昌 330031）

非侵入式负荷监测NILM（non-intrusive load monitoring）[1-3]又称非侵入式负荷分解。与传统负荷监测需要在每个设备上安装传感器，来获取用户用电信息的侵入式负荷监测ILM（intrusive load monitoring）不同，该技术只需要在用户入口处安装监测装置，采集功率、电压、电流等汇总的总负荷信息，就能分解得到所需单个设备的用电信息。NILM技术在成本及后期维护上，相比ILM更具优势[4-5]。在用户用电需求持续增长、智能电网[6]等技术快速发展的今天，NILM技术在兼顾用户隐私[7-8]的同时，可以推动电网侧和用户侧友好互动，鼓励用户积极参与到节能计划中[9-10]，对于实现“碳达峰、碳中和”目标具有重要意义。

NILM最早由Hart[11]于20世纪80年代提出，负荷特征一般可以分为暂态特征和稳态特征[2]。其中，基于暂态特征的算法以瞬时功率变化、启动电流波形、电压噪声等特征信息来判断负荷状态是否发生改变。文献[12]提出一种改进的基于时频分析的NILM方法，结合多分辨率S变换的瞬态特征提取方案和改进的0-1多维背包算法来识别设备运行情况。文献[13]将设备状态转换过程中的暂态功率波形及状态改变前后的功率变量作为负荷特征，采用动态时间规整DTW（dynamic time warping）算法将其与历史暂态事件波形匹配并进行动态聚类，使用关联规则分析找出属于同一设备的暂态事件集。即便如此，基于暂态特征识别的算法存在需要获取高频采样数据、对设备硬件要求高的特点。相比较而言，基于稳态特征识别的算法所需要的低频采样数据，智能电表一般就能提供支持[1]。根据辨识的负荷类型、用户对识别精度的要求等情况，居民用户可以考虑选择低频负荷特征[1]。基于稳态特征的算法一般以有功、无功信号作为输入来分解得到单个设备运行情况。文献[14]提出一种情境自适应和贝叶斯优化的双向长短期记忆BiLSTM（bidirectional long short-term memory）网络模型，使用3种开源数据集，从季节、地理、设备型号等角度证明模型具有良好的适用性。文献[15]提出一种数据扩充技术，提高了训练数据集的质量，使用深度卷积神经网络CNN（convolutional neural networks）模型进行分解，同时提出一种后处理技术，可以有效剔除一些不合理的结果，对Ⅱ类负荷（多状态设备）具有良好的分解性能。

上述基于稳态特征的算法，其核心结构都是基于深度学习网络框架建立的。文献[16]提出了一种CNN-BiLSTM算法应用于NILM领域，是目前公认的利用深度学习所达到的综合性能最优的模型[17]。为了进一步提高模型的分解性能，本文在文献[16]的基础上，对其所述算法进行以下改进。

（1）序列到序列seq2seq（sequence-to-sequence）模型的独特优势是能将1个序列问题转换成另一个序列问题，seq2seq的基本单元仍是BiLSTM和长短期记忆LSTM（long short-term memory）。使用seq2seq结构替代BiLSTM结构，更适合NILM的分解模式，且能有效地挖掘时序特征信息，同时在模型搭建上也更加灵活。

（2）引入注意力机制优化整体模型，使得模型能够更加关注重要部分的特征。

1 模型流程

本文所用NILM流程如图1所示，具体步骤如下。

图1 模型流程Fig.1 Flow chart of the proposed model

步骤1对原始数据进行归一化后，进行数据切片。该步骤有利于不割裂地处理每个时刻的信息，因为设备运行是一个连续过程，当前时刻的设备状态一定程度上也与之前时刻的运行状态相关。将处理后的序列数据作为输入传入训练模型中。

步骤2对历史的设备数据进行聚类操作，生成负荷聚类-编码表。这是因为设备实际运行过程中，由于噪声等原因，其运行过程中会存在一定的波动，因此本文使用这些聚类结果代替设备不同状态（模式）下的功率，从而降低分解难度和提高分解精度。

步骤3将聚类结果转换成状态编码，作为输出传入到训练模型中，简化了模型的输出结构，有助于输出和步骤1中的输入形成一一映射关系。

步骤4将处理好的数据分成训练集和测试集，训练集用于训练模型，测试集用于检验模型分解性能。

步骤5所搭建的模型根据步骤1和步骤3输入的数据，不断训练、迭代，找出数据之间的映射关系，调整模型内部参数。

步骤6将当前时刻总功率序列数据（测试集）输入训练好的模型中，模型就能自主地给出当前时刻每个设备对应的状态概率分布矩阵，并根据所得设备状态结果与负荷聚类-编码表进行比对，得到具体的有功功率。

2 数据预处理

2.1 负荷特性分析

电力负荷按照行业性质主要划分为商业负荷、工业负荷和居民负荷等[2]。这些负荷之间的特征存在明显差异，例如工业负荷一般功率较大，受订单、季节等因素影响；商业负荷以照明、电脑用电等为主，受工作日、节假日等时间因素影响；居民负荷种类众多且功率范围跨度广，受用户习惯影响。因此，对于不同行业、工程项目的负荷分解难度、具体分解方法和细节也有所不同。家电设备可以分为开/关二状态型、有限多状态型、连续变状态型和永久运行型4类[2]。居民负荷多为前2种，其工作示意如图2所示。

图2 开/关二状态及有限多状态负荷Fig.2 On/off two-state and finite state load

2.2 K-means++聚类

本文选择6种家电设备作为分解负荷，分别为干衣机、热泵、冰箱、洗碗机、电视和地下室灯（数据描述详见第5.1节）。使用K-means++算法对上述设备进行聚类操作，具体步骤如下。

步骤1在当前设备N个样本点中，随机抽取1个点作为第1个聚类中心c1。

步骤2计算每个样本点与当前已确定聚类中心之间的最短距离D(xi)，可表示为

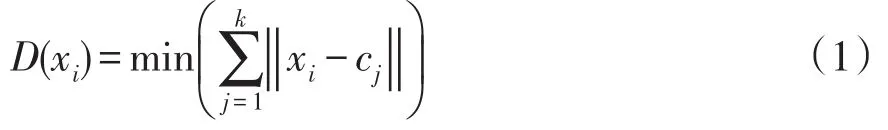
式中：xi为第i个样本点；cj为第j个聚类中心；k为当前已确定的聚类中心个数；‖‖为欧式距离；min()为最小值函数。

步骤3计算每个样本点成为下一个聚类中心的概率P(xi)，可表示为

步骤4重复步骤2和步骤3，直至选出的初始聚类中心个数达到该设备的状态个数。

步骤5计算每个样本点与所选聚类中心的距离，将其划分给距离最近的聚类中心，并标记所属簇的标签。

步骤6计算每个簇中所有样本点坐标的平均值，以此作为该簇新的聚类中心。

步骤7重复步骤5和步骤6，直至算法收敛。

K-means++聚类所得结果如表1所示，其中状态0～3为本文根据聚类结果定义的设备工作状态，并匹配对应的独热码。

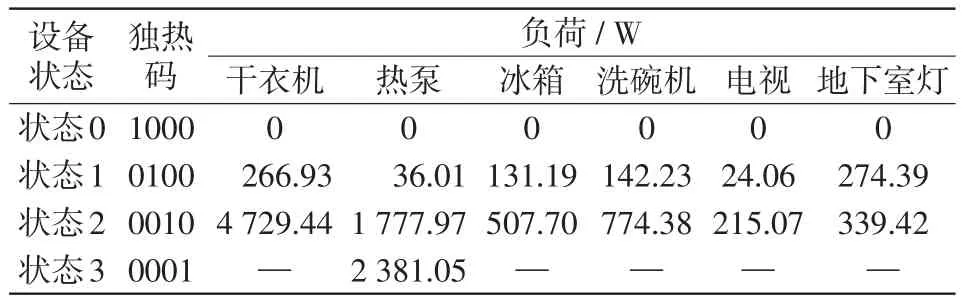
表1 负荷聚类-编码表Tab.1 Table of load clustering-coding

2.3 数据处理及状态编码

神经网络模型激活函数的有效工作范围一般为[-1，1]，因此需要对总有功功率数据进行归一化处理，归一化公式为

式中：x′为归一化后的结果；x为真实值；xmax、xmin分别为有功功率的最大值和最小值。

当前时刻各设备的状态不仅与当前时刻的总负荷信息相关，还和之前时刻有关，因此需要将数据切片化处理，使其成为时间序列向量，即

根据表1所得聚类结果，将原始数据中每个设备所记录的实际有功功率转换为对应设备状态，然后通过独热码处理以匹配本文模型。因此，NILM技术中每个设备状态独热码和时间序列数据的映射关系可表示为

3 基于注意力机制优化的CNN

CNN在自然语言处理、计算机视觉等领域被广泛应用，主要由卷积层、池化层和全连接层构成。其中，一维卷积神经网络在时间序列数据的特征信息提取上具有良好表现。一维卷积的计算公式为

本文引入SENet（squeeze-and-excitationnetwork）模块[18]，这是一种优化CNN特征通道的注意力机制。该结构通过学习全局信息，能够选择性地提高重要特征通道的权重，同时抑制非显著特征，从而达到提高CNN性能的目的，其结构如图3所示。本文将式（4）所得到的总有功功率时间序列向量，通过2层卷积层得到B×C×W的特征矩阵U，其中B为模型的批处理个数，C为特征通道数，W为特征长度。

SENet模块的优化过程分为压缩和激发两步，如图3所示。压缩操作使用全局平均池化将负荷的全局信息压缩，计算公式为

图3 SENet模块Fig.3 SENet block

式中：zc为通道c的压缩值；ui为通道c上第i个特征值。

激发操作利用两层全连接层FC（fully connected layers）捕获通道之间的依赖关系。第1层全连接层将式（7）所得压缩信息转换成维度；然后使用第2层全连接层将其再次变为B×C×1。这种处理方式使得通道之间的压缩信息能够进行充分非线性交互，有利于捕捉依赖关系，得到通道权重系数，其计算公式为

式中：s为通道权重向量；w1、w2分别为第1层、第2层全连接层的参数；z为式（7）所得所有通道信息压缩值；δ为第1层全连接层的ReLU激活函数；σ为第2层全连接层的Sigmoid激活函数。

最后，通过式（9）将特征矩阵U和所得通道权重向量s相乘，得到优化后的特征矩阵X′为

本文所用CNN分为2层：第1层卷积层的卷积核个数为16，尺寸为3，激活函数选择ReLU函数；第2层卷积层的卷积核个数为32，尺寸为3，激活函数选择ReLU。

4 基于注意力机制优化的seq2seq网络

4.1 编码结构

seq2seq模型分为编码和解码2个部分，常被用于处理序列到序列的任务。本文所用seq2seq网络的核心思想为通过编码-解码结构对CNN进行处理，得到的特征序列转换为状态概率分布序列。基于注意力机制优化的seq2seq结构如图4所示，其中seq2seq的基本单元为LSTM网络。

图4 基于注意力机制优化的seq2seq结构Fig.4 Structure of seq2seq optimized by Attention mechanism

编码结构使用BiLSTM网络替换单向LSTM，因为BiLSTM网络能够更加充分地利用输入的所有序列信息[19]。BiLSTM网络当前时刻的隐藏层状态的计算公式为

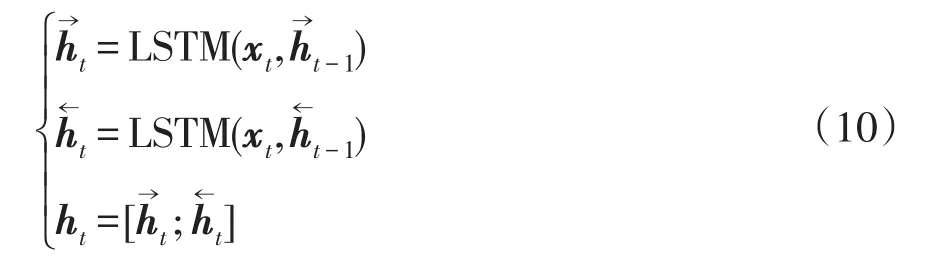
LSTM单元包含遗忘门、输入门和输出门。输入门控制当前时刻的输入值，遗忘门对上一时刻记忆单元状态进行选择性地遗忘，输出门汇总两者信息决定输出值，从而能够实现对时间序列数据的特征提取。LSTM单元可表示为

式中：it、ft、、ot、ct和分别为输入门、遗忘门、候选记忆单元状态、输出门、记忆单元状态和当前时刻隐层状态；Wix、Wfx、Wcx和Wox为相应门与当前时刻输入xt的权重矩阵；Wih、Wfh、Wch和Woh为相应门与上一时刻隐层状态的权重矩阵；bi、bf、bc、bo为相应门中的偏置向量；σ为激活函数Sigmoid；tanh()为双曲正切函数；⊙表示向量中元素按位相乘。

4.2 注意力机制

如图4所示，本文在seq2seq模型中引入注意力机制[20]。解码结构在产生新状态前，先读取编码中所有时序的隐藏层输出向量H=[h1,h2,…,hm]，其中m为隐藏层状态个数，并使用注意力机制对H分配不同比重，使得网络能够有针对性地关注有效特征信息。解码结构产生新状态的公式为

式中：st为解码结构中当前时刻的隐藏层状态；st-1为上一时刻隐藏层状态；Ct为当前时刻时序向量；yt-1为上一时刻设备的状态概率密度分布向量。

动态可变的时序向量Ct能够储存当前时刻模型输入的完整有效信息，其计算过程如下。

步骤1通过2个全连接层计算注意力机制得分，其计算公式为

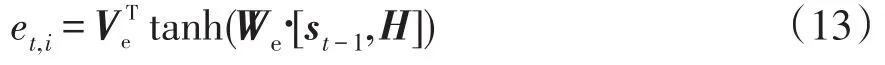
式中：Ve、We为相关权值矩阵；et,i为当前时刻第i个隐层状态的注意力得分；H为编码中所有时刻隐藏层的输出向量；[st-1,H]表示矩阵st-1与H拼接。

步骤2对式（13）得到的et,i使用softmax函数计算各隐层状态的权重，即

式中：m为编码中所输出的隐藏层状态个数；αt,i为当前时刻第i个隐层状态所对应的权重；et,k为根据式（13）求得第k个et,i的值。

步骤3根据式（14）求得各隐层状态权重αt,i及其对应隐层状态hi，加权相加得到动态时序向量Ct，即

式中，hi为由式（10）求得的第i个ht。

4.3 解码结构

解码结构用来得到最终的分解结果，该部分将CNN所得总有功功率时序特征序列转换为设备状态序列。与编码部分不同，解码必须使用单向LSTM网络，因为解码是设备状态生成器，需要按顺序生成每个设备的状态编码。从图4可以看出，解码结构中LSTM层的初始状态s0源自编码中BiLSTM层最后1个隐层状态hm。值得注意的是，隐层状态是由正向、反向的2个隐层状态拼接而成，其维度与s0所需维度不匹配，因此需要经过1个全连接层将hm压缩后传入解码。

图4中解码接收上一时刻（上一个设备）隐层状态st-1、当前时刻时序向量Ct和上一时刻设备的概率输出yt-1（第1个时刻需要设置起始符），通过式（12）可以得到当前时刻的隐层状态st。将st、Ct和yt-1拼接后，通过全连接层得到当前设备的概率密度分布yt。st、Ct和yt-1拼接可表示为

式中，f1()为全连接层的内部处理方式。

每个设备的状态个数不同，因此不同设备进行概率分布yt预测时，需要使用如图4所示不同的全连接层处理，其中全连接层神经元个数为设备状态类别数目。设所有设备中最大状态个数为kmax，当使用上一个设备概率分布向量yt-1来预测当前隐层状态st时，若yt-1的维度小于kmax，则需要将其用零向量扩展至kmax维。

对于本文模型得到的yt，通过式（17）选取概率最大的状态作为该设备当前时刻的分解状态，最后将其转换为如表1所对应的功率值。具体计算公式为

式中，argmax()为最大值索引函数。

本文所用BiLSTM层的隐藏层神经元个数为32，LSTM层的隐藏层神经元个数为32。

4.4 模型训练

本文模型通过聚类和编码操作，将分解问题转换为求解各个设备状态的多分类问题，因此使用CrossEntropyLoss交叉熵函数作为模型训练的损失函数，即

式中：lossi为第i个样本的损失；xt,i为第i个样本各个状态的概率分布矩阵；n͂为设备状态个数；classi为第i个样本的所属真实状态类别；N为样本个数；xt,i[classi]为矩阵xt,i中第classi维代表的数值；xt,i[j]为矩阵xt,i中第j维代表的数值。

为避免网络出现过拟合现象，本文在模型训练过程中，对于解码部分，50%概率将上一个设备真实状态编码作为输入，50%概率以模型预测值yt-1作为输入。最后，本文使用Adam优化器，根据梯度更新网络参数，学习率为0.001，迭代次数为100次。

5 算例分析

5.1 数据集选取

本文采用AMPds2开源数据集[21]，该数据集记录了加拿大某居民2 a内的各种设备监测数据，采样时间间隔为1 min。本文使用该数据集中的干衣机、热泵、冰箱、洗碗机、电视和地下室灯6种设备（2 a间有功功率）作为分解负荷，同时选取105组数据作为测试集用来验证本文模型效果。

5.2 硬件环境及软件平台

本文硬件环境为Intel（R）Core（TM）i5-9300H CPU@2.40 GHz、8 G DDR4内存、GeForce GTX 1650的笔记本；Intel（R）Xeon（R）Gold 5218 CPU@2.30 GHz 2.29 GHz、256 G DDR4内存、GeForce RTX 2080 Ti的服务器。

软件平台为Windows10操作系统，Python 3.6.8（64位）及PyTorch 1.9.0深度学习框架，在训练网络时使用GPU进行硬件加速。

5.3 评价指标

本文所用评价指标分为评价设备状态分解准确率和评价设备功率分解准确性两部分。使用状态识别准确率AS评价模型对于单个设备整体的分解效果。由于家电设备的关闭状态时间远大于开启状态时间，使用该评判标准并不能很好地体现模型的性能，因此定义设备运行（非关闭）状态识别准确率ARS。AS和ARS可分别表示为

对全部状态和运行状态进行归一化，其RMSE可分别表示为

式中：NS为样本点总数；n′为正确识别设备状态的样本点个数；TS,i为第i个正确识别设备状态的样本点；NRS为运行状态的样本点总数；m′为正确识别设备运行状态的样本点个数；TRS,i为第i个正确识别设备运行状态的样本点；Pi为第i个真实功率值；P̂i为第i个分解功率值；RMSES、RMSERS分别为全部状态的归一化均方根误差和运行状态的归一化均方根误差，RMSES及RMSERS越小表示设备分解准确度越高。

5.4 结果分析

为验证本文所提算法，将其与文献[16]所述CNN-BiLSTM算法（简称CB算法）及CNN-seq2seq算法（无注意力机制优化，简称CS算法）进行比较。部分分解曲线如图5和图6所示。由于同一时刻并不是所有家电设备都处于运行状态，为了更好地展示分解效果，图5和图6中所展示设备并非处于同一时刻。图5为不同时刻有多个设备共同叠加运行。图6为单个设备的分解结果。相比较而言，本文算法的分解效果更好。

图5 负荷叠加曲线Fig.5 Curves of load superposition

图6 各设备分解结果Fig.6 Disaggregation results of each equipment

设备状态识别准确率、功率分解准确性的结果如表2和表3所示。结合表1中各设备的聚类结果可以看出，设备单状态、组合状态之间具有相似性，例如冰箱状态1和洗碗机状态1功率相近，冰箱状态1、洗碗机状态1的组合状态与地下室灯状态1相近等。此外，由于设备运行过程中功率会产生波动等因素（见图6（e）中电视功率波动尤为明显），也增大了负荷分解的难度。

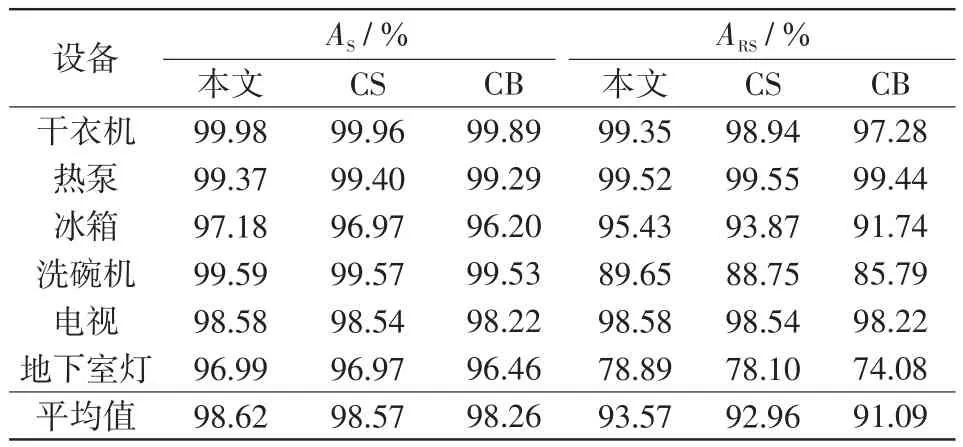
表2 不同模型的状态识别准确率Tab.2 State recognition accuracy of different models

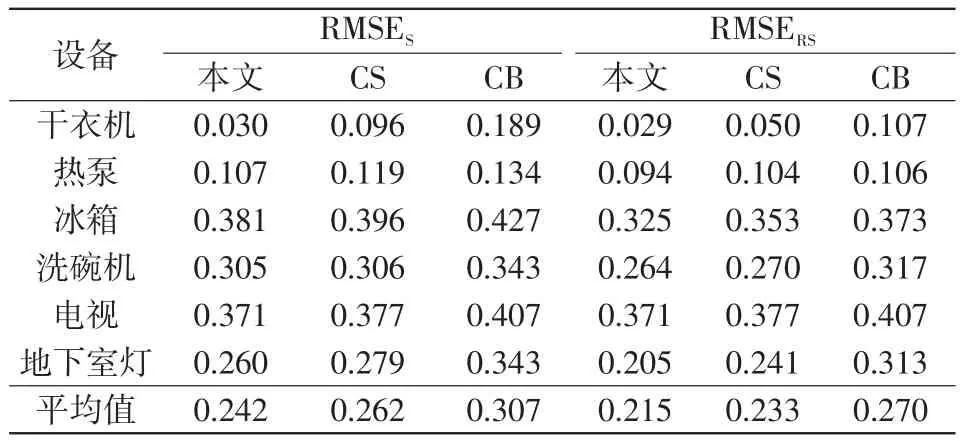
表3 不同模型的功率分解准确性（均方根误差）Tab.3 Power decomposition accuracy of different models（RMSE）

由表2和表3可知，使用seq2seq结构替代BiLSTM提高了模型分解精度，CS模型的状态识别准确率、均方根误差结果都优于CB模型；同时，本文模型的整体结果优于CS模型，表明在模型中引入注意力机制能够使得模型更加有效地关注重要部分的信息，进一步提高了模型精度。

总体上，本文所用模型的识别准确率AS和ARS都高于CB模型，其中冰箱、洗碗机和地下室灯的识别准确率提升较大。而在均方根误差方面，本文模型的平均RMSES比对照模型降低了21.17%，平均RMSERS比对照模型降低了20.37%，分解精度有显著提升。从算例分析可以看出，本文对CB算法的两处优化都是有效的，并取得良好的分解效果。

6 结语

本文提出了一种基于注意力机制优化的CNN-seq2seq模型用于NILM。将总有功功率数据构建成时间序列向量作为模型输入，通过K-means++聚类将功率数据转换成状态编码作为模型输出，简化了模型结构。同时注意力机制使模型能够更加关注重要特征信息。与在深度学习领域中具有较优性能的CNN-BiLSTM模型相比，本文模型的设备识别准确率较高，而且均方根误差也显著降低。

下一阶段将在指导居民用电行为、减少能耗等方面开展进一步研究。