基于窗口参数估计的距离扩展目标CFAR检测

郑志杰， 万显荣， 胡仕波， 谢德强， 童 云

(武汉大学电子信息学院， 湖北武汉 430072)

0 引 言

外辐射源雷达是一种自身不需要发射电磁波而是利用第三方辐射源进行目标探测的新体制雷达，具有节约频谱、设备体积小、易于组网、隐蔽性好等特点，是近年来新体制雷达领域的研究热点[1]，以数字电视信号为第三方辐射源的外辐射源雷达近年来得到了极大的发展，已广泛应用于各种军用和民用领域的无人机等“低慢小”目标和通用航空飞行器的探测。

数字电视外辐射源雷达所利用的第三方辐射源信号带宽较大，雷达距离分辨率较高。探测无人机和通航飞机这类尺寸小于距离分辨率的目标时将其作为点目标，采用合适的恒虚警检测算法如有序恒虚警(OS-CFAR)即可有效检测目标[2]，探测大尺寸目标如大型货轮等舰船目标时，目标尺寸远大于雷达距离分辨率，目标回波不再保持点目标回波的特征，而是在距离维上连续占据多个距离单元，这类目标被称作距离扩展目标[3]。此时如果仍然使用传统的点目标CFAR算法，会因无法充分利用全部目标回波能量而导致检测性能下降，进而影响雷达的探测性能，因此需要研究距离扩展目标检测方法。

距离扩展目标检测问题最早出现在高分辨率主动雷达和声呐系统中。文献[4]提出了高斯背景下的距离扩展目标二进制积累CFAR算法，在与目标长度相适应的距离维滑窗内进行双门限检测，即对第一门限检测结果进行二进制积累，将积累结果实施第二门限检测从而判定是否为距离扩展目标，研究表明该算法相较传统的点目标CFAR算法在检测性能上有较大提升。文献[5]则提出了模糊CFAR算法，在第一门限检测中用模糊CFAR检测器代替传统的二进制积累CFAR检测器，进一步充分利用待检单元的信息，首先将距离维滑窗内的待检单元值转换到虚警空间的模糊隶属函数值，然后采用模糊逻辑的积累准则对这些模糊隶属函数值进行积累得到检测统计量，最后与门限比较判决是否为距离扩展目标，常用的模糊积累准则有模糊代数和和模糊代数积，文献[6]又提出了模糊算数和积累准则。上述文献针对Swerling 0型非起伏目标和Swerling Ⅱ型起伏目标作了性能仿真分析，结果表明了模糊CFAR算法比二进制积累CFAR对以上起伏模型目标具有更好的检测性能。以上算法均需要预先知道目标所占据的距离元的个数，利用等宽度的滑窗进行窗口内目标检测，文献[7]提出了一种基于能量积累的距离扩展窗口估计方法，该方法计算速度快，但易受强距离旁瓣的干扰。

本文针对大尺寸目标在距离多普勒(RD)谱上发生距离扩展所造成的检测问题展开研究，首先建立了外辐射源雷达距离扩展目标的回波模型，且提出了基于最大广义信噪比的距离扩展窗口参数估计算法，采取约束条件下的二维网格搜索法求解，可同时得到窗口起始位置和宽度的估计值，避免了暴力法滑窗CFAR检测的高时间复杂度。在得到距离扩展窗口位置和宽度后，为进一步判断窗口内是否为距离扩展目标，研究了传统的二进制积累CFAR检测算法和模糊CFAR检测算法。最后开展了数字电视外辐射源雷达海面舰船目标探测实验进行实测数据处理。

1 外辐射源雷达距离扩展目标回波模型

外辐射源雷达目标探测原理如图1所示，发射站和接收站分置，分别为Tx、Rx，在不考虑杂波和噪声的情况下，参考通道接收到发射信号为r(t)，回波信号为s(t)，在目标O为点目标情况下，目标到发射站距离为RT，目标到接收站距离为RR，发射站到接收站的距离为基线距离L。

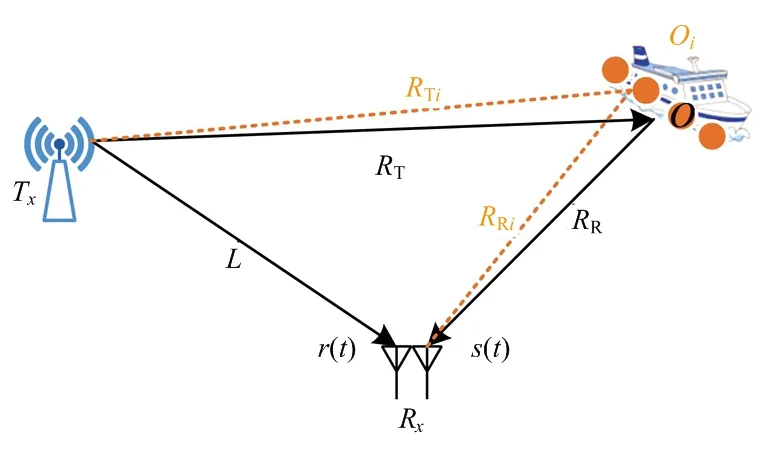
图1 外辐射源雷达目标探测示意图

当目标O尺寸远大于雷达距离分辨率时，其为距离扩展目标，目标回波为目标冲激响应与发射信号的卷积。距离扩展目标的冲击响应表示为

(1)

式中，S为距离扩展目标O在外辐射源雷达探测时目标散射中心的个数，ai为第i(i=1,…,S)个散射中心的幅度，τi为第i个散射中心的双基延时。设第i个散射中心到发射站距离为RTi，到接收站距离为RRi，则有

τi=(RTi+RRi-L)/c

(2)

那么距离扩展目标回波表达式为

sextended(t)=r(t)*hO(t)=

(3)

将目标回波sextended(t)与参考信号r(t)进行匹配滤波即可得到RD谱[8]，距离扩展目标在RD谱距离维上连续占据S个距离单元，然后在RD谱上进行目标检测，此时点目标CFAR检测算法将不再适用，将考虑利用距离扩展目标CFAR检测算法进行处理。

2 距离扩展窗口参数估计

距离扩展目标所占据的连续距离单元称为距离扩展窗口，其有两个参数：起始位置、窗口宽度。窗口宽度与目标的径向长度相适应，且影响距离扩展目标检测算法的性能，而且窗口的起始位置确定之后可以避免对整个距离维进行暴力法滑窗检测，从而降低整个检测过程的时间复杂度。所以在进行目标检测之前必须要对目标所占据的距离窗口起始位置PL和宽度S进行估计。

回波信号与参考信号进行匹配滤波之后的一维距离像上，数据可以用离散形式表示为q(n)，n=1,2,…,N，假设目标所在的距离窗口为[PL,PR]，其中PR为终结位置，则窗口宽度为

S=PR-PL+1

(4)

由于目标的径向长度在不同的运动姿态下会变化，可以预估其变化范围为[lmin,lmax]，所以窗口宽度S也会与目标变化的径向长度匹配，当雷达距离分辨率为ΔR时，满足

(5)

假设目标所在窗口之外的距离元上全部为噪声，对匹配滤波值做平方率检波后，定义目标的广义信噪比(GSNR)为目标平均能量与噪声平均能量之比：

(6)

其中S满足式(5)，PL满足1≤PL≤N-S。

采取最大广义信噪比准则，当使得函数GSNR(PL,S)在约束条件下达到最大值时即可同时得到PL和S的最佳估计，即

(7)

通过约束条件下二维网格搜索即可得到上述目标函数的最优解。图2所示为基于最大广义信噪比准则的距离扩展窗口估计的性能曲线。由图可知，信噪比越大，窗口参数估计的准确率越高，当信噪比大于5 dB时，目标距离扩展窗口宽度越大，估计的准确率越高。以窗口宽度S=12时进行分析，当信噪比为5 dB时，该方法的估计准确率能达到63.42%，当信噪比为11 dB时估计准确率可达90.18%，当信噪比为20 dB时估计准确率可达99%。仿真结果表明了该方法的有效性和较高的估计性能。

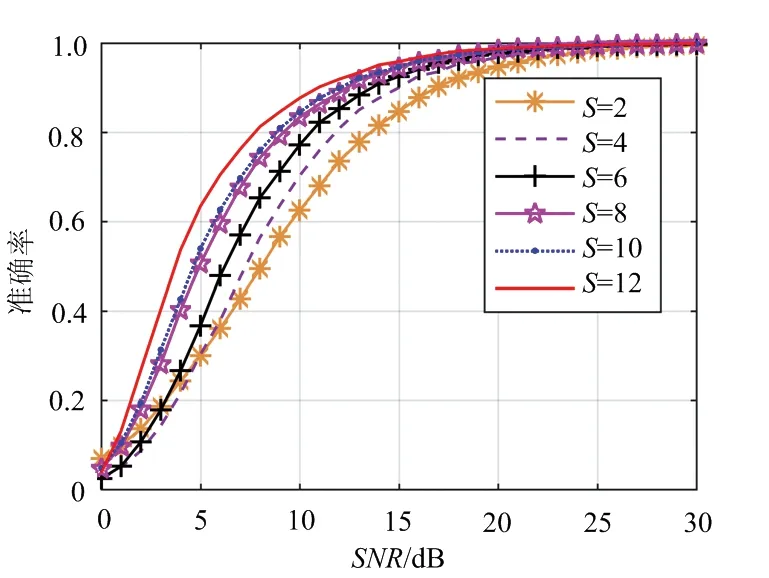
图2 基于最大广义信噪比准则的窗口参数估计算法性能曲线

3 距离扩展目标CFAR检测算法

3.1 二进制积累CFAR算法

二进制积累CFAR是一种经典的距离扩展目标检测算法，也叫L/S检测或双门限检测。当目标回波能量分布在连续的S个距离单元上时，采用宽度为S的距离维滑窗，先使用常规点目标CFAR检测算法对窗口内每个距离单元进行第一次门限检测，再对第一次检测结果进行二进制积累后进行第二次门限检测，第二次检测门限为L，即当第一次门限检测中有至少L次检测成功时，判定该连续的距离单元上存在距离扩展目标，否则无目标[4]。基于窗口参数估计的二进制积累CFAR流程图如图3所示，首先在RD谱上进行距离扩展窗口参数估计，得到窗口的起始位置和宽度，然后在该窗口内进行二进制积累CFAR检测判断窗口内是否为距离扩展目标。

图3 基于窗口参数估计的二进制积累CFAR算法流程图

3.2 模糊CFAR算法

文献[9]提出模糊检测算法的隶属函数，其将观测空间映射到一个0和1之间的值，表示“无信号”和“有信号”假设成立的程度。距离扩展目标的模糊CFAR检测算法即利用隶属函数的思想，将宽度为S的距离维滑窗内各距离单元值xi，(i=1,2,…,S)转换成映射到虚警空间的模糊隶属函数值ω(xi)，然后采用合适的积累准则对滑窗内的所有隶属函数值进行积累，得到该窗口的检测统计量[10]，最后与检测门限比较判决距离扩展目标是否存在。

在采取模糊OS-CFAR检测器时，隶属函数定义如下：

ω(x)=Pr(X>x|H0)=1-FX(x)

(8)

式中，x=qcut/z，qcut为待检单元，z为参考单元排序后的第k个元素值，X为x对应的随机变量，FX(x)是X的分布函数。所以ω(x)为单调递减函数，且均匀分布在[0,1]，当ω(x)=1时，表示无目标，当ω(x)=0时，表示检测到目标。

高斯背景下，参考单元个数为N时，OS-CFAR的虚警概率pfa和检测门限因子T关系[11]如下式所示：

(9)

将式(9)中的T用x代替，就可以得到高斯背景下模糊OS-CFAR的隶属函数：

(10)

首先在RD谱上进行距离扩展窗口参数估计，得到窗口的起始位置和宽度，然后对窗口内的所有单元值通过式(10)得到每个单元对应的模糊隶属函数值，最后通过积累准则得到检测统计量，当检测统计量小于门限TF时，即判定存在距离扩展目标，反之无目标。

图与Tabs关系曲线

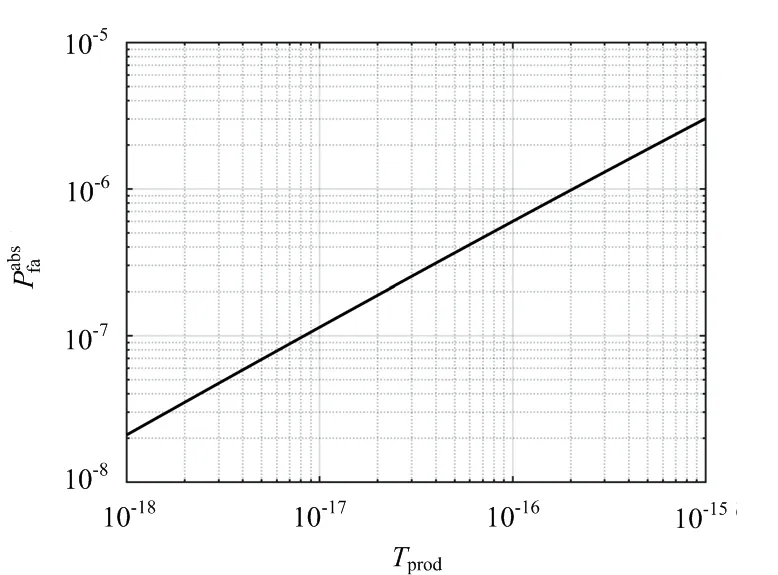
图与Tprod关系曲线

图与Tams关系曲线

模糊CFAR的积累准则主要有模糊代数和与模糊代数积两种[5]，文献[6]又提出了模糊算数和积累准则，下面将给出每种积累准则下模糊OS-CFAR的检测统计量以及目标不存在时虚警概率和检测门限的关系。并且给出了当目标所占距离元个数S为12时三种积累准则的虚警概率与检测门限的关系分别如图4，5，6所示，可知检测门限只与虚警概率有关，因此是恒虚警的。基于窗口参数估计的模糊OS-CFAR检测算法流程图如图7所示。

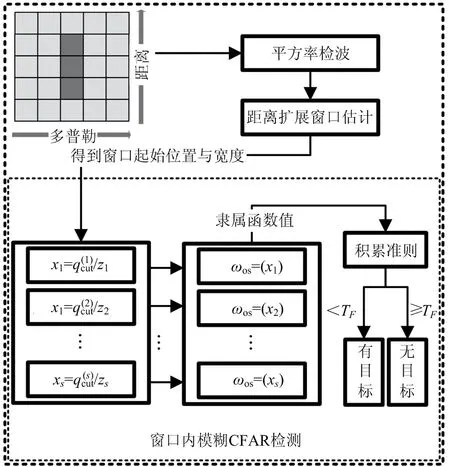
图7 基于窗口参数估计的模糊OS-CFAR算法流程图

3.2.1 模糊代数和

模糊代数和积累准则的检测统计量为

(11)

(12)

3.2.2 模糊代数积

模糊代数积积累准则的检测统计量为

(13)

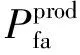
(14)

3.2.3 模糊算数和

模糊算数和积累准则的检测统计量为

(15)

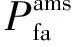
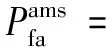
(16)

以上分析的是高斯背景下模糊OS-CFAR的三种积累准则的虚警概率和检测门限的关系式，实际上，服从其他噪声模型下的模糊OS-CFAR在三种积累准则下的检测门限与虚警概率的关系式也为式(12)、(14)、(16)，这是因为在模糊CFAR中，不论服从何种噪声模型，尽管隶属函数ω(x)表达式不同，但是ω(x)在区间[0,1]上始终服从均匀分布[6]，所以最终推导出的模糊CFAR的门限表达式都是相同的。

4 性能仿真

本节利用第1节建立的外辐射源雷达距离扩展目标回波模型表达式(3)，在高斯背景下仿真不同起伏模型[12]的距离扩展目标来对前述几种CFAR算法进行性能仿真。如图8是根据该模型仿真的一个连续占据12个距离单元的Swerling Ⅳ型目标，信号载频为786 MHz，带宽7.56 MHz，目标速度为-0.3 m/s，散射中心分布在第[20,31]个距离单元上。

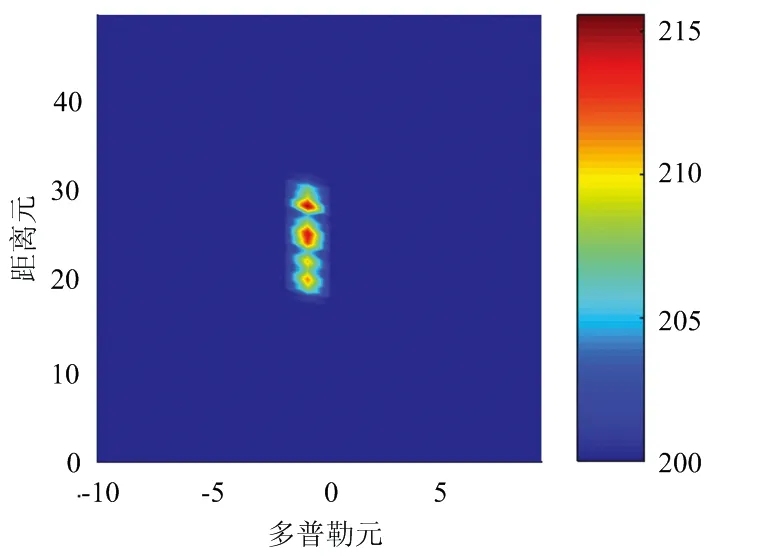
图8 仿真目标RD谱

仿真目标的一维距离像如图9所示，匹配滤波之后可以看到在距离维上出现了能量连续占据了12个距离元的距离扩展目标，证明了该回波模型的正确性。

图9 仿真目标一维距离像

利用Monte-Carlo方法进行距离维目标检测仿真实验，在高斯背景下，比较不同起伏目标模型下第一检测门限检测器为OS-CFAR的二进制积累CFAR算法和三种积累准则情况下的模糊OS-CFAR算法的检测性能。Monte-Carlo仿真次数为105，仿真参数如下：距离维参考窗长度N为24，OS-CFAR中的序值k为18，目标所占的距离单元数S为12，保护窗长度P为24，给定虚警概率Pfa为10-6，L/S算法采用7/12二进制积累准则。

4.1 Swerling Ⅱ型起伏目标

根据建立的扩展目标回波模型，采用目标散射点平均分布在整个距离滑窗内的Swerling Ⅱ型目标模型生成距离扩展目标回波，并与参考信号进行匹配滤波处理，经过平方率检波后在距离维上进行检测。

图10是均匀噪声环境下不同的检测算法的检测性能仿真结果。可以得出，在均匀噪声环境下，基于OS-CFAR的二进制积累CFAR和模糊CFAR算法都能有效地对Swerling Ⅱ型起伏模型的距离扩展目标进行检测，其中基于模糊代数积的模糊CFAR算法的检测性能最优，随着信噪比的增大，另外三种检测算法的检测性能曲线互有交叉点，当信噪比超过5 dB时，基于模糊代数和积累的模糊CFAR与二进制积累CFAR算法的性能相近，而基于模糊算数和的模糊CFAR算法性能最差。以检测概率Pd=0.5时为例，模糊代数积、模糊代数和、二进制积累和模糊算数和这四种CFAR算法所需的信噪比分别为4，6，6.5和7.5 dB，表明在相同的检测条件下，对Swerling Ⅱ型距离扩展目标的检测采取基于模糊代数积的模糊CFAR检测算法最佳，相比其他检测算法分别能得到2，2.5和3.5 dB的性能提升。

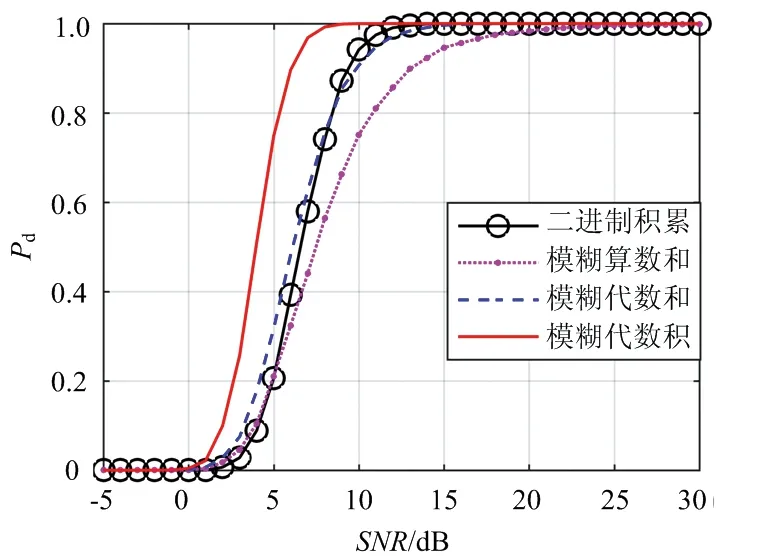
图10 均匀噪声环境下Swerling Ⅱ起伏目标不同检测算法性能比较

图11 多目标环境下Swerling Ⅱ起伏目标不同检测算法性能比较

图11是多目标环境(目标和干扰目标同时存在)下不同的检测算法的检测性能仿真结果，其中干扰目标的尺寸和功率等参数与待检目标完全相同，并在待检目标的前半参考窗内。

从仿真结果可以得出，在多目标环境下，基于OS-CFAR的二进制积累CFAR和基于模糊代数积的模糊CFAR算法都能有效地对Swerling Ⅱ型起伏模型的距离扩展目标进行检测，且基于模糊代数积的模糊CFAR性能最好，而基于模糊算数和与模糊代数和的模糊CFAR算法性能严重恶化，不适用于距离扩展目标检测。以检测概率Pd=0.5时为例，模糊代数积、二进制积累这两种CFAR算法所需的信噪比分别为7.4 dB、12.1 dB，表明在相同的检测条件下，对Swerling Ⅱ型距离扩展目标的检测采取基于模糊代数积的模糊CFAR检测算法最佳。

4.2 Swerling Ⅳ型起伏目标

采用目标散射点平均分布在整个距离滑窗内的Swerling Ⅳ型目标模型，与4.1节仿真处理过程相同，得到如图12所示的均匀噪声环境下不同检测算法的检测性能仿真结果。

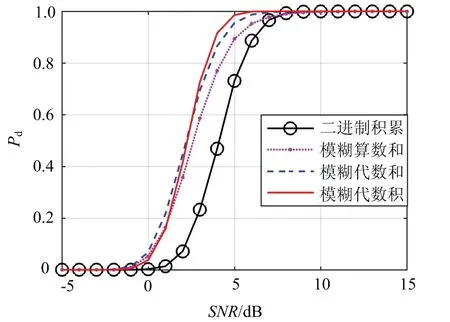
图12 均匀噪声环境下Swerling Ⅳ起伏目标不同检测算法性能比较

从仿真结果可以得出，在均匀噪声环境下，基于OS-CFAR的二进制积累CFAR和模糊CFAR算法都能有效地对Swerling Ⅳ型起伏模型的距离扩展目标进行检测，三种积累准则下的模糊CFAR算法检测性能接近，且均优于二进制积累CFAR算法。以检测概率Pd=0.5时为例，基于模糊代数积、模糊代数和、模糊算数和积累的模糊CFAR和二进制积累CFAR这四种检测算法所需的信噪比分别为2.2，2.18，2.6和4.2 dB，表明在相同的检测条件下，对Swerling Ⅳ型距离扩展目标的检测采取不同积累准则的CFAR检测算法均可以实现较好的检测性能，且均优于二进制积累CFAR。从图12中还可以看出基于模糊代数积积累的模糊CFAR检测出目标所需的信噪比最低，所以在实际情况下，为了达到最高检测概率，应选择基于模糊代数积积累的模糊CFAR算法。

图13是多目标环境(目标和干扰目标同时存在)下不同的检测算法的检测性能仿真结果，其中干扰目标的尺寸和功率等参数与待检目标完全相同，并在待检目标的前半参考窗内。

图13 多目标环境下Swerling Ⅳ起伏目标不同检测算法性能比较

从仿真结果可以得出，在多目标环境下，基于OS-CFAR的二进制积累CFAR和基于模糊代数积的模糊CFAR算法都能有效地对Swerling Ⅳ型起伏模型的距离扩展目标进行检测，且基于模糊代数积的模糊CFAR性能最好，而基于模糊算数和与模糊代数和的模糊CFAR算法性能严重恶化，不适用于距离扩展目标检测。以检测概率Pd=0.5时为例，模糊代数积、二进制积累这两种CFAR算法所需的信噪比分别为6.8 dB、11.3 dB，表明在相同的检测条件下，对Swerling Ⅳ型距离扩展目标的检测采取基于模糊代数积的模糊CFAR检测算法最佳。

5 实测数据处理

利用多通道数字电视外辐射源雷达系统在某海岸线开展了海上舰船目标探测实验，所利用的第三方辐射源频率为626 MHz，带宽为7.56 MHz。

5.1 目标距离扩展窗口估计

将实测数据进行参考信号重构[13]和杂波抑制[14-15]后进行匹配滤波处理得到RD谱如图14所示，如图中红色方框标注的为一距离扩展舰船目标，图15中给出了其所在的多普勒元对应的距离谱。为了验证前述距离扩展目标检测算法的性能，首先需要估计目标所占据的距离扩展窗口的位置和宽度。

图14 实测目标RD谱

采用第2节提出的最大广义信噪比准则的距离扩展窗口参数估计方法对图15所示的距离谱进行估计，通过约束条件下的二维网格搜索得到目标距离扩展窗口宽度最优解为11，起始位置最优解为第186个距离单元，所以目标能量分布在[186,196]距离单元上，提取出该目标的一维距离像如图16所示。

图15 目标所在多普勒元的距离谱

图16 实测目标的一维距离像

5.2 实测数据实验验证

对上面提取到的舰船目标一维距离像添加不同信噪比的高斯噪声，信噪比范围为[0,20 dB]，采取第4节中使用的CFAR算法进行目标检测，其中二进制积累CFAR采取6/11准则。每个信噪比进行105次Monte-Carlo仿真，得到四种CFAR算法的检测性能曲线如图17所示。

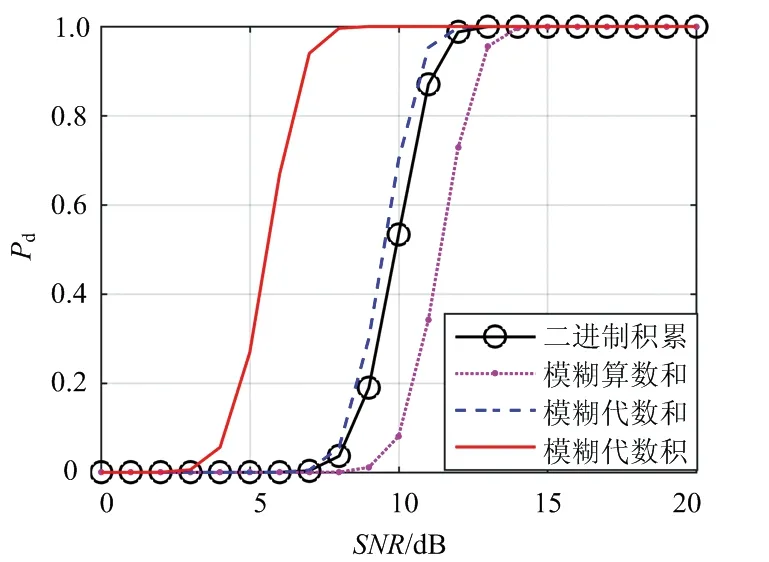
图17 该目标下不同检测算法性能比较

从图中可知在该实测目标下，基于模糊代数积积累的模糊CFAR检测性能最好，基于模糊代数和积累的模糊CFAR与二进制积累CFAR的检测性能接近，基于模糊算数和积累准则的模糊CFAR检测性能最差，这与Swerling Ⅱ型目标的检测性能仿真结果较为符合。以检测概率Pd=0.5时为例，模糊代数积、模糊代数和、二进制积累和模糊算数和这四种CFAR算法所需的信噪比分别为5.5，9.5，9.58和11.3 dB，基于模糊代数积积累的模糊CFAR相比其他检测算法分别能得到4，4.08和5.8 dB的性能提升。由于实际情况下探测到的目标受到各种因素影响，如舰船的运行姿态、海浪波动和雷达系统的精度，使得距离扩展目标各散射中心的回波强度有不同程度的损失，会给检测性能带来一定损失。

6 结束语

本文研究了距离扩展目标检测算法，以外辐射源雷达为背景，建立了距离扩展目标回波模型，提出了基于最大广义信噪比准则的距离扩展窗口参数估计方法，该方法能有效估计出窗口的位置和宽度，然后研究了距离扩展窗口内目标的二进制积累CFAR，以及模糊代数积、模糊代数和和模糊算数和这三种积累准则下的模糊CFAR检测算法，最后对外辐射源雷达舰船目标探测的实测数据进行处理。结果表明在均匀噪声环境下和多目标环境下，目标服从Swerling Ⅱ型起伏模型和Swerling Ⅳ型起伏模型时，在距离扩展窗口内采取基于模糊代数积积累的模糊CFAR检测性能均最优。实测数据也证明了基于模糊代数积积累的模糊CFAR检测性能最优。

后续将针对外辐射源雷达具体的应用环境，研究其他模糊CFAR算法，如将均值类CFAR用于第一门限中。