教师在圆锥曲线教学中的隐蔽错误及其反思

王淼生

（厦门第一中学，福建 厦门 361003）

笔者曾归纳了学生在解答三角、立体几何、线性规划等知识模块试题中常见的典型错误及应对策略.［1］圆锥曲线在高中数学中占有极其重要的地位，其本质就是渗透数形结合思想，是高考、竞赛中的重点、热点、难点.圆锥曲线相关试题知识点多、计算量大、推理过程繁、变形技巧高、解答灵活性强、思维跨越度大，导致学生出现这样或那样的瑕疵乃至错误.其实，错误不是学生“专利”.教师在圆锥曲线的精致概念、解题过程、命制试题、改编试题中也会类似瑕疵乃至错误，有些错误极其隐蔽，甚至个别问题至今都难以圆满解决.减少乃至杜绝这些错误是一线教师必须面对的课题.

一、精致概念出现茫然

案例1：若椭圆焦点为F1（9,20）、F2(49,55)，且与x轴相切，则该椭圆长轴长的最小值为_____________.

错解：案例1 为某地青年教师解题大赛试题.由于教材是在标准状态下呈现圆锥曲线方程（即标准方程），因而不少教师看到焦点不在x轴或y轴，心生畏惧而放弃，还有不少教师没有悟透概念（椭圆定义）更不会精致概念而茫然无措.

错因：数学教学中最困难、最棘手的就是概念教学，数学概念是进行推理、判断、证明的依据，是构建定理、法则、公式的基础，是建立数学知识体系的根基，是形成数学思想方法的源泉，是解决数学问题的前提.数学教学核心就是概念教学，关键在于精致概念，这是考量教师专业功底的重要标志.需要教师在概念产生、生成过程中明晰概念来龙去脉，在体验概念引入、发展进程中辨析概念，在概念的归纳、提炼历程中巩固概念，在构建、甄别概念动态过程中精致概念.教科书是这样给出椭圆定义：

平面上动点p到两个定点F1、F2距离之和为定值2a，且2a＞2c=此时动点P的轨迹是以定点F1、F2为焦点、2a为长轴长的椭圆.当我们以定点F1、F2所在直线为x轴，线段F1F2中垂线为y轴建立平面直角坐标系时，得到椭圆方程为=1.其实可以任意建系.当然，不同建系方式，得到椭圆方程是不同的.只不过将焦点放在x轴或y轴时得到的方程最为简单，故而称为标准方程.进一步精致椭圆定义得到：无论以何种方式建立直角坐标系，其轨迹都是椭圆，且只要动点P在椭圆上运动，恒有|PF1|+|PF2|=2a.据此得到以下正确解答：

二、强行计算出现失利

案例2：双曲线中心为原点，焦点在x轴上，渐近线分别为l1，l2，经过右焦点F且垂直于l1的直线l分别交l1，l2于A，B.若成等差数列，与同向.［2］

（I）求双曲线的离心率；（II）设AB被双曲线所截得的线段长为4，求双曲线方程.

案例2 为2018 年高考全国I 卷文科第22 题（理科第21 题）.通过双曲线这一载体，考查解析几何基本思想、基本方法，涉及数形结合、转化与化归、方程等思想，是一道经典试题，因此某地将上述案例2 第（I）问改为填空题并作为参加某省技能大赛测试题.案例2 入手不难，遗憾的是在规定时间内完整解答出来的选手寥寥无几.

错解：设出直线l的方程并分别与l1，l2联立求出A，B坐标，再依据两点间距离公式求出，最后强行代入2看似目标明确，但因字母较多，运算量很大，加上时间紧张、心理压力大，最终无功而返.

错因：计算不同于运算，这正是将数学运算作为六大核心素养之一的缘由.渐近线作为双曲线特有标志，具有独特性质.尤其要掌握过焦点作渐近线垂线所涉及的结论，有利于理解运算对象，掌握运算法则，探究运算方向，选择运算方法，设计运算程序，求出运算结果，反思运算历程，提升数学运算素养.

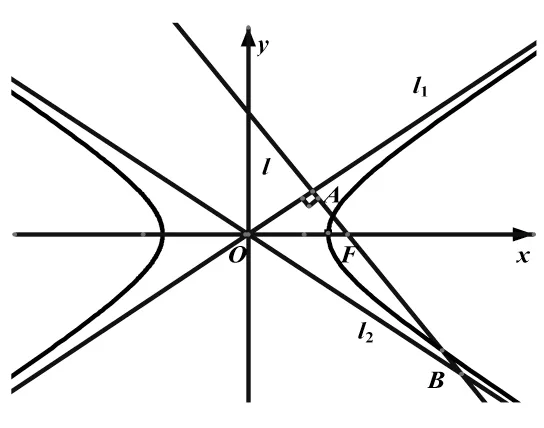
图1

三、解答试题出现偏差

错因：案例3 是某地高三模拟试题.上述解答过程流畅，似乎无懈可击，其实不然.由上述等号成立的条件便知m=n，且2β=，则△PF1F2为等腰直角三角形，即b=c（c为半焦距）.也就是说，当点P位于椭圆短轴顶点且b=c时取得最大值.事实上，案例3中的条件并没有必须保证具备b=c，因而上述解法实际上人为加强了条件而导致错误.

正解：由上述错解过程及余弦定理可得

当且仅当m=n，即当点P位于椭圆短轴顶点时取得最大值.

解析几何最值问题经常借助基本不等式求解.但多次使用基本不等式要保证每一次等号成立的条件和谐相处，尤其当基本不等式与三角同时进行放缩时，更要慎重检验放缩过程是否与题意保持一致，是否忠实于原题要求，否则会出现意想不到的错误.

四、命制试题出现错误

图2

错因：案例4 源自某地考题.上述求解、推理看似严谨、规范，但这确实是一道错题.原因在于满足条件的点P根本不存在.而上述解答过程是在默认点P存在的前提下而得到.

由此说明直线F1P与这条渐近线平行，这就意味着直线F1P与双曲线右支根本不可能相交，从而说明这样的点P不存在，当然△PF1F2就不存在.

修复：要使这样的△PF1F2存在，只要使得kF1P＜k1，比如，已知“直线IF1的斜率为”就存在这样的△PF1F2，依据上述解答方法可以求出相应的△PF1F2的内切圆的方程.

五、改编试题出现瑕疵

上式即为动点P的轨迹方程，因此动点P的轨迹为椭圆（去掉A，B）.

同理，设Q(x,y)，依据已知条件可得

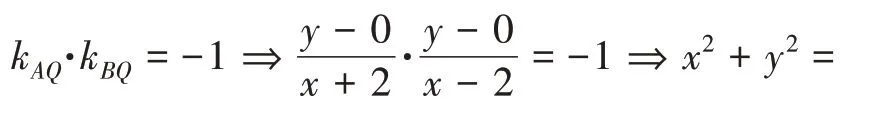
图3

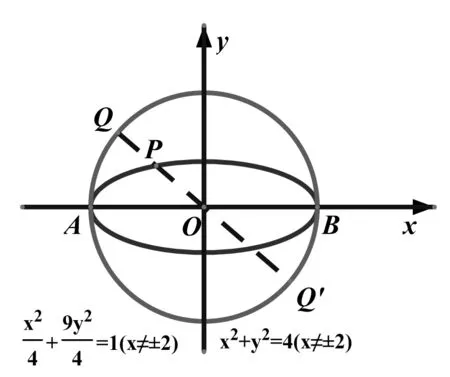
图4

错因：案例5 源自某地高三质检题.以向量为载体，考查圆、椭圆及最值、范围，凸显数形结合、转化化归等思想，是一道集知识、能力、方法、思想及素养于一体的综合性较强试题.从局部看，上述解答每一步似乎都是严谨、规范的，但从整体审视，确实存在瑕疵，甚至错误，而且极其隐蔽.［1］那到底错在哪儿呢？是解答错误还是试题本身有瑕疵呢？

为了便于说明问题，以下将原题摘录如下：

案例6：设点A，B的坐标分别为(-5,0)，(5,0).直线AM，BM相交于点M，且它们的斜率之积为-，求点M的轨迹方程.

案例6 事先设置了点的坐标，因此其轨迹与方程是唯一确定的.然而，上述解答过程中的建系是将线段AB所在直线为x轴，也就是说，解答中得到的椭圆=1 是长轴最短的椭圆（如图5）.倘若将线段AB所在直线为y轴，那么得到的椭圆就是长轴最长的椭圆（如图6），这就说明案例5 中的椭圆是一个不确定的椭圆.

图5

图6

事实上，线段AB不一定必须作为椭圆长轴.将线段AB作为椭圆任意一条中心弦都可以满足斜率之积为定值.也就是说，上述解答正是在长轴最短的椭圆下得到的答案，显然是不严谨的.为了更加直观地说明问题，利用几何画板绘出以下图形：

以|PQ|最小值为例：图7 就是长轴最短的椭圆，此时|PQ|min≈0.85；图8 就是长轴最长的椭圆，此时≈0.90.由此说明不同建系得到的最小值是不同的！至此，可以判定上述解答过程是错误的.遗憾的是，因笔者功底浅薄，至今还有一些疑惑：如果案例5 正确，那么| |PQ取值范围到底是什么？如果案例5本身存在瑕疵，瑕疵在哪儿？又该如何修复？以后命制此类试题时如何避免犯同样错误？

图7

图8

罗增儒教授认为，错误是越过障碍、达到目标的必经阶段；错误是接受洗礼、走向成熟的必要磨炼.［3］错误是一面镜子，能够充分暴露解题人、命题人的构思历程、思维过程，同时错误也是难得的、宝贵的教学资源，深刻反思出现错误的诱因、出现错误的方式以及矫正错误的良策，拨乱反正，走出误区，在“错”中“磋”、在“误”中“悟”、在“探”中“叹”.