基于CPSOGSA的水轮机调速系统PID参数优化

贾高杰，钱 晶，2，邹屹东，曾 云，2

（1.昆明理工大学冶金与能源工程学院；2.云南省高校水力机械智能测试工程研究中心，云南昆明 650093）

0 引言

调速系统的PID（Proportional，Integral，Differential）参数优化是影响水力发电机组性能的关键环节，对该参数进行合理选择不仅可以确保机组安全稳定运行［1］，还能抑制电网扰动诱发的全网超低频振荡现象［2-3］，具有重要现实意义。

水轮机调速器是水轮发电机组非常重要的辅助控制设备，随着计算机技术和控制理论的飞速发展，目前已有多种优化算法被应用于水轮机调速器的参数优化中［4］。水电机组并网后一般采用一组PID 控制参数，而采用固定的控制参数难以保证不同工况下均具有良好的动态性能。为此，文献［5］提出一种基于Chebyshev 融合狼群协同围攻策略的改进灰狼优化算法，在求解不同维度的基准测试函数上具有更好的寻优性和稳定性；文献［6］提出在脉冲负载条件下，模糊PID 调速系统相较于常规PID 调速系统有更好的实时调节性能，能够较好地改善系统电能质量；文献［7］提出一种改进萤火虫算法，在不同工况下均能发挥较好的调节功能；文献［8］提出一种分数阶PID（Fractional Order PID，FOPID）控制策略，对含有非线性环节的系统具有更好的控制效果，表现出较强的鲁棒稳定性；文献［9］提出一种概率统计Bayes 公式与MAXQ 算法相结合的自适应行为预测算法B-MAXQ（Bayes-MAXQ），对调速器的PID参数进行预测；文献［10］提出一种基于遗传算法的模糊PID 控制系统，能够对永磁同步调速系统进行有效控制，进而使系统具有较优异的起动特性和动态稳定性；文献［11］提出一种基于模糊神经网络的水轮机调速器PID 参数控制策略，弥补了传统PID 控制鲁棒性和自适应能力较差的劣势，提高了水轮机组的控制性能。

然而，上述算法在全局搜索能力上存在局限性，普遍存在早熟收敛的问题，容易陷入局部最优化。收敛因子粒子群优化（Constriction Coefficient Particle Swarm Optimization，CPSO）算法收敛速度快，且陷入局部最小值的可能性较小［12］。引力搜索算法（Gravitational Search Algorithm，GSA）需要的预设值少，且同时考虑到了解的质量和适应度值［13］。本文将两者结合起来建立CPSOGSA 算法，应用于水轮机调速系统的智能控制中，以优化神经网络模型参数［14］并确定最小二乘支持向量回归（Least Square Support Vector Regression，LSSVR）的最优参数［15］。

1 水轮机调速系统模型建立

采用IEEE Working Group 在分析总结水轮机模型研究基础提出的非线性模型［16］。模型的非线性主要体现在水力系统动态的非线性描述和出力代数方程的非线性形式上，即主要通过水轮机水头和流量的变化体现，水头与流量为非线性关系，因此水轮机出力是水轮机水头和流量的非线性函数。水轮机出力、流量、水头的表达式分别为：

水力系统的动态，即水轮机水头的暂态变化采用非线性微分方程描述，水轮机引水系统流量变化到水头变化的传递函数为：

式中，Zn为管道的水力浪涌阻抗系数；Te为水力弹性时间；s为拉普拉斯算子。

本文采用单机单管的水力系统，并采用传递函数为简单刚性水击模型，即上述公式中n=0的情形。

目前水电站中使用最广泛的微机调速器为典型的并联PID 控制单元，电液随动系统采用一阶惯性环节，两者的传递函数为：

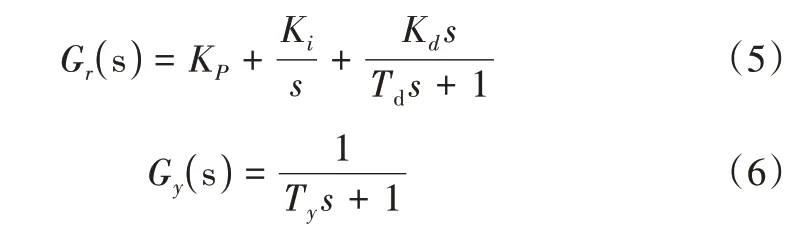
式中，Kp、Ki、Kd分别为PID 调节器的比例、积分、微分增益系数。

在水轮机调速系统仿真研究实验中，将一阶发电机简化模型与水轮机模型及PID 控制规律结合，采用MATLAB/Simulink 仿真实验平台以两路并联模块的形式建立水轮机调速系统的非线性仿真模型，如图1 所示。对该仿真模型作以下说明：①传递函数为增量线性化模型，用于描述非线性特性时涉及初值的设定，例如y0、q0、h0、mg0、mt0等可通过预设初值的形式表达；②时间乘以误差值绝对积分（Integral of Time and Absolute Error，ITAE）是衡量算法优劣的性能指标，以控制量、误差和时间为约束条件；③频率扰动通过预设阶跃信号实现，图1 中的风电功率扰动通过mg0输入扰动模拟。

2 基于CPSOGSA的PID设计

2.1 CPSO算法

经典粒子群优化算法（Particle Swarm Optimization，PSO）由3 个重要的算子组成，分别为惯性权重ω、个体最佳粒子pbest和全局最佳粒子gbest［17］，其中惯性权重ω 为PSO 提供了多样化探索能力和强化开发能力［18］。动态ω能获得比固定值更好的寻优结果［19］，其可在PSO 搜索过程中线性变化，也可以根据PSO 性能的某个测度函数动态改变［20］，目前采用较多的为线性递减权值（Linearly Decreasing Weight，LDW）策略。

粒子群的速度和位置分别表示为：

CPSO 算法对经典PSO 算法进行了严格的代数和特征值搜索过程分析，控制粒子从搜索空间向外移动，从而增加粒子向pbest和gbest的收敛速度。各类控制参数分别表示为：

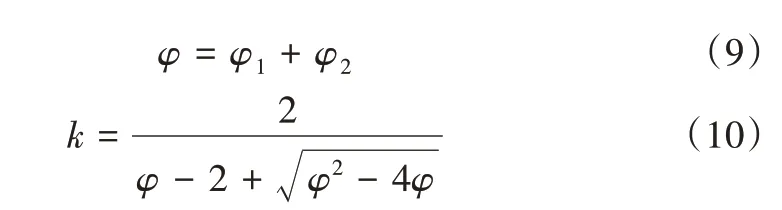
式中，φ1、φ2、φ均为控制参数，其值对于控制粒子轨迹非常重要；k为收缩因子，其对于粒子收敛至全局最优值至关重要。

当ω（t）=k、C1=k×φ1和C2=k×φ2时，修正形式的速度公式表示为：

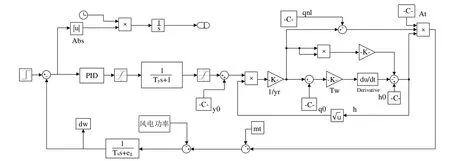
Fig.1 Simulation model of nonlinear hydraulic turbine speed control system图1 非线性水轮机调速系统仿真模型

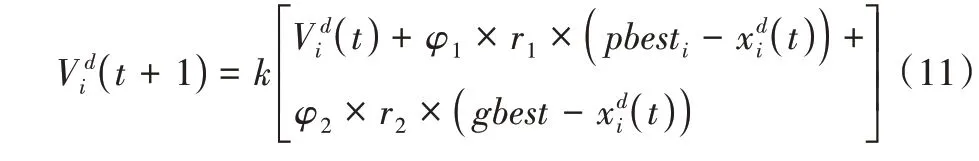
可以看出，粒子的速度V与控制参数φ成反比。为了保持系统的稳定性，φ值必须大于4。

2.2 GSA算法

GSA 算法中，每个质量代理都有位置、惯性质量、主动引力质量和被动引力质量4 个属性。随着时间的推移，质量期望会被最大质量吸引，而这个最大质量表示搜索空间中的一个最优解。

假设1个系统有N个代理，其中第i个代理的位置被定义为：

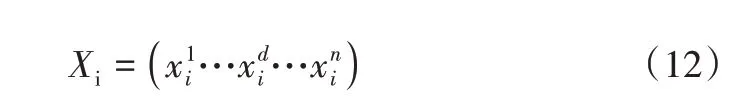
根据引力理论，将质量j作用于质量i，在t次迭代时的计算公式为：

式中，Mj为代理质量j的主动引力质量，Mi为代理质量i的被动引力质量，G（t）为t次迭代的引力常量。每个代理的惯性质量计算方式为：

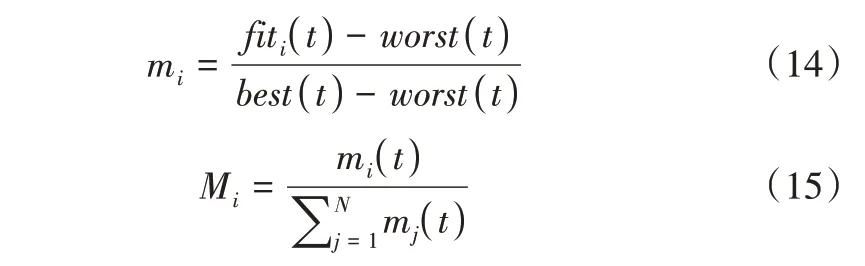
式中，fit（it）表示代理i在t次迭代时的适应度值，best（t）和wors（tt）分别表示所有代理的最优值和最差值。

代理i在维度d受到的总重力表示为：

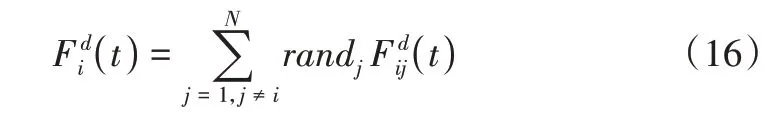
式中，randj表示0～1之间的随机数。

代理i在t次迭代，第d维空间上的加速度为：

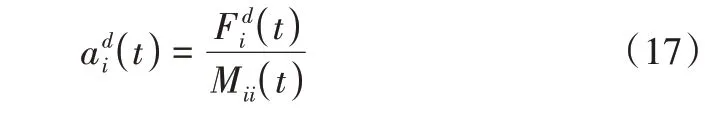
式中，M（iit）对应代理i的质量。

代理i的下一个速度为当前速度加上其加速度，得到的速度和位置分别为：

2.3 CPSOGSA算法

CPSOGSA 算法的主要目标是基于GSA 算法的搜索能力和CPSO 算法的收敛能力，同时利用混沌映射克服标准GSA 算法局部极小值问题中的陷阱。两种算法的合并方程为：

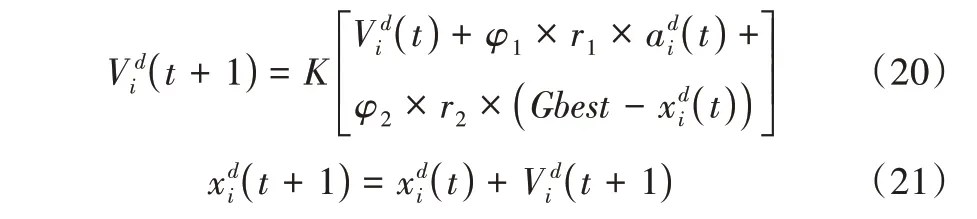
式中，V（it）表示记忆项，r1和r2表示0～1 之间的两个随机数，Gbest 表示全局最优解，ai表示加速度，xi表示i当前位置。

3 优化流程

3.1 评价函数

在系统迭代过程中，根据系统输出响应的超调量、上升时间、调节时间和稳态误差等判断控制性能优劣。使用综合时间与绝对误差（ITAE）作为算法的评价函数，其是误差绝对值乘以时间项对时间的积分，既能体现出误差大小（控制精度），又能体现误差收敛速度，表示为：

3.2 PID参数优化流程

水电机组的PID 参数优化过程如图2 所示。由于确定工况下水轮机系统的传递系数是已知的，预设好算法的初值后，在MATLAB/Simulink 平台上得到仿真模型的输出数值，采用输出数值计算相对应的评价函数，仿真模型多次反复迭代直到满足循环次数，最后输出寻优结果。算法流程如图3所示。

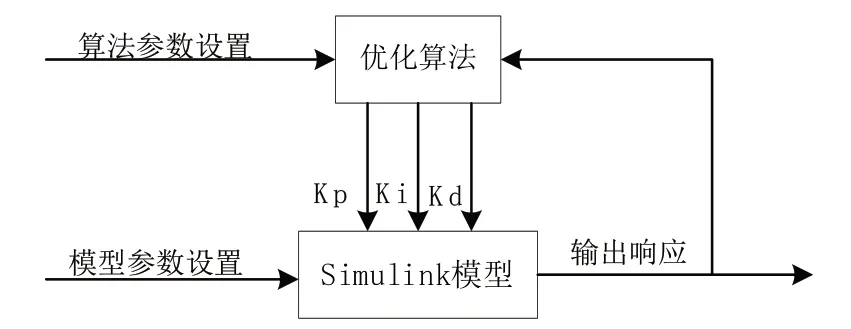
Fig.2 PID parameter optimization process图2 PID参数优化过程

Fig.3 Algorithm flow图3 算法流程

4 算例仿真计算

图4为水电—风电联合运行系统示意图。

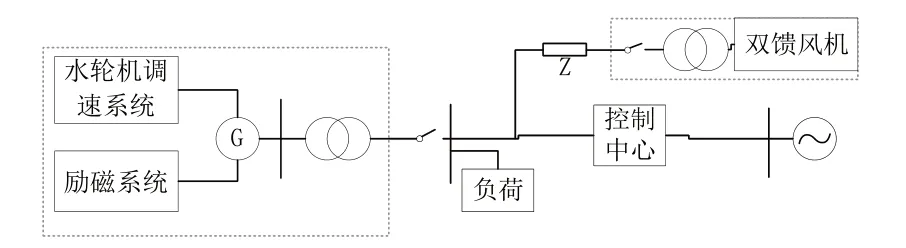
Fig.4 Hydropower-wind power joint operation system diagram图4 水电—风电联合运行系统

4.1 仿真参数

水轮机调速系统非线性模型仿真实验参数设定如表1所示。现有CPSOGSA 算法多为人为预设参数值，对于水轮机调节系统不具有普适性。本文经过大量仿真实验计算发现以下几个规律：①在系统仿真计算中，ITAE 指标数值与PSO 的适应度值fitness和GSA 的质量值mass有一定关系，一起进入算法循环后，fitness和mass数值设置得过大或过小均会影响CPSOGSA 算法的迭代寻优过程。fitenss=0.1 和mass=0.1 时可以较好地满足调节系统需要；②适当增加惯性权重ω或减小引力权重G有利于加快CPSOGSA算法的空间探索速度。φ1=2.05、φ2=2.05、G0=0.1 时能使CPSOGSA 算法在系统仿真计算中的迭代次数减少，加快收敛速度。

Table 1 Simulation parameters of hydraulic turbine model表1 水轮机模型仿真参数

CPSOGSA 算法其他仿真参数设置：维数d=3，栖息地个数N=50，迭代次数iteration=100，Kp∊［0，8］，Ki∊［0，4］，Kd∊［0，6］。

4.2 频率扰动工况

仿真实验在刚性水击模型的5%频率扰动工况下进行，仿真时间为30s。实验得到的评价函数适应度曲线如图5 所示，图中Iteration 为程序迭代次数，W为适应度值。可以看出，经CPSOGSA 算法改进后的适应度曲线在第9 次迭代就达到了0.7 以下的适应度值，在第25 次迭代后趋向于稳定，说明自26 次迭代后，评价函数就已经收敛并且达到了控制参数所要求的最优值。

Fig.5 Fitness curve under 5%frequency disturbance图5 5%频率扰动下适应度曲线

由图6 可以看出，CPSOGSA 算法超调量比常规PID 小5.6%，系统在10s 内便能趋于稳定，而常规PID 则需要在22s左右才能使系统稳定。

PID 参数及其对应的控制性能指标详见表2。可以看出，在5%频率扰动下，CPSOGSA 算法的Ki、Kd值均小于常规PID，但常规PID 的ITAE 指标却 比CPSOGSA 算法更大。

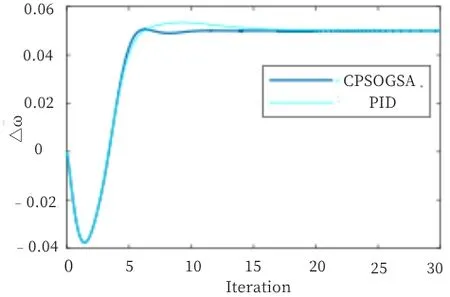
Fig.6 Comparison under 5%frequency disturbance图6 5%频率扰动下比较

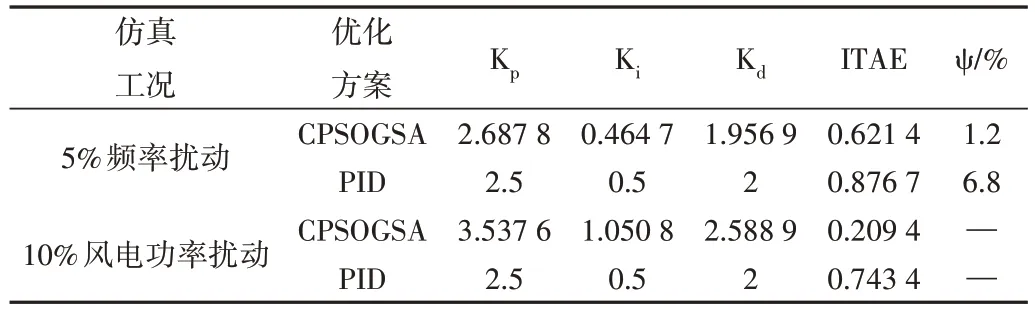
Table 2 Comparison of PID parameters and control performance indicators表2 PID参数及控制性能指标比较

4.3 风电功率扰动工况

第2 组仿真实验在刚性水击模型的10%风电功率扰动工况下进行，仿真时间为30s。图7 为恒定风速下模拟实际风电机组的风电功率输出曲线，得到的评价函数适应度曲线如图8所示。

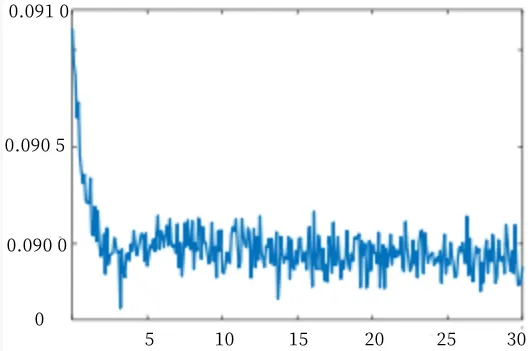
Fig.7 Wind power output curve图7 风电功率输出曲线

由图8 可以看出，CPSOGSA 算法在第8 次迭代时就达到了0.22 以下的适应度值，在第19 次迭代后趋向于稳定，说明自20 次迭代后，评价函数就已经收敛并且达到了仿真研究要求的最优适应度曲线。

由图9 可以看出，CPSOGSA 算法优化后的系统在12s内趋于稳定，而常规PID 下的系统运动轨迹近似于二次函数，经23s 才趋于稳定。由表2 可以看出，在10%风电功率扰动下，CPSOGSA 算法的Kp、Ki、Kd值均大于常规PID，但常规PID 的ITAE 指标却依旧比CPSOGSA 算法更大，说明后者的探索功能较优。

Fig.8 Fitness curve under 10%wind power disturbance图8 10%风电功率扰动下适应度曲线

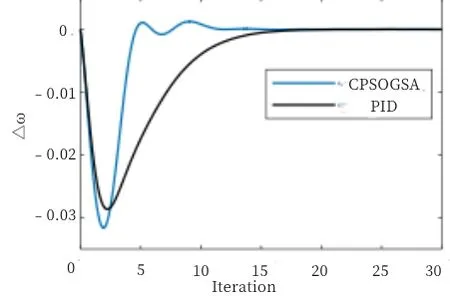
Fig.9 Comparison under 10%wind power disturbance图9 10%风电功率扰动下比较

5 结语

针对水轮机调节系统的非线性、时变性和多工况情况，本文提出一种基于CPSOGSA 算法的水轮机调速器PID参数控制策略，其将CPSO 和GSA 两种智能控制算法相结合，实时整定调速器PID 参数。仿真实验结果表明，相较于传统PID 控制策略，基于CPSOGSA 算法的水轮机系统动态性能较优，弥补了传统PID 控制鲁棒性和自适应能力较差的劣势，有效提高了水轮机组的控制性能。在后续工作中，将进一步研究在其他风电功率扰动工况下水轮机调节系统的PID 参数整定以及系统动态性能优化问题。