基于WOA-LightGBM的盾构切削锚杆参数预测

叶 飞，冯浩岚，梁 兴，刘 畅，梁晓明，张稳军

（1.长安大学公路学院，陕西西安 710064；2.天津大学建筑工程学院，天津 300350；3.天津大学滨海土木工程结构与安全教育部重点实验室，天津 300350）

随着盾构机在地铁工程中的广泛应用，其下穿建筑物的工况频发。在城市大规模规划及建设过程中，高层建筑物拔地而起，取代了较低的城市构筑物，在这些建筑物施工过程中，基坑的有效支护对施工安全有着重要的意义［1］。现阶段，最常用的基坑支护手段为桩锚支护。即在基坑周围施作一圈人工钻孔桩，桩间施作两到四层的预应力锚杆支护，从而对基坑外土体进行有力的支撑，防止土体失稳进入到基坑中。在基坑施工完成后，桩锚支护中的预应力锚杆将残留在地层中，为后续盾构隧道的施工埋下了隐患。在盾构施工过程中，为保证建筑物的安全，盾构机一般选择避开建筑物，从两边绕行，但由于基坑中的锚杆未被回收利用，仍埋在地层中。因此，盾构机在此区域内施工时，将会遇到残留地层锚杆，此即盾构机穿越锚固区的问题。此时，盾构机常采用滚刀来切削锚杆内钢筋与混凝土，以达到顺利破除锚杆的目的［2］。值得注意的是，盾构机在接触锚杆时，其掘进参数难以控制，如刀盘扭矩将会变大，贯入度将会变低，掘进效率及安全性得不到保证。根据相关文献以及现场施工人员的反馈，在掘进过程中，盾构机难以调节相关操作参数（如推力、螺旋输送机转速和刀盘转速等），来达到安全快速掘进的目标［3-5］。因此，根据地层内锚杆情况及盾构机的操作参数，如何对盾构机穿锚时的掘进性能进行精确预测是一个亟待解决的问题。

机器学习是一门交叉学科，在人工智能领域处于核心地位。自1950年，艾伦图灵构建了第一个学习机器起，迄今为止，机器学习已取得显著的进步［6］。根据不同的研究方向，不同的针对目标，世界上不同领域的学者研究提出了诸多关于机器学习的理论并加以实践［7-8］。在盾构领域内，诸多学者已尝试采用多种人工智能模型预测TBM的推进速度（AR）和贯入度（PR）等性能参数［9］，人工智能模型包括粒子群优化（PSO，particle swarm optimization），模糊逻辑（fuzzy logic），人工神经网络（ANN，artificial neural network），自适应神经模糊推理系统（ANFIS，adoptive neuro-fuzzy inference system）和帝国竞争算法（ICA，imperialist competitive algorithm）等。其中，Grima等［10］提出了一种ANFIS模型来预测贯入度，结果表明，ANFIS的预测结果比当时的统计方法更加准确。同时，Mahdevari等［11］提出了支持向量机回归模型（SVR）。Danial等［12］总结了人工智能在隧道工程和地下空间技术中的应用，并用人工智能模型评估了不同风化带下TBM的掘进性能。鲸鱼优化算法是一种新颖的、受自然启发的元启发式优化算法，可对机器学习模型中的超参数进行优化［13-14］。赵帅［15］采用鲸鱼优化算法解决了因人工设置参数而影响核极限学习机预测效果的问题，建立了KPCA-WOAKELM岩爆烈度预测模型。经海翔等［16］利用改进的鲸鱼优化算法优化了概率神经网络，提高了通风机故障诊断精度。

对于盾构机穿越锚固区的掘进性能预测问题，输入特征的选取是其是否具有参考意义的重要因素［17-20］。但是现仍未有相关文献对此问题进行过研究，更未建立起盾构穿锚的预测模型。因此，一套可成功预测盾构穿越锚固区掘进性能的预测模型亟需建立。轻量级梯度提升机（LightGBM）模型是近年来新提出的Boost框架下的算法，具有训练速度极快、占用内存小等优点，在盾构领域仍未广泛应用［21］。因此，本文将在分析锚固地层工程特性的基础上，建立一套盾构机穿锚预测模型，并依托武汉地铁工程，对实际盾构机穿锚参数进行实时收集。此外，鉴于LightGBM超参数众多，且人工调参具有很大的局限性，因此本文基于鲸鱼优化算法对LightGBM的超参数进行寻优，以寻得在数据集上的最优参数组合。同时将模型预测结果与传统BP神经网络、极限学习机（ELM）模型进行对比，验证该模型的准确率。

1 工程概况

武汉地铁8号线水果湖-洪山路区间线间距为8.0～15.2 m，隧道边最小距离为2 m，埋深11.5～13.7 m。现场调研发现，水果湖大厦锚杆形式为桩锚，即基坑由一排900 mm 的人工挖孔桩支护，且每根桩间设置上下两根锚杆，上层长为20 m，下层长为18 m。上下两排设计数量共计190组，每组锚杆由2根φ20或2根φ25的HRB400螺纹钢组成，设计俯角29°插入土体，如图1 和图2 所示。左线隧道155～233 环有锚杆侵入；右线隧道156～181 环有锚杆侵入。模拟平面投影影响区域为100×20 m；侵入隧道范围的锚杆总长约102 m。实际工程中盾构左线先掘进，通过此区域后盾构右线再进行掘进。

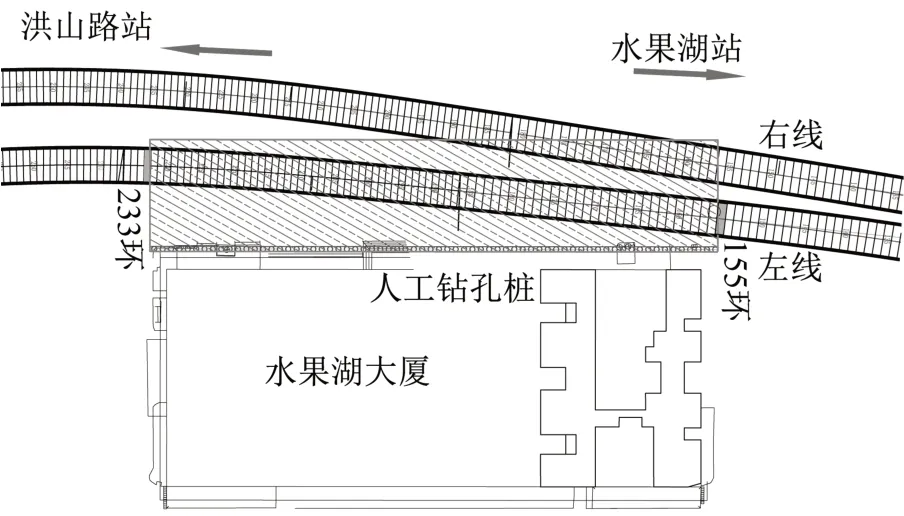
图1 锚杆侵入盾构区间平面图Fig.1 Simulated plane projection of anchorage area

图2 盾构掘进与锚杆的位置关系Fig.2 Position relationship between shield tunneling and anchor bolts

盾构机刀盘开口率约30%；千斤顶最大推力34 100 kN，最大掘进速度8.0 cm·min-1，刀盘的工作扭矩为4 474 kN·m。现场调研情况如图3 所示，锚杆由2 根直径为20 mm 或25 mm 的螺纹钢筋焊接而成，且由直径17 cm的混凝土包封包裹，混凝土包封强度为30～38 MPa。

图3 现场锚杆混凝土与钢筋Fig.3 Site diagram of anchor bolt

2 LightGBM智能预测模型构建

2.1 LightGBM算法概述

为了解决大数据下传统boosting 算法耗时长的缺点，Ke［21］提出了两种新技术：基于梯度的单侧采样技 术（GOSS）和 互 斥 特 征 捆 绑 算 法（EFB）。LightGBM（Light Gradient Boosting Machine）结合GOSS 和EFB，是一款基于决策树算法的分布式梯度提升框架。为了满足工业界缩短模型计算时间的需求，LightGBM的设计思路是减小数据对内存的使用，保证单个机器在不牺牲速度的情况下，尽可能地用上更多的数据；此外，减小通信的代价，提升多机并行时的效率，实现在计算上的线性加速。

2.2 输入特征选取

2.2.1锚固端头位置

为对相似穿锚工程提供操作参数的指导，首先需要确定此类盾构机穿锚工程的问题所在。一般而言，若地层内存在残留锚杆，盾构机一般选择侧穿建筑物。因此，本文针对盾构机侧穿建筑物问题进行探讨，分析了可指代锚固地层特征的相关工程指标，最终选取6 个工程指标作为后续模型的输入特征。首先，取一层侵入锚杆为例，由于锚杆与盾构机刀盘截面的位置关系，可分为锚固端头位于刀盘范围内以及锚固端头位于刀盘范围外，如图4 所示。由于锚杆中预应力的存在，此两种情况下盾构机滚刀的受力情况差别较大，因而此工况需要分类处理。值得注意的是，由工程经验可知，在直径为6 m的地铁隧道内，侵入锚杆层数大多数为1～2层，因此本文提出的工程指标是针对直径6 m的一般地铁隧道工程而言。

图4 盾构切削钢筋收集图Fig.4 Collection of rebar cut by shield machine

2.2.2钢筋累计长度

根据依托工程，当刀盘扭矩超过预设值，且掘进速度缓慢时，盾构机采用常压开仓方式处理。具体而言，盾构机人仓通道开启，操作人员通过人仓进入到土仓内，利用电焊等方式将刀盘上缠绕的钢筋清理干净，并通过人仓运出；同时，一并清除土仓内未排出的钢筋条与螺旋输送机开口处卡住的钢筋条（见图5）。此时，从盾构司机室的监测图像上发现，锚杆内的混凝土可以顺利随渣土运出，而皮带上并未出现刀盘切削下的钢筋。因此，我们可以认为通过刀盘切削下的钢筋并未从盾构机排出，即在相邻两次常压开仓处理之间，盾构机遭遇的地层钢筋全部集中在盾构机内部。因此，盾构机穿锚过程中，常压开仓后切削的地层锚杆钢筋总累计长度可以一定程度上概括盾构机遭遇的地层锚杆问题。

图5 盾构切削钢筋收集Fig.5 Collection of rebar cut by shield machine

2.2.3不同钢筋直径

实际工程中，桩锚支护的上下两层锚杆可能会采用不同直径的钢筋，因此钢筋直径也会对盾构机的掘进参数如扭矩等，造成一定程度的影响。因此，上下层钢筋的直径也被选作锚固地层的输入特征。

2.2.4盾构机操作参数

在正常盾构机掘进工程中，盾构机根据掘进表现及时调整操作参数，其主要包括盾构机刀盘转速、螺旋输送机转速以及刀盘推力。盾构机操作参数的选取在很大程度上影响着盾构机的掘进表现，因此，本文也将这三个主要操作参数作为输入特征。

2.3 输出量处理

盾构机穿锚过程中，锚杆内混凝土及钢筋与刀盘上滚刀相接触，使刀盘受到额外的作用力，其主要体现在盾构机扭矩迅速提高，推进速度减缓，即贯入度变小。因此，本文选取刀盘扭矩和贯入度作为输出量来评估盾构机掘进表现。

2.4 LightGBM模型建立

根据2.2节与2.3节的输入特征和输出量处理，本文依托水—洪区间穿锚工程，选取了9 个输入特征及2个输出量。输入特征分别为第一层锚杆端头是否位于刀盘范围内（如果位于刀盘范围内，该值取1，反之取0），第二层锚杆端头是否位于刀盘范围内（取值同上），自开仓处理后第一层锚杆钢筋累计长度，自开仓处理后第二层锚杆钢筋累计长度，开挖面第一层锚杆钢筋直径，开挖面第二层锚杆钢筋直径，刀盘转速，刀盘推力，螺旋输送机转速。输出量为盾构机掘进表现，分别为刀盘扭矩以及贯入度。

由工程概况，水～洪区间共有87 环管片侵入左线隧道。盾构机掘进过程中，刀盘每掘进30 cm 便记录一组数据，每组数据包括上述11 个相关参数，合计收集450 组数据。总数据集分为两部分数据集，分别用于贯入度的预测模型建立以及刀盘扭矩的预测模型建立。

本文将数据集以8：2 的比例随机分为训练集（360 组）和测试集（90 组），建模完成后对测试集进行预测性能评估。为使训练和测试速度加快，对输入数据进行归一化处理，创建LightGBM模型，初设random-state 为7，迭代次数为100，verbose_eval 为200，early_stopping_rounds 为200。参数设置如表1所示，num_leaves 为叶子节点数；learning_rate 为学习率，控制算法的迭代次数；min_sum_hessian_in_leaf为一个叶子上的最小样本数，分裂时出现某些点样本小于该值即停止分裂；bagging_freq 为bagging的频率；bagging_fraction 为选择数据和全部数据量的比率，范围为［0，1］；lambda_l1表示L1正则化。

表1 LightGBM训练参数表Tab.1 Training parameters in LightGBM model

参数设置完成后对模型进行训练，达到设定目标后保存模型，并输出预测结果。

2.5 LightGBM模型预测结果

建立预测模型之后需对模型的精确性进行评估，本文采取常见的定量指标，如决定系数R2，均方误差MSE，平均误差和标准误差值来评估模型的预测精度。决定系数、均方误差MSE、平均误差和标准误差值的计算如下：

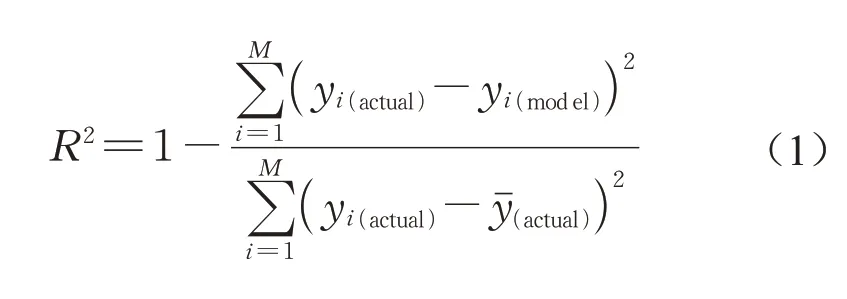
2.5.1贯入度预测结果

经过LightGBM 模型训练，本节对训练集和测试集的贯入度拟合结果分别进行了分析，分析图如图6～图9所示。

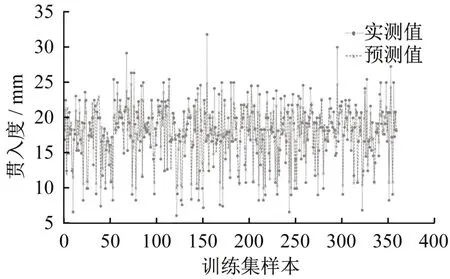
图6 LightGBM算法贯入度预测结果（训练集）Fig.6 PR result for the train phase of LightGBM model

图7 LightGBM算法贯入度预测结果（测试集）Fig.7 PR result for the test phase of LightGBM model

图8 LightGBM算法贯入度误差图（测试集）Fig.8 PR error for the test phase of LightGBM model

由预测结果图6～图9 可以看出，本文建立的LightGBM 模型对于贯入度的预测效果可勉强达到预期效果，测试集的决定系数为0.661 7，均方误差为5.983 1，平均误差为1.855 2，标准误差为2.312，接近83.3%的样本点误差在±2 mm 之间，因此可以对样本进行基本的预测，但仍可以进行优化。

图9 LightGBM算法贯入度误差分布直方图（测试集）Fig.9 Histogram of PR error for test phase of LightGBM model

2.5.2扭矩预测结果

本节对训练集和测试集的扭矩拟合结果分别进行了分析，分析图如图10～图13所示：

图10 LightGBM算法扭矩预测结果（训练集）Fig.10 Torque result for the train phase of LightGBM model

图11 LightGBM算法扭矩预测结果（测试集）Fig.11 Torque result for the test phase of LightGBM model

由预测图10～图13 可以看出，本文建立的LightGBM模型对于扭矩的预测效果差强人意，测试集的决定系数为0.947 6，均方误差为257.773 0，平均误差为13.653 1，标准误差为15.311，接近90%的样本点误差在±20 t·m 之间，可以对样本进行一定精度上的预测。

图12 LightGBM算法扭矩误差图（训练集）Fig.12 Torque error for test phase of LightGBM model

图13 LightGBM算法扭矩误差直方图（训练集）Fig.13 Histogram of torque error for test phase of LightGBM model

由贯入度和扭矩预测结果可以看出，LightGBM模型可勉强满足预测要求，但其中诸多参数的初始赋值不同，最终预测结果也存在较大差异，即可进行调整或优化以达到更好的预测精度［21］。但LightGBM模型中可调参数太多，手动调参将会浪费巨大时间及精力，仍难找到最优预测精度的模型初始赋值。因此为了该模型在本数据集上能够进行最优化的训练和识别预测，本文选取鲸鱼优化算法来进行优化。其中优化的是表1中的6个超参数，本文鲸鱼算法优化LightGBM的研究路线如图14所示。

图14 鲸鱼优化算法研究路线Fig.14 Research line by optimization of WOA

3 WOA-LightGBM模型构建

3.1 鲸鱼优化算法概述

鲸鱼优化算法是一种新颖的、受自然启发的元启发式优化算法，通过模拟座头鲸的狩猎行为，建立泡沫网搜索策略（见图15）。

图15 座头鲸围猎示意图Fig.15 Schematic of humpback whale hunt

座头鲸捕猎的行为模式分为两种，分别是缩小搜索范围和随机搜索，缩小搜索范围如下所示：

随机搜索是座头鲸寻找猎物的第二种方式，表达方式如下所示：

式中：t为迭代的次数；X为位置向量，代表座头鲸的位置；X*为每次迭代产生的最佳解，需要在每次迭代进行更新，A和C为系数，b为控制螺旋的范围，l是介于-1至1的随机数，A和C计算方法如下：

式中：a从2 至0依据迭代次数的倒数线性减小；r是介于0至1区间的随机数。

通过对两种搜寻方法等概率分配，以模拟座头鲸的真实行为模式，到达迭代最大次数时判定为搜寻结束。因此，针对LightGBM 模型初始赋值难以选择，预测结果不稳定的情况，本文选用WOA算法优化LightGBM 模型内的超参数，以提高模型的预测稳定性和精度。

3.2 WOA-LightGBM算法模型

LightGBM模型中可优化的超参数主要有6个，分别为num_leaves，learning_rate，min_sum_hessian_in_leaf，bagging_freq，bagging_fraction，lambda_l1。因此本文采用WOA 对上述参数进行寻优，模型建立过程如下：

（1）搜索代理（鲸鱼）数量设置为20，最大迭代次数为500。

（2）种群初始化。随机初始化所有鲸鱼的初始位置，保证在取值范围内。

（3）种群评估。以LightGBM算法得到的均方误差作为目标值，评估鲸鱼种群中每个鲸鱼的目标值，如有某个鲸鱼优于当前最优解，则将其设为最优解。

（4）设置和迭代次数相关的算法参数。

（5）对每个鲸鱼的每一维度进行位置更新。

（6）重复执行步骤3～步骤5。

3.3 WOA-LightGBM模型验证

因贯入度的预测模型和扭矩的预测模型不同，因此需要对两模型进行单独优化。对于贯入度预测模型而言，经过多次迭代过后，最终优化得到的WOA-LightGBM模型参数如表2所示：

表2 WOA-LightGBM贯入度模型参数表Tab.2 Training parameter in LightGBM model for predicting torque

取贯入度平均误差作为适应度指标，随迭代而优化的适应度曲线如图16所示：

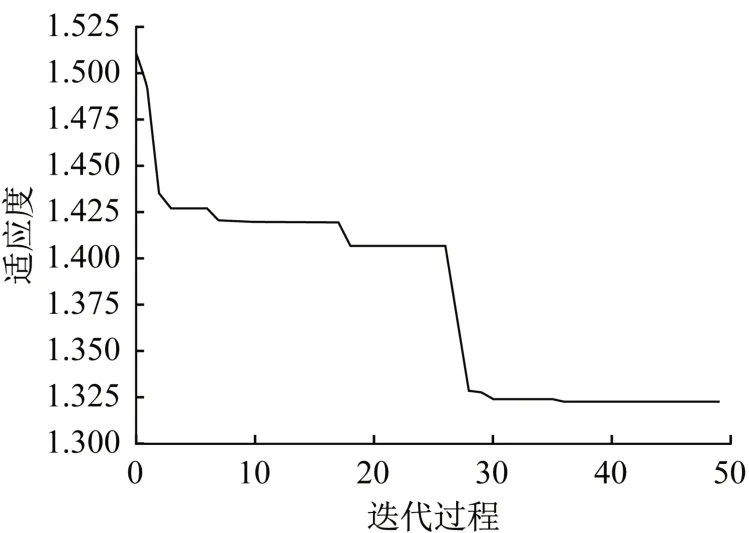
图16 WOA优化下贯入度平均误差Fig.16 Mean error of PR based on WOA optimization

由图16 所示，经过鲸鱼算法优化后的WOALightGBM模型，平均误差明显下降，最终稳定在1.320 7，比LightGBM模型时优化了28.6%，同时经计算此时均方误差MSE为3.009 4，决定系数为0.773 3。

对于扭矩预测模型而言，经过多次迭代过后，最终优化得到的WOA-LightGBM参数如表3所示：

表3 WOA-LightGBM扭矩模型参数Tab.3 Training parameter in WOA-LightGBM model for predicting torque

同上，取扭矩平均误差作为适应度指标，随迭代而变化的适应度曲线如图17所示：

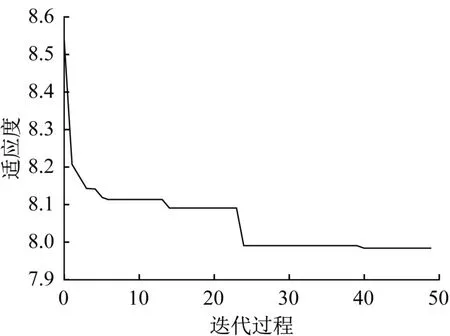
图17 WOA优化下扭矩平均误差图Fig.17 Mean error of torque based on WOA optimization

由图17 所示，经过鲸鱼算法优化后的WOALightGBM 模型，预测扭矩平均误差下降明显，最终稳定在7.98，比LightGBM 模型优化了41.3%。经计算，此时均方误差MSE 为201.52，决定系数为0.958 3，大大提高了LightGBM的预测准确性，满足工程实际需要。

3.4 WOA-LightGBM模型预测精度

为探讨本文提出的WOA-LightGBM 模型的精确性，本文同时构建了工程问题中频繁使用的ELM（Extreme Learning Machine）与BP 神经网络模型作为横向对比［22-23］。两新建模型均将数据集打乱后归一化，同时取训练集与测试集比例为8：2。

BP神经网络设置如下：设定网络隐层和输出层激励函数分别为tansig和logsig函数，网络训练函数为traingdx，网络性能函数为mse，隐层神经元数初设为8。设定网络参数如下：网络迭代次数epochs为1 000 次，期望误差goal 为0.000 1，学习速率lr 为0.01。ELM 神经网络设置如下：传递函数选择Sigmoidal function，30 层隐层神经元。此两种神经网络模型各进行20次训练，取试验平均值作为最终结果，试验结果见表4～表5。

表4 三种模型预测精度（贯入度指标）Tab.4 Prediction performance of three models for predicting PR

表5 三种模型预测精度（扭矩指标）Tab.5 Prediction performance of three models for predicting torque

值得注意的是，在表4和表5中，本文选取了给定误差域占比指标分析预测精度。由图9和图13可以发现，误差相对集中在零附近。因此，本文对贯入度模型和扭矩模型分别设定了可接受误差区间，并借此辅助判断预测精度。对比工程中常采用的两种神经网络模型，本文优化的WOA-LightGBM模型可以在复杂盾构穿锚问题中更好地预测盾构机掘进性能，其均方误差降低了约25%，平均误差降低了约27%，给定误差域占比也有所提高，在预测精度上比神经网络算法更具有优势。由于样本数量并非过于庞大，WOA-LightGBM模型运算速度稍快，但差别不是特别显著。

4 结论

本文在分析锚固地层工程特性的基础上，建立了一套盾构机穿锚预测模型，并依托武汉地铁工程的掘进数据集进行LightGBM 模型的建立，并基于鲸鱼优化算法对LightGBM 的超参数进行了寻优，得到了LightGBM 模型内超参数的最优组合。经分析该WOA-LightGBM 模型预测精度高，运行速度快，可满足实际工程需要。具体结论如下：

（1）本文针对盾构机穿越锚固区的问题，分析选取了盾构机穿锚预测模型所需的输入特征，共包括6个可指代锚固地层特征的相关工程指标及3个盾构机操作参数，选取了2 个可体现盾构机掘进性能的输出量，经后续人工智能模型验证，本文建立的盾构机穿锚预测模型可成功预测盾构机掘进性能。

（2）对于实时收集的盾构穿锚数据集，本文选取的LightGBM模型一定程度上可预测掘进参数的变化情况，贯入度平均误差维持在2 mm 附近，刀盘扭矩平均误差在13 t·m 附近，证明了LightGBM 模型的有效性及适用性，但缺点是模型初始参数过多，难以准确合理赋值以达到最佳预测效果。

（3）本文提出的WOA-LightGBM模型采用鲸鱼优化算法解决了LightGBM模型初始参数赋值的难题，成功得到了LightGBM初始参数的最优组合解。经实际检验，对比传统BP神经网络和ELM模型，优化后的WOA-LightGBM 模型可将均方误差降低约25%，平均误差降低约27%，给定误差域占比也有所提高，精确度更高，适用性更高。

作者贡献声明：

叶飞：提出论文框架，指导数据分析，论文修改；

冯浩岚：完成数据分析及论文撰写；

梁兴：指导数据分析，论文修改；

刘畅：提供建模指导，论文修改；

梁晓明：提供现场图片；

张稳军：论文修改。