基于AR模型的直升机桨叶模态的识别方法有效性研究

程智恒

（南京航空航天大学航空学院，江苏 南京 210016）

直升机的振动特性对机体的安全影响十分大，其中桨叶上的振动最为关键和复杂，准确识别出桨叶的振动模态不仅影响着对振动的控制，也对机体的安全具有重要意义。

模态分析分为有限元分析法、试验模态分析法和运行模态分析法[1]。有限元法由于条件的限制，无法达到较高精度；试验模态分析法则由于试验和真实环境的差异以及施加激励的难度，限制了其适用范围；运行模态分析则只需要采集响应信号即可识别模态参数。

从时域、频域、时频域进行运行模态分析也存在不同特点[2]。时域法（如Ibrahim时域法、最小二乘复指数法、随机子空间法等）不用将测得的响应和激励信号变换到频域中进行参数识别，但难以测得载荷，且噪声易引起虚假模态和模型难定阶。频域法（如峰值拾取法、频域分解法、最小二乘复频域法等）技术发展较为成熟，对噪声的处理也较好，模态分布直观，但只适用于低阻尼结构并且对阻尼识别效果较差。时频法（如小波变换、短时傅里叶变换等）不具有时域法的噪声、定阶问题和频域法只适用于低阻尼结构、阻尼识别效果差的问题，却受限于基于时域和频域的信息的繁杂计算过程。

何绪飞等[3]利用小波域的AR模型实现了对直升机机体的模态参数识别。胡嘉苗等[4]利用Periodic PO-MOESS算法成功识别风塔机受到周期激励的结构模态。杭晓晨等[5]利用AR模型谱估计对频域分解法进行了改进，验证了这种方法对识别固定翼机翼振动模态的有效性，其试验表明，这种改进提高了阻尼识别精度和模态分布的可视性。

鉴于频域法的直观和计算的简单，并且噪声易处理，本文采取基于AR模型的频域分解法对直升机桨叶模态应用的有效性进行了分析，验证了这种方法能够有效识别旋转桨叶固有频率。

1 频域分解法的基本理论

频域分解法是在峰值拾取法的基础上发展起来的一种频域模态参数的识别办法[6]。其基本原理是系统的频率响应函数峰值可以代表自身的震荡频率，自身固有频率可以作为特征频率的良好估计结果。频域分解法是将结构响应的功率谱密度函数在峰值处进行奇异值分解，得到对应的结构多模态的单自由度系统功率谱密度函数。输出响应的功率谱密度Gyy（m×m的矩阵）可由下式求得[7]：

式（1）中：H（jω）是结构的频响函数矩阵；Gxx（jω）为激励的功率谱密度矩阵，为r×r阶的矩阵，结构外部激励为u（t），结构响应为y（t）。

利用频域分解法识别固有频率，横纵坐标分别为频率和输出响应的功率谱奇异值。利用奇异值分解，可以使奇异值曲线在分解过程中从大到小重新排列，奇异值曲线中占主导地位的是第一条奇异值分解曲线[8]。第一条奇异值曲线功率谱图中峰值对应的频率即结构固有频率，峰值处奇异值对应的奇异值向量为结构振型。

2 AR模型求功率谱

AR模型是一种线性预测[7]，原理是由已知的N个数据，根据模型来推出N点前后的数据。不同于差值法由两点或者少数几点去推导多点，AR模型由N点去进行递推，比差值增加了有效数据，因此预测效果比插值方法好。

为解决经典功率谱估计方法的平均周期图法的方差性较差、分辨率较低的问题，并且相对于自相关算法，Burg算法计算简单且分辨率较高，因此本文采取基于AR模型的Burg法进行谱估计，并进行试验验证其谱估计效果。

AR参数模型如下：

式（2）中：u（n）为白噪声信号。

方差σ2的白噪声序列作为输入信号，其中AR模型阶数p则是未知的，需要通过定阶准则来对模型定阶。本文采用FPE准则来完成定阶。最终预报误差（FPE）准则，其判断依据就是最终预报误差最小情况来确定AR模型阶数p。最终预报误差可由下式表示：

对AR模型表达式求z变换，得到系统函数：

根据功率谱和傅里叶变换的关系因此可求功率谱密度为：

因此，整个问题转化为估计模型的参数ak进而求出信号的功率谱。

Burg算法是首先令前后项预测误差功率之和为最小估计出反射系数，再迭代计算估计出AR模型参数，反射系数计算如下：

其中：

3 算例研究

3.1 模拟信号仿真

功率谱估计主要研究信号在频域中的各种特征，目的是根据有限数据在频域内提取被淹没在噪声中的有用信号[9]。本节选取2个频率，分别为50 Hz和200 Hz的正弦信号的叠加信号，再叠加高斯白噪声作为仿真信号，采样周期为0.001 s，采样点数量为1 000。采用频域分解法常用谱估计方法中的周期图法、Welch法和基于AR模型的自相关法与基于AR模型的Burg算法进行对比，分析AR功率谱估计效果及影响AR谱估计的因素[8]，如图1—图5所示。

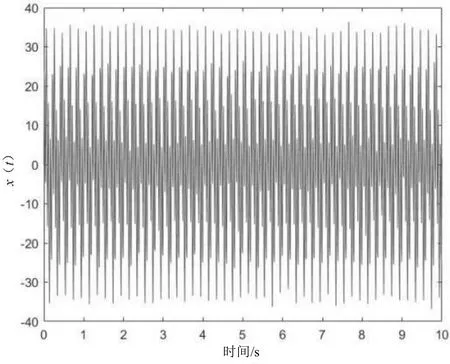
图1 仿真信号

图2 基于周期图法的功率谱估计

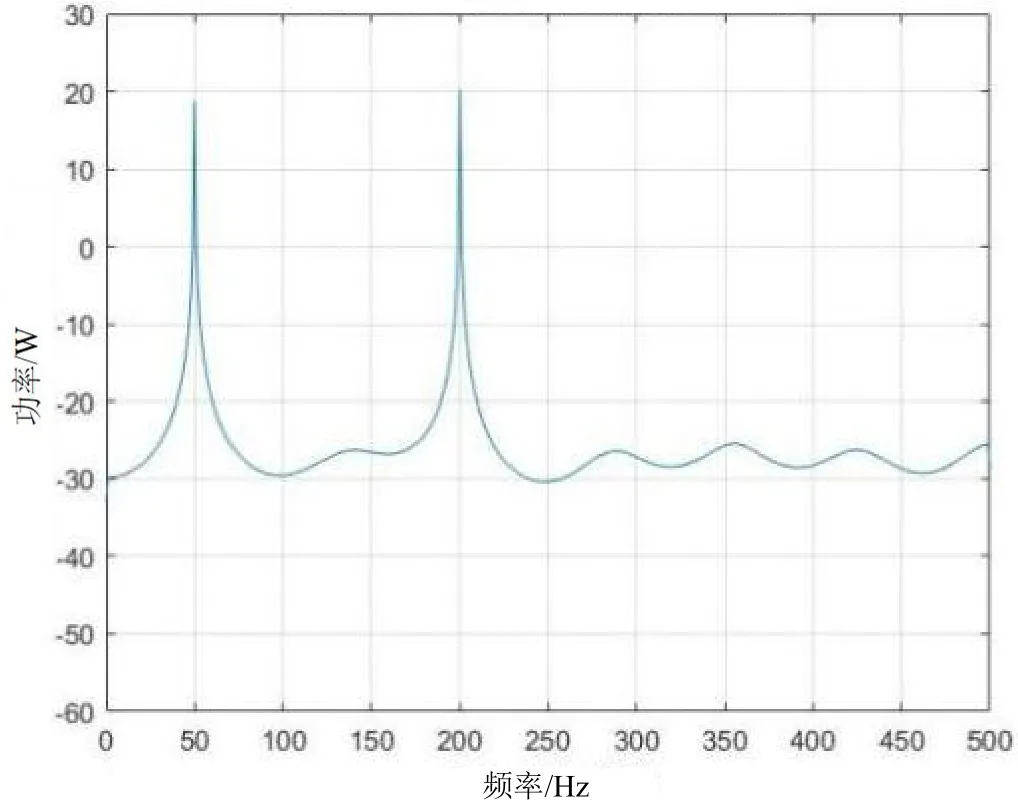
图5 基于Burg法的功率谱估计

图3 基于自相关函数的功率谱估计

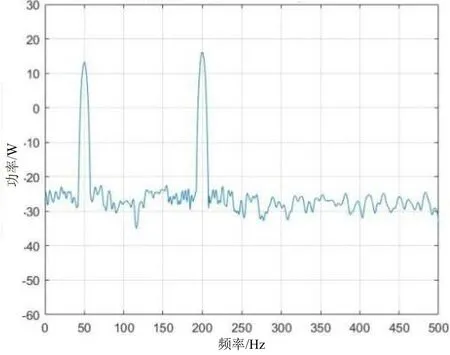
图4 基于Welch法的功率谱估计

仿真结果显示，周期图法估计结果与自相关函数法都有高分辨率的峰值，但是功率谱曲线毛刺较多，而Welch法对曲线毛刺突出有所压制，但却降低了峰值的分辨率，使得峰值不够尖锐突出。基于Burg法的AR模型的功率谱不仅仅在峰指处尖锐分辨率高，曲线也光滑没有毛刺干扰，显示效果理想。

但是在仿真过程中发现，不同阶次的AR模型谱估计结果差异较大，下面对不同阶次的模型谱估计进行仿真并对结果进行分析。

各阶AR模型功率谱效果图如图6所示。从图6中可以得到，当模型阶数从低逐渐升高时，曲线的显示效果也从平滑不明显到峰值突出曲线平滑，再变成峰值突出曲线出现毛刺，直至最后毛刺明显产生虚假峰。因此在AR模型谱估计中，需要选择合适的模型阶数，过低会导致峰值不明显，过高则会导致图谱曲线出现毛刺和假峰。结果表明模型定阶的必要性，合适的模型阶数能够提高功率谱图峰值分辨率，得到清晰的谱峰和较小的估计方差。

图6 各阶AR模型功率谱效果图

3.2 多自由度的密集模态识别仿真

下面将基于AR模型的频域分解法对多自由度结构的密集模态进行识别和分析，确保应用时不会产生模态遗漏。

自由度分别为2、4、6、8的结构的功率谱图如图7—图10所示，并且根据识别出的结构固有频率与结构实际固有频率的比较，得到估计的误差结果，如表1所示。其中仿真输入信号如下：

式（4）中：n为结构自由度数；fk为输入频率；m为采样点数。

从图7—图10中可得出，多自由的结构的AR功率谱图的峰值明显易区分。表1中的数据显示，固有频率的估计结果与实际固有频率的数值的误差最大不超过2%，识别结果显示理想，因此AR模型的谱估计对密集模态也适用。

图7 2自由度系统功率谱图

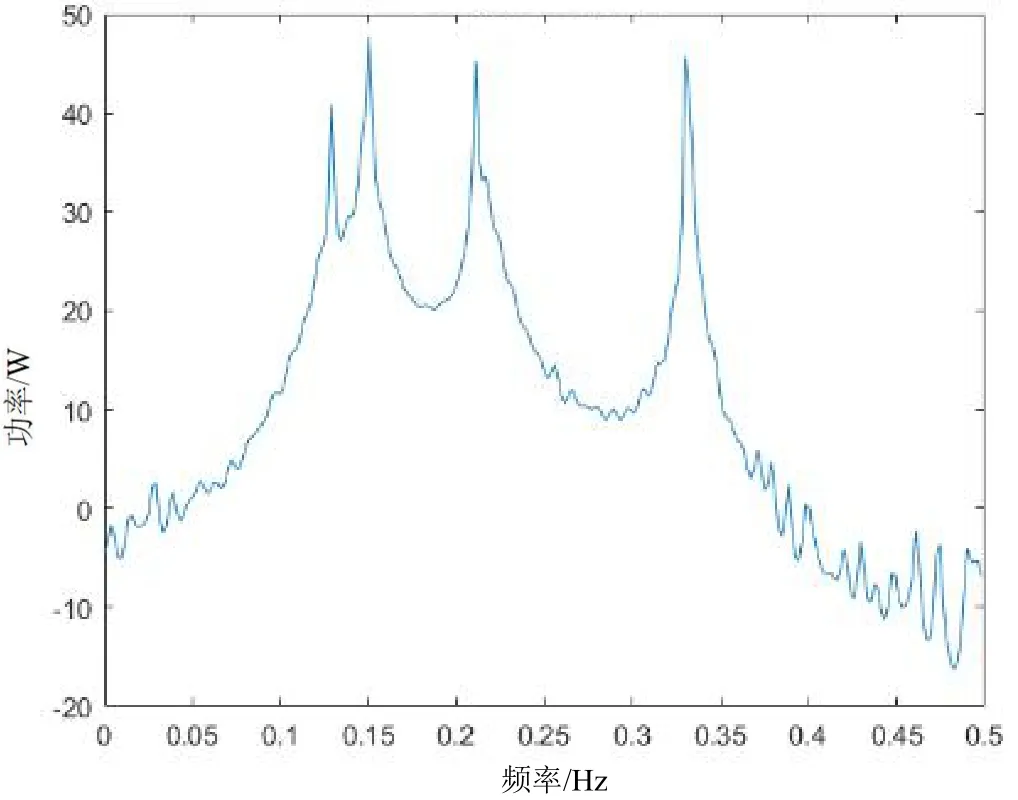
图8 4自由度系统功率谱图

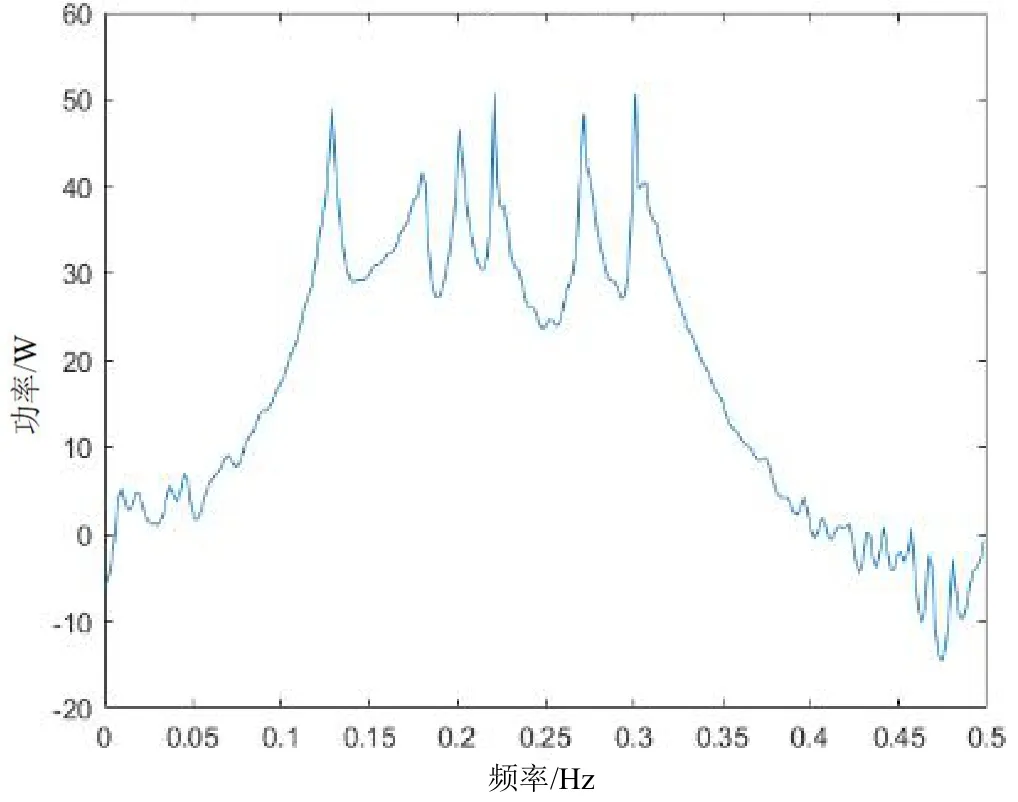
图9 6自由度系统功率谱图

图10 8自由度系统功率谱图

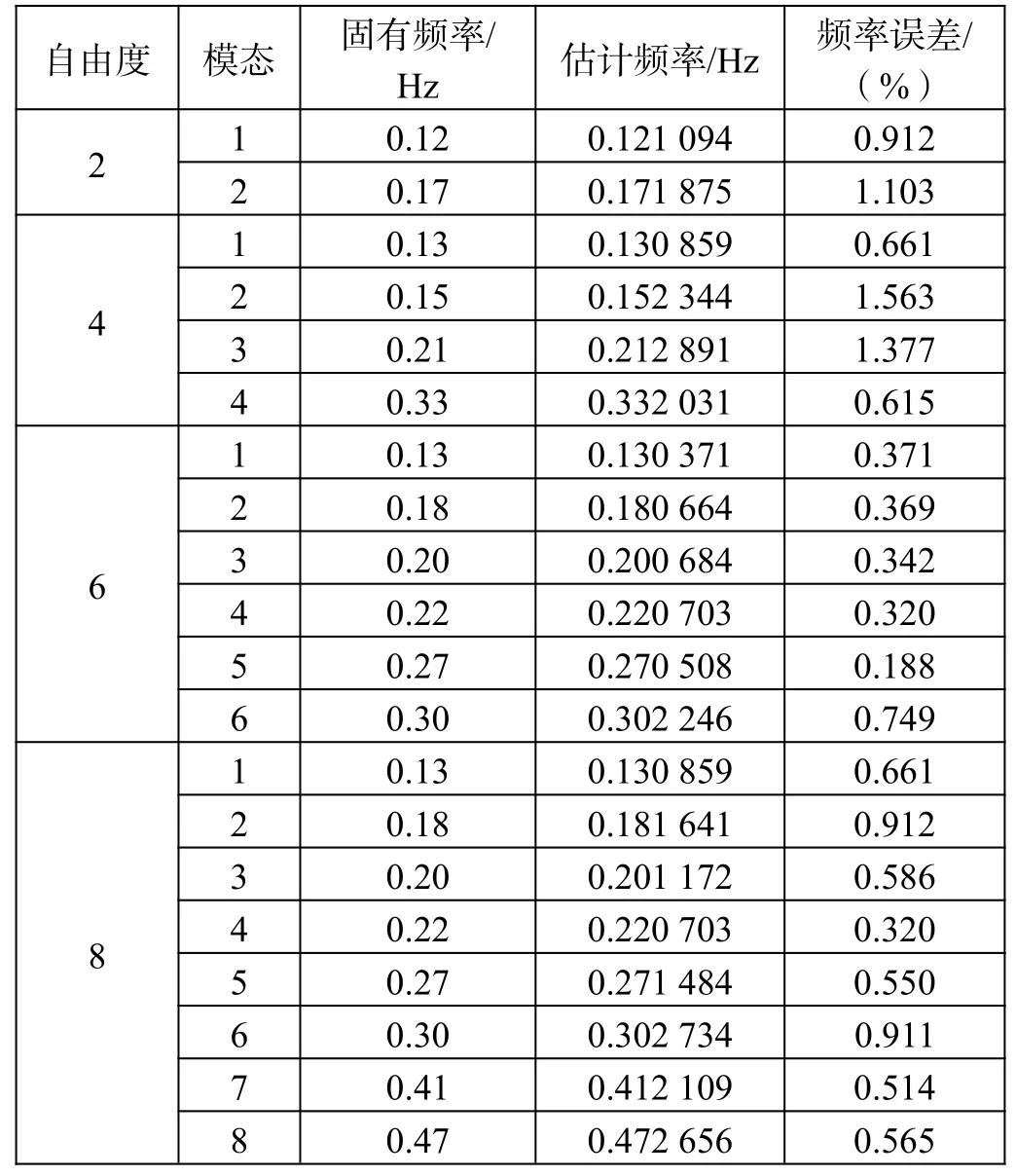
表1 多自由度结构固有频率识别

3.3 旋转桨叶运行模态参数识别

前面研究了在仿真信号输入的情况下的识别效果，并得到了理想的结果。下面将根据基于AR模型谱估计的频域分解法，通过MATLAB进行模态参数识别的编程，对桨叶真实工作情况下的振动数据进行处理和识别，证明对桨叶模态识别的有效性。

为了通过有限元求得理想数值，且没有变距的运动桨叶与旋转梁的工作情况相似，下面试验将对搭建的旋翼试验台进行旋转梁试验，模拟旋转桨叶的运动，对桨叶固有频率进行识别，与有限元方法得到的理论结果进行对比，分析与理论数值的误差。

其中梁的测点、旋转梁试验台分别如图11和图12所示，计算结果如表2所示。

图11 梁的测点贴片

图12 旋转梁试验台

表2 梁模型固有模态频率

从表2中的数据可知，将经典频域分解法和基于AR模型谱估计的频域分解法得到的固有频率与有限元法计算得到的理论结果进行比较，2种方法的最大误差均在可以接受的范围之内，即经典频域分解法与基于AR模型谱估计的频域分解法用于刚性旋转桨叶模态参数的识别中是可行的，但基于AR模型谱估计的频域分解法更接近理论值，误差更小。

4 结论

基于AR模型谱估计的结果直观、谱峰明显易拾取且分辨率较高的优点，本文对基于AR模型谱估计的频域分解法进行了密集模态识别验证，分析了影响其模态分析效果的因素，并对其应用在直升机桨叶上的有效性进行旋转梁试验验证。结果表明基于AR模型谱估计的频域分解法相较于经典频域分解法，其功率谱图的峰值更突出易拾取，并能够对密集模态精确识别，且模态识别精度更高，虽然谱估计效果在很大程度上取决于模型的阶数取值，利用定阶准则就能够解决这一问题，结果表明此方法适用于直升机桨叶的模态识别。