极端海况下岛礁岸坡渗流及动力稳定性分析

荣 泽，年廷凯，张 浩，郑德凤，付崔伟

(1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；2.辽宁师范大学 自然地理与空间信息科学重点实验室，大连 116029；3.中铁第一勘察设计院集团有限公司，陕西 西安 710043)

岛礁岸坡是一种特殊的海岸形式，通常由陡峭的礁前斜坡和相对平坦的礁坪组成[1]。当遭遇台风海况时会出现巨浪作用而发生渗流，在坡体内产生不利的孔隙水压力或渗透压力，会引发岸坡失稳，造成吹填体滑塌、上部基础设施破坏等链式灾害问题；而地震荷载会导致坡体内产生动应力和超孔压，同样会危及坡体稳定性甚至诱发滑坡。因此开展巨浪和强震等极端海况下岛礁岸坡的稳定性分析十分重要。

岛礁岸坡稳定性分析，整体上与陆上各类边坡稳定性分析方法类似，但由于岛礁地形和水下地质环境的复杂性，导致海上工程地质勘测工作有些难度，要获得准确的地层分布和土性参数难度更大，特别是要考虑岛礁岸坡的渗流和动力特性，使得其稳定性分析变得更加困难，故起步较晚。郭见扬[2]对珊瑚岛礁的地层、岩石成因和区域稳定性等进行了定性化描述；詹文欢等[3]通过对珊瑚岛礁群的调查研究，总结归纳了场地内的活动断裂和多发性灾害地质问题；崔永圣等[4-5]基于各类先进的物探方法，进一步调查了珊瑚岛礁的特殊岩土工程地质特征，为后续岛礁岸坡的稳定性定量分析提供了基础数据。胡进军等[6]针对南海岛礁场地的吹填土开展了物理力学性质方面的试验研究；刘清君等[7]通过模型试验研究了规则波作用下岛礁地形上波浪破碎点相对距离与Irribarren数、礁坪相对水深以及前坡坡度的密切关系，推导了经验公式；并进一步开展了岛礁地形在抛石护岸条件下稳定性的试验研究，发现抛石护岸边坡的稳定性与岸坡宽度有关[1]；叶剑红等[8]采用大型物理模型水槽试验，研究了波浪荷载作用下南海岛礁护岸防波堤的稳定性，探究了极端波浪条件下防波堤的位移、越浪量以及地基内的孔隙压力是否存在累计上升等现象。对于地震作用下岛礁地形的动力响应方面，胡进军等[9]探究了不同脉冲型地震动情况下珊瑚岛礁场地的放大倍数，对珊瑚岛礁场地地震反应分析进行了初步探索；陈国兴等[10]进一步研究了珊瑚岛礁场地的地震反应特征，填补了南海岛礁场地地震效应研究的空白，但未考虑海水-岛礁体相互作用；张巍等[11]则建立了海水-岛礁-地震耦合的岛礁数值模型，考虑流固耦合作用，深入分析了岛礁场地的地震反应规律。

综上所述，前人对岛礁岸坡在波浪、地震荷载作用下的动态反应进行了不少研究，且开展了实际岛礁岸坡的物理模型试验，但采用数值模拟手段进行极端海况下岛礁岸坡的渗流和动力响应方面的研究还相对较少，也缺乏针对具体案例的深入稳定性分析。

基于此，本文以南海吹填岛礁典型护岸边坡工程为例，采用数值分析方法与极限平衡法相结合的研究手段，对极端海浪条件下岛礁岸坡进行有限元渗流稳定性分析，并开展地震荷载作用下的动力稳定性分析，以期丰富岛礁岸坡的稳定性分析方法，为同类工程建设和安全运营提供技术参考。

1 渗流及动力稳定性分析方法

1.1 渗流有限元控制方程

基于达西定律和质量守恒方程，各向异性土中非稳定渗流的微分方程可表示为:

(1)

式中:ρ为水的密度;β为水压缩模量;α为土压缩模量;n为土体孔隙率[12]。稳定渗流的微分方程即等式(1)右侧为零。

采用Seep/W有限元分析模块进行求解，获得岛礁岸坡的渗流场、变形场和应力场以及动态反馈。

1.2 动力有限元控制方程

对于地震荷载作用下的岛礁岸坡动应力场求解，其动态响应的有限元控制方程为式(2)，其中荷载{F}由体荷载、边界荷载、集中荷载和地震荷载共同组成，见式(3)。由牛顿第二定律可知，地震动力荷载为节点加速度向量与总体质量矩阵之积，见式(4)。通过平方根法求解动力有限元方程，可得到每一单元高斯点的应力应变结果[13]。

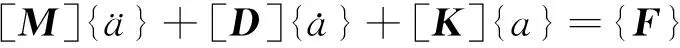
(2)

{F}={Fg}+{Fb}+{Fs}+{Fn}

(3)

(4)

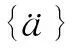
1.3 基于有限元法的边坡极限平衡稳定性分析

极限平衡法通过静力平衡原理分析岸坡的受力特点，在滑移体范围内将土体划分成若干个竖向的条块，针对每个小条块建立力或力矩的平衡方程，经由抗滑力与下滑力之间的相对大小关系来评价其稳定性。在运用极限平衡法进行稳定性分析时，边坡破坏的滑移面遵循摩尔-库仑强度准则，其表达式为：

τf=αtanφ+c

(5)

式中:τf为土体的抗剪强度;σ为剪切面上的法向应力；φ为土的内摩擦角;c为土的黏聚力。当剪应力τ≥τf时，滑移面被“剪坏”，即当某一平面上的剪应力和法向应力满足式(5)时，该平面处于极限平衡状态。

对于渗流及动力问题的分析，有限元极限平衡法很好地结合了极限平衡法和有限元应力分析法的特点[14]，通过弹塑性有限元分析，精准把握边坡整体应力场的影响，进而确定当前应力场中最危险滑动面的位置及其对应的安全系数。滑动面安全系数Fs为滑动面上土体的抗剪强度和实际剪应力的比值：

(6)

式中:l为滑移面滑弧长度；c、φ分别为土体的黏聚力和内摩擦角；本文有限元极限平衡法是通过应力变形分析实现的[15]。

2 典型岛礁岸坡渗流稳定性

2.1 典型岛礁岸坡工程地质条件

岛礁护岸防波堤是保证礁坪上吹填体稳定的工程构筑物，以我国南海某一吹填体岛礁的典型护岸边坡工程地质剖面为例，南海典型吹填体岸坡剖面各部分具体尺寸参照图1(a)，各分区材料的物理力学参数见表1。针对极端海况下吹填岛礁岸坡无防波堤(图1(b))和有防波堤(图1(c))的两种岸坡形式，分别开展渗流和动力稳定性分析。其中，岛礁护岸防波堤由胸墙及S型护坡两大部分组成，由混凝土浇筑而成[8]。岛礁护岸防波堤的地基材料根据南海海域南沙群岛珊瑚礁浅地层的地质特征划分为上下两层：上层为钙质砂，下层为礁灰岩(由砂与碎石的混合物等效)。由于现场岛礁礁坪坡面地形变化显著，因此在建立模型时采用统一坡度近似表示[8]。

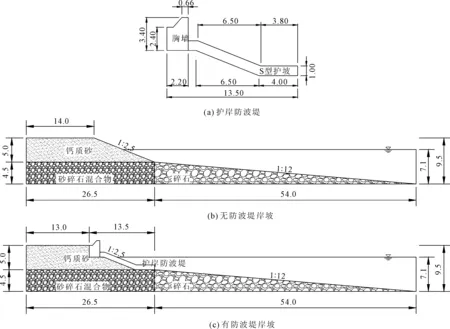
图1 南海典型岛礁护岸边坡剖面图[8](单位：m)

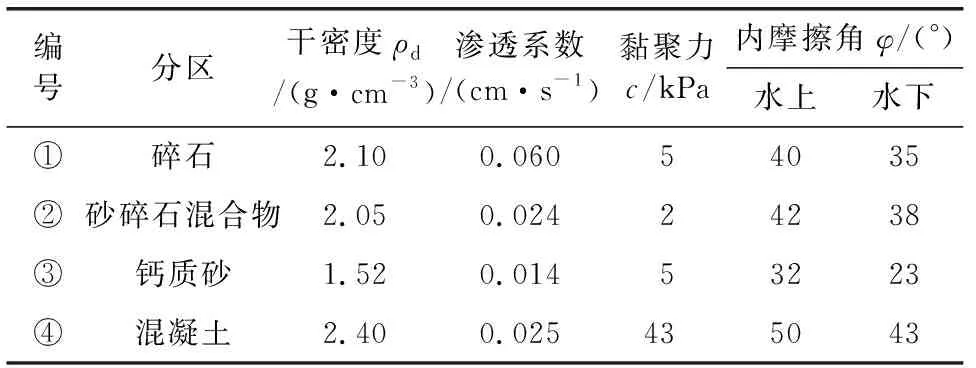
表1 岛礁护岸边坡各分区材料参数取值

根据边坡地质原型以及工程地质条件，有护岸防波堤的模型分为四部分：①碎石，②砂碎石混合物，③钙质砂，④预制混凝土；无护岸防波堤的模型只有三部分，不包含④预制混凝土。渗流计算应当考虑吹填体有无护岸防波堤保护，因此渗流分析按图1(b)和图1(c)两种不同分区情况考虑(吹填体坡度均为1∶2.5)，网格划分无护岸防波堤的剖面共计1 534个节点，1 370个单元(见图2(a))，有护岸防波堤的剖面共计1 532个节点，1 364个单元(见图2(b))，均采用混合单元(三角形&四边形)模式。

图2 南海典型岛礁护岸边坡有限元网格划分图

渗流建模应当考虑海水涨退潮，尤其是潮位可能出现的极端情况，因此荷载程度分类如下：

(1) 正常海平面位置，即如图1所示7.1 m处。

(2) 极端海平面位置，与钙质砂土层上位面相平，即9.5 m。

2.2 考虑退潮过程的岛礁岸坡渗流稳定性分析

实际沿海环境，海水总处于涨潮与退潮的动态变化，本节考虑水位从初始极端海平面9.5 m降落至正常海平面7.1 m，这一动态过程对岛礁岸坡稳定性的影响。假定整个退潮过程在12 h内完成，取水位下降结束瞬间进行对比，滑移体及总水头如图3所示。按动态水位模拟，无防波堤的情况下最小安全系数由4.506降至2.792(见图3(a))，有防波堤的情况下由4.959降至3.287(见图3(b))。瞬态水位降落，引发顺坡渗流，使得斜坡稳定性有所降低，而对于有防波堤的岸坡，其安全系数均高于无防波堤的岸坡，这说明了护岸防波堤保证了在大潮位变化情形下岛礁岸坡的稳定性。

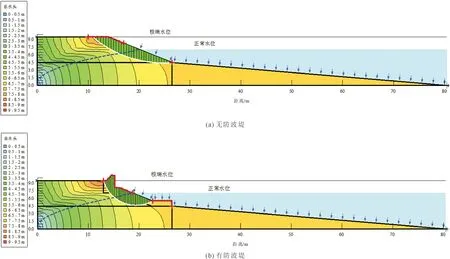
图3 水位骤降时岛礁岸坡临界滑移面位置及孔压分布

2.3 极端波浪荷载下岛礁岸坡稳定性分析

风暴潮产生的波浪荷载是南海岛礁岸坡所受到的最频繁动荷载，砂土质边坡失稳更是与波浪作用密切相关。波浪荷载导致岛礁岸坡失稳的主要原因为：(1)土体的剪应力由于波浪作用下发生突变；(2)土体的抗剪强度由于有效应力下降而减小；(3)土体内部孔压急剧变化。随着剪应力突增和土体抗剪强度下降，滑坡更易失稳[16]。本节将简谐波浪荷载转化为等效均布荷载，利用拟静力方法，探究波浪荷载对岛礁岸坡稳定性的影响。

岛礁岸坡属于浅水区，应用艾里波理论定义等效海底波压力，波浪对海底波压力的表达式为[17]：

(7)

式中:γw为水重度，取10 kN/m3;H为波高;h为水深。根据前人的研究可得，岛礁岸坡防波堤的胸墙受到设防极端风浪冲击时，最大冲击力能够达到50 kPa，护坡所受冲击力峰值在10 kPa～15 kPa之间[8]。同时，水深越深，波浪作用越弱。对波浪荷载按最不利因素进行拟静力等效，即认为波浪力均布于坡面，在宏观上对斜坡表现为垂直坡面向外的拉力，如图4所示。

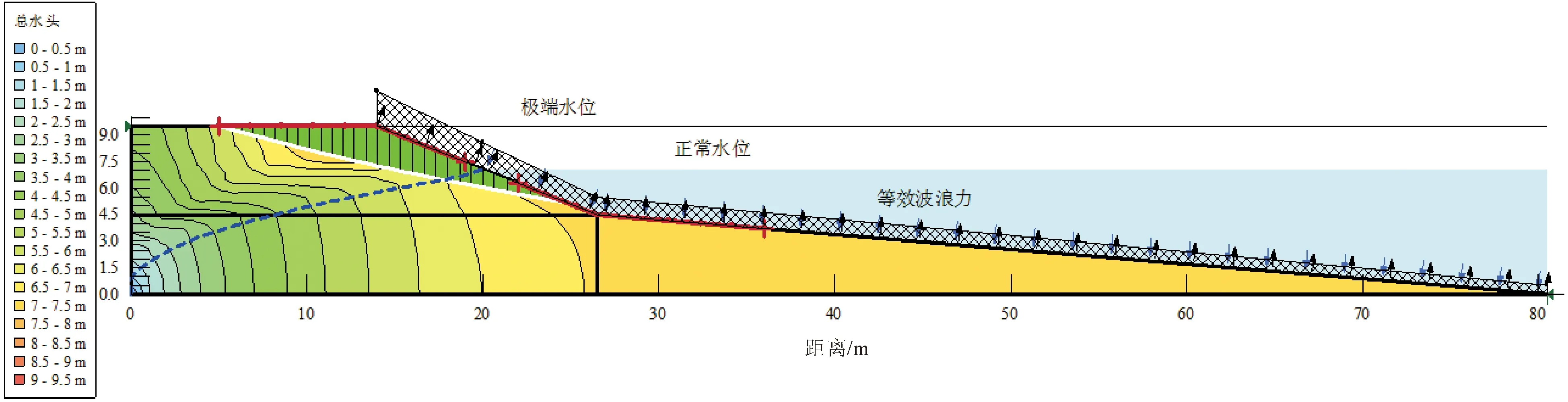
图4 波浪作用下岛礁岸坡临界滑移面及孔压分布

通过计算可得，无防波堤时在极端水位和退潮至正常水位条件下受波浪作用的岸坡安全系数分别为0.917和0.431，此时岸坡处于失稳状态；相对地，有防波堤时在极端水位下最小安全系数为1.784，在退潮后正常水位下为1.654，岸坡处于稳定状态。

对比3.2节考虑退潮过程的稳定性分析，可知当波浪力对岸坡作用时，有防波堤和无防波堤的岸坡最小安全系数分别降低了约50%、85%；相对地，防波堤使得极端水位和退潮至正常水位条件下的岸坡最小安全系数相比受波浪作用的无护坡情形分别提高了约49%、74%。以上结果表明风浪冲击进一步降低了岸坡的稳定性，对岸坡安全稳定产生更大威胁，同时护岸防波堤在应对风浪冲击时，弱化了波浪冲击影响，显著提高了岸坡的安全系数，保证了岛礁岸坡的稳定性和耐久性。

3 岛礁岸坡动力稳定性

3.1 岛礁岸坡地震动力响应分析

地震产生的加速度增加了海底斜坡的下滑力，同时土体内部孔隙水压力增大，形成流体超压，从而降低斜坡土体的抗剪强度，致使海底斜坡发生失稳破坏[18]。南海吹填岛礁场地地震频发，因此进行岛礁岸坡在地震荷载作用下的动力响应分析具有重要意义[19]。本节探究岛礁岸坡在20 s实际水平地震加速度作用下(如图5所示唐山地震区地震波数据)作用下的动力响应，以0.01 s为时间步长，岸坡坡顶前端顶点为位移响应点，观察岸坡稳定性及变形情况。

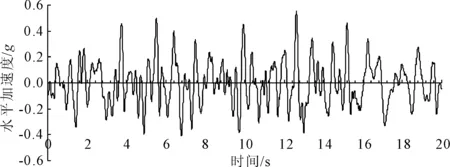
图5 地震时程曲线(20 s)

由地震时程曲线可知，某些振动时刻(加速度为负值，积分位移逆滑移方向增加)可以抑制滑移体滑动，某些振动时刻(加速度为正值，积分位移顺滑移方向增加)则促使滑移体滑动。因此，地震动力作用在某一时刻安全系数可能降低，也可能升高。对超出屈服加速度的加速度量进行积分运算，可得出地震动力作用下的岸坡累积变形[20]，位移响应特征点结果如图6所示。无护岸防波堤时，该砂质边坡无法保持稳定，变形不断积累，最终剪切破坏(见图6(a))；有护岸防波堤时，边坡累积变形小于0.1 m(见图6(b))，相比前者形变较小，稳定性在一定程度上得到保证。

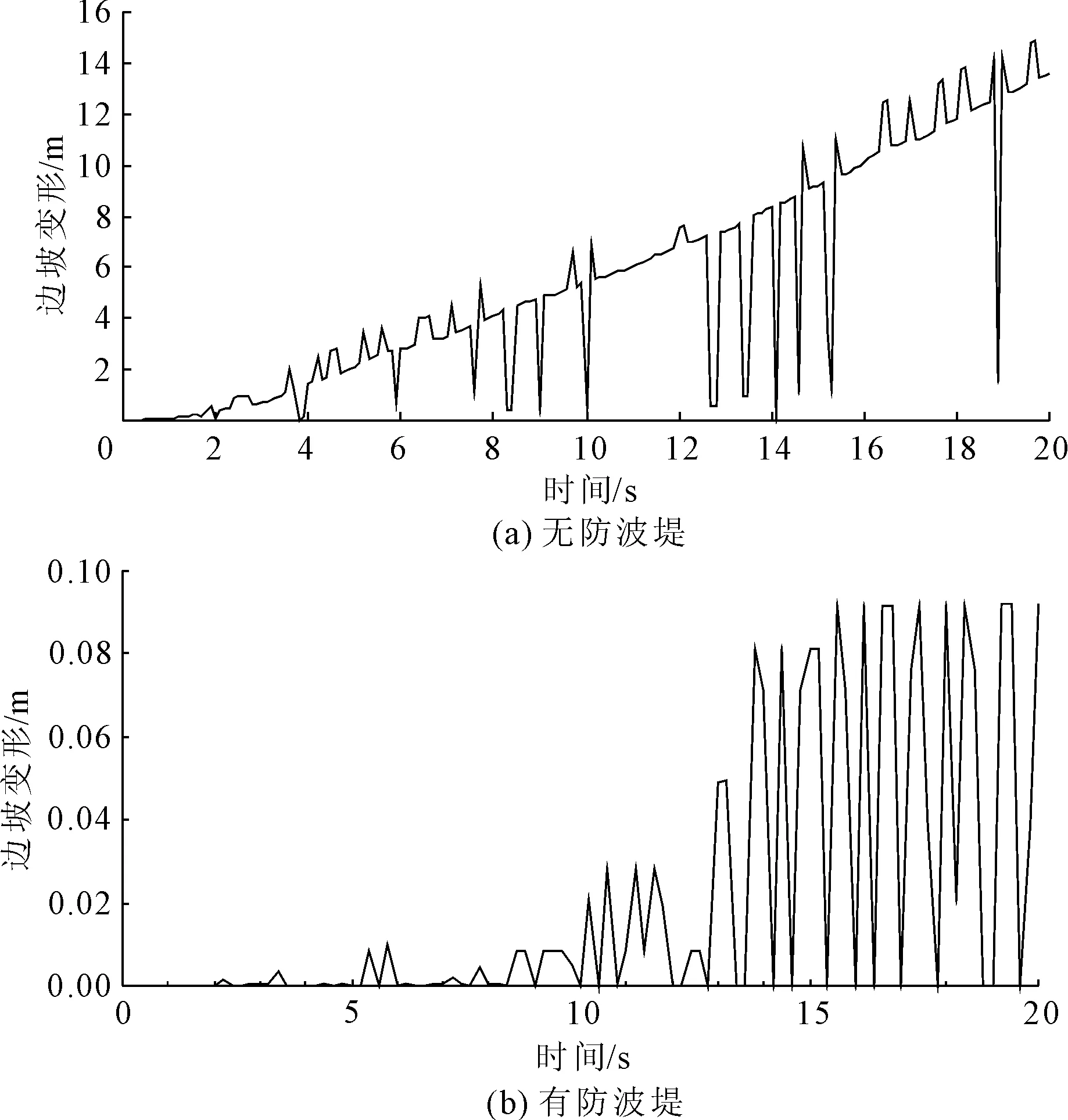
图6 岸坡累积变形示意图

3.2 岛礁岸坡拟静力地震稳定性分析

拟静力法也称为等效荷载法：加速度可以产生惯性力，引发地震动力效应，这些力以水平力Fh和竖向力Fv的形式作用在每一个条块的质心上，即：

(8)

(9)

式中：ah和av为水平和竖向加速度;g为重力加速度;W为条块重量。惯性效应由上述两个无量纲常数kh和kv来表征。

其中，竖向地震系数kv对边坡稳定性影响很小，相较而言，水平地震系数kh对岛礁岸坡稳定性有很大影响，即便是较小的水平系数也能大大降低岛礁岸坡的稳定性，甚至导致其失稳[21]。因此在稳定水面的条件下，控制竖向系数kv≡0，水平地震系数kh从零逐渐递增，探究安全系数关于水平地震系数变化的敏感性，计算所得结果列于表2，岛礁岸坡安全系数的变化如图7所示。可以看出，随着水平地震系数增大，最小安全系数平滑地逐渐减小，发生滑坡的风险逐渐升高。对比无护岸防波堤的岸坡可知，防波堤有效提高了各级地震荷载作用下岸坡的安全系数，其作为一种风险储备而存在，有利于岛礁工程的长期安全稳定运营。

表2 最小安全系数统计表

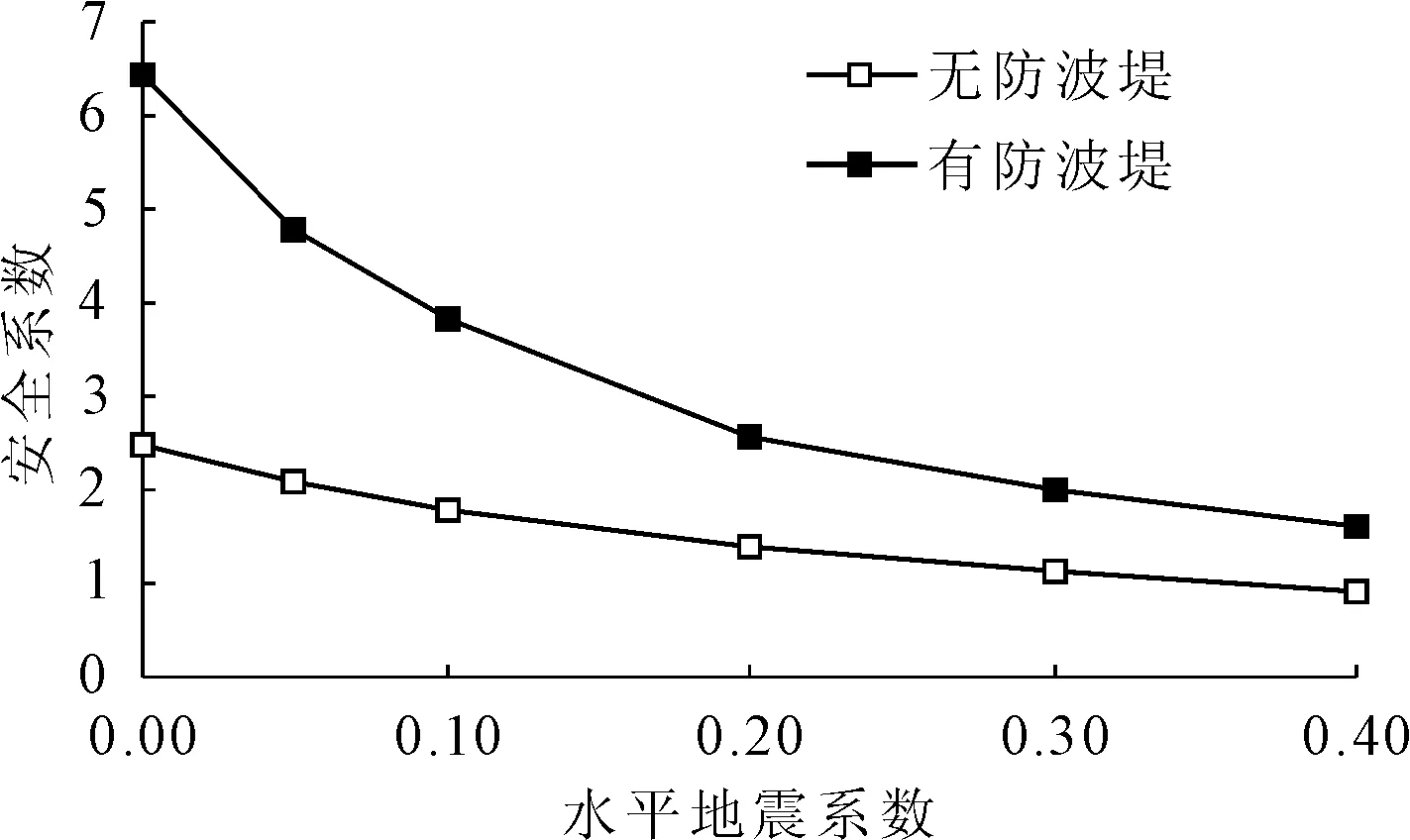
图7 安全系数Fs关于水平系数kh的变化图

3.3 岛礁岸坡地震动力稳定性分析

拟静力分析无法表达安全系数在地震活动这一动态过程中的变化，实际上在某个时刻安全系数可能已经低于临界值。因此，进行岛礁岸坡的地震动力稳定性分析是对拟静力稳定性分析结果的补充和对照；同时，在3.1节，通过累积位移初步判断了岛礁岸坡两种剖面形式的稳定性，直观结论是否正确，应经由动力稳定性分析予以验证。在考虑地震影响时，由于垂直作用对稳定性的影响较小，往往忽略垂直地震作用对海底边坡稳定性的影响[22]，基于此，本文动力分析只施加水平方向的地震动力作用。

在地震动力作用下，临界(或任一非临界)滑动面在每个时间步上的安全系数计算结果如图8所示。当遇到地震时，无护岸防波堤的吹填岛礁岸坡极易发生滑坡，安全系数降低了约60%。故在南海地震多发海域，护岸防波堤具有十分重要的工程意义，保障了岛礁岸坡的安全稳定。

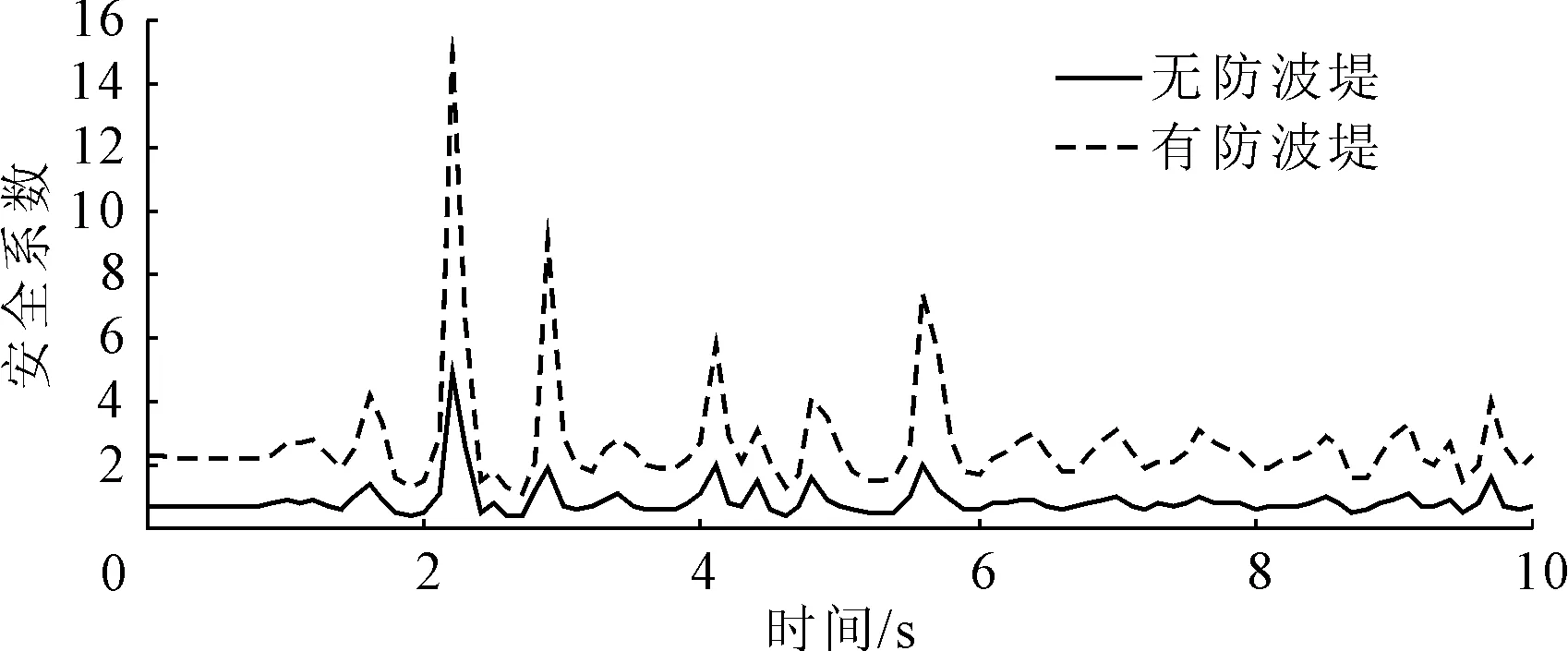
图8 安全系数Fs随时间变化图(10 s)

另外，由图8可得，地震过程中安全系数变化波动很大，动态安全系数难以全面判断岛礁岸坡是否稳定。因此，要针对各单元进行应力状态计算，评价岸坡稳定性。定义新的Slope/W模块分析类型为“地震应力”，以Quake/W模块为上级目录，计算可得到滑移体形态如图9所示，进一步分析岛礁岸坡在地震作用下的稳定性(区别于拟静力法)。无护岸的岛礁岸坡最小安全系数为0.419(见图9(a))，有护岸的岛礁岸坡则为1.677(见图9(b))；安全系数提高了约75%，与拟静力法所得结论一致，即护岸防波堤可以显著提升岛礁工程的稳定性。

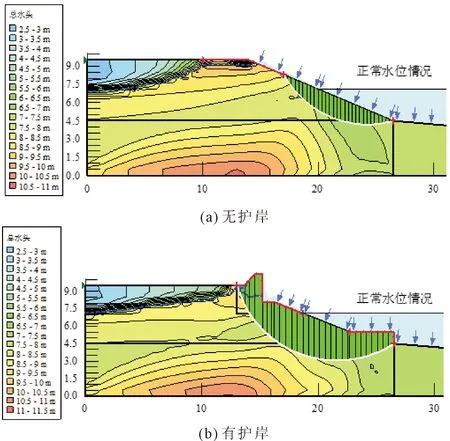
图9 地震作用下岛礁岸坡总水头及稳定性示意图

4 结 论

针对南海典型岛礁岸坡，考虑稳态渗流及非稳态退潮情况下的渗流、波浪力和地震荷载等不同海况开展了岛礁岸坡的稳定性分析，得出以下结论：

(1) 基于海水退潮这一非稳态渗流的水动力过程，岛礁岸坡稳定性会有明显的降低，上部吹填体整体性受到冲击，而护岸防波堤可以有效降低渗流影响，防止吹填体在渗流作用下发生滑塌破坏。

(2) 风暴潮对岛礁岸坡稳定性威胁较大，建设岛礁防波堤有利于降低风暴潮对岸坡的威胁。通过拟静力法等效波浪荷载，对某一极端全表面拉力状态进行稳定性分析，发现无护岸防波堤的岛礁岸坡在极端水位和退潮后正常水位下均无法承受设防波浪的冲击，处于极不稳定状态。

(3) 强震作用对岛礁岸坡稳定性影响很大。通过岸坡随时程变化的震动，对加速度积分所得累积变形可知，未防护的吹填体在强震作用下位移显著，丧失稳定性。拟静力和动力稳定性分析进一步说明，累积变形较大的无护岸防波堤处于失稳状态，护岸防波堤可大幅提升岛礁岸坡在各类极端海况条件下的稳定性。