Recent progress on the reconstruction algorithms of structured illumination microscopy

ZHOU Bo，WANG Kun-hao，CHEN Liang-yi,3,4,5

（1. Insititute of Molecular Medicine, School of Future Technology, Peking University, Center for Life Sciences United by Peking University-TsingHua University, State Key Laboratory of Membrane Biology, Beijing Key Laboratory of Cardiometabolic Molecular Medicine, Beijing 100871, China；2. Key Laboratory of Laser Life Science, Ministry of Education, College of Biophotonics, South China Normal University, Guangzhou 510631, China；3. PKU-IDG/McGovern Institute for Brain Research, Beijing 100871, China；4. Beijing Academy of Artificial Intelligence, Beijing 100871, China；5. National Biomedical Imaging Center, Beijing 100871, China）

Abstract: As an early component of modern Super-Resolution (SR) imaging technology, Structured Illumination Microscopy (SIM) has been developed for nearly twenty years. With up to ～60 nm wavelengths and 564 Hz frame rates, it has recently achieved an optimal combination of spatiotemporal resolution in live cells.Despite these advantages, SIM also suffers disadvantages, some of which originated from the intrinsic reconstruction process. Here we review recent technical advances in SIM, including SR reconstruction, performance evaluation, and its integration with other technologies to provide a practical guide for biologists.

Key words: structured illumination microscopy; super-resolution imaging

1 Introduction

Due to its noninvasiveness and high specificity,fluorescent microscopy is a powerful tool for investigating the structure and function of biological samples[1]. Limited by the diffraction of light, the resolution of conventional fluorescent microscopy is～200 nm and ～500 nm in the lateral and vertical axes[2]and cannot resolve nanostructures beyond the resolution limit. Many Super-Resolution (SR) techniques have been proposed and developed to overcome the resolution limit, and we elaborated on three representative types below, including Stimulated Depletion Microscope (STED), Single-Molecule Localization Microscopy (SMLM) and Structured Illumination Microscope (SIM).

The STED breaks the diffraction limit by illuminating the excited fluorescent molecule with the doughnut-shaped depletion light, which drives the excited molecules away from the center into the ground state[3]. Because only the fluorescence signals emitted from the molecules at the doughnut's center are kept and collected, the effective Point Spread Function (PSF) size of a STED decreases as the intensity of the depletion light increases, resulting in resolution improvement[4].

Based on single-molecule localization accuracy, SMLM appeared in 2006 as fluorescent Photoactivated Localization Microscopy (PALM)[5]and Stochastic Optical Reconstruction Microscopy(STORM)[6], which later become an important category of SR microscopy. The fundamental idea is that if one molecule was imaged, its position could be estimated more precisely than the diffraction limit[7]. Thus, if molecules within the structure could be isolated and imaged one by one, interested nanostructure could be resolved at a much higher resolution once enough molecules are accumulated.

By illuminating the fluorescent sample with a non-uniformly structured pattern, the SIM enables SR imaging by shifting the high-frequency information of the sample into the low-frequency domain of the Optical Transfer Function (OTF) of the microscope[8]. The reconstruction algorithm will extract the high-frequency information and shift it to the corresponding frequency domain; thus, SR-SIM images could be reconstructed from several low-resolution raw images. This review mainly discusses the SIM technique developments, which focused on improving the imaging speed and reducing the phototoxicity for live-cell SR imaging.

2 SIM image formation

Compared to wide-field illumination microscopy, SIM uses non-uniformly distributed lightIex(x) to excite the sampleS(x). The fluorescence light emitted from the sample is collected by the objective lens, wherexrepresents the spatial coordinate. Because of the diffraction, the fluorescence light collection process can be treated as a low-pass filter process and yields the imageIem(x):

Where "·" represents multiplication, ⊗ represents the convolution andPSFem(x) represents the point spread function.

The Fourier transform of equation (1) yields:

Depending on the spatial distribution of the illumination patternIex, SIM either performs a sinusoidal illumination pattern generated by interference(Fig. 1(a)), or a spot-scanning illumination pattern(Fig. 1(b)).

Fig. 1 Schematic diagram of structured illumination microscopy. (a) In sinusoidal illumination microscopy, interference between multiple beams (usually generated by a diffraction grating or spatial light modulator) creates a 2D or 3D striped pattern with spatial frequency kex illuminating on the sample. This pattern shifts the sample's spatial frequency spectrum S(k) to S(k+kex) and S(k-kex), translating high-frequency SR information into the diffraction-limited detection passband OTFem(k) with the spatial cutoff frequency kem. After computational processing, the sample's highest detectable frequency can be extended to k ex+kem. (b) Spot-scanning illumination microscopy where fluorescence is collected by an array detector, and pixels offset by a distance from the excitation spot detect a shifted but higher-resolution,low-signal confocal image. The reconstruction algorithm corrects the shift and restores the signal by reassigning the detected fluorescence toward the illumination axis, with the final resolution P SFsys determined by the product of the excitation PSF ( P SFex ) and the emission PSF ( P SFem). After deconvolution, this process improves resolution similar to that obtained with sinusoidal illumination microscopy

For sinusoidal illumination microscopy, multiple laser beams at the wavelength λexinterfere to generate theIexwith a maximum spatial frequencykex=2NA/λex. Therefore, the high-frequency information of the sampleS˜(k±kex) shifts into theOTFem(k). With multiple orientation/phase illumination followed by the reconstruction, the high-frequency information is unmixed and restored to its proper location in Fourier space. For 2D sinusoidal illumination microscopy with images taken at 3 orientations × 3 phases, 2-fold isotropic lateral resolution enhancement can be achieved.

As for spot-scanning illumination microscopy,the sample is illuminated by the diffraction-limited focusPSFex, which isIex=PSFex. In addition, the fluorescence emission at each scanned position is filtered through a pinhole before being collected by a multi-pixel detector. Thus, the obtained imageIemof a spot-scanned illumination microscopic image can be described as:

whererrepresents the scan position,srepresents the imaging position on the camera,r′represents the sample position andA(s) represents the action of the confocal aperture. Theoretically, after fluorescence reassignment and deconvolution, the lateral resolution of 2D spot-scanning illumination microscopy can be improved to the same extent as the sinusoidal illumination method.

3 SIM reconstruction

As for sinusoidal illumination microscopy, the conventional SIM SR reconstruction algorithm contains two procedures: parameter fitting and reconstruction[10]. The parameter fitting procedure needs to estimate the precise values of the pattern wave vector, the starting phase, and the modulation depth of the illumination light. The cross-correlation of different information components can estimate the pattern wave vector in three steps: (1) standard fast-Fourier-transform-based cross-correlation in frequency space to yield values only at discrete frequency-space pixels; (2) parabolic interpolation to subpixel accuracy to locate the maximum peak of the cross-correlation; (3) refinement through an optimization step in which subpixel frequencyspace shifts along the real-space phase gradients—locating the cross-correlation peak yields the pattern wave vector. After that, starting phase and modulation depth must be estimated accurately,which is crucial because incorrect estimation will seriously decrease the reconstruction quality. A Phase of Peaks (POP) method[11]is proposed by analyzing the POP of the delta function in the spectral space of the spatial frequency of the captured image, which is commonly used in linear SIM but less reliable for high-frequency or low modulation depth illumination patterns. For a high-frequency illumination pattern, Wicker et al. have proposed two alternative methods based on iterative cross-correlation and noniterative auto-correlation reconstruction (ACR) algorithms, respectively[12].For a low modulation depth illumination pattern,Zhou et al. have proposed a reconstruction algorithm based on an Image Recombination Transform (IRT) scheme to determine the initial phase accurately[13]. Finally, after combining the different information components in the frequency domain, a generalized Wiener filter is usually used to reconstruct the SR image.

As an ill-posed inverse problem, conventional SIM reconstruction is prone to artifacts that may decrease the fidelity of SR image reconstruction and perturb its quantitative relationship. Using the prior knowledge of the sample, people have developed algorithms to suppress reconstruction artifacts, such as the Total Variance (TV)[14]and Hessian-SIM[15].TV-SIM is proposed for image reconstruction with a low signal level. The reconstruction process is transformed into an optimization problem by treating SIM as a multichannel imaging system and each channel as an illumination pattern. Reconstruction performance improves by appending a TV regularization constraint to the optimization problem which deviates from the conventional Wiener results because of the suppressed artifacts, which are validated on fixed samples (beads and actin) and live samples (mitochondria). To avoid over-sharpening the boundaries between different regions with the TV regularization constraint, we propose the Hessian-SIM. The Hessian regularization constraint is proposed based on the continuity of biological structures in spatial and temporary dimensions as a priori knowledge to guide image reconstruction. It attains artifact-minimized SR images with less than 10% of the photon dose used by conventional SIM,while substantially outperforming other algorithms at low signal intensities for the time. Hessian-SIM enables rapid imaging of moving vesicles or loops in the endoplasmic reticulum without motion artifacts and with a spatiotemporal resolution of 88 nm and 188 Hz. Its high sensitivity allows sub-millisecond excitation pulses followed by dark recovery times to reduce photo-bleaching of fluorescent proteins, enabling hour-long time-lapse SR imaging of actin filaments in live cells. The authors also observed the structural dynamics of mitochondrial cristae and structures that were not observed then,such as enlarged fusion pores during vesicle exocytosis.

To further increase the effective resolution of SIM for a given photon flux, we take advantage of a priori knowledge about the sparsity and continuity of biological structures to develop a deconvolution algorithm that increases the resolution of SIM nearly to that of two-fold. Our method,Sparse Structured Illumination Microscopy (Sparse-SIM), achieves ～60-nm resolution at a frame rate of up to 564 Hz, allowing it to resolve intricate structures, including small vesicular fusion pores,ring-shaped nuclear pores formed by nucleoporins and relative movements of inner and outer mitochondrial membranes in live cells. Besides the prior knowledge regarding the sample, details of the imaging system may also help. For example,considering the prior knowledge of the sCMOS camera in the SIM imaging system, we proposed an sCMOS noise-corrected SIM reconstruction[16].We established the sCMOS noise model in SIM imaging, and used it to derive an sCMOS noise-corrected SIM reconstruction algorithm which suppresses the sCMOS noise-related reconstruction artifacts and improves the Signal-to-Noise Ratio(SNR).

Besides the regularization constraints based on prior knowledge, PSF engineering is also introduced into High-Fidelity SIM reconstruction (HiFi-SIM) for reconstructing SR images with minimal artifacts and optimal optical sectioning[17]. However,these methods depend onad hoctuneable parameters and may not resolve artifacts associated with different types of sources. To address the issue, Perezet al. proposed a SIM reconstruction method based on a two-step Richardson-Lucy (RL) deconvolution for optimal results without any parameter tuning[18].Smithet al. have proposed a noise-controlled SIM with a physically realistic noise model that explains the structured noise artifact[19]. Therefore, they introduced the True-Wiener-filtered SIM, the flat-noise SIM, and the notch filtering SIM, which suppresses the structured artifacts while maintains resolving power. The benefits of the proposed approaches are demonstrated in focal adhesions and tubulin samples in two and three dimensions and on nanofabricated fluorescent test patterns. All these methods eliminatead hocuser-adjustable reconstruction parameters, thus improving objectivity. However, they also show the trade-off between increasing contrast and suppressing noise, which could be partly overcome by introducing more notch filtering to decrease the SNR.

Unlike these model-driven reconstructions,data-driven approaches, including Deep Neural Network (DNN), provide a new direction for SIM reconstruction. A Generative Adversarial Network(GAN) is used for transforming the Total Internal Reflection Fluorescence (TIRF) microscopy images of subcellular structures within cells and tissues to match the results obtained with a TIRF-based structured illumination microscope[20]. The deep network rapidly infers SR images without any iterations or parameter search, which may democratize SIM imaging. Because GAN is a competitive process between the generator (G) and discriminator (D),two networks must be trained while their losses must be balanced delicately. Therefore, while GAN performs well in image-to-image translation, it is generally challenging to train and requires more input images and training epochs than conventional Convolutional Neural Networks (CNNs). Alternatively, people have proposed U-net to generate highquality SIM images with fewer inputs and lower intensity due to short exposure[21]. The authors of that research have validated its performance on different cellular structures and achieved multicolor, live-cell SIM imaging with significantly reduced photobleaching. A very deep Residual Channel Attention Networks (RCAN) is proposed to avoid hindering the representational ability of CNNs when used in SR tasks[22], and 3D RCAN is developed by modifying the RCAN for 3D applications in fluorescence microscopy[23]. 3D RCAN can improve spatial resolution in SIM using expansion microscopy data as ground truth with some researchers claiming to achieve improvements of ～1.9-fold laterally and～3.6-fold axially.

All existing GAN, U-net and 3D RCAN-based reconstructions are implemented in the spatial domain. However, the difference in frequencies in the Fourier domain rather than structural differences in the spatial domain may enable deep networks to learn the hierarchical representations of high-fre-

quency information more efficiently. Based on this hypothesis, the Deep Fourier Channel Attention Network (DFCAN) and its derivative trained with Generative Adversarial Network (GAN) strategy,termed DFGAN, are proposed and enable robust reconstruction of SIM images under the low SNR conditions[24]. The authors of that research demonstrated that DFCAN achieves comparable image quality to SIM over a tenfold duration in multicolor live-cell imaging experiments, which reveal structures of mitochondrial cristae and nucleoids and the dynamics of interaction between organelles and cytoskeletons.

As for spot-scanning illumination microscopy,the expressionPSFem(s-r′+r)PSFex(r-r′) in Eq.(3) is the product of the excitation point spread functionPSFexwith the shifted emission point spread functionPSFemby an amount -s. If we neglect the Stokes shift between the excitation and emission wavelengths,PSFex=PSFem. Thus the center of gravity of the productPSFem(s-r′+r)PSFex(r-r′) is shifted by -s/2 from the optical axis. Changing this center of gravity toward the optical axis and integrating oversis the reconstruction of spot-scanning illumination microscopy. Because light recorded at pixel positionswith the scan focus at positionris added to the final image at positionr+s/2, the process is referred to as photon reassignment. The photon reassignment can be done either by shrinking the camera image taken at one scan position by a factor of two before adding this shrunken image at center positionrto the final image, or by taking the camera image recorded at scan positionras it is and then adding it at center position 2rto the final image. After applying the photon reassignment to the raw data, the resolution of the reconstructed SR image can be enhanced further by deconvolution algorithms such as Fourier reweighting[25]. The comparison of SIMSR reconstruction algorithm mentioned above could be found in Table. 1.

Tab. 1 Comparison of SIM SR reconstruction algorithm

4 SIM performance evaluation

4.1 Resolution evaluation

The resolution of an optical imaging system represents the ability to distinguish two points of a given distance in an attained image. The first and foremost law of conventional optical imaging science is that resolution is limited to a value on the order ofλ/NA, withλequal to the wavelength of light. Rayleigh and Sparrow captured this law through empirical resolution criteria[27]. These criteria were reiterated by Abbe and Nyquist, who defined resolution as the inverse of the spatial bandwidth of the imaging system. For the SIM imaging system, the resolution depends not only onλandNA, but also on the spatial frequency of the pattern.We have recently developed sparse deconvolution that further improves resolution[26]. Despite these advances, evaluating a system's resolution without bias is crucial.

By evaluating the similarity between two independent reconstructions of the same object in frequency space to determine the threshold (the spatial frequency) at which two reconstructions are consistent with each other. Fourier Ring Correlation (FRC)is a method commonly used to determine the imaging system resolution[28]. The object is considered to be resolved up to this spatial frequency. To compute the FRC resolution, two statistically independent SR reconstructed SIM imagesandare required, wheredenotes the spatial coordinates. Subsequent statistical correlation of their Fourier transformsandover the pixels on the perimeter of circles of constant spatial frequency with magnitudegives the FRC:

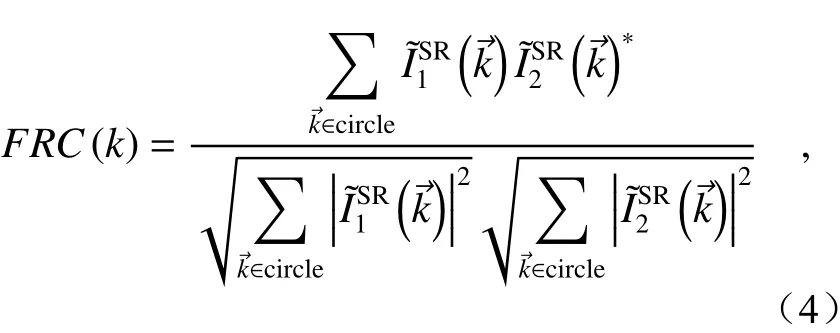
where "*" denotes the conjugate operation. At low spatial frequencies, the FRC curve is close to unity.At high spatial frequencies, noise dominates over signal; thus, the FRC decays to 0. The image resolution is the inverse of the spatial frequency for which the FRC curve drops below a given threshold[28].Different threshold criteria are proposed and evaluated (0.5, 0.143, 2σ)[29-30], and a fixed threshold of 1/7≈0.143 is found to be practical for SIM[19].While FRC can only be used to evaluate the resolution of the 2D image, Fourier Shell Correlation(FSC) must be used to evaluate resolution in 3D. By substituting the ring and 2D Fourier transform in FRC with a spherical shell and a 3D Fourier transform, FSC is turned into a generalization of the FRC.

Two statistically independent SR images are required to compute the FRC/FSC resolution of SIM, which can be achieved by acquiring consecutive images under the same conditions. However,due to the bleaching or temporal fluctuations of the fluorescence signals in live-cell experiments, the assumption that FRC/FSC is stationarity may not be valid[31]. Furthermore, the empirical criteria for determining the threshold in FRC/FSC confers a problem. A new method based on partial phase correlation called decorrelation analysis is proposed for resolution estimation. The decorrelation analysis does not rely on user-defined parameters and only requires an individual image. The main decorrelation analysis algorithm is divided into two steps.First, the cross-correlation between the Fourier transformof the SR reconstructed SIM image and its normalized versionis computed. By repeating operation where the normalized Fourier transform is filtered additionally by a binary circular maskof radiusr,the decorrelation functiond(r) is computed by:

In general, the decorrelation functiond(r) will exhibit a local maximum of amplitudeA0that indicates the spatial frequencyr0of best compromise of rejecting noise and preserving signals. Reducing the mask further removes signals than noise, thus decreasing the correlation belowA0until it drops to 0 forr= 0. Thus the positionr0of the local maximum is therefore related directly to the spatial frequency distribution of the image. The input image is subjected to a total ofNghigh-pass filterings (from weak to robust filtering) to attenuate the energy of low frequencies. For theithfiltered image, a decorrelation functiondi(r) is computed once the peak positionriand amplitudeAiare extracted, generating a set of [ri,Ai] pairs. If the high-pass filtering removes too much signal, the decorrelation function will not exhibit a local maximum, and the peak position and amplitude will be set to 0. Therefore, the estimated resolution is computed by 2P/max{r0,···,rNg}, wherePdenotes the pixel size. Because the decorrelation analysis algorithm estimates the highest frequency from the local maxima of the decorrelation functions, it enables parameter-free image resolution estimation based on an individual SR reconstructed image.

4.2 Artifacts evaluation

Conventional SIM is prone to noise-specific artifacts that limit its applicability for lower signal-tonoise data[19]. The simplest way to quantify artifacts is to compare SR-SIM images with the corresponding diffraction-limited counterparts directly. According to this idea, the SR Quantitative Image Rating and Reporting of Error Locations (SQUIRREL)is presented as an analytical approach that allows the quantitative mapping of local image artifacts[32].

SQUIRREL is based on the premise that an SR image should be a high-precision representation of the underlying nanoscale positions and photon emission of the imaged fluorophores. The algorithm requires three inputs: a reference image (generally diffraction-limited), an SR SIM image, and a representative Resolution Scaling Function (RSF) image.The RSF can be provided by the user or automatically estimated through optimization. Assuming an imaged field of view has a spatially invariant Point-Spread Function (PSF), applying RSF to the SR images should produce an image that is highly similar to the original diffraction-limited version. The variance between these images beyond a noise floor can be used as a quantitative indicator of local artifacts in the SR representation.

The process of estimating an artifacts error map via SQUIRREL is divided into 3 subsequent steps and described below. The following notation will be used to denote the different images during this process.ID: diffraction-limited reference image;RS F: resolution scaling function;IRSF: resolution scaling function integrated over finite pixels;IS: original SR image;IS T: SR image registered to reference image;IS Tγ: registered SR image following linear intensity rescaling.

(1) Benchmarking the SR reconstruction against the reference image

The first step of registration is the estimation of the lateral mismatch Δx,Δy, through cross-correlating the reference and the SR images. The translation is needed to correct for aberrant shifts in the SR imageISarising from uncorrected sample drift and differences between the optical path used to collect the reference diffraction-limited imageIDand SR imageIS, or from offsets introduced by the reconstruction processes. For this purpose, the cross-correlation is calculated through a Fast Hartley Transform (FHT), taking advantage of the threaded Parallel Colt library. Δx, Δycan then be estimated by calculating the spatial difference between the coordinates with the matrix correlation peak and its geometric center. The correlation matrix is also up-sampled via a bi-cubic spline interpolation. Finally, bi-cubic spline translation is employed in the SR imageISfor maximizing its overlap with the reference image to produceIS T. Thus,IS T=IS(x-Δx,y-Δy).

(2) Image intensity rescaling and the RSF estimation

This step is to rescale the intensity of the SR estimate linearly imageIS, and to convolve it withIRSFin a manner that will maximize the similarity of its intensity range to that of the reference imageID.The unknown variables α and β that define the intensity rescaling need to be estimated to generateIS Tγ. ThusIS Tγ=αIS+β.

Additionally, the SQUIRREL algorithm can automatically estimate the RSF by approximating to a 2D Gaussian function of an unknown standard deviation σ through a highly threaded implementation of a Particle Swarm Optimizer (PSO). And the joint optimization problem is defined as:

(3) Calculating the error map, RSE, and RSP

The process of artifacts error mapping starts with the calculation of the imageIRScreated by applying the RSF to the SR image. Thus,IRS=

The global similarity betweenIRSand the reference diffraction-limited imageIDcan be calculated through a root-mean-square error, named RSE for Resolution Scaled Error, and a Pearson correlation coefficient, called RSP for Resolution Scaled Pearson coefficient, thus

whereandrepresents the average value ofIDandIRS, respectively.

The artifacts error mapMis the pixel-wise absolute difference betweenIDandIRS, thus

4.3 Modulation contrast evaluation

The intensity of the modulation contrast (or stripes) in the sinusoidal illumination microscopy raw image is a crucial determinant of SR reconstructed image quality, as it critically affects the amount of frequency-shifted information that can be reassigned in the reconstruction process. To measure the contrast of local stripes, each voxel in a raw 3D image is calculated as follows[33]:

(1) A variance stabilizing Anscombe transform(Anscombeet al. 1948) is performed so that noise follows an approximate Gaussian distribution, rather than Poissonian distribution.

(2) Az-window is selected where 2z+1 (zrepresents the number ofz-planes above and below to be combined with eachz-plane), and all raw phase images within this window are stacked (the defaultz-window of ±1z-sections increases the signal-tonoise ratio to a similar extent to the "band filtering"performed during reconstruction). These phase series are Fourier-transformed using a multithreaded 1D discrete Fourier transformation along the dimension of the different phases. The result of this 1D Fourier transformation allows the separating of the raw data's different frequency components.

(3) The power of the frequency components corresponding to the illumination pattern modulation is divided by the standard deviation of the highest frequency component for the samez-plane(taken to be dominated by noise). The frequency components of the first- and second-orders in the Fourier transformed stack are located at plane numbersLFTO/Np+1, whereLFTrepresents the length of the above Fourier transformed data stack,Nprepresents the number of phase shifts during data acquisition, andOrepresents the order number (1 or 2). The modulation-contrast-to-noise-ratio value is calculated asThe average modulation contrast for each channel can be estimated using the Otsu algorithm to threshold the histogram.

Furthermore, by multiplying the intensity of each pixel by its MCNR value, the Modulation Contrast Map (MCM) can be computed. The MCM is an RGB image where the mapped color of reconstructed features indicates the underlying modulation contrast in the corresponding raw data. A summarization of the SIM performance evaluation algorithm in this section could be found in Table. 2.

Tab. 2 Summary of SIM performance evaluation algorithms

5 SIM integration with other technologies

5.1 TIRF-SIM

For conventional SIM, the wide-field illumination excites fluorophores beyond the focal plane.The significantly out-of-focus illumination causes photo-bleaching/photo-toxicity, limiting the systems'temporal resolution, imaging duration, and SNR. In Total Internal Reflection Fluorescence (TIRF) microscopy, an evanescent field selectively excites fluorophores adjacent to a coverslip (＜100 nm),which effectively eliminates out-of-focus fluorescence[34]. Integrating TIRF with 2D SIM enables sub-diffractive imaging with superb background rejection and low photo-toxicity.

As for 2D sinusoidal illumination microscopy,a video rate TIRF-SIM imaging (Fig. 2(a), color online) of tubulin and kinesin dynamics in living Drosophila melanogaster S2 cells is demonstrated with 100-nm resolution at frame rates up to 11 Hz[35].Equipped with an ultrahigh numerical aperture (NA,1.7) objective, a TIRF-SIM achieves an 84-nm resolution at sub-second acquisition speeds in living COS-7 cells. With multicolor capability, it is used to visualize the individual Clathrin-Coated Pits (CCPs)and their relationship to cortical F-actin near the basal plasma membrane[36]. By reducing the illumination angle in traditional TIRF-SIM for grazing incidence excitation, GI-SIM[37]and its multicolor version[38]mildly extend illumination depth down to 1 μm, while presumably improving contrast compared to regular 2D-SIM. However, the advantage of GI-SIM compared to regular 2D-Sparse SIM is not apparent, given that the latter method can clearly reveal organelles in deep cytosols, such as nuclear pores in live nuclear membranes[27].

As for spot-scanning illumination microscopy,multifocal SIM utilizes the Digital Micromirror Device (DMD) to generate sparse multifocal illumination patterns and physically rejects out-of-focus light. This enables subdiffraction imaging in live samples eightfold thicker than in previous experiments on whole cells at 1-Hz frame rates[39]. An analog implementation of multifocal SIM, instant SIM,utilizes optical instead of digital image-processing operations to increase data acquisition rates, achieving 145 nm lateral and 350 nm axial resolutions at acquisition speeds up to 100 Hz (Fig. 2(b), color online)[40]. The power of instant TIRF-SIM is demonstrated in imaging fine, rapidly moving structure including motor-driven organelles in human lung fibroblasts and the cytoskeleton of flowing blood cells within developing zebrafish embryos.

Fig. 2 The schematic diagram of TIRF-SIM (a) and instant SIM (b). Adapted from Kner et al.[35] and York et al.[40]

5.2 Two-photon-SIM

Upon imaging thick samples, SIM is suspect to increased scattered emission and background noise,which decreases the spatial resolution and SNR.With better penetration ability offered by the long excitation wavelengths, two-photon (2P) excitation can help alleviate these issues. 2P excitation is often combined with spot-scanning illumination microscopy but not sinusoidal illumination microscopy. This is because sinusoidal illumination microscopy is prone to local scatters within a sample.Under such circumstances, globally determined parameters are incorrect and will produce reconstruction artifacts that cannot be resolved[41].

An early implementation of 2P-SIM uses a multifocal excitation pattern (Fig. 3(a), color online), which requires the post-processing of hundreds of raw images to reconstruct each 2D SR image. It gives resolution-doubled images with better sectioning and contrast than 1P excitation in thick scattering samples such as Caenorhabditis elegans embryos, Drosophila melanogaster larval salivary glands,and mouse liver tissue[42]. With a single 2P excitation focus in rescan confocal geometry (Fig. 3(b),color online), 2P instant SIM (2P-ISIM) provides an improved frame rate and even lower background noise[43]. 2P-ISIM offers a spatial resolution of～150 nm laterally and ～400 nm axially and a frame rate of ～1 Hz at depths exceeding 100 μm from the coverslip surface in thick samples. The capabilities of 2P-ISIM are demonstrated by imaging whole nematode embryos, larvae, tissues, and organs inside zebrafish embryos. Incorporating the resonant scanner improves the frame rate of 2P-SIM to 30 Hz,and enables imaging of actin cytoskeleton within human mesenchymal stem cells, rat tail collagen I hydrogels and nuclei deep within living Drosophila melanogaster embryos (Fig. 3(c), color online)[44].

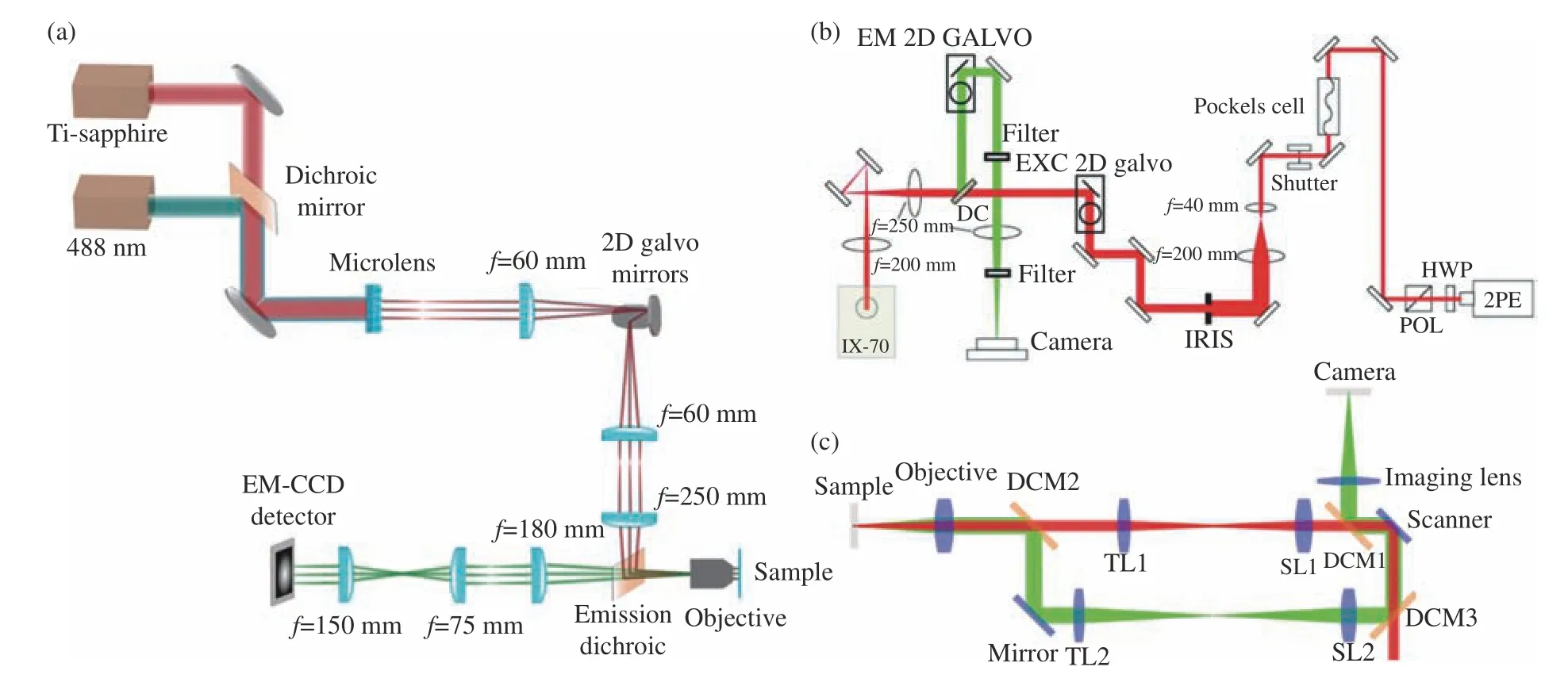
Fig. 3 Schematic diagram of early implemented 2P SIM (a), 2P-ISIM (b), and 2P SIM with the resonant scanner (c). Adapted from Ingaramo et al.[42], Peter et al.[43] and Gregor et al.[44]

While, the high peak intensities in 2P excitation might cause more photo-toxicity and confound the long-duration imaging ability of 2P-SIM imaging, the spectral match between laser sources and fluorescent probes might limit the multicolor imaging of the system. Furthermore, the high costs of 2P laser sources may be another practical concern worth considering with this technology[9].

5.3 Nonlinear-SIM

Because the pattern formed by the interference is also diffraction-limited, SIM can only increase resolution by twofolds. However, if fluorescence emission depends nonlinearly on the illumination,Higher-Order Harmonics (HOH) are introduced into the illumination pattern with(η＞1). The spatial resolution can be extended to approximately λ/2NA(η+1). Therefore, an infinite number of HOH would theoretically lead to unlimited resolution. An early implementation of non-linear SIM was proposed in 2002[45]. With a peak excitation energy density of 37 mJ/cm2, five detectable HOH and ＜50 nm spatial resolution can be achieved by saturated SIM[46]. Because saturation excitation requires extremely high illumination intensities that lead to accelerated photo-bleaching and photo-damage even in fixed tissue, this implementation is a theoretical demonstration of resolution increase.Still, it cannot be used to study biological samples.

Interestingly, with structured STED enhanced by surface plasmon resonance, a non-linear SIM based on STED is considered suitable for live-cell imaging[47]. Simulation analysis predicts that SPRenhanced 2D STED is strong enough for non-linear SIM to achieve high-speed imaging at a 30-nm resolution and single-molecule sensitivity. Structuredexcitation STED-SIM (SSTED-SIM) is proposed to increase non-linear efficiency and imaging depth,which has structured excitation light and STED light with the same grating vector in the sample plane.The optical resolution, feasibility, and background fluorescence reduction of SSTED-SIM are numerically simulated[48]. For three-dimensional (3D) SR imaging over a volume, 3D STED-SIM (Fig. 4, color online) is proposed[49]. Using structured illumination to generate a 3D depletion pattern, 3D STEDSIM can achieve 60 nm lateral and 160 nm axial resolution at a 5 Hz volume rate with reduced photo-bleaching and photo damage.

Fig. 4 (a) Schematic diagram of 3D STED-SIM. (b) The cross-section comparison of lateral PSF (top, left), axial PSF (bottom, left), lateral OTF (top, right), and axial OTF (bottom, right) of the widefield microscopy (red) and 3D STED-SIM(blue). Adapted from Xue et al.[49]

Reversible photo-switching of a fluorescent protein provides the required nonlinearity at light intensities six orders of magnitude lower than those needed for saturation excitation. A non-linear SIM based on the reversible photo-switching fluorescent protein demonstrates approximately 40-nm resolution on purified microtubules labeled with the fluorescent photoswitchable protein Dronpa, and enables mammalian nuclear pores and actin cytoskeleton to be visualized[50]. However, the switching scheme in the study is highly inefficient because only a small fraction of the fluorescence from photo-switched molecules contributes to final reconstruction. To compensate for the deficiency, a more efficient switching scheme is proposed, including patterned activation, excitation, and readout[36]. A photoswitchable protein (Skylan-NS) is used, which offers enough switching cycles before photo-bleaching, a sufficient photon number per switching cycle, and a high contrast ratio between the on and off states.The PA NL-SIM can yield 62-nm lateral resolution and a sub-second frame rate with 25 raw images and a 20～100 W/cm2intensity. Further saturation of the partial molecules in the activated state (saturated PA NL-SIM) can achieve a near-isotropic lateral resolution of 45 nm with 35 raw images and a 490 W/cm2intensity. These approaches are applied to image dynamics near the plasma membrane of spatially resolved assemblies of clathrin and caveolin, Rab5a in early endosomes, and α-actinin with cortical actin.Although non-linear SIM fills the gap between the～100-nm resolution of linear SR-SIM and the ～20-nm resolution of SMLM and STED, non-linear SIM in live cells is still limited by imaging duration and rate. Further development in photoswitchable dyes may help to break these limitations. On the other hand, using the computational SR algorithm we developed, Sparse-SIM achieves ～60-nm resolution with only 9 raw images, has normal fluorophores,and has good live-cell compatibility[27]. Because the deterministic deconvolution algorithm can extend the resolution of SIM and other fluorescence microscopes beyond their resolution limits posed by optics and fluorescence probes, it represents an alternative direction of pushing the spatiotemporal resolution in general.

6 Summary

SIM has been widely used in life sciences for its high specificity and non-invasive imaging ability.In this review, we introduce the recent developments of SIM from multiple aspects, including the SR reconstruction algorithm, performance evaluation, and its integration with TIRF, two-photon and non-linear technologies. With the developments in optical design, better detectors, new dyes, and reconstruction algorithms, SIM will be more powerful for revealing structural and functional dynamics in live cells.