基于二次分解组合预测模型的高速铁路短期客流预测＊

高立东，白军成

（1.兰州交通大学交通运输学院,甘肃 兰州 730070；2.西安电子科技大学经济管理学院，陕西 西安 710071）

1 引言

随着我国城镇化水平的提升以及社会经济发展水平的持续增长,选择高铁为旅行方式的乘客正逐步增多。乘客是交通运输的主体,科学地预测客流量,对旅客列车开通以及客运组织方案的制定都有着很大的现实意义。高铁短期客流预测其实就是对日乘坐高速铁路出行的旅客数量的预测统计,在一定程度上可以很直观地显示高铁客流在短期内的变化态势以及以此推断出来旅客数量的未来变化趋势,而取得稳定且较为准确的客流预测也可以给乘客创造更为便捷的条件和更加良好的服务质量。

随着铁路交通客流量预测理论的深入研究,在中长期客流预测领域中已经有很多学者都做过相关的研究，可以说成果颇多，但相比之下短期客流方面的研究还有待发展，近几年短期客流量预测的新方法被日益提出。在交通客流量预测方法中，传统的数理统计学方法最先被运用其中，例如Sangsoo等[1]对ARIMA模型做出了详细的解析,在文中将影响高铁客流的时间、空间，以及社会经济因素等统统考虑进来，从而达到比较全面对预测模型性能的探讨研究，并最终得到的预测结果表明该论文中的思路方法有很不错的借鉴价值。Jonas[2]创立的模型要区别于一般的回归类模型，是一种多元的回归预测模型,用来预测客流量，在文中具体实验结果表明预测值的偏差减少了并且输出结果较稳定。但这些方法学习能力一般,面对实际问题中数据的复杂性通常预测精度和稳定性会受到较大的影响，且此类模型很难抓住非线性动态数据的特征,所以实验结果的预测精度还有待提高。人工智能技术的深入研究应用目前在很多领域都比较常见，在预测方面已经熟知的方法中包括有支持向量机、前馈神经网络系统以及相关结合生物算法的神经网络等。人工智能技术的特点可以总结为模仿人类大脑认知和推演的过程,具体表现为通过结合数据的时间和空间特征参数来构建相关模型,同时可以在没有任何先验知识的情况下以任意精度逼近任何非线性模式,所以其能被广泛地应用到铁路、航空等的客流预测领域中，为旅客出行提供了重要参考依据。邓军生等[3]探讨分析了几种预测模型，对比各模型预测结果的评价指标，得出支持矢量回归机（SVR）的客流预测模型在各方面都具有优越性,运用该模型开展的实验研究其实验结果表明构建模型的预测性能相对最好。韩媛媛等[4]将时间序列信息解析基础理论和信息挖掘技术相结合,利用构建了采用信息挖掘新技术的径向基神经网络模型进行客流预测,将结果和采用BP神经网络模拟的预测结果比较,显示预测效果良好。极限学习机的提出表明，其在各方面相较传统的神经网络性能优异[5]。具体由于输入权重和偏置随机产生,使得模型的泛化性能和学习速度都大大提升,进而使得非线性拟合能力表现更加突出。此外,在这一基础上核极限学习机也被提出，它的预测性能有所改善，主要因为它相较极限学习机可以利用核函数来替代原先的激活函数，以此提高整个模型的预测性能，且在短时客流预测方面得以良好应用。

因为人工智能技术需要初始化权重和阈值,所以其参数设置的复杂性使得无法保证持续输出稳定的预测结果。在短期客流量预测研究大发展的背景下,组合类预测模型开始被学者探讨研究，成为了短时客流预测研究的重点方向之一。在高铁客运领域,因为一般原始客流数据波动性很强,所以在此基础上得到的客流量预估会出现预测结果与实际值误差较大的现象。学者们通常利用数据预处理技术来极大程度减小复杂数据带来的预测不稳定的问题，并相应提高预测准确性。比较常见的处理技术有很多，其中小波包分解和变分模态分解就是学者使用较多的、经验模态分解也随着发展逐步更新有了完全重组经验模态分解算法的创新。利用这些分解方式可以达到使原有时间序列自适应地分解成一些较为平稳的子序列的效果，这样再进行预测时得到的预测结果更准确且稳定性也有所提升。例如Yu等[6]使用EMD方式对地铁的短期旅客流量做出分解处理,并在此基础上建立了短期客流量预测模型，实验结果表明该模型有很大参考价值，尤其是它启发了考虑利用分解组合的模式来建立模型进行客流预测实验是非常有效的方法。杨军和侯忠生[7]分析了北京站的具体车站客流量情况，其中对各个时间间隔下的乘客出行人数做了详细统计,并运用小波分解对数据做出了分解处理,从而减弱了其不规则的波动性态势,同时结合支持向量机对车站的客流量做出了预测,最后经过测试证明了预测结果良好，且该方法模型创新使用的效果得以显现。潘杉[8]分别对比了EEMD-ARIMA、EEMD-SVR、ARIMASVR等模型在铁路客流量预测实例中的效果,得出结论即EEMD算法对原始数据的分解起到了关键的作用，它让客流数据分解为IMF分量形式再输入预测模型结构中，这样有效提高了实验结果的预测准确性，同时突显了组合预测模型预测性能稳定和适用性强的良好特点。何九冉和四兵锋[9]分析了北京地铁的历史客运量数据,针对日客流量有着不稳定变化规律特点，构建了EMD-RBF客运量预测模型,得到的日车站客流量预测值具有很好的精度，说明利用分解分量来预测的EMD-RBF预测模型方案可以很好改善预测结果的精确度和稳定性。

2 研究方法

高速铁路的短期客流时间序列会同时受到时间、空间等多个随机变化因素的综合影响,并且在一定程度上表现为很大的波动性。论文中采用引入相关分解模型对高速铁路客流时间序列进行初步分解的方法,并通过综合分析高铁短期客流对应在各个时间尺度下的波动特征来更全面挖掘出客流数据变化规律背后隐含的信息，以此来揭示高铁短期客流量变化的发展趋势。

2.1 经验模态分解

经验模态分解（EMD）算法对于解决信号时频处理相关问题十分有效,具体表现为它可以自适应地进行对信息特征识别并筛选的过程[10]。对比传统傅里叶变换方法,它没有预先确定任何基函数,仅对时间序列自身的波动发展趋势加以分析。它能够把复杂时间序列进行分解，使原来的复杂序列变为有限个本征模态函数，这样以分量形式的再预测,可以充分挖掘原始数据背后的大量隐含信息,同时使得复杂波动的数据更为平滑化，便于后续预测模型的训练。因而该方法在非线性非均匀时间序列的问题解决中开始应用较多。针对本文的高铁客流数据序列,其EMD的具体实现过程为:

（1）找出原始序列X（t）中的局部极大值，然后用三阶样条函数进行插值，得到原序列上下包络值Xmax（t）和Xmin（t）；

（2）对每一个时间段的Xmax（t）和Xmin（t）取均值：

（3）类距平均值序列h（t）：

如果h（t）中跨零点的数目和极值点的数目小于等于一个，就得到了内模函数；否则，继续上面的步骤。用原始序列X（t）减去I1（t）得到剩余值r1（t）：

重复直到没有IMF能够被提取出来。

2.2 完全重组经验模态分解

对经验模态分解模型来说,它本身就在信息处理中具有一定缺陷,即是由于信息中断而导致的模态混叠现象。这对预测精度有着十分不好的影响。

Wu和Huang[11]为解决这一问题，在EMD方法的基础上提出了给原始数据加白噪声的方法,从一定程度上减少了EMD中的模态混叠现象。但是又因为增加了大量白噪声,它所形成的残余会对原始数据产生其他污染,因此为减少由于增加白噪声所产生的影响,Torres等[12]在EEMD的基础上提出了完全重组经验模态分解（CEEMD）方法,把一对正噪声和负噪声都加入到了初始信号中,这样通过抵消的方式以降低分解过程造成噪声残留带来的干扰。其中具体CEEMD描述如下:

（1）原始数据加入噪声Z1和Z2；

A表示原始数据；E是添加的噪声；表示添加了正噪声的数据序列；Z2表示添加了负噪声的数据序列。

（2）噪声序列Z1和Z2被EMD 分解成2个本征模态函数集合；

（3）重复上面的步骤直到残余项成为一个单调递增函数；

（4）得到最终的本征模态函数集合。

2.3 变分模态分解

Dominique[13]提出的变分模态分解（VMD），其具体实现过程为假定各模态分量为uk，且对模态函数设置中心频率为ωk，为使uk的有限带宽在中心频率ωk的规定范围内，需作如下处理：

（1）对每个uk进行Hilbert变换得到单边频谱；

（2）将频谱转移到基带；

（3）每个uk带宽由L2范数梯度的平方估算可得。

综上，可得约束变分问题模型如下式所示：

在式（6）和（7）中：k 为迭代次数；δ（t）为脉冲函数；f（t）为待分解信号；i为虚部。

为求得最优解，得到增广拉格朗日表达式：

式（8）中：α为平衡参数。

2.4 样本熵

样本熵是被在近似熵的基础上提出的一种模型算法，它提高了熵值测量的精确度,并且降低了误差[14]。它可以对非线性数据的复杂性指标进行合理评估。其中整个序列的复杂度如果越高那么它对应的熵值越大，相反。详细计算步骤如下：

（1）重构原始数据形成一个矩阵：

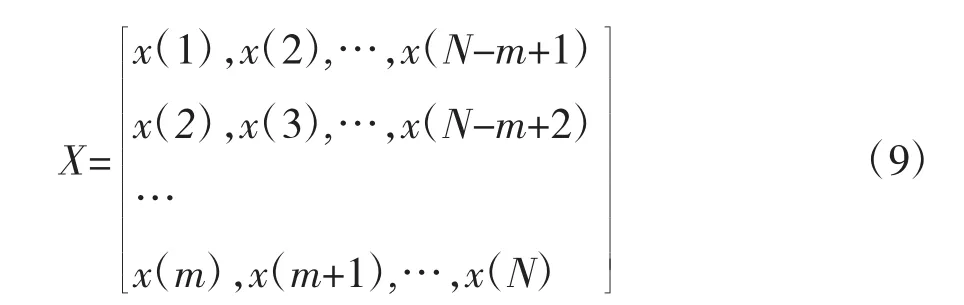
（2）定义变量x（i）和变量x（j）之间的距离d[x（i）,x（j）]：

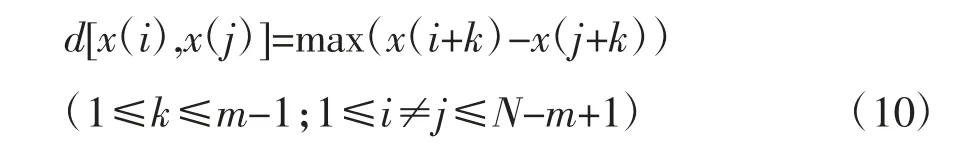
（3）给定阈值r，然后记录满足条件d[x(i),x(j)]≤r的数量Ai（r），记做：Aim（r）

第二，福建小学教育经费的持续增加，也缓解了战时小学教育的压力。1940年福建省的国教经费为994014元，1941年增为1254897元［28］73；1942年全省教费列为10198450元，其中国教经费2079302元，到1943年，全省教费列为14944589元，国教经费2295768元［27］3。就这四年而言，国教经费就增加了1301754元。由于福建省对小学教育经费的增加，在一定程度上促进了小学教育的发展。

（4）计算Aim（r）的均值Am（r）：

（5）更新m，重复步骤（1）到（3），然后得到Am+1（r）

（6）计算样本熵值：

2.5 极限学习机与核极限学习机

Huang[10]提出的极限学习机(ELM)对比其他传统前馈神经网络，各方面优势都较为突出。鉴于此,该方法已被许多专家学者研究应用于多个领域[15-16]。

对于n个任意（xi,yi）的样本，其中xi∈R，yi∈R，i=1,2…，n，单层前馈神经网络构建如下：

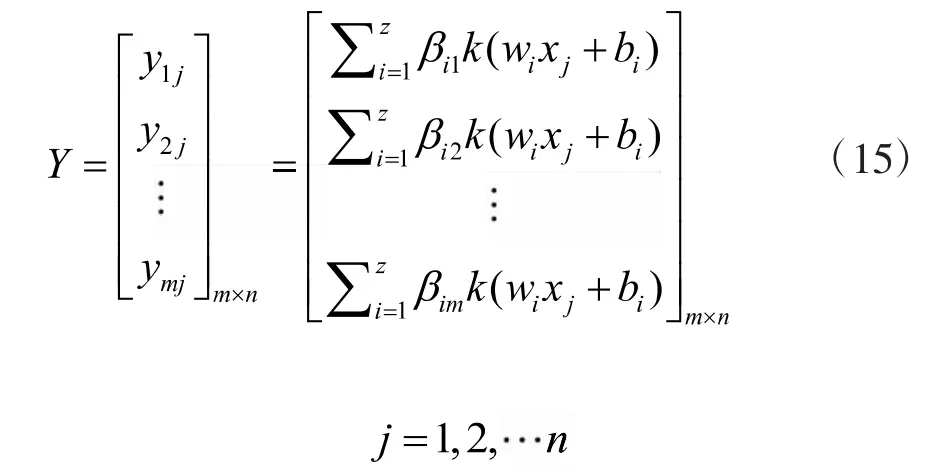
式中：Y代表输出矩阵，β表示极限学习机的权值，W表示输入权值，z代表隐含层的节点数，公式（15）简写如下：

上式的解可由下面的计算得到：

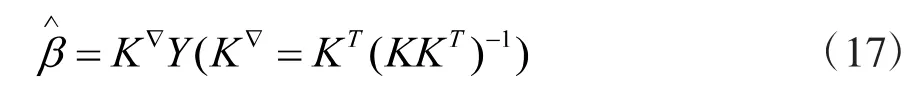
利用核函数取代原来的激活函数k（x）,即可得到核极限学习机，具体如下:

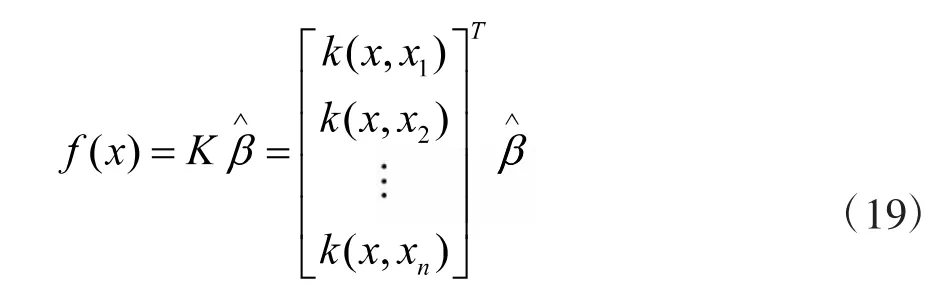
2.6 CEEMD-ELM-VMD-KELM模型

为了提高高速铁路短时客流量时间序列的预测精度,提出了一种新型的CEEMD-ELM-VMDKELM组合预测模型。因为通常在进行客流预测时,原始数据序列内在噪声的干扰会很大程度影响预测结果，使得预测输出结果的稳定性和精确度都受到影响。本文将充分利用数据预处理技术来减少噪声影响,并且在传统一次分解之后，进行对较复杂序列的再次分解,这样让一次分解后得出的高频分量可以被再一次分解来降低分量的预测难度,从而达到对最复杂分量进行平滑处理的目的,同时减少整体数据的复杂性并更好地利用IMF分量预测模型方案，具体步骤如下:

步骤一：对原始客流量数据进行CEEMD分解；

步骤二：引入样本熵模型对一次分解分量的复杂度进行计算判断；

步骤三：选择复杂度最高的分量进行二次分解,在充分降低数据复杂度的同时也更好地挖掘时间序列中的隐藏信息；

步骤四：再次使用样本熵测量二次分解分量的复杂度；

步骤五：通过分析确定预测模型的输入个数；

步骤六：建立基于极限学习机的短时客流预测模型，用来预测除最大SE值序列以外的一次分解分量，以及使用基于核函数的极限学习机来预测二次分解分量；

步骤七：将所有预测结果相加求和。

3 实例分析

本研究以ZD013-ZD190-01的OD 日客流作为原始数据，预测时划分训练集和测试集，其中选择样本共145个（2015 年1 月1 日—2015年5月25 日）作为训练集，样本36个（2015年5 月26 日—2015 年6 月30 日）作为测试集。通过对前145项数据进行模型训练，将训练好的模型用于其后测试集的预测。基准模型中，将高铁的日客流量数据分别带入BP神经网络、Elman神经网络、ELM和KELM等模型进行实例检验和分析比较。随后在组合模型中，构建出一次分解组合预测模型，然后对生成的各预测数据及对应评价指标进行对比分析。最后在一次分解基础上进行二次分解，构建出二次分解组合预测模型，通过预测结果比较各模型的预测性能以确定出最终的预测模型方案。

3.1 基准预测模型

分别以BP神经网络、Elman神经网络、ELM和KELM为基准预测模型，输入原始数据，运用各基准模型进行训练学习，可获得预测结果。

本章通过采用平均绝对值百分比误差（MAPE）、均方根误差（RMSE）和平均绝对误差（MAE）来评价各模型的预测性能。在此基础之上，还引入了Dstat作为重要的衡量方向程度的标准。

其中MAPE、MAE和RMSE的值越小，说明预测模型表现越良好。而对Dstat来说,数值越大说明预测效果越好。具体对应各模型的预测效果见表1。

表1 基准模型预测效果对比

从表1中可以看出，用4种基准模型预测高铁日客流量时，ELM和KELM预测模型的相关指标接近，且前三项指标都较小，Dstat值较大，这说明ELM和KELM预测模型的预测效果优于BP和Elamn神经网络。参考其他文献[17-22]，该类基准模型在预测精度方面还有改善提升的空间。

3.2 基于二次分解的组合预测模型

由于高速铁路客流量具有非线性、非平稳性的特点，BP神经网络等基准模型在预测时，那些波动性强的复杂数据会对整个网络产生干扰，致使预测精度受影响。因此通过CEEMD算法和VMD算法分别进行一次，二次分解，可逐步降低原始数据的波动性和复杂性，结合基准模型ELM和KELM，可形成CEEMD-ELM-VMD-KELM的二次分解组合预测模型。

3.1.1 预测模型构建

首先，通过对原始客流量数据进行CEEMD分解,且如果分解后得到的模态数量过多会导致偏差的积累,从而使得预测效果较差;如果分解得到的模态数量过少,又说明有效信息没有完全挖掘,因此本文将数据分解为8 个本征模态函数。然后用样本熵模型计算比较得出最复杂的分量进行VMD二次分解，同理分解后获得8 个本征模态函数，且所有分解结果显示在图1和图2，熵值计算结果见表2和表3。

表2 CEEMD分解子序列的样本熵值

表3 VMD分解子序列的样本熵值

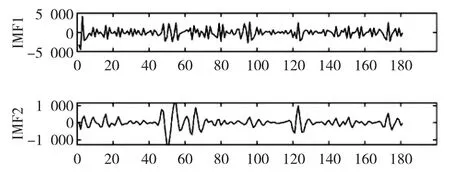
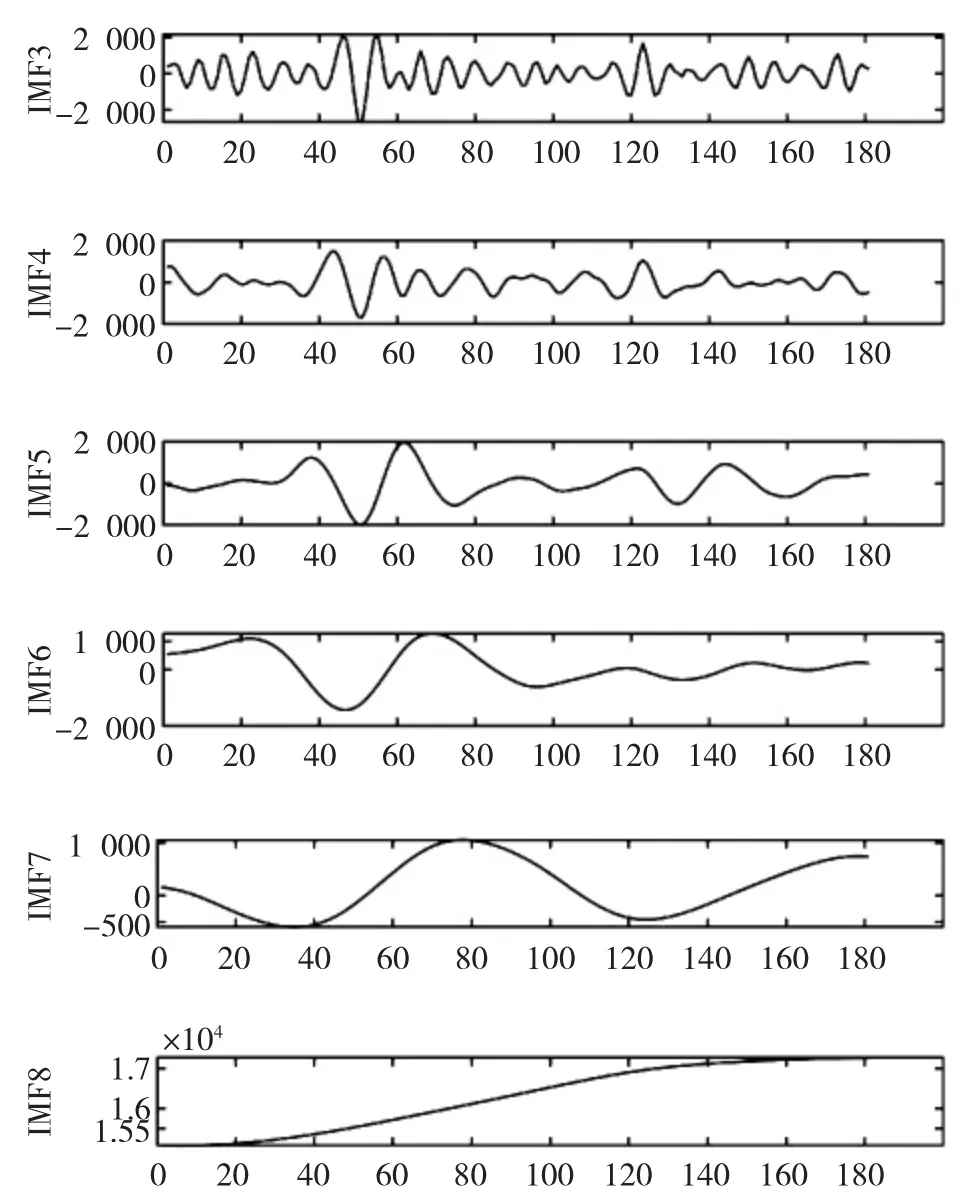
图1 CEEMD分解结果

图2 VMD分解结果

其中，原始数据经分解后,有针对性的将CEEMD分解结果输入ELM模型来预测和将VMD分解结果输入KELM模型来预测。同时,神经网络输入结构的设置也很关键，本文通过对比输入层节点数从3到10时的预测表现如图3所示，得出当节点数为7时可取得最好的预测效果。

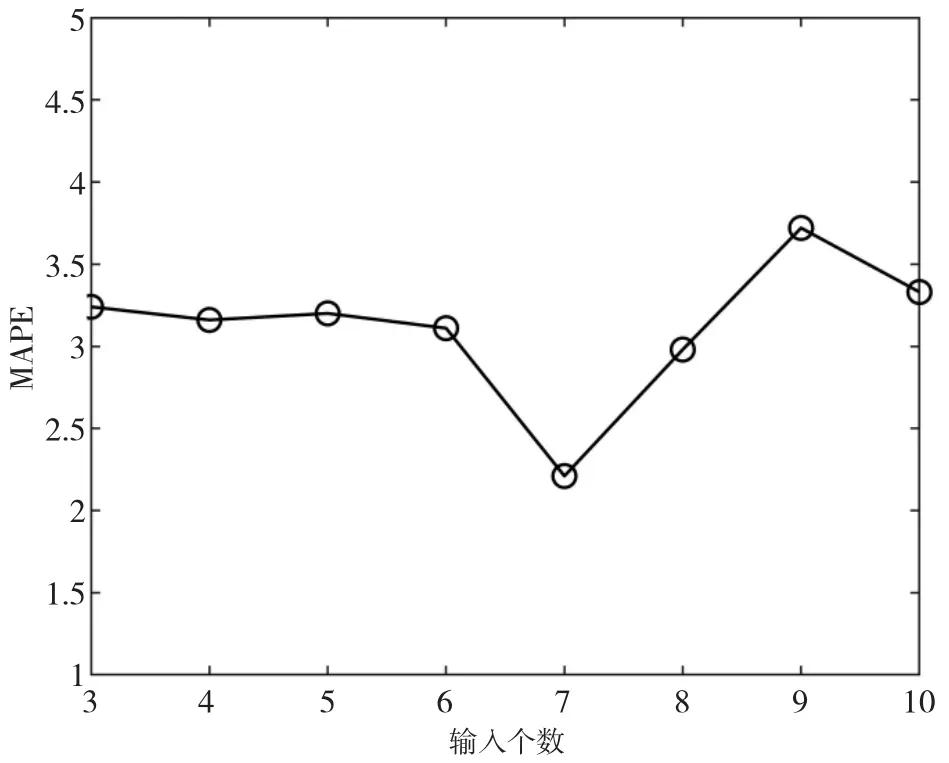
图3 不同输入个数预测结果MAPE值

3.3 预测结果分析

为了验证CEEMD-ELM-VMD-KELM模型预测的精确性，进行相关对比实验，其中不同模型的预测结果见表4和图4，通过分析得出：

图4 模型预测结果对比

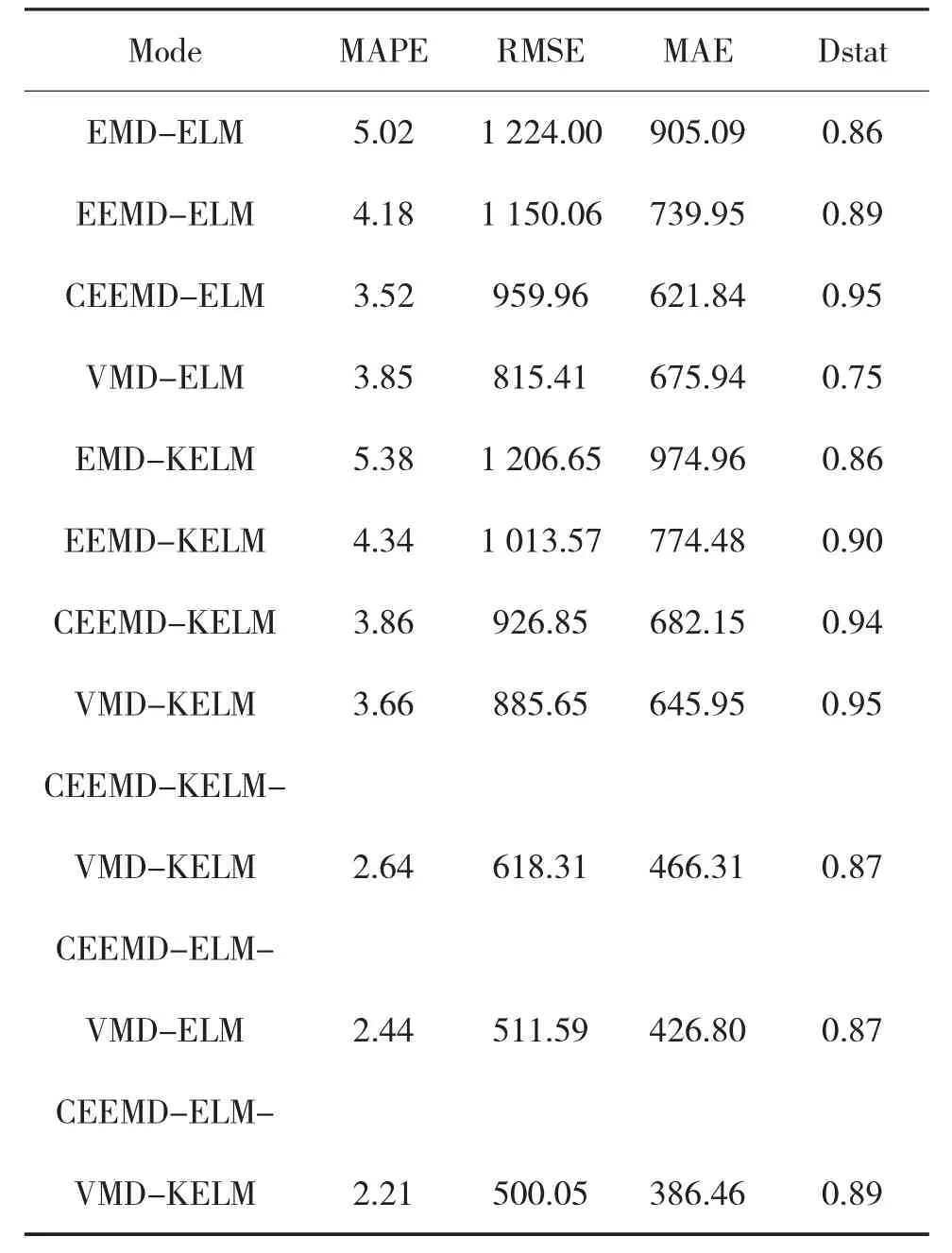
表4 各分解组合预测模型的评估结果

（1）在所有的一次分解组合预测模型中，CEEMDELM的平均绝对百分比误差值最低，均方根误差偏小，且其他两项指标都具有优势。同理在各指标下，VMD-KELM的预测效果也较好。这决定了后续的二次分解将分别采用完全重组经验模态和变分模态分解算法。当平均绝对百分比误差（MAPE）的值小于10的时候，预测结果良好[16]。

（2）相比较一次分解组合预测模型中最小MAPE值3.52，CEEMD-ELM-VMD-KELM的MAPE 值2.21减少了37.2%，这说明了二次分解可以将隐藏在数据序列背后的规律信息更充分地挖掘，降低一次分解后高频部分的预测难度，使得预测效果有所提升，进一步证明了二次分解预测的优越性。

（3）在所有二次分解方法的比较中，本研究提出的新型二次分解组合预测模型的预测结果在各项指标上表现最好。

最后，通过分别对基准模型、一次分解和二次分解组合预测模型中预测表现最好的模型预测结果作图比较可更直观看到，CEEMD-ELM-VMDKELM的预测曲线与原始数据曲线基本重合，预测结果最好，能够有效地对高铁OD日客流量数据进行预测。

4 结语

本文采用二次分解组合预测模对高铁OD日客流量进行预测,这为客流预测问题提供了全新的解决方法。具体在数据实验中进行CEEMD-ELMVMD-KELM模型构建,同时通过学习和训练,完成模型的最终预测。比较其他预测模型,结果显示本文中所构建的模型在预测精确度和稳定性上都有较大优势。仍要说明的是虽然在实例中的客流量预测虽然取得了良好的预测结果，但还需进一步优化模型以提高预测精度，且本文在后续研究还会充分考虑其他外在因素对预测精度的影响。