轮足复合机器人腿机构设计及仿真

詹玉新，乔英娜，张玉华

（1.滁州职业技术学院电气工程学院，安徽滁州 239000；2.库卡机器人(上海)有限公司，上海 200000；3.安徽工业大学机械工程学院，安徽马鞍山 243002）

根据机器人腿部的运动方式，可将机器人划分为轮式、足式以及轮足复合式机器人.轮式机器人机械结构简单、运动速度较快、能耗低、控制也相对比较容易，在平坦的地面上有不可替代的优越性，但是在山地和多障碍地面情况下轮式机器人很难适应.足式机器人却有着良好的机动性和对环境的适应性，能够在足尖点可达到的范围内灵活调整行走姿势，且具有更高的避障和越障能力[1-3]，但足式机器人却存在速度低、效率低的缺点.轮足复合式机器人则吸取了二者的优点，规避了二者的缺点，可以保持较快的行进速度，跨越更大的障碍，且更容易实现某些越障功能，有着更广泛的应用前景.例如在危险环境下取代人类的工作，在工业设备的维护、不平整地面的货物搬运以及灾害救助等方面能够发挥重要作用，其技术已经成为了移动机器人技术一个新的研究热点[4-6].例如北京理工大学研究的“北理哪吒”的轮足复合机器人，其总功率15 W，最大能承载300 kg，速度最高可达30 km/h，爬坡角度最高可达25°；瑞士苏黎世联邦理工学院研究人员研发的ANYmal四足轮腿式机器人，可以完成上楼梯，通过室内不同形状障碍物的功能，且实现±2 m/s速度的快速切换.

本文以液压马达为动力元件直接驱动各关节，设计一款四足轮足复合机器人腿机构，应用在机器人上.该腿机构结构简单，运动灵活，小腿和车轮通过离合器切换工作，实现足式方式下小腿的迈步运动和轮式方式下车轮的转动前进运动，且能更好地应对陌生和具有挑战性的环境.

1 腿机构方案设计

1.1 腿机构原理分析

所设计机器人腿结构以足式机器人为基础，在其基础上加入车轮部件.选用关节式腿机构，有三个转动副铰链，各腿部连杆通过铰链相互连接，足末端可以自由活动.根据机器人自身的体积、应用场合以及保证单腿结构运动的灵活性，及单腿重量尽可能小，故选用液压马达驱动，并将其置于髋关节及机体部分.腿机构原理如图1所示.

图1 单腿机构原理图

单腿为三关节串联机构，由于受自身机械结构的限制，其运动被限定在一定范围内.每条腿由两个液压马达、大腿、小腿、车轮和三个关节构成.三个关节均为转动副3R结构，每个转动副有一个驱动.车轮布置于大腿与小腿的连接处，即膝关节处.大腿轴线、小腿轴线及车轮中心位于同一平面内，构成单腿平面.根关节有一个绕垂直轴的转动自由度，可使整个单腿平面绕着垂直轴旋转，实现机器人直接转弯.髋关节和膝关节也各有一个自由度，可绕着各自轴线转动，实现机器人的俯仰运动.两个液压马达作为驱动源，通过控制马达的正转、反转，实现腿和轮子的正转、反转，从而完成整个运动过程.液压马达1输出的转矩通过齿轮传动传递给大腿，实现大腿的抬起与落下.液压马达2输出的转矩通过链传动传递给小腿和车轮，小腿和车轮通过离合器切换工作，实现足式方式下小腿的迈步运动和轮式方式下车轮的转动前进运动.因此，单腿机构在上端固定的情况下有三个自由度.

1.2 单腿机构方案设计

车轮采用车轮与轮毂一体的设计，链轮套在轮毂上，链轮传递的转矩推动轮毂转动，以带动车轮的转动，其单腿机构方案图如图2所示.

图2 单腿机构方案图

车轮布置于大腿与小腿的连接处，即膝关节处，采用离合装置来实现轮式运动与足式运动的切换.采用轮式方式行驶时，大腿与小腿挂靠在一特定位置，由链传动驱动车轮转动；当采用足式方式行驶时，通过链传动驱动小腿摆动，实现小腿的迈步.扇形齿轮圆心角为135°，髋关节可以在-30°～105°范围内转动，使大腿抬到一定的高度，以满足轮式或者足式运动状态下跨越障碍或者越过壕沟的功能要求；膝关节全角度转动时小腿可绕膝关节旋转整周，支撑机体抬高到一定的高度.

2 腿机构运动分析

2.1 正运动学分析

机器人在足式行走模式过程中，处于摆动相的各腿相当于机械手臂，是一个串联开链结构，即由根关节、髋关节、膝关节三条腿节构成.而位于支撑状态的立足腿与机体又构成了并联多闭链多自由度机构.因此通过计算各腿连杆之间相对运动与位姿关系，从而得出各腿部关节摆角与足末端点的关系[7].

利用“D-H”法则在机器人腿部各关节建立坐标系，其单腿“D-H”坐标如图3所示.

从图3知，在根关节、髋关节、膝关节和足端点处分别建立了四个坐标系.其原点为各关节轴线与相邻关节间公垂线的交点，分别为(X0Y0Z0)，(X1Y1Z1)，(X2Y2Z2)，(X3Y3Z3)，其中X0Y0Z0坐标系为定坐标系.图中θ1、θ2、θ3分别表示根关节、髋关节、膝关节的摆角，其范围分别为[-45°，105°]、[-30°，105°]、[0，360°].l1、l2、l3分别为各腿部连杆的长度，λ为基节两关节之间的夹角，其中λ=45°.相应的“DH”参数如表1所示.

图3 单腿“D-H”坐标图

表1 单腿“D-H”参数表

用Ai-1,i表示相邻两个关节之间的坐标齐次变换矩阵，并将各变换矩阵相乘得出一个总的变换矩阵，由此变换矩阵即可求解出各关节转角与足端的位姿关系.变换矩阵的通式如式（1）：

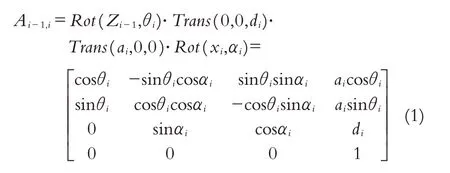
通过表1数据以及相邻关节齐次坐标变换矩阵，求得坐标系{0}与{1}、{1}与{2}、{2}与{3}之间的坐标变换矩阵如下：

所以足端坐标系相对于根坐标系的总变换矩阵为：

则有式（6）：

其中sθi=sinθi，cθi=cosθi，s(θi+θj)=sin(θi+θj)，c(θi+θj)=cos(θi+θj).

T是机器人的位置与姿态矩阵，则足端坐标系相对于根坐标系的变换矩阵为：

2.2 足端工作区域分析

机器人足端工作区域大小表明了机器人运动范围，是机器人在运动中的一个重要参数，为单腿摆动过程中足末端点相对于根坐标系原点在空间范围所能达到点的区域集合.

由于机器人四条腿构造相同且对称分布，所以只讨论其中一条腿的足端运动空间即可，并设定机器人基本参数为l1=353，l2=600，l3=400，R=207.

由机器人运动学正解，足末端点在根坐标系中的位置坐标，可根据公式(8)-(10)求得，采用蒙特卡洛法[8]利用三维绘图函数plot3绘制出复合机器人腿机构的足端空间（如图4）.

图4中X、Y、Z分别表示足端在机器人的前进方向、腿抬起方向和侧摆方向，可见机器人足端在摆角范围内符合实际运动，其工作空间范围大，运动灵活满足机器人的工作需要.

图4 足端工作空间图

3 腿摆动轨迹及步态规划

轮足复合机器人的运动是通过腿、轮或者腿与轮相结合的连贯动作实现的.当轮式与足式运动相结合时，控制会变得异常复杂，因此，需把腿部的运动形式确定下来，并对其步态运动进行细致的研究和合理的规划.

3.1 足端摆动轨迹

轮足复合移动对环境的适应主要是通过足式运动来体现的，对足端的运动轨迹进行规划，需考虑以下几点：

(1)足端点运动曲线的高宽比；

(2)足端运动曲线的弧长；

(3)足端轨迹曲线长度计算难度及其表达式的复杂性；

(4)不同路面对足端运动曲线的要求.

机器人的腿在XOY平面内摆动.X轴方向表示机器人运动方向，Y轴方向为腿抬起的方向.设单腿从抬起到放下所需的时间为t0，腿抬起高度为h，单腿步幅为E.由抬腿运动可知，X轴方向位移一直增大，Y轴方向位移增至最大值之后再减小为0，为了使运动平稳，选择匀变速运动作为足端的运动，因此可规划足端的运动规律如下：

X轴方向，t02时间匀加速运动，t02时间匀减速运动，完成单腿的迈步过程.

Y轴方向，t04时间匀加速运动，t04时间匀减速运动，腿抬至最高点；然后反方向，t04时间匀加速运动，t04时间匀减速运动，完成整个落地过程.

设计单腿的速度曲线为：

设定单腿步幅E=300，t0=1s，h=300，用MATLAB得到足端轨迹如图5所示.可见此轨迹较为光滑，在运动过程中不会有较大的突变，可以跨过较小的障碍物，可行性较好.

图5 足端轨迹图

3.2 步态规划

四足轮足复合机器人在足式运动状态下，其运动模式用“步态”表示，步态是指各腿之间具有固定相位关系的行走模式，常见的包括：行进步态，小跑步态和溜蹄步态[9].行进步态是一种运动较慢的步态，其四足在每一步行走中，必有三足支撑整个机体，稳定性较高.小跑步态是指处于对角线位置的两腿同时摆动，即左后腿和右前腿与右后腿和左前腿交替完成摆动和支撑运动.溜蹄步态是指同侧的两条腿（即左后腿与左前腿或右后腿与右前腿）同时摆动和支撑.

生活污水采用化粪池处理后排入附近污水坑中，建设地理式一体化生活污水处理设施，处理后的污水要满足《污水综合排放标准》的规定要求，或排入城市管网进行处理。固体废物在厂区垃圾箱中集中堆存，定期由环卫部门外运处置。锅炉灰渣外运用于制砖或筑路等。

衡量一种步态好坏的因素主要在于，在一定的稳定裕度条件下，步行速度越快，消耗的能量越少，此种步态就更为优越.将右前腿编号为1，按逆时针旋转各腿编号为2、3、4.根据相关研究结果综合各方面的因素，选择1→4→2→3步态，即按照腿1、腿4、腿2、腿3的顺序依次抬起和放下（如图6）.

图6 机器人腿编号图

本文采用重心随动调整的前进步态规划，即在迈腿的同时进行机体重心的调整，这是以牺牲稳定裕度为代价的，但改善了重心单独调整的静态步态规划中机体运动不连续、速度变化大的缺点.根据采用的重心随动调整前进步态，设定机器人各腿迈动与机体前进关系为：

(1)迈1腿，机体前移m/4，t=1s；

(2)迈4腿，机体前移m/4，t=2s；

(3)迈2腿，机体前移m/4，t=3s；

(4)迈3腿，机体前移m/4，t=4s，回到初始状态.

4 仿真分析

利用ADAMS[10]建立轮足复合机器人虚拟样机模型，并添加所需的约束和驱动，对相关构件进行运动学分析，为物理样机的设计与制造提供参数依据.图7为添加约束和运动后的虚拟样机模型.

4.1 足端运动轨迹模拟

一方面可以模拟在主动关节驱动情况下，末端执行器的运动；另一方面可以按照实际操作要求规划末端执行器的运动，仿真模拟机构主动关节的运动.

根据规划的足端抛物线轨迹，取其中20个点，并用STEP函数将其轨迹拟合出来，编辑如下的运动规律：

跟踪足端点的运动轨迹为抛物线形式（如图8所示），符合理论规划的足端轨迹.

图8 足端点运动轨迹图

4.2 足式重心随动模式运动仿真

与重心随动模式相比，机体在腿移动的同时向前移动，运动过程连续，机体与腿机构没有较大的冲击，比较符合实际情况，但同时稳定性稍差.机器人躯体位移、速度加速度曲线图如图9-10所示.

图9 机器人躯体位移曲线图

从图9躯体位移曲线图可知：机器人在运动过程中，躯体在Y和Z方向没有位移，一直沿着X方向即前进方向运动，0～4 s内机器人躯体前进300 mm.曲线比较光滑，表明机器人在规划的步态及运动模式下能够平稳运动.

从图10机器人躯体速度和加速度曲线图可知，在（0～4）s机器人各腿摆动过程中，其躯体质心速度和加速度均匀增加和减少，不发生突变，运动平稳，符合其轨迹参数运动规律.

图10 机器人躯体速度、加速度曲线图

4.3 轮式爬坡模式运动仿真

在轮式爬坡运动模式下，设置斜坡角度为30°，车轮所添加的运动参数为-150 d★time，运行时间为前6 s，其躯体质心位移、速度及加速度曲线如图11-13所示.

图11 轮式机器人运动躯体位移曲线图

由图11可以看到，机体质心X方向的位移一直增大，但从5 s开始有下降的趋势，可以知道驱动力不足以使机器人爬上斜坡，使机器人产生后退现象，需要合理调整其速度大小.Y方向位移随着1 s爬坡运动的开始增大，同X方向位移，车子产生后退.Z方向位移没有变化，说明机器人一直处于直线运动状态，没有偏移.

从图12可知，机器人在开始运动时，速度增加较快，之后波动趋于平稳，在后轮上坡时，速度下降，并出现后退现象.

图12 轮式机器人运动躯体速度曲线图

从图13可知，加速度变化在前轮上坡时比较大，后轮上坡瞬间同前轮上坡时变化相差不大，在车体后退的瞬间加速度迅速增大，使速度和位移发生变化.

图13 轮式机器人运动躯加速度曲线图

5 结语

本文综合足式与轮式优点，设计一款轮足复合机器人腿机构，并应用在四足机器人上，进行正运动学分析，得出足端工作空间.在确定足端摆动轨迹及四足步态规划基础上，建立轮足复合机器人虚拟样机模型，在足式重心随动和爬坡模式上分别对其进行足式和轮式运动模式分析，分析结果证明了理论设计的正确性，可为后期的深入研究提供基础.