高放废物处置库缓冲层热-水-力耦合数值模拟

王玉平，王 哲，易发成，曾志强

（1.宜宾学院国际应用技术学部，四川宜宾 644000；2.西南科技大学环境与资源学院，四川绵阳 621010；3.宜宾学院理学部，四川宜宾 644000）

核能的高效利用和核武器的发展，产生对生物圈有害的放射性废物.特别是高水平放射性废物（简称高放废物,HLW），是对环境潜在危险最大的放射性废物，其放射周期可达上万年，是最难处置且最受关注的科学问题，到2050年，我国将产生8.3万吨乏燃料[1].目前世界上主要有两种处理方式：一是通过核嬗变法改变核素性质使之无毒化；二是深地质处置使之与生态圈完全隔离.深地质处置，是将HLW采用工程屏障系统和自然屏障系统深埋于地下500-1000米，使核废物与生物圈永远隔离.在HLW深地质处置的工程屏障体系中，缓冲材料一方面延滞废物中核素向地下水迁移，另一方面阻止核素进入生物圈环境.对于HLW处置中热-水-应力（THM）耦合过程的研究，许多学者从试验和理论方面做了很多工作，包括室内试验、原位试验和数值模拟.因多场耦合试验周期长、相互作用复杂，因此更多的是建立理论模型进行研究.

Biot[2]最先提出了流体饱和多孔介质的动力学问题，并推导了基本控制方程，在水文学、土力学等领域发挥了重要作用.Noorishad等[3]在Biot固结理论的基础上推出饱和土体的THM耦合方程，Barton和Bandisoo[4]对考虑地下水的工程中应力场、渗流场以及温度场之间的耦合关系做了更深一步的研究.1990年，Mu和Landanyi[5]首次提出THM三场耦合问题，并给出了简化的模型，耦合问题开始成为研究的重点.国内外大多数多场耦合模型都是在连续介质理论基础上建立的.Zhang等[6]对深地质处置库中的Callovo和Opalinus黏土的THM行为进行了广泛的研究，Yu等[7]研究了HLW释放热量导致孔隙压力增加.Collin[8]提出一个THM模型解决粘土屏障中的耦合问题，并对压实膨润土进行湿热试验对比验证.Kanno[9]对地质处置库中缓冲材料的THM耦合过程进行了力学模型开发和数值模拟.Della[10]对压实粘土的持水和应力应变，提出了一种考虑土体多相多尺度耦合的本构模型.Fernandez[11]通过试验研究不同温度对高压实膨润土渗透系数的影响.

本文以混合物理论为基础，基于COMSOL有限元分析平台建立轴对称模型，对Mock-up试验台架中缓冲层的THM耦合进行有限元模拟，考察缓冲层中温度场、饱和度和应力场的分布及变化规律，以期为高放废物处置库设计提供依据.

1 非饱和缓冲材料THM耦合模型

连续介质理论认为，在物质所占据的空间中，物质是无间隙地连续分布的.可忽略物质的微观结构，用偏微分方程表达宏观物理量.混合物理论是在现代连续体物理的精神下发展起来的，提出了一个新的构成公理“成分的等同性”，并用它来获得与微观对应相一致的宏观构成方程.混合理论用于将连续介质力学原理推广到几个可相互渗透的连续介质来模拟多相系统.为构建弹性力学基础上的多孔介质THM耦合模型，作如下假设：

（1）非饱和的介质被视为多相系统(固体、液体和气体).孔隙一部分被液态水填充，一部分被气体填充.

（2）多相介质是一种混合物，每一相都是连续的，每个空间点同时被一个物质点占据.

（3）气相密度是温度和压力的函数，且满足理想气体状态方程.

（4）流体渗流符合Darcy定律，且流体不与固体颗粒发生化学反应.饱和蒸气压力满足Kelvin湿度定律，水蒸气的扩散符合广义Fick定律.

（5）多孔介质的变形满足小变形假设，Terzaghi有效应力原理对非饱和介质适用.

（6）假定固、液、气三相保持局部热平衡.

多场耦合的场与场之间是密切相关的，物理场变量与其它物理场变量之间是相互影响的.高放废物处置库中的缓冲材料作为一种多孔介质，满足多场耦合作用的理论体系，包括连续介质理论、混合物理论、渗流力学、传热学理论、普遍的守恒原理及Fick定律等.为了建立非饱和缓冲材料THM多场耦合数学模型，需结合混合物理论、连续介质理论、三大守恒定理（动量守恒、质量守恒、能量守恒）以及Fick定律推导非饱和缓冲材料的THM耦合控制方程.

1.1 动量守恒方程

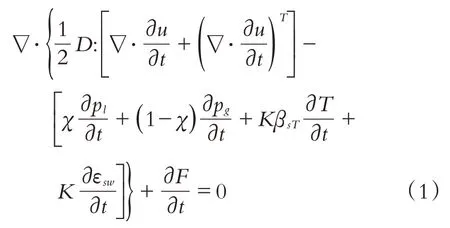
式中：D是弹性张量，u为位移向量，T为温度，χ是Bishop系数，Pl是液体压力，Pg是气体压力，K是土体的排水体积模量，βsT是固相体积热膨胀系数，εsw是土体湿化膨胀体积应变，δ是Kronecke单位张量，F为体积力.

1.2 质量守恒方程

（1）固相骨架质量守恒方程

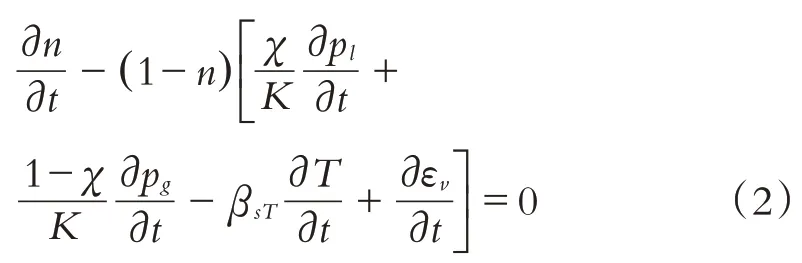
式中：n为孔隙率，εv为土体的体应变，孔隙水压为pl，孔隙气压为pg.

（2）水体质量守恒方程

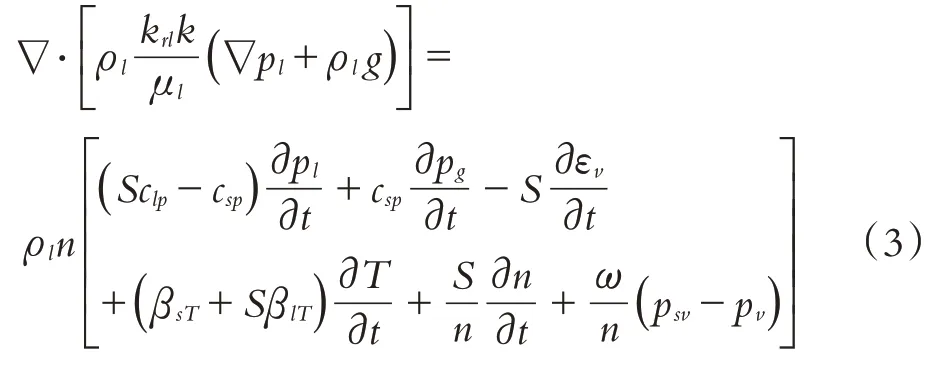
式中：ρl为水体的密度，k是本征渗透率张量，krl为水体的相对渗透率，μl是水的动力黏滞系数，pl为液体压力，S为饱和度，clp为压缩性系数，csp为饱和度的吸力影响系数，βsT为饱和度的温度影响系数，βlT是热膨胀系数，ω为液相迁移系数，psv为饱和蒸汽压力，pv为蒸汽压力.

（3）气体质量守恒方程

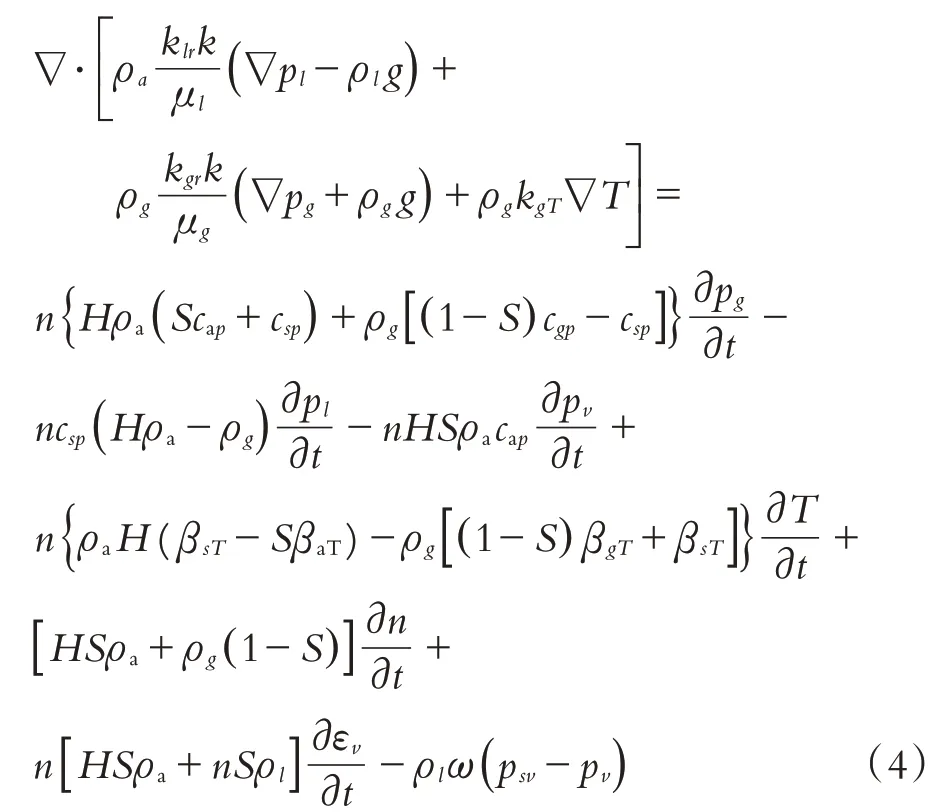
式中：vgr为气相相对于固相的本征流速，klr为液相相对渗透率，kgr为气相相对渗透率，kgT为混合气体热驱动系数，μg为气体的动力粘滞系数，ρg为混合气体的本征密度，cgp为压缩系数，βgT为混合气体热膨胀系数，cap是干空气压缩系数，βaT是干空气热膨胀系数，H为Henry溶解系数，ρl、ρa分别为水、干空气的密度.

1.3 能量守恒方程

给定任意单元体，在单位时间内α相总内能的变化率是一定等于该相穿过单元体的热流量加上热源，三相混合的能量守恒方程可以写为：

式中：vgr为气相相对于固相的本征流速，kgr为气相的相对渗透卒，kgT为混合气体热驱动系数，μg为气体的动力粘滞系数，Ks、Kl和Kg分别为固、液和气相体积应变模量，βs、βl和βg分别为固、液和气相体积热膨胀系数，cs、cl和cg分别为固、液和气相比热容，λ为热传导系数.

2 高放废物处置概念库及耦合模型参数

2.1 高放废物处置概念库

本文的多场耦合缓冲材料长期阻滞性能Mock-up试验腔体直径750 mm，高750 mm，内部加热器高180 mm，外径200 mm；罐体为密封状态，内部的空气、水蒸气不与外界交换，故气体边界均设为零通量边界.基于COMSOL多场耦合问题的计算模块，试验台架的数值计算模型如图1所示.取沿加热器边缘中点水平方向为截面A，图1（c）为截面A上11个计算结果输出点的位置，其中A点（x=0.09 m）位于加热器外缘中部，B点（x=0.23 m）位于缓冲层中间，C点（x=0.37 m）位于靠近围岩的缓冲层.COMSOL中理查兹方程接口可用于描述变饱和多孔介质流体运动，理查兹方程模型中饱和液体体积分数设定为1，残余液体体积分数设为0，渗透率模型选择“渗透率”，储水模型选择“用户定义”，保留模型选择Van Genuchten(VG模型)，VG模型的参数分别为a=0.009，b=1.3386，l=2.46×106J/kg.

图1 试验台架的数值计算模型

2.2 缓冲材料的相关参数和本构方程

缓冲材料力学模型为线弹性模型，其性质参数如表1所示.

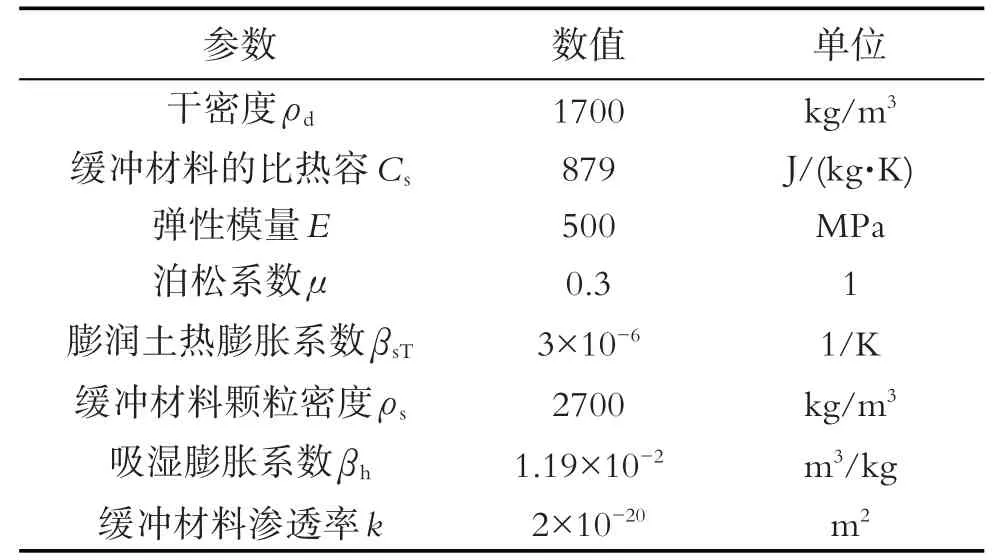
表1 膨润土性质参数[12-14]

本构关系如下：

（1）膨润土的水体热驱动[15]系数：klT=2.5×10(n×S-15.5).

（2）通过试验得到膨润土的导热系数：λ=2.1545ω+1.0316ρd-1.9875n+0.6181S-0.5508.

2.3 流体的相关参数和本构方程

采用的VG模型可使饱和土的吸力为0，符合吸湿过程中土的吸力变化特点[16]，相关参数见表2.

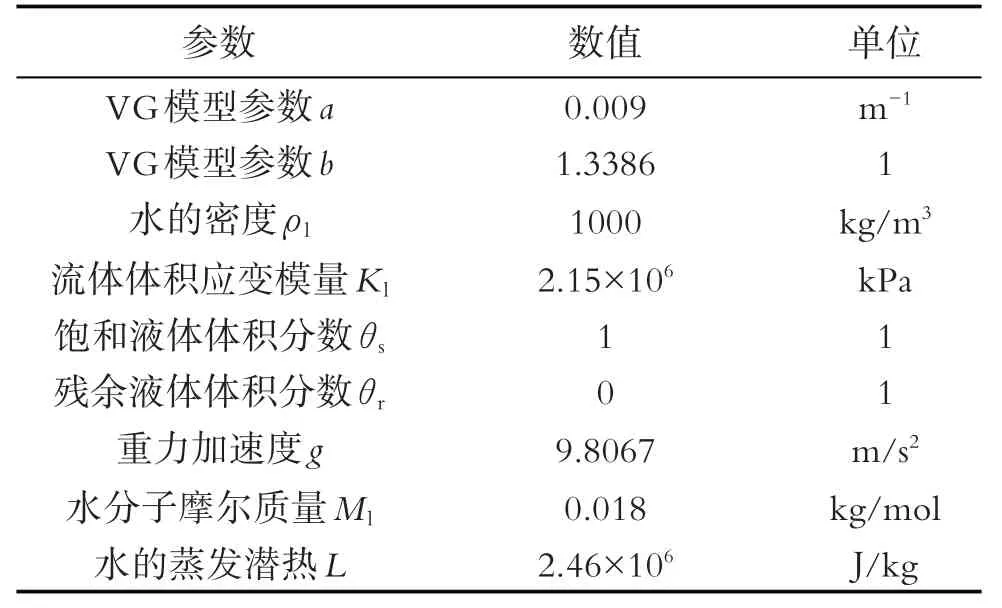
表2 流体的相关参数

流体的相关本构关系如下：

(1)水体相对渗透率[17]

其中n为孔隙率，n0为初始孔隙率.

(2)水 体 动 力 粘 滞 系 数[18]μl=1.984×10-6×

(3)水体的热膨胀系数[12]βl=1.7769×10-10T3-5.7556×10-8T2+1.1383×10-5T+3.024×10-6.

(4)水体的比热容Cl=6872.8945-23.09T+0.069T2-7.35×10-5T3.

(5)液相迁移系数[19]ω=其中C为调节系数，取2×10-5；R=8.3144 J/(mol·K).

2.4 气体的相关参数和本构方程

气体相关参数如表3所示.

表3 气体的相关参数[20,21]

气体的相关本构关系如下：

(1)气体密度.气体包含水蒸气和干空气，N2和O2组成干空气（体积比4∶1）.则水蒸气密度、空气密度和干空气密度分别为：

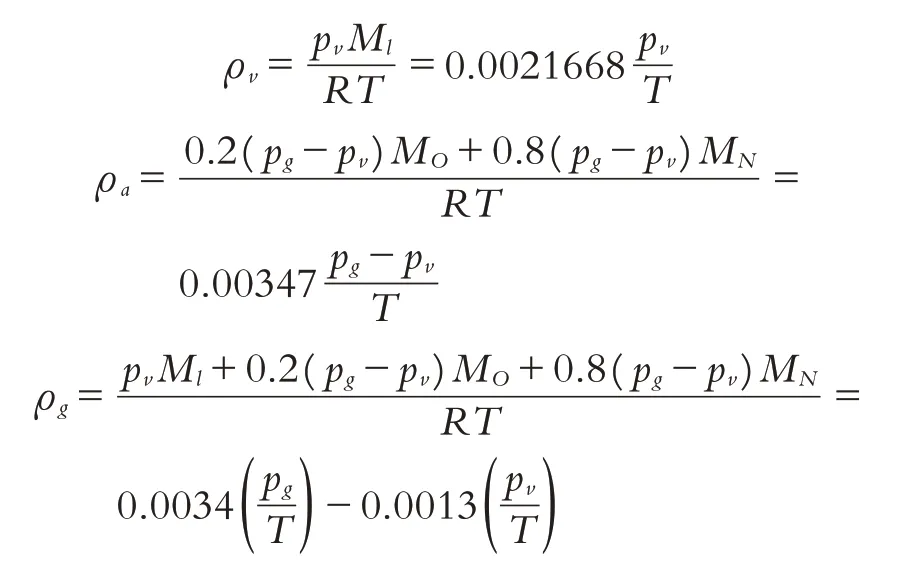
式中：Ml为水分子摩尔质量（0.018 kg/mol），pv为蒸汽压，MO为O2摩尔质量（0.032 kg/mol），MN为N2摩尔质量（0.028 kg/mol）.

(2)气体热驱动系数[12]：kgT=6×10-12(1-S).

(5)干空气溶解系数.干空气主要由氧和氮组成，Henry溶解系数H[12]可以表示为：

3 THM耦合数值模拟结果及分析

3.1 温度场变化过程

缓冲材料的温度场变化趋势如图2所示，可见缓冲材料的温度随时间不断升高.

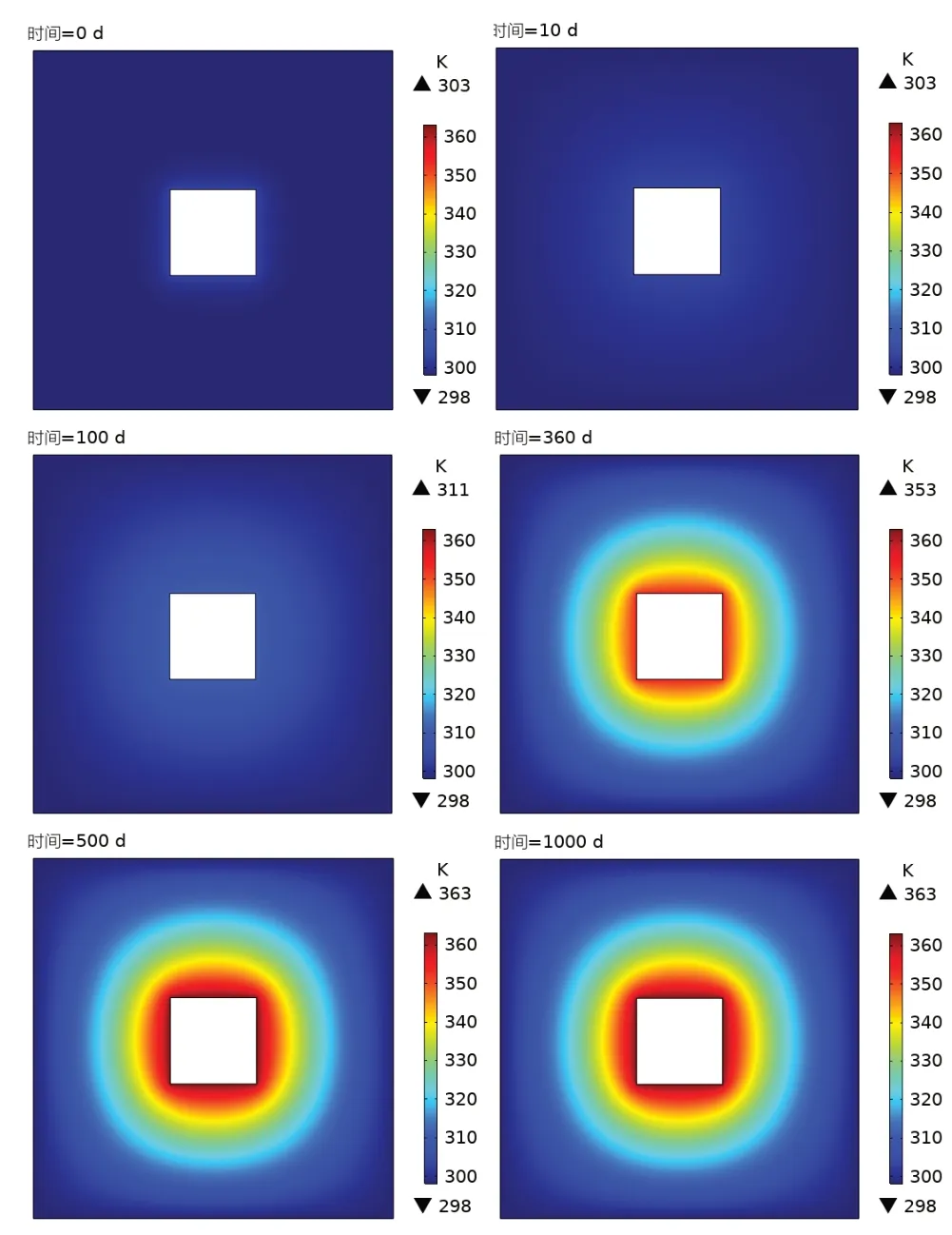
图2 缓冲材料温度场分布变化

第10天，缓冲材料温度变化不大；第100天，将加热器设定为30℃并保持恒定，并在缓冲材料外边界处施加0.1 MPa水头压力，随着热量向往扩散，加热器周围温度场已有明显小幅度上升，而缓冲层外边界温度场未发生明显变化.这是因为膨润土的渗透速率较慢，渗透系数较低.当试验进行到150天时，加热器升温到40℃，而缓冲材料外边界处水头压力约为0.5 MPa，缓冲材料由内向外温度梯度逐渐增大，加热器周围缓冲材料温度上升较快，缓冲材料外边界约为30℃，在351天时，将温度升到90℃并保持恒定，此时缓冲材料外边界处水头压力为1 MPa，相对于360天而言，1000天时加热器周围的缓冲材料温度场分布稳定，缓冲材料外边界温度值较低，且变化较小，因为水头压力加速了水的渗流，带走一部分热量.500天和1000天相比变化不大，说明在500天时，缓冲材料就可以把废物罐产生的热量传到HLW处置库外，防止处置库内部热量聚集，有利于HLW处置库的安全和稳定.

图3为温度随径向距离的变化趋势.距加热器越近，温度越高，温度从靠近加热器到外边界逐渐降低，呈线性分布.第10天缓冲层内温度保持在30℃，加热后第100天温度迅速上升.第1000天在靠近围岩的缓冲层处温度低于30℃，说明热传递和地下水渗透已经贯穿整个缓冲层.在500天和1 000天的温度分布变化很小，说明膨润土的导热性能较好，温度趋于稳定.图4显示了截面A不同位置的温度随时间的演变.可以看出：各点的温度都随时间的增加而增大，且距离加热器越近，曲线斜率越陡，温度增长速率越大.靠近加热器处的缓冲层，温度很快达到80℃，随后温度增速减缓趋于稳定.缓冲层中间的温度值很快达到50℃稳定下来，反映出缓冲层具有较好的热稳定性.

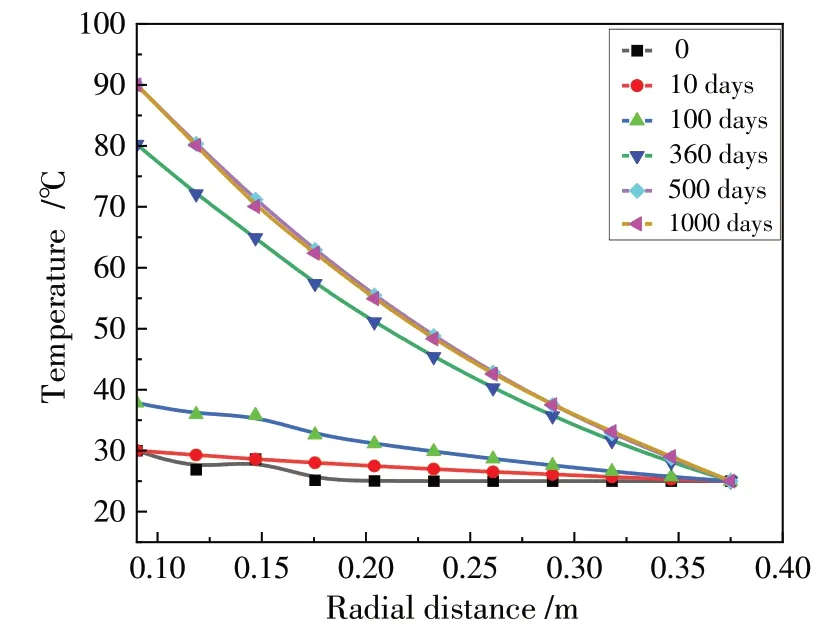
图3 温度随径向距离的变化

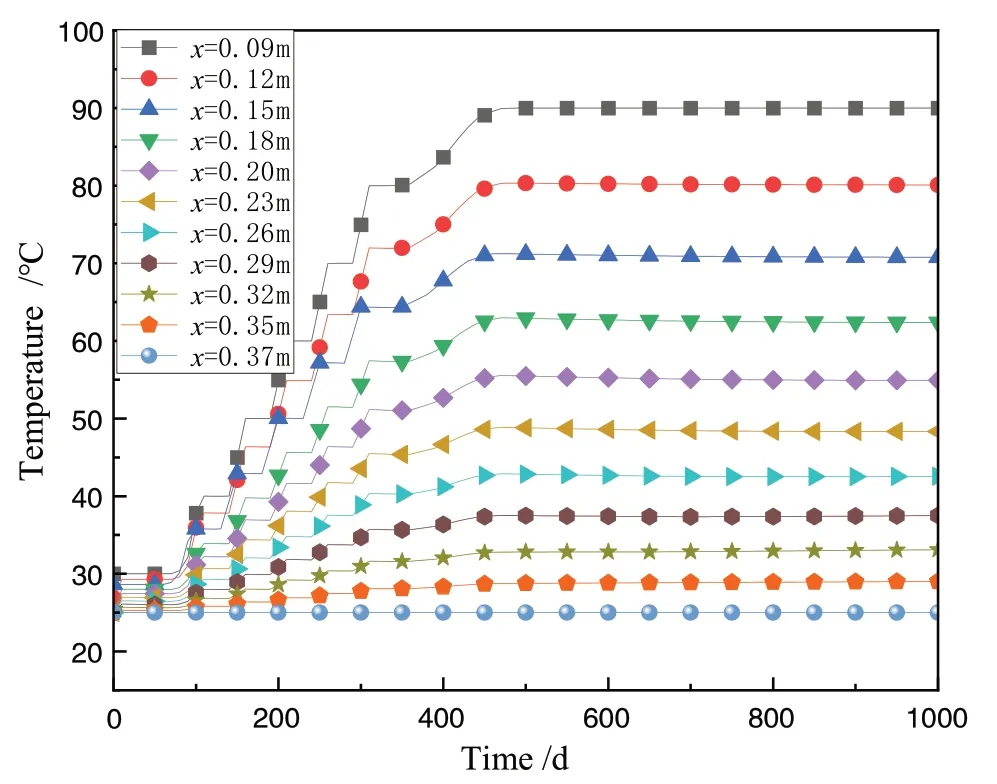
图4 温度随时间的变化

3.2 饱和度变化过程

图5 所示的缓冲材料的饱和度变化趋势表明，在水平方向上，饱和度值从外向内逐渐增大，在竖直方向变化规律一致，没有出现因为加水方式和水的重力作用，导致缓冲层上、下部含水量差异较大的情况.在竖直方向上出现饱和度值中间大，两头小的轻微差异，这是因为模型层上下水力边界条件为不透水边界，上下部分的水体只能向中间渗透.

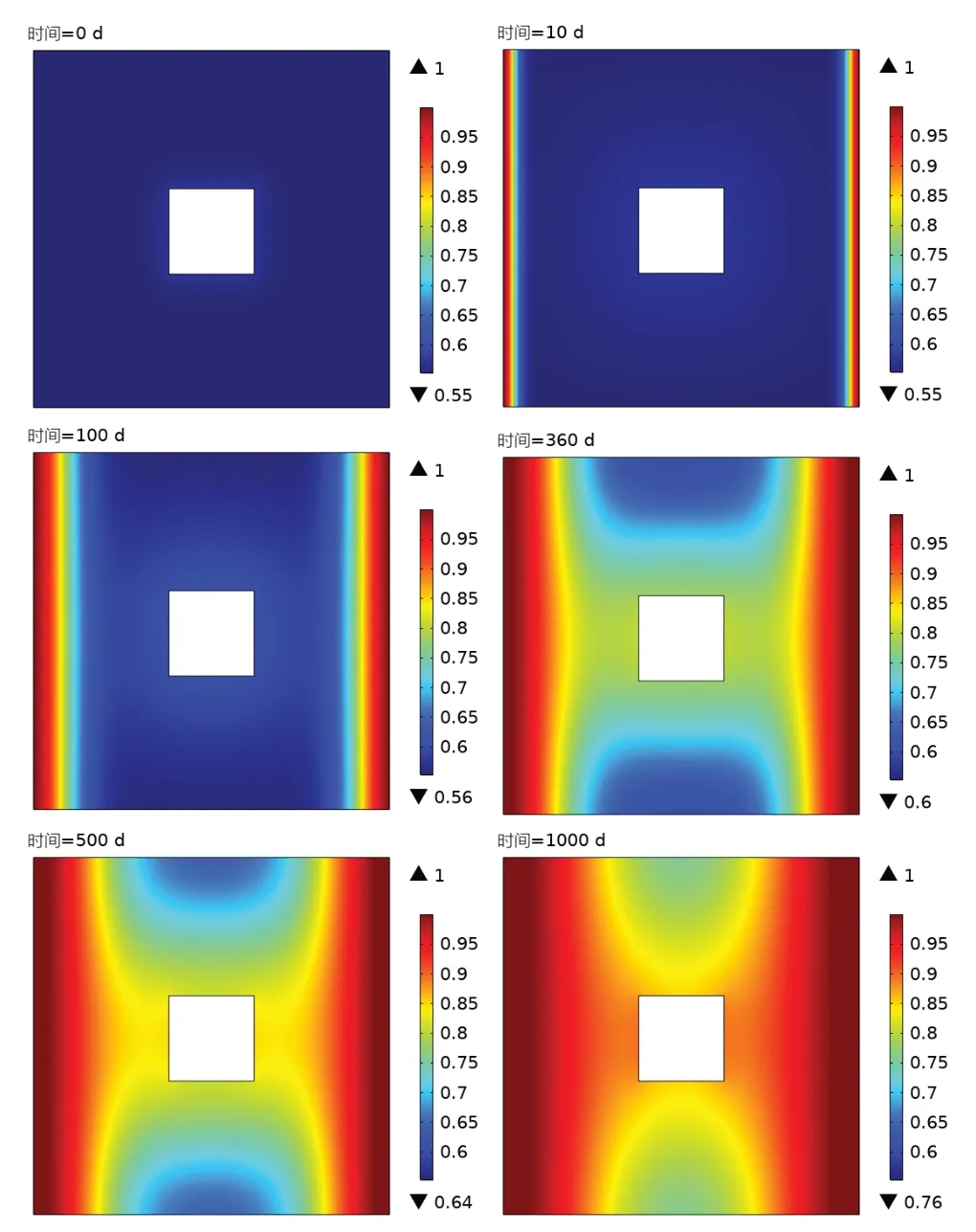
图5 缓冲层饱和度随时间变化

图6 显示了饱和度随径向距离的变化趋势，在试验前100天，靠近围岩的饱和度值迅速上升，靠近加热器的饱和度值有所下降，中间缓冲层变化很小；当试验进行到500天，靠近加热器一侧缓冲层饱和度值达到了85%；靠近围岩的缓冲层已经饱和；当试验进行到1000天，靠近加热器一侧饱和度值达到89%.随着试验的继续，整个缓冲层饱和度值分布逐渐趋于均匀.图7显示了截面A上饱和度值随时间的变化曲线，每个点的饱和度值都随时间的增加而增大，且距离注水边界越近，曲线斜率越陡，饱和度值增长速率越大；在加热器附近，其饱和度值先减小再达到稳定，随后缓慢上升.整个试验过程饱和度值以不同的增长速率进行，这可能是由于水沿着传感器电缆渗透和膨润土混合物的不均匀性造成的.靠近加热器到缓冲层一半的饱和度值，在试验前400天呈现波浪形态，这是因为模型考虑了水蒸气的蒸发和孔隙气压导致饱和度值暂时减小.A、B两点的饱和度值在开始阶段变化不大，分别为57.61%，55.35%，随后慢慢增大，大约在500天分别为84.78%，88.17%，这是因为在试验初期，加热器温度为30℃，靠近热源一侧缓冲层的温度迅速上升，湿度逐渐减小，热效应大于湿效应.随着高压水头作用，饱和度值升高，上升速度为前期慢后期快，而C点的饱和度很快上升到100%，因为该点受到地下水的充分渗透.

图6 饱和度随径向距离的变化

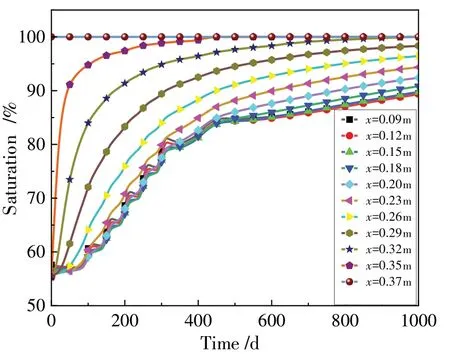
图7 饱和度随时间的变化

3.3 膨胀力变化过程

缓冲材料的膨胀力变化趋势如图8所示.试验初期，进水压力小，缓冲层渗透性较低，膨胀力增长缓慢.当应力传感器与缓冲材料砌块完全接触后，随着进水压力的增大，水力边界处的膨胀力快速增大，随后其他缓冲层的膨胀力也不同程度的增大.第0天，缓冲材料处于非饱和状态，整个缓冲层的膨胀力为负值；第360天，注水压力恒定为1 MPa，水力边界处缓冲层迅速膨胀，膨胀力增大；第500天，注水压力升到1.5 MPa并保持恒定值，加热器温度为90℃，缓冲层进一步向里渗透，膨胀力继续不断增大.第1000天，随着试验的继续，膨胀力由外向内逐渐变大并达到峰值.

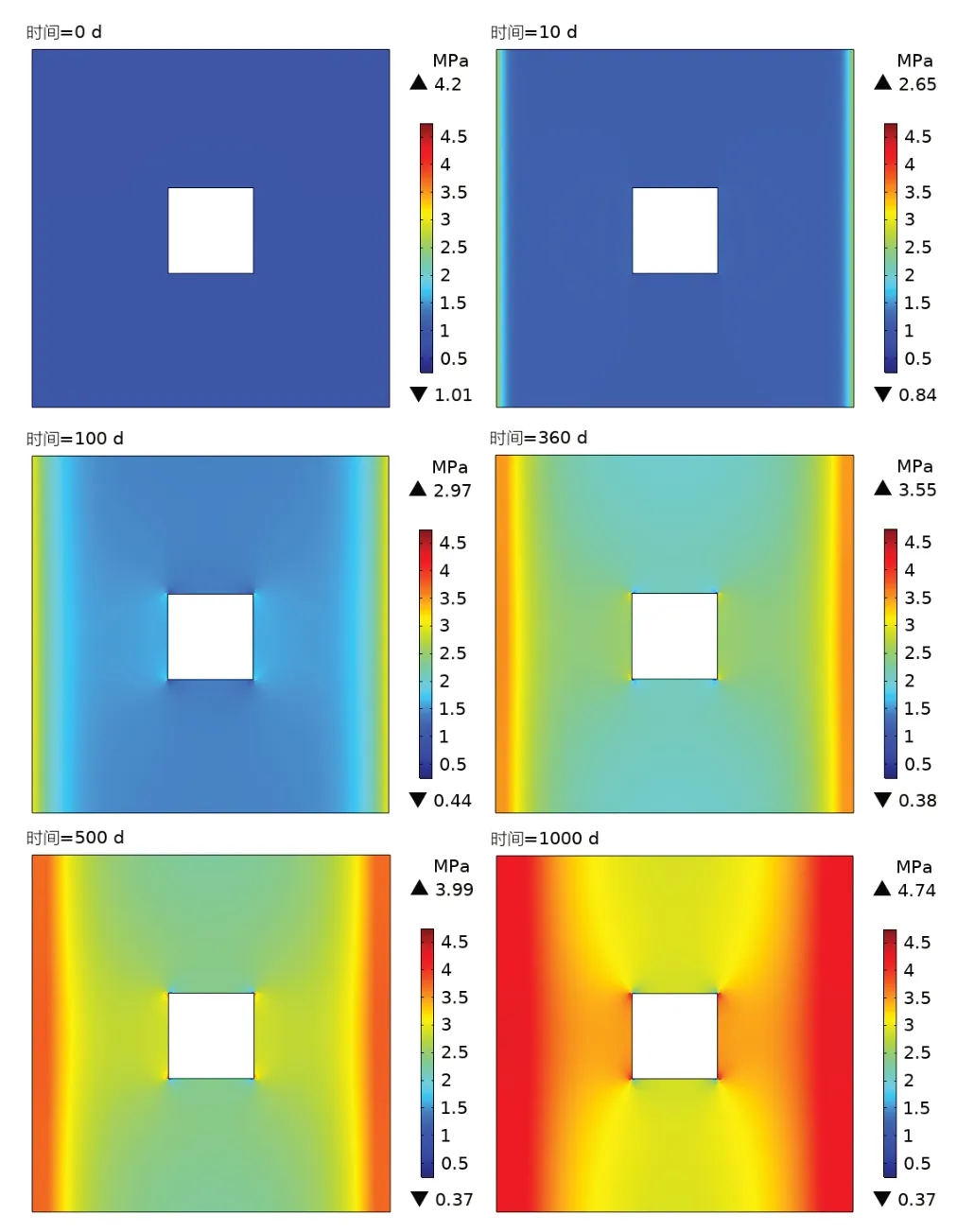
图8 缓冲层膨胀力随时间变化

图9 是膨胀力随径向距离的变化趋势，说明膨胀力从靠近围岩边界开始增大，在靠近加热器附近，由于温度升高导致膨胀力有所下降.

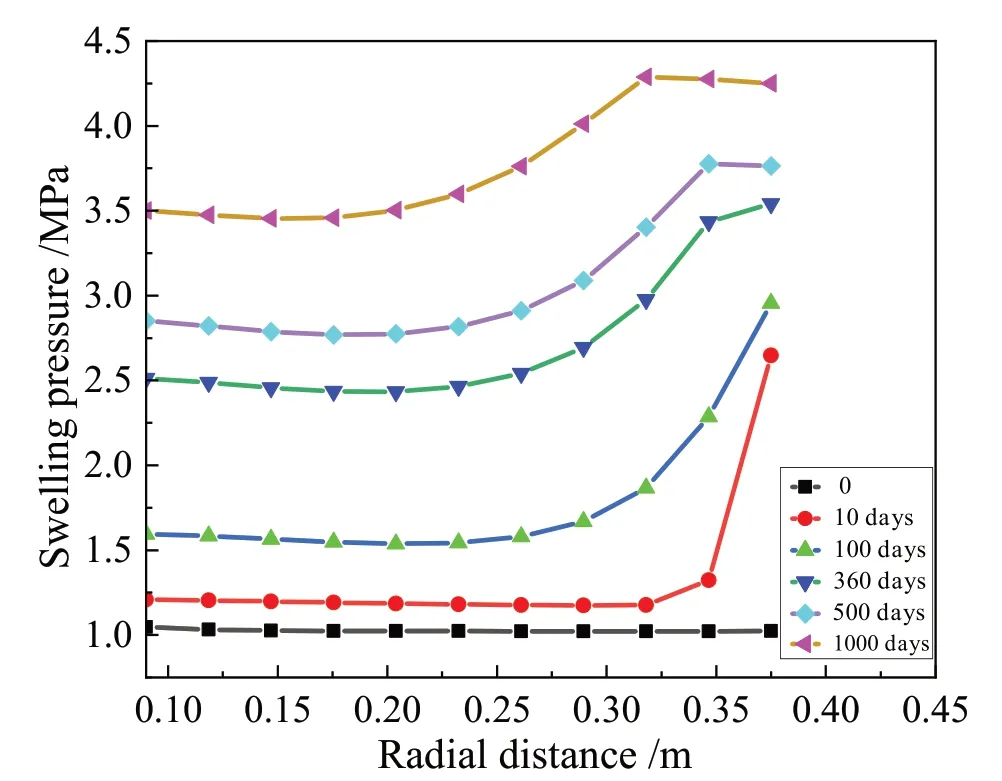
图9 膨胀力随径向距离的变化

图10 为截面A上各点膨胀力随时间的变化曲线.总的来看，每个点的膨胀力都随时间的增加而增大，膨胀力时程曲线经历了快速膨胀、缓慢膨胀并逐渐趋于稳定.距离注水边界越近，曲线斜率越陡，膨胀力增长速率越大；距离加热器越近，曲线斜率越缓，膨胀力增长速率越小.含水量从加热器向缓冲层逐渐下降，水分重新分布导致局部膨胀力增加.注水压力一直保持恒定的增长，由于不断向缓冲层注水，使得缓冲层的饱和度值不断升高，并在其周围形成孔隙压力，缓冲层的孔隙压力和饱和度不断重新分布调整，因此膨胀力曲线出现小波动变化.

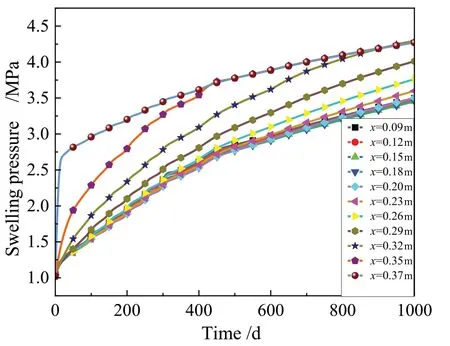
图10 膨胀力随时间的变化

4 结语

本文通过COMSOL有限元数值模拟，探讨了高放废物处置库缓冲层非饱和介质中的热-水-力多场耦合现象，（1）基于混合物理论，将缓冲材料视为多组分连续介质，针对耦合概念模型提出了基本假设，为建立数学模型提供理论依据和前提.考虑蒸发潜热的影响，基于质量守恒方程、能量守恒方程和动量守恒方程，建立了非饱和缓冲材料的THM耦合数学模型，得到关于水压、温度等数学物理方程.（2）发现缓冲层中温度随时间先增大后趋于稳定，且距离加热器越近，曲线斜率越陡，温度值增长速率越大，说明缓冲层具有良好的热传导性.温度对缓冲层饱和度的影响较大，特别是在靠近加热器周围，饱和度在水平方向上，从外向内逐渐增大，在竖直方向变化规律一致，没有出现因为加水方式和水的重力作用，使得下部水量增多的情况.缓冲层中膨胀力受到水压和温度的共同影响.试验初期，进水压力小，膨胀力不断调整，膨胀力增长缓慢.随着进水压力的增大，缓冲层的膨胀力不同程度的增大.靠近水力边界的缓冲层膨胀力受高压水头作用，膨胀力较大，本文建立的模型能够体现温度-渗流-膨胀力耦合现象，可为高放废物地质处置库设计提供依据.