地基大口径望远镜重力弯曲引起的指向变化检测与修正
2023-01-06王洪浩王建立曹玉岩陈宝刚
王洪浩,王建立,陈 涛,曹玉岩,陈宝刚
(1. 中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;2. 中国科学院大学,北京 100049)
1 引 言
随着口径的不断增大,望远镜的尺寸相应增加且结构越来越复杂,重力场变化引起的望远镜光轴指向变化影响也愈发明显,进而影响望远镜的跟踪精度,望远镜的指向变化检测与修正已成为研究的热点和难点[1]。
以中国科学院长春光机所4 m 望远镜为例,在跟踪过程中采用独立结构的捕获跟踪器进行闭环跟踪,装调过程中确认跟踪器的光轴与主次镜光学系统光轴的平行度是至关重要的。但是由于跟踪过程中望远镜俯仰角的变化和受到站址的限制,两者光轴并没有严格保持平行,引入跟踪误差,重力弯曲会导致图像运动,这是大型地基望远镜的普遍问题。在望远镜跟踪与指向误差修正方面,欧洲南方天文台ESO 在NTT 望远镜上提出了一种基于主动光学的校正技术[2],使用图像传感元件来观察望远镜跟踪与指向信息的变化,以此作为反馈来调节副镜的位置以校正跟踪与指向信息误差。该系统随后被应用于8~10 m 量级的巨型地基望远镜[3-7]。其中,VLT望远镜使用3 个单独的调节机制来逐一调节跟踪与指向信息的误差,TNG[4]和VST[8]使用副镜调节平台来弥补光轴的变化。Gemini 近红外光谱仪(GNIRS)使用单个敏感光学器件的可调节悬臂式铰链,在设计过程中对比重力影响,并通过驱动连接到准直器上的倾斜偏摆镜进行调整[9]。对于正在建设的NOAO 极宽视场红外马赛克相机(NEWFIRM),整个光学系统的支撑结构相对于望远镜焦平面的偏转和精确旋转可以进行机械调整,光学系统保持在焦平面的一个固定位置上,使科学探测器上的图像运动最小化[9]。
国内天文望远镜一般利用统计的方法建立望远镜的指向误差模型,从而修正望远镜机械制造安装和光轴变化引起的指向误差[10-11]。常用的望远镜指向误差修正软件有STRAC 和TPOINT 等[12-14],它们基于物理参数及经验修正望远镜指向,但仅利用指向模型进行大型地基望远镜误差修正具有局限性。云南天文台针对1 m 红外太阳望远镜,提出了检测光电导行系统光轴与主光学系统光轴之间相对变化的方法[15]。
从原理上,指向误差可以通过改变主光学系统光轴来补偿,而主镜相对于跟踪架来说位置是固定的,因此,需要改变次镜相对于主镜的空间位置,那么次镜需要在空间5 个自由度上可调。以4 m 望远镜为例,其次镜调整平台为Hexapod平台,具有刚度大、调整自由度多、位置误差不累计等优点[4-5,7-9]。在实际应用中,采用Hexapod 平台调整次镜来校正主次镜光轴变化通常有两种工作模式:一种是闭环模式,如VST[8],以图像传感器反馈的指向误差作为反馈,实时调整次镜的位置;另一种是开环模式,通过望远镜在不同俯仰角度状态下观测恒星,标定出次镜位置,工作时采用查表方式来实现指向误差补偿。4 m 望远镜的跟踪精度要求是0.1(″)/min。尽管设计考虑到了光轴的变化和主次镜光学系统的机械安装弯沉,但当望远镜投入运行时,捕获跟踪器的光轴和主次镜光学系统光轴的相对位置变化并不可知。本文根据4 m 望远镜的结构,分析了闭环跟踪时主光学系统光轴变化引入的跟踪误差的变化规律,提出了望远镜光轴变化的检测方法,并提出基于次镜支撑结构(Hexapod 平台)及卡式系统零彗差点理论的修正模型,来提高地基大口径望远镜的跟踪性能与指向误差修正能力。
2 望远镜系统结构
4 m 级地基望远镜系统如图1(a)所示,总体高度为12.5 m,宽度为5.8 m,质量接近90 t。望远镜主要包括地平式跟踪架、主镜、次镜、机上标定系统、库德系统、机下自适应成像系统及多个成像终端等,这里为了简化分析流程,仅考虑前六部分。望远镜焦面位于机下库德房平台平面,该平台放置4 m 望远镜的多个终端系统,包括精跟踪系统、波前探测系统及高分辨率成像系统。如图1(b)所示,主镜M1 是抛物面反射镜,次镜M2 为双曲面凸反射镜,M3 是椭球平面反射镜,M4~M6 组成库德系统且均为平面反射镜,F1 是主系统焦点,具体的光学参数如表1所示。
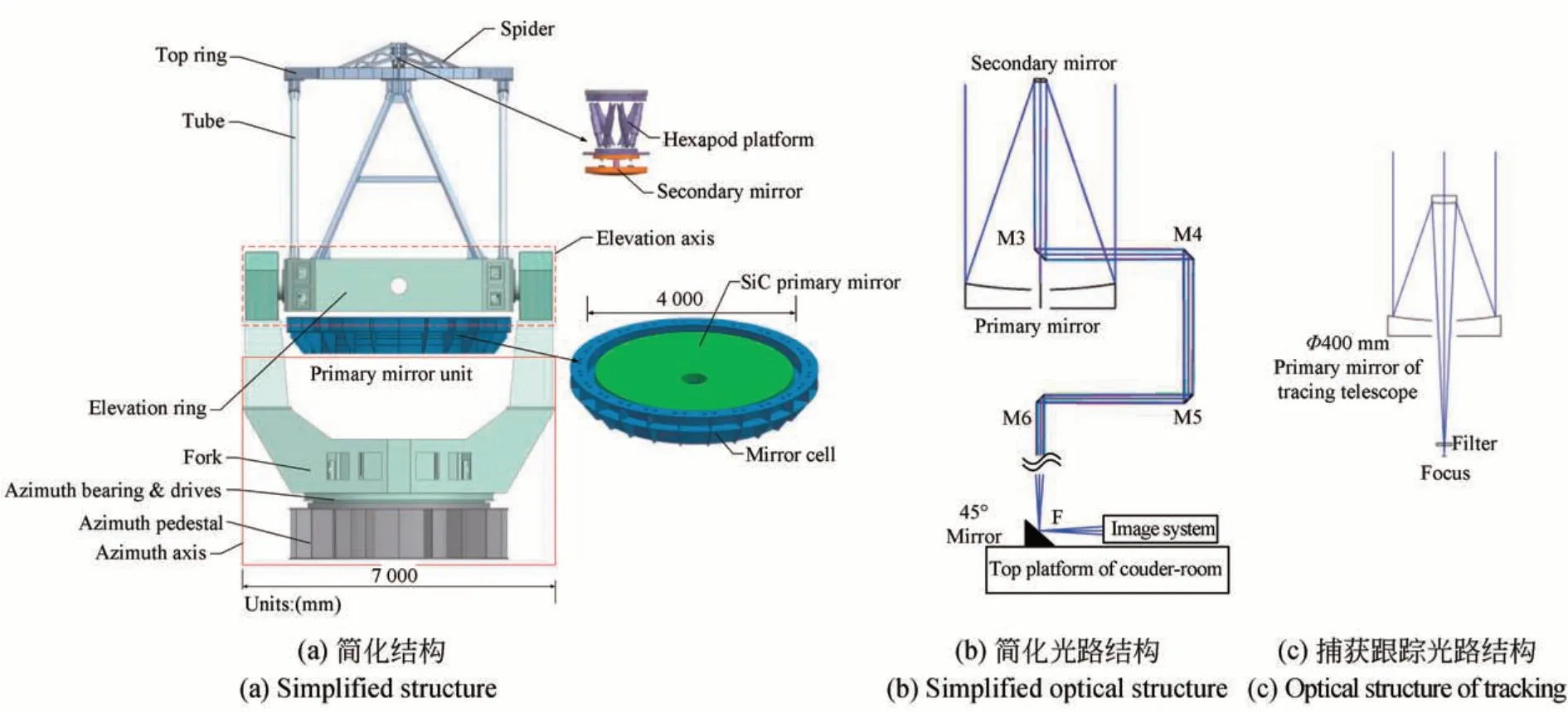
图1 4 米望远镜示意图Fig.1 Schematic diagram of 4 m telescope

表1 4 米望远镜的具体参数Tab.1 Specifications of 4 m telescope
望远镜主镜安装与四通结构内部,四通结构外部装有口径为400 mm 的捕获跟踪器,如图1(c)所示,望远镜系统通过捕捉目标的图像,允许主次镜光学系统在长时间内高精度地追踪区域目标。这种带有独立捕获跟踪系统的闭环追逐模式,需要望远镜主次镜光学系统的光轴和捕捉跟踪器的光轴在整个跟踪过程中应在同一天区内指向一致,即两个光学系统光轴保持严格平行。望远镜通过地平式跟踪架进行观测,为了消除望远镜的准直误差及零点误差,采用对同一恒星的两种状态进行多次观测,两种状态的方位指向相差180°、俯仰指向相差2 倍天顶距,由此可以消除准直误差及零点误差的影响[16]。
图像在望远镜视场内的旋转是大型水平式地基望远镜在目标跟踪时最重要的特征之一。这种旋转除了受望远镜自身光学系统的影响外,还受地平目标系内目标变化规律的影响。
根据图1(b)和图1(c),4 m 望远镜具有库德折转系统,主光学系统与捕获跟踪系统中的像旋转是完全不同的。为了消除像旋对地基望远镜的影响,在4 m 望远镜的成像终端采用道威棱镜消旋系统,消除目标在地平坐标系及库德光路中的像旋。
3 望远镜光轴变化引入的跟踪误差分析
3.1 引起光轴指向变化的因素分析
造成捕获跟踪器与主次镜光学系统光轴改变的原因有许多。首先,支撑主、次镜的桁架结构系统受重力变形引起主镜及次镜之间相对位置变化,从而导致光轴改变[17-19],4 m 望远镜主镜采用主动光学技术实现位置闭环,次镜支撑结构及桁架质量达到2 t,重力引起的形变量是引起光轴变化的主要原因。然后,捕获跟踪器成像终端探测器支撑结构在不同俯仰角条件下受重力影响也会导致光轴变化,4 m 望远镜主系统的成像探测器位于机下平台内,不受重力场变化的影响。最后,400 mm 口径捕获跟踪的质量达到500 kg,捕获跟踪器与望远镜四通接口的安装基座在不同俯仰角下受重力的影响会导致光轴变化[20]。因此,望远镜观测时所有影响因素叠加造成的光轴变化及其规律相当复杂。光轴变化最终会导致捕获跟踪器对目标成像点闭环跟踪后的残余跟踪误差。
现有的光轴变化测量方法有很多[21-24],均是对光学系统特点进行详细分析后得出测量结果。而4 m 望远镜系统的高度达到了12.5 m,采用附加机构对系统光轴变化进行检测是复杂且很难实现的,附加机构不仅存在损坏设备的风险,而且会影响望远镜的正常观测。国外有些学者采用高精度的偏离误差仿真模型来处理大型地基天文望远镜在机械安装与调试过程中引入的跟踪与指向误差,如望远镜主次镜之间的光轴变化引入的相对位置变化偏差。常用的望远镜指向误差修正软件有STARCA 和TPOINT,它们采用的是经验修正及参数修正,精度相对较低。光轴变化引起的误差与望远镜方位轴和俯仰轴不是垂直正交的实际情况有很大关联,并且指向精确度模型只针对望远镜主次镜光学系统的光轴变化进行补偿。4 m 望远镜还要考虑捕获跟踪系统偏差和其他因素导致的光轴变化,即主光学系统的光轴与捕获跟踪器光轴之间的相对变化。
3.2 重力变形引入光轴偏差分析
本文采用有限元法建立望远镜不同俯仰角条件下的结构模型,如图2 所示。该状态下视为准静态模型[25],结构力学方程可以表达为:

图2 望远镜结构的有限元模型Fig. 2 Finite element model of four-meter telescope
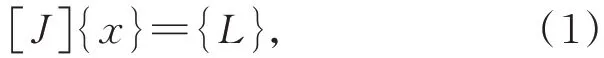
式中:[J]为望远镜刚度矩阵,{x}为位移向量,{L}为载荷向量。
在望远镜观测过程中,引起光轴变化的主要原因是主次镜相对位置的改变,因此在对望远镜进行结构建模仿真时更关注次镜相对于主镜镜面节点的位置变化。以主镜为基准,次镜相对于主镜选取节点位移可表达为:
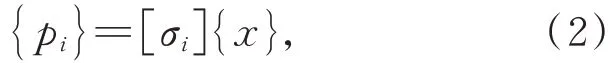
式中:{pi}为次镜镜面节点位移向量,[σi]为次镜相关的旋转矩阵。
由式(1)和式(2)可知,次镜相对于主镜的位置表达为:

式(3)给出了相对于主镜次镜镜面上各个节点的位置信息,根据次镜的二次曲面公式进行最小二乘法拟合可得到次镜相对于主镜的空间位置,得出主次镜在不同俯仰角度情况下的角度偏差仿真结果,如图3 所示,位置偏差仿真结果如图4 所示。

图3 主次镜角度偏差随俯望远镜仰角度的变化Fig.3 Angle deviations between primary and secondary mirror vs. elevation angle of telescope

图4 主次镜位置偏差随望远镜俯仰角度的变化Fig.4 Position deviations between primary and secondary mirror vs. elevation angle of telescope
将仿真分析结果中的位置偏差及角度偏差作为输入,分析望远镜光学模型中主系统的光轴偏差,光轴偏差随俯仰角的变化如图5 所示。

图5 主系统光轴偏差随望远镜俯仰角的变化Fig.5 Optical axis change of primary optical system vs.elevation angle of telescope
3.3 光轴指向变化测量原理
根据上述分析,引起光轴指向变化的主要因素为次镜相对于主镜的倾斜及平移、跟踪探测器与主系统光轴倾斜,如图6 所示。次镜相对于主镜产生的位移为h1,次镜相对于主镜产生的倾斜为θ1,捕获跟踪器相对于主系统光轴倾斜为θ2,它们对目标在成像CCD 上的影响为[25]:

图6 主系统与跟踪器倾斜和平移示意图Fig.6 Relative rotation and displacement between primary optical system and tracking optics
其中:S为次镜到成像CCD 的距离,R为次镜曲率半径,F1为捕获跟踪器的焦距。
为了简化,将捕获跟踪器光轴与主系统光轴倾斜偏差统一考虑为重力场变化带来的指向误差,在观测过程中这部分指向误差可以通过移动次镜来补偿。考虑到4 m 望远镜高度达到12.5 m,在次镜位置放置标定光源是简单且可行的方案。标定光源位于次镜中心位置,在主光学系统装调过程中,通过基准转移的方式使标定光源与主光学系统光轴重合。光源发出的光随着次镜及桁架移动,经过三镜及库德系统将光束折转至机下成像探测器。光轴指向变化测量光路如图7所示。

图7 测定光轴指向变化示意图Fig.7 Schematic diagram of determining telescope optical axis change
模拟光源与目标成像所经过的路径唯一的区别为目标成像经过主次镜进行成像,而模拟光源没有经过主次镜。在模拟光源光轴与主光学系统光轴重合的前提下,标定光源和目标成像的影响基本相同,均可通过标定光源的相对测量进行修正。图像采集步骤为:标定光源随俯仰角变化(间隔5°俯仰角)采集10 幅图像,针对恒星随俯仰角变化(间隔5°俯仰角)采集50 幅图像。在此过程中,望远镜系统状态是固定不变的,俯仰角变化前后采集图像平均坐标值的差值即为望远镜主系统的光轴指向变化。
4 实验与结果
对4 m 望远镜光轴指向变化进行实测与分析,图8 和图9 分别为标定光源与恒星图像脱靶量随望远镜俯仰角的变化值。由图可知,两者基本呈二次曲线变化,与分析结果相符合。在对恒星标校过程中,低于20°俯仰角时4 m 口径望远镜色散现象明显[21],成像系统脱靶量提取精度下降,因此在恒星俯仰角为20~85°时对望远镜进行标定。

图8 标定光源测定光轴指向随望远镜俯仰角的变化Fig.8 Optical axis change of primary optical system by light source vs. angle of telescope elevation

图9 恒星像测定光轴指向随望远镜俯仰角的变化Fig.9 Optical axis change of primary optical system by star vs. elevation angle of telescope
望远镜装配过程中,在俯仰角为45°时对捕获跟踪器与主光学系统进行标校,并以此时的光轴为基准零点。俯仰角较高时望远镜指向变化不明显,而在低仰角工作时望远镜的指向变化幅值较大,这是因为望远镜桁架结构受重力的影响,低仰角时整体力矩变大从而对望远镜指向影响较大。
实验结果表明,望远镜低仰角时,光轴最大相对变化为126″,望远镜桁架结构在重力场的变化是引起俯仰角相关指向变化的主要因素。由于4 m 望远镜整体尺寸较大,光学系统光路总长达到50 m 以上,偏离拟合趋势的采样点对应望远镜主系统及库德光路中大气异常折射及望远镜低频扰动的影响,真实地反映了望远镜光学指向不随俯仰角变化的系统误差。对比标定光源与恒星像取得的数据,在相同俯仰角下恒星像的光轴指向变化比标定光源要小。考虑到采集数据时标定光源安装在次镜桁架结构上,随着望远镜桁架结构在重力作用下运动,因此采样数据存在一定的偏差,在数据处理过程中要以实际测量的恒星像为主。
5 望远镜光轴补偿与分析
5.1 基于卡式系统零彗差点理论的修正模型
卡式结构的望远镜系统在光轴上发生位移,像差体现为离焦和球差,它们可以通过在轴向移动副镜来校正。垂直光轴发生位移和倾斜,像差是视场内的恒定彗差,可以通过在垂直光轴上移动或倾斜副镜来校正。如果不考虑镜面面形的修正,望远镜系统误差为主、次镜的相对位置误差。对于在轴上的视场,如果校正了像差,主、次镜的中心轴相交于零彗星点[22],如图10 所示。

图10 零彗差点示意图Fig.10 Schematic diagram of coma-free point
零彗差点与理想情况下次镜中心顶点距离Zcfp满足:

式中:L为理想情况下次镜中心顶点与焦面中心的距离,m2为次镜放大率,即系统焦距与主镜焦距之比,满足m2=f'/f1',f'为望远镜系统的焦距,f1'为主镜的焦距,bs2为次镜的非球面系数。若绕该点旋转,次镜的平移D和旋转T产生的彗差在轴上视场始终可以相互抵消,但此时次镜相对于主镜的相对位置发生变化,改变了望远镜主光学系统的光轴。因此,在轴上视场得到校正前提下,通过次镜绕零彗差点旋转可以改变主光学系统的指向。以望远镜机下平台成像探测器脱靶量为反馈,作为确定光轴的校正依据,最终实现望远镜指向的修正。
5.2 望远镜光轴补偿结果与讨论
根据次镜当前位置,利用无彗差点理论计算主次镜的无彗差旋转点位置。以无彗差旋转点为基准,以机下成像相机脱靶量为反馈,计算Hexapod 平台各个维度的输入量,对地基大口径望远镜主次镜引起的光轴偏差进行补偿。补偿后,望远镜次镜相对于主镜光轴角度偏差随俯仰角度的变化如图11 所示,位置偏差随俯仰角度变化如图12 所示,望远镜主系统光轴偏差随俯仰角的变化如图13 所示。
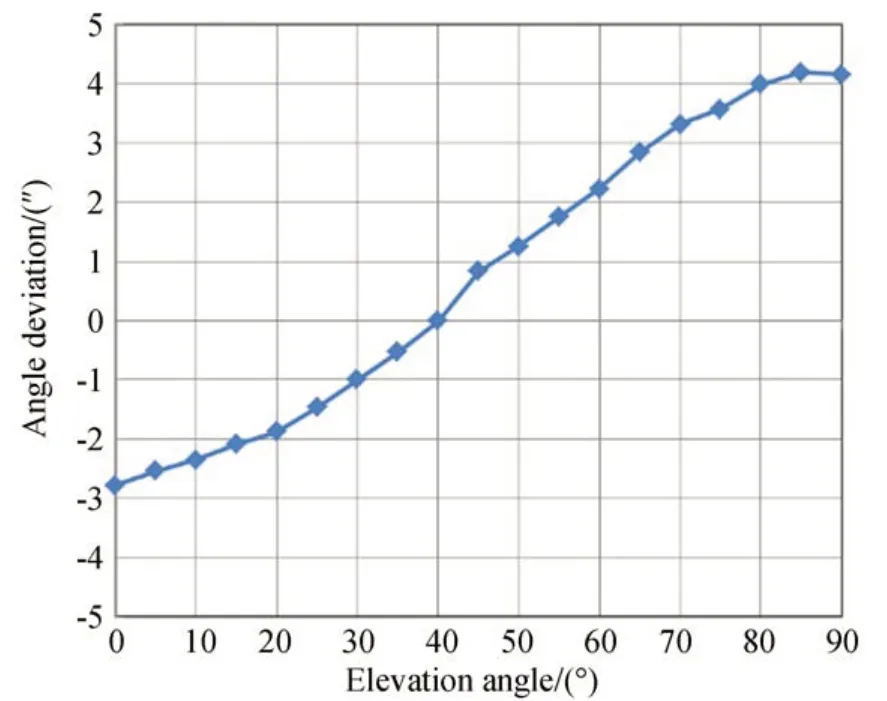
图11 补偿后次镜相对于主镜光轴角度偏差随俯仰角度的变化Fig.11 Angle deviations between primary and secondary mirror after calibration vs. elevation angle of telescope

图12 补偿后次镜相对于主镜位置偏差随俯仰角度的变化Fig.12 Position deviations between primary and secondary mirror after calibration vs. elevation angle of telescope

图13 补偿后主系统光轴偏差随俯仰角的变化Fig. 13 Optical axis change of primary optical system after calibration vs. angle of telescope elevation
补偿前,在光轴水平位置次镜相对于主镜为最大位置偏差和最大角度偏差,最大角度偏差接近39″,最大位置偏差接近0.5 mm;经过Hexapod 平台的补偿,最大角度偏差下降到7.1″,最大位置偏差下降到0.017 5 mm;与角度偏差相比,补偿后位置偏差下降较少,仅由0.5 mm 下降到0.017 5 mm。这是由于在非线性最小二乘拟合过程中忽略次镜二次曲面拟合误差的原因,非线性球面拟合来表达次镜表面节点位置信息,以拟合曲面中心位置与实际次镜表面二次曲面中心节点的几何连线作为光轴,此模拟光轴与实际光轴存在一定的拟合偏差,因此主、次镜的相对位置在初始时便存在一定的偏差。
基于卡式系统主次镜零彗差点理论将次镜绕无彗差点旋转进行光轴补偿,不会改变主系统像质,只改变主系统光轴,其实质为次镜光轴与主镜光轴的对准。补偿前光轴最大偏差为123″,补偿后光轴最大偏差下降至2.8″。
6 结 论
本文针对地基大型光学望远镜中重力变形导致的光轴偏移,研究了捕获跟踪系统与主光学系统光轴偏移的估计、光轴偏差的检测方法及基于次镜支撑结构(Hexapod 平台)调整平台的主动补偿过程。基于有限元方法建立了地基望远镜的结构模型,研究了系统光轴指向变化的产生原因、标定及补偿,提出了基于卡式系统主次镜零彗差点理论将次镜绕无彗差点旋转进行光轴补偿的方法。实验结果表明:重力变形是导致主光学系统光轴偏移的主要原因,光轴偏移量达到了123″,经过次镜位置补偿及无彗差点旋转补偿,光轴偏移问题得到明显改善,光轴偏移量下降至2.8″。本文提出的地基大口径望远镜指向变化检测与修正方法可应用于实际望远镜的标定和装调中。
