基于改进粒子群算法的配电站低压故障实时监测方法

闫振华，罗海荣，何鹏飞，田永兴，张亚杰

（1.国网宁夏电力有限公司电力科学研究院，宁夏 银川 750001；2.国网宁夏电力有限公司，宁夏 银川 750001）

0 引 言

传统的低压绝缘配电站故障监测方法通过安装传感器与低压检测装置，实现对配电站低压故障的监测[1]。随着分布式电源的并网接入，配电站的电网规模不断扩大，电气设备之间的线路连接方式也越来越复杂。传统的配电站低压故障监测方法已经无法满足快速精准的故障监测需求，存在耗时较长、成本较高、监测步骤烦琐、监测周期较长等弊端。同时由于传统的故障监测方法通过设置回路抗阻值来判定是否发生故障，无法保证故障节点的定位精度，不利于配电站电力系统的日常运行与安全维护[2,3]。因此，为满足配电站运行的维护需求，需提高低压故障监测的定位精度，开发出一种快速准确的故障定位方法，实现对配电站的高效监测。粒子群算法由于其强大的捕捉性能，被广泛应用在各种故障定位监测技术中。但是由于粒子群算法在对节点进行捕捉获取的过程中容易出现局部收敛的情况，导致节点定位精度受到影响。因此需要对粒子群算法进行优化，旨在提高节点捕捉精度，并与配电站低压故障监测技术进行结合，减小配电站因低压故障带来的经济损失。

1 配电站低压故障实时监测方法

1.1 配电站数据采集与预处理

为实现对配电站低压故障的实时监测，首先需要对配电站的相关数据进行采集与预处理，为监测提供数据来源[4]。配电站系统中的数据种类繁多，容易产生较多的无效数据。对此需要选择主要特征参数，包括相电压、相电流、三相电压不平衡度、三相电流不平衡度以及开关量状态等。除无效数据外，配电站数据中还会存在由于各种主客观因素导致的意外数据，例如由操作人员失误拉闸导致断电而生成的数据属于意外数据，该部分数据对配电站监测的参考价值较低，应对其进行剔除，从而保证监测的精度与质量。具体处理手段为异常值平滑以及特征归一化，处理步骤如下。

受到配电站较为复杂的配电环境影响，部分数据会出现异常波动导致噪声值偏大，不利于对配电站低压故障情况进行监测[5]。因此，需要对异常数据值进行处理，具体有2种手段。其中1种是直接进行剔除，但是剔除后数据集的连贯性会受到影响。因此利用与异常数据时间相近的正常数据作为权重值，对异常数据进行平滑化处理，具体处理公式为

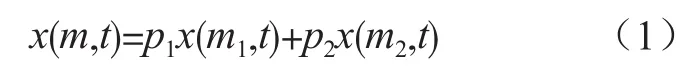
式中：x(m,t)代表第m天t时刻内对应的配电站数据特征指标；p1x(m1,t)与p2x(m2,t)分别代表第m-1天与第m+1天对应的配电站数据特征指标。将异常值前后2天的正常数据作为权重值，可实现对异常值的平滑化处理，得到较为稳定的数据[6]。

由于配电站数据特征参数的取值范围和单位等属性存在一定程度的差异，属性上的差异导致数据覆盖，例如取值范围较小的参数会被范围较大的特征参数覆盖掉，导致最终的监测结果受到影响。因此需要对特征参数进行归一化处理，具体处理公式为

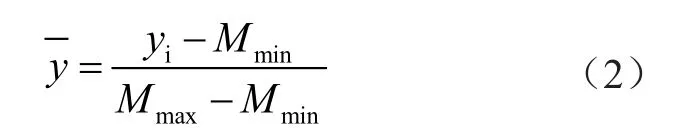
式中：yi代表特征参数M的实际值；Mmin与Mmax分别代表特征参数M的最小值与最大值；代表归一化后的特征参数，其取值范围为∈ [0,1]。

通过上述步骤即可实现对配电站数据的采集与预处理，得到较为稳定可靠的配电站特征参数，为后续的配电站低压故障监测提供数据来源。

1.2 基于改进粒子群算法的配电站低压故障定位

运用粒子群算法实现对配电站低压故障定位原理在于，通过分析求解网络内各节点的运行状态，得到故障区段的节点位置。但是由于粒子群算法在解决该类问题时通常存在局部收敛的弊端，因此需要对其进行改进。通过在算法中加入进化因子，对局部收敛的状态进行判断，可有效规避局部收敛对算法效果的不利影响。对此，定义粒子群算法的进化因子为f，具体表达式为

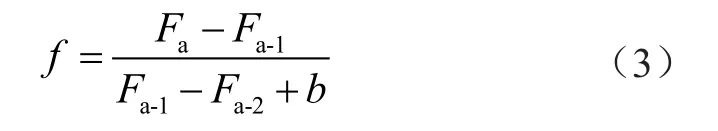
式中：Fa代表粒子群算法在进行第a次运算时的最佳适应度值；b代表平滑系数，取值范围为b∈(0,1)。通过式（3）可以看出，当粒子群算法中进化因子的值为0时，粒子群不再进化；当进化因子的值大于0或1时，粒子群处于正向进化或加速进化状态；当进化因子的值在（0,1]时，粒子群处于正向进化状态，但进化速度逐步递减；当进化因子的值在[0,1]时，粒子群存在局部收敛的情况，此时粒子群需分离出部分粒子进行探索。

通过上述步骤即可实现对粒子群算法的优化，构造出配电站故障定位的评价函数，具体表达式为

式中：CB代表配电站各种设备的开关状态，其值为0或1；Ii代表第i个设备开关处传输的低压故障电流数据；N代表配电站中的馈线区段个数；I*代表配电站设备开关节点对应的期望状态。

假设配电站馈线区段分别为J1、J2、J3，当配电站出现低压故障时，线路上的所有开关均会检测到故障电流。因此，可构建出各个开关对应的期望函数，具体表达式为

式中：I*(CB1)代表开关节点CB1对应的期望函数。

对此可构建出改进粒子群算法对配电站低压故障的定位流程，具体流程如下。首先，对改进后的粒子群算法进行参数设定，假设规模为N，总体运算次数为T，则可根据式（4）和式（5）编写出配电站中各个串联开关的期望函数与评价函数，得出粒子i在捕食状态下的初始极值为qi，对粒子运动速度进行迭代，迭代后的粒子群初始极值设为qd。假设粒子群的初始位置为Xk=(xk1,xk2,…xkd)，比较2个初始极值的大小，若迭代后的极值大于迭代前的极值，则更新粒子群的定位，对应的公式为

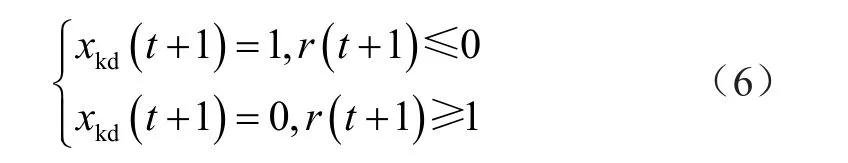
式中：t代表粒子群体的迭代次数；xkd(t+1)代表迭代次数为t+1时的粒子群体运动位置。当t值全部穷尽后，找到的粒子群体的运动位置即为当前低压故障的定位节点。

通过将低压故障定位节点进行实时统计，在检测出故障节点时进行报警，即可实现对配电站低压故障的监测。至此，基于改进粒子群算法的配电站低压故障实时监测方法设计完成。

2 实验环节

为了更好地说明提出的基于改进粒子群算法的配电站低压故障实时监测方法在监测精度上优于传统的低压绝缘监测方法，在理论方面设计完成后，构建实验环节，对该监测方法的实际监测效果进行分析。

2.1 实验环境

本次实验选取的对比对象为基于移动页面加速（Accelerated Mobile Pages，AMP）测量法的低压绝缘故障监测方法，通过对比故障定位精度上的差异，比较2种监测方法的实际监测效果。对此，选取了4种不同的低压故障，分别为单相接地低压故障、两相接地低压故障、两相短路低压故障以及三相短路低压故障。选取配电站的某条线路L，对该线路进行故障布置，线路L的具体负荷曲线如图1所示。

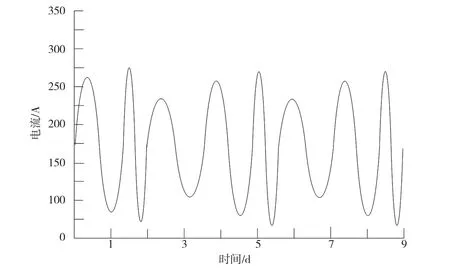
图1 线路L负荷曲线

根据上述提出的方法对配电站的数据进行采集与预处理，针对故障线路L进行模拟检测，比较2种监测方法得到的故障点定位值与实测值之间的误差。

2.2 实验结果

使用2种故障监测方法对线路L进行监测，得到故障节点具体位置，将节点具体位置与实测位置进行对比，得出故障定位误差值，具体对比结果如表1所示。

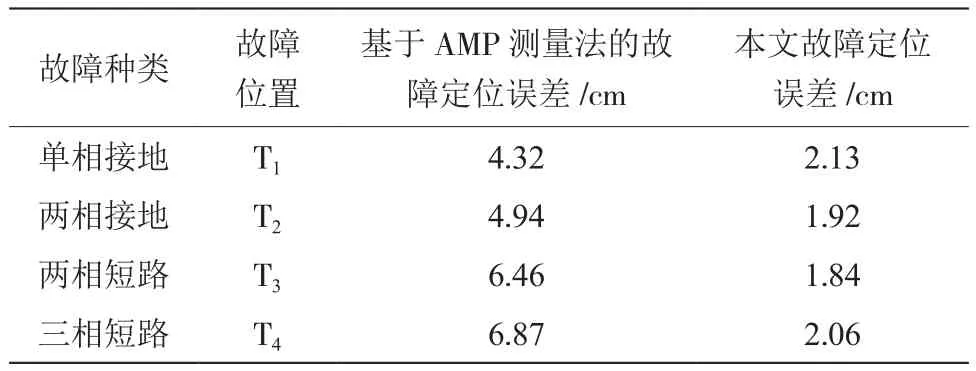
表1 故障定位误差对比

通过上述实验结果可以看出，配电站低压故障监测方法在针对不同的故障类型进行监测定位时，其定位精度也会有所不同。基于AMP测量法的低压绝缘故障监测方法的定位误差均值在5 cm左右，且随着故障种类的不同，故障定位误差波动较大。说明基于AMP测量法的低压绝缘故障监测方法的故障定位稳定性较差，无法实现对多种低压故障监测的精准定位，不利于配电站电力系统运行的维护工作。而本文提出的基于改进粒子群算法的配电站低压故障监测方法在对模拟故障类型进行定位时，定位误差保持在2 cm左右，定位精度明显高于基于AMP测量法的故障监测方法。该故障定位误差不会随着故障类型的改变而出现较大的波动，说明本文提出的低压故障监测方法的稳定性要优于基于AMP测量法的监测方法，在监测精度上更占优势，可为操作人员对低压故障的诊断争取更多时间，对维护配电站正常运行提供技术保障。

3 结 论

本文所提出的配电站低压故障监测方法与粒子群算法进行有效结合。通过对粒子群算法进行优化，规避局部收敛的弊端，减小定位误差，从而实现对故障节点的精确定位，可有效满足配电站低压故障的监测需求。同时该方法在定位速度上也优于基于AMP测量法的监测方法，为配电站的调度提供及时有效的监测定位数据，有利于提高配电站的用电安全。