电子线路中线圈承受瞬态电流的能力分析与研究
2023-01-06黄家毅
黄家毅
(东莞铭普光磁股份有限公司,广东 东莞 523000)
0 引 言
磁性元件作为一种常见的被动元器件,被广泛使用在各种电子电路中。线圈通常指螺旋弹簧状的导线绕组,电子线路中的线圈除了必须满足正常工作的电气特性,还要能够承受“浪涌”或短路工况的瞬态大电流。线圈厂商数据表几乎很少涉及此部分内容。浪涌是因雷击或电源开关通断时,引起的一种尖峰的电流或电压脉冲波。对于电路整机,可以通过电磁兼容浪涌测试来验证其符合性。针对电压浪涌,线圈主要通过材料耐压特性和物理结构就可以初步判定其相应承受能力。但是当电流浪涌出现或短路工况时,线圈将会承受极大电流冲击,这可能将引起绕组温度快速上升并烧毁导线漆膜,导致线圈短路失效。部分文献对变压器的短路电流承受力分析进行报道,并涉及线圈对瞬态大电流(浪涌电流和短路工况)承受力的通用型理论计算和定量分析[1-5]。本文从线圈使用的漆包线承受温度和导体直径参数进行定量分析,给出适用于工程计算的推导过程,并通过热仿真和理论计算值进行对比验证,供线圈开发人员和电路应用人员参考。
1 线圈瞬态电流承受能力分析及计算推导
1.1 瞬态电流波形及绕组温度限值
浪涌作为一种激烈脉冲电压或电流波,分为电压形和电流形2种。汽车EMC测试ISO7637-2适用与12 V和24 V的车辆电气系统和器件抗扰度测试,标准规定了5种测试脉冲,属于中等速度和中等能量的脉冲干扰[6,7]。非汽车类电气系统以及器件则使用《电磁兼容试验和测量技术浪涌(冲击)抗扰度试验》(GB/T 17626.5—2019)标准,其描述的常见波形包括1.2/50μs或10/700μs电压波形和8/20 μs或5/320 μs电流波形。8/20 μs电流波形中,8 μs是上升沿时间,20 μs是半峰值持续时间,详细定义波形如图1短路电流8/20 μs波形曲线所示[8]。8/20 μs是典型雷击穿大地引起的电磁脉冲感应出来过压击穿或烧毁设备时的冲击电流,开关切换或短路电路波形也可使用该波形。因此,线圈承受瞬态电流主要考虑最严格的8/20 μs冲击电流即可。
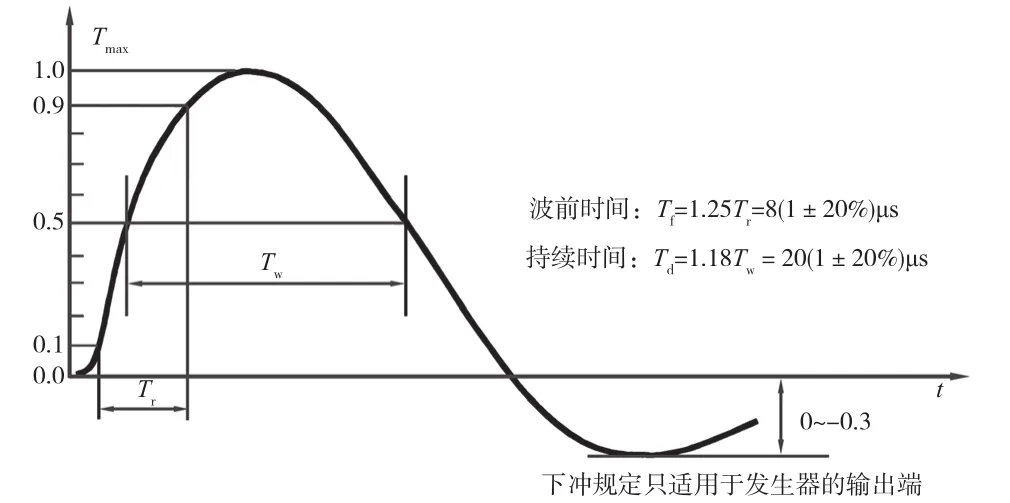
图1 短路电流8/20 μs波形曲线
在瞬态电流冲击下,线圈绕组快速升温,当温度达到一定阀值时,漆膜高分子开始迅速裂解,绝缘能力下降,导致短路。在浪涌(瞬态电流)冲击测试后,其合格判定标准为产品未被损坏,没有安全风险且能自动恢复电气功能并正常工作。现阶段,商用线圈(电感和电子变压器)使用的漆包线都是155 ℃或以上。根据漆包线制造商益利素勒目录中155 ℃(F级) 和180 ℃(H级)等级推荐焊锡温度/时间为2~3/390 ℃,对于0.05 mm G1 P155最低要求为 0.3 s/370 ℃。这里可以理解为完全破坏漆膜需要370 ℃高温持续至少0.2 s。软化击穿温度指的是在一定高温条件下,垂直交叉的2根漆包线,在交点处施加特定的负荷,2 min内不发生击穿绝缘。155 ℃和180 ℃等级软化温度分别为230 ℃和260 ℃,长时间高于其软化温度会损害漆膜绝缘性,长期工程实践表明,在260~350 ℃温度范围内,1~3 s出现3次这样的温升,几乎不会损害其绝缘性。一些文献报道电力变压器短路工况下(短路电流持续时间不超过2 s),130 ℃或以上等级线材绕组温度限值为350 ℃[3,9]。对于F级或以上漆包线绕组其破坏临界点为0.3 s/370 ℃,为了确保其寿命和可靠性,考虑工程余量,F级线圈温度和时间限值为300 ℃,2 s以内,H级则为320 ℃,2 s以内。
1.2 计算推导过程
比热容表示单位质量的某种物质升高(或下降)单位温度时吸收或放出的热量。线圈绕组从常温升高不损伤漆膜承受最高温度所需要热量Q为
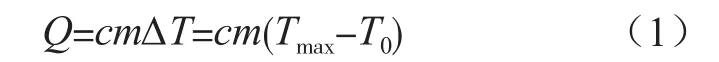
式中:c为铜的比热容,其值为0.39×103J/(kg·℃);m为绕组铜导体的质量,kg;T0为常温20 ℃;Tmax为漆包线在承受最大温度限值,其值为320 ℃。
绕组铜导体的质量m为

式中:ρ为铜的密度;l为绕组铜导体的长度,m;s为铜线导体横截面积,m2。
对于铜导体直径d对应的横截面积s为

当瞬态电流冲击线圈时,忽略交流磁场和邻近效应影响,圈绕组产生热量Qi为

式中:i为瞬态电流,A;RDC为绕组的直流电阻,Ω;时间t为电流持续时间,s。
瞬态电流是一种复杂尖峰电流波形,以GB标准给出8/20 μs数学函数式为例,采用积分方式计算发热量Qi比较复杂和困难,为了简化计算,把瞬态电流等效处理为一种为8/20 μs脉冲宽度的60%且峰值一致的脉冲方波电流I[8]。由式(4)得到等效发热计算式为

而绕组直流电阻RDC为

式中:ρ20为常温20 ℃铜的电阻率,取1.72×10-8Ωm;l为绕组铜导体的长度,m;s为铜线导体横截面积,m2。
若长时间加载电流,在稳态情况,线圈发热和散热同时,其绕组热量Q为
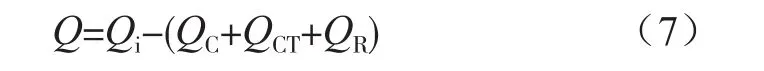
式中:QC为热传导散耗热量;QCT为热对流散耗热量;QR为热辐射散耗热量。
自然对流冷却的对流散热时间一般为4~15 min。瞬态电流时间极短,不可能依靠接触传导将热量传输到其接触材料和环境,传递热量几乎为0。由于绕组表面积较小,铜表面发射率(其值为0.037)很小,在微秒级的时间内,其辐射换热也是极小。因此,在瞬态工况下,QC,QCT,QR都忽略不计,取值均为零,由式(1)、式(2)、式(3)、式(5)、式( 6)、式(7),可得线圈能承受瞬态电流I(ip代表瞬态电流峰值)为
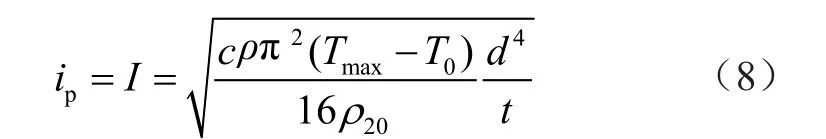
1.3 瞬态电流的计算
根据式(8)可知道线圈承受瞬态电流大小只是跟铜线导体直径d和瞬态电流持续时间t有关。结合上述线圈承受瞬态电流的计算方法,采用等效方波计算,脉冲宽度为12 μs(20 μs×0.6),不同线径(H级)的线圈对于所能承受瞬态电流(8/20 μs及短路工况1 ms电流)的计算值如表1所示。

表1 不同线径线圈承受瞬态电流的计算值
2 计算机瞬态热仿真分析
瞬态工况时间极短,工程上无法通过普通设备实时监控线圈绕组的温度及其变化,为了验证上述理论分析的正确性,目前比较科学的方法是通过计算机进行热仿真分析。
2.1 仿真流程及仿真输入设置
本文中,电磁-热仿真选择多物理场耦合分析平台EMWORKS EMS,整个仿真流程和详细设置过程如下所示[10]。
(1)建立模型:在SOLIDWORKS或 Autodesk Inventor建立1个3D线圈模型(工字形绕线电感),整体尺寸(L×W×H)为6 mm×6 mm×4 mm,绕组模型为环形圆筒,如图2所示。

图2 仿真线圈的模型及剖面
(2)选择分析类型:进入EMS并新建立study,选择分析类型为Transient Magnetic(瞬态磁场) ,并在耦合分析选择Thermal Coupling(热力耦合)分析,整个分析过程持续时间设定为1个周期40μs,步进增量为2μs。
(3)指派材料:磁芯(典型的铁氧体),绕组(铜)。
(4)设置激励:首先电磁输入中设置线圈,绕组类型为Wound coil,线圈驱动类型为电流驱动,绕组线径圈数设定参照表2,瞬态电流采用自定义波形,电流波形如图3所示,波形峰值电流按照表2的值来设定。热输入设置,选择convection(热传导),选中空气域并设置自然散热空气换热系数为10 W/(m2·K),开始温度为 293.15 K(常温20 ℃)。
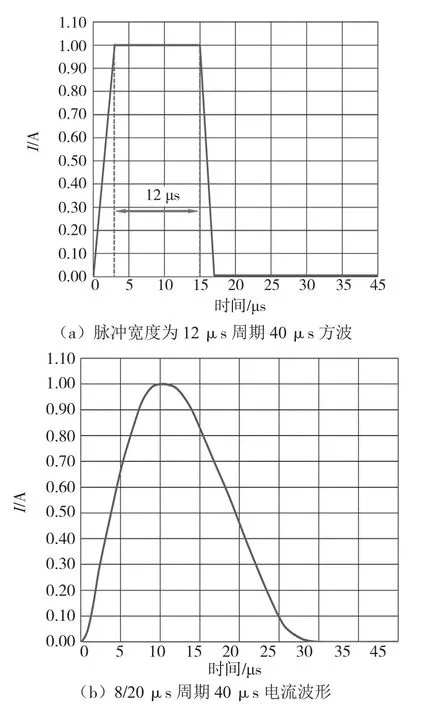
图3 绕组输入瞬态电流波形
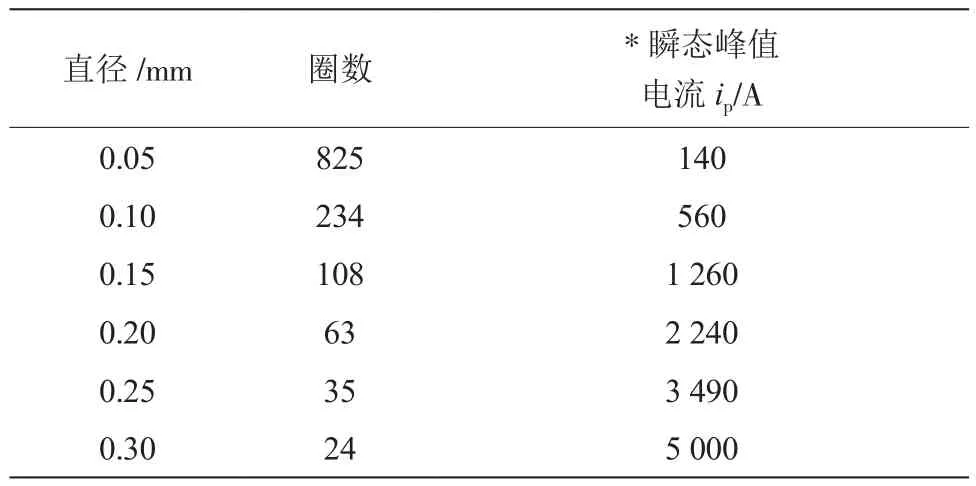
表2 不同线径对应绕组圈数及对应瞬态电流峰值
(5)网格划分:可采用系统自适应网格划分。(6) 检查错误并运行仿真。
2.2 瞬态电流工况热仿真分析
2.2.1 脉冲方波和8/20 μs电流波形(周期均为40 μs)瞬态电流的仿真对比
为了验证12 μs脉冲宽度的方波和8/20 μs电流波形这2种不同波形对相同绕组的温度影响,以绕组0.10 mm×234TS为例,分别施加图4所示的方波和8/20 μs电流波形,分别得到仿真温度分布图,并找出最高温度分布图进行对比。图4(a)中显示方波作用对应的绕组最高温度约为290 ℃,而8/20 μs电流冲击后线圈最高温如图4(b)所示,约为280 ℃,最高温度很接近,这2种的波形热积累效果相当,也证明上文中采用12 μs脉冲宽度40 μs周期波形等效于8/20 μs电流计算方法正确性。
2.2.2 瞬态电流(脉冲方波)的热仿真分析
图5展示了图4(a)瞬态工况下线圈模型在各时间步内整体的温度分布,整1个周期内,磁芯大部分温度仍然维持和环境温度相同,这也说明了瞬态工况,线圈和磁芯接触传导热量极小。对于图4(a)中方波所示16 μs后的电流值为0,发热量则不会再增加,图5(d) 所示20 μs时刻线圈模型最高温约为300 ℃,而图5(e)所示40 μs时刻也约为300 ℃,差别只是绕组中最高温度所在区域面积变小,但前后变化量极小,这也证明微秒级瞬态工况下,在这种尺寸下对流散热和辐射散热数值几乎为0。
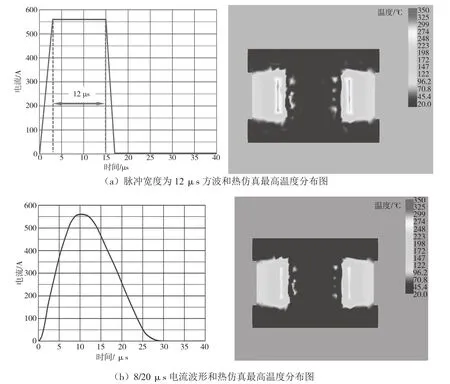
图4 绕组0.10 mm×234 TS的不同输入波形及对应其热仿真最高温度分布图

图5 绕组0.10mm×234 TS瞬态热仿真中各时间温度分布图
2.2.3 不同线径的瞬态电流的热仿真分析
对表2所列的各种不同线径以及在限定320 ℃条件下对应线径计算得到承受瞬态电流最大电流。图6展示了不同线径方波瞬态工况热仿真中最高温度时刻的温度分布图,除了图6(a)和图6(f)展示最小温度约为280 ℃,其余最高温度范围均为290~320 ℃。仿真结果证明了在表1中所列通过式(8)计算瞬态峰值电流的正确性。对于表1中1 ms的瞬态电流,同样方法进行仿真可得对应的线径最高温大约为220~250 ℃,假设320 ℃误差范围为60~100 ℃,主要原因是在相对较长时间维度时,忽略散热影响和非积分求计算发热误差累计造成。因此,瞬态电流持续时间越短,温度或计算电流的误差越小。

图6 不同线径的瞬态热仿真中最高温度时刻的温度分布图
3 结 论
本文对线圈承受瞬态电流能力进行了计算分析,并通过热仿真验证理论计算方法的正确性。虽然本文简易的工程计算和仿真结果存在一定误差(大概7%~18%),但符合工程设计误差要求,瞬态电流周期越短误差越小,且方法简单易用,为相关技术开发和应用人员在工程实践中提供设计参考和帮助。
