基于粒子群算法的城市快速轨道交通线网规划方法
2023-01-06顾小龙
熊 杰,顾小龙
(北京城建设计发展集团股份有限公司深圳分公司,广东 深圳 518049)
0 引 言
城市快速轨道交通相较其他交通方式而言,在解决大中型城市交通压力的问题上具有更加明显的优越性与先进性。现阶段的交通线网规划方法中,存在盲目扩大交通线网服务范围、不考虑客流强度构建高密度的城市快速轨道交通网线的问题,影响轨网运行效率。研究人员分别利用互联网地图数据法、适应性思维法对交通线网进行规划。其中,互联网地图数据法主要是利用可达性评价指标对交通情况进行分析,得出该方法可行的结论[1]。适应性思维法主要是利用适应性理论思维方式,对交通进行整体规划,以此保证规划效果[2]。以上2种方法虽然能够满足人们的出行需求,但是在早晚高峰期间容易受到较大的交通压力影响,增加通行时间[3]。快速轨道交通线网规划过程中,需要根据快速轨道交通特征、交通线网需求等情况,对线网规划方法展开研究。
粒子群算法主要是通过多次迭代,找寻最优解,并通过适应度值来评价最优解的质量[4]。为解决既有城市快速轨道交通线网规划方法中的不足,找到适合城市快速轨道交通规划的方法,本文探索利用粒子群算法,设计城市快速轨道交通线网规划方法。
1 城市快速轨道交通线网规划方法设计
1.1 提取城市快速轨道交通特征
本文主要对影响城市轨道交通线网规划的空间特征进行提取,具体为分析城市交通线网中压力较大的区域后,划分出各个线路的地域范围,将交通系统不断向外延展,在满足城市规划需求的基础上,尽量减少交通压力[5]。本文根据交通出行的地理目标,对线网中各线路进行空间分析,主要的计算公式为

式中:M为交通线路的地理目标;mi为目标线路的位置;xi为目标权重;ni为线路拥堵变化特征分量;N为交通线路的行程距离;yi为交通线路隶属位置向量[6]。根据M与N的值,得出交通线路的空间形态,并划分出不同交通压力的区域。
1.2 预测城市快速轨道交通线网需求
城市交通线网规划过程中主要针对不同区域,如居民楼、商场等人员密集度较高的区域与城郊、偏僻区域等人员密度较低的区域,需要进行差异预测[7]。通过划分出的不同交通压力区域,得出交通扩散通量为
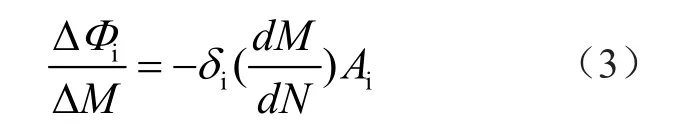
式中:Φi为交通线路通行能力;δi为交通扩散传导系数;Ai为交通线路长度;d为出行距离。结合人员密集区域与人员稀疏区域的交通压力情况,对交通扩散通量进行标定,计算公式为

式中:F为交通量增长标定值;XM为地理目标的线路流动特征;XN为行程距离的条件特征。将ΔF作为基础值,对交通线网需求进行预测,计算公式为

式中:Tij为交通线路中目标线路i到目标线路j的交通分布预测量;s为交通行程约束系数;Gk为目标线路的突发事件总量;rij为目标线路i到目标线路j的交通吸引总量。当Tij值较大时,对其进行分流、截流处理;当Tij值较小时,对其进行引入处理。
1.3 基于粒子群算法构建交通线网规划模型
为了实现城市轨道交通线网高效规划,本文结合交通特征与交通需求预测,利用粒子群算法构建出交通线网规划模型。将交通线网的需求预测数据形成数据集P,将数据集中粒子进行合作与竞争,在n维空间中,粒子i的空间位置设定为Ri,粒子i的速度设定为Vi,则每个粒子的适应度用目标函数来衡量,以此找出最优路径,缩短行程时间[8]。目标函数表达式为
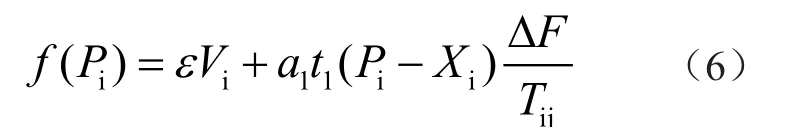
式中:f(Pi)为规划模型的目标函数;ε为惯性因子;a1为加速因子;t1为服从分布的随机变量;Pi为数据集中第i个粒子的历史最佳位置坐标;Xi为粒子i到目前为止出现的最佳坐标位置。规划模型表达式为

式中:Kt为模型约束条件;γmt为模型表达式;εmax为最大惯性因子。在模型中生成粒子轨迹,并将该粒子轨迹中的所有粒子构成粒子群进行迭代,适应度值为0时,迭代完成,此时即为最佳线网最佳规划路径。
2 实 验
为了验证基于粒子群算法的规划方法是否具有实用价值,本文进行了实验,并将实验结果与适应性思维规划方法、互联网地图数据规划方法进行对比。
2.1 实验过程
城市快速轨道交通线网建设主要是为了缓解城市交通压力。在上班、下班通勤期间,城市拥堵现象较为严重,因此较多人选择地铁作为日常的出行方式。
本次实验选择某城市地铁作为测试对象。截取地铁交通线网地图如图1所示,保留原有L1、L2和L3线路,采用本文方法对该轨道交通线网进行规划,得到线路L4,采用适应性思维规划方法规划该轨道交通线网得到线路L5,采用互联网地图数据规划方法规划该轨道交通线网得到线路L6,对其交通特征进行分析。
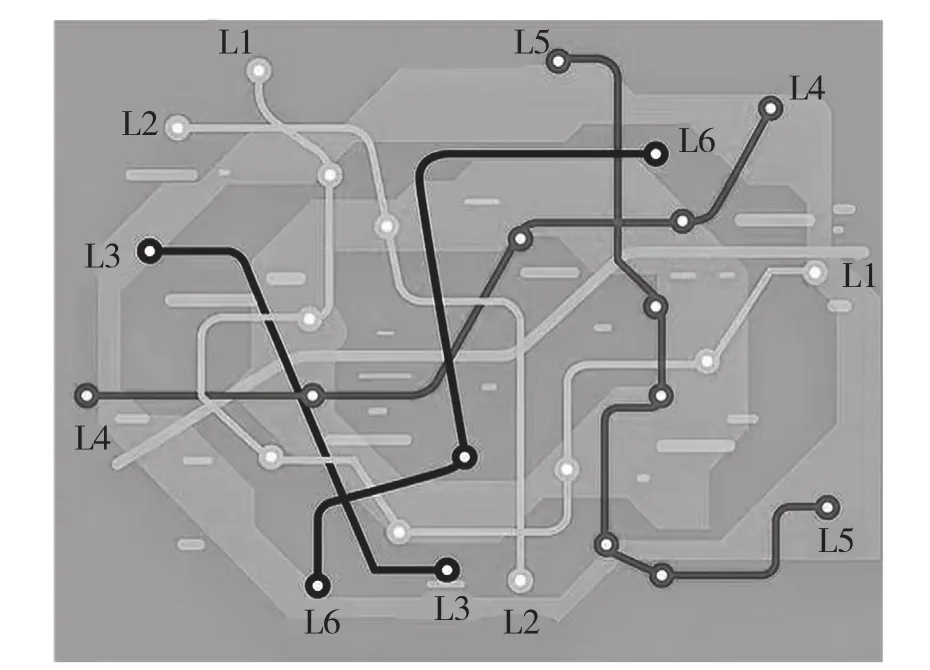
图1 交通线网
本文利用粒子群算法,进行全局最优搜索,得出该规划方法的适应度如图2所示。
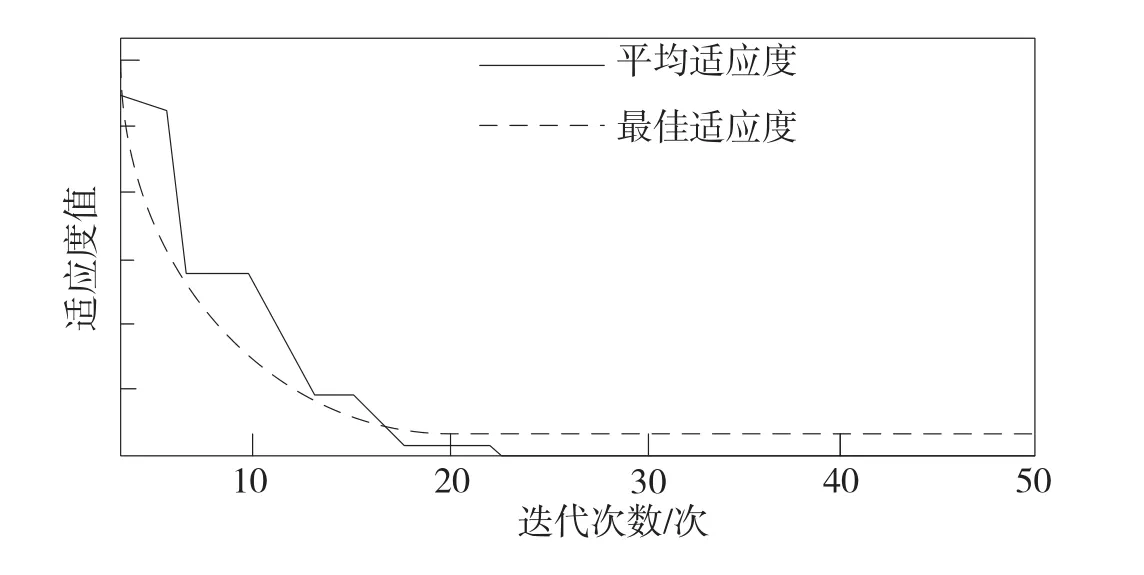
图2 全局最优解
在迭代过程中,适应度值越低,粒子群优化迭代效果越好。本次实验共迭代了50次,平均适应度在迭代第21次之后,适应度值最小,并处于平衡状态,在此处找到了线网规划的最优解;最佳适应度在迭代第19次之后,适应度值最小,并处于平衡状态,在此处找到了线网规划的最优解。结合平均适应度与最佳适应度,本文将迭代次数设定为22次,在此迭代环境下,选取出5~30 km等出行距离,对其通行时间进行分析。
2.2 实验结果
在上述实验条件下,将出行距离划分为7个距离段,在城市快速轨道交通正常通行的前提下,将适应性思维规划方法、互联网地图数据规划方法与本文设计的基于粒子群算法规划方法的城市快速轨道交通行程时间进行对比。行程时间越短,对交通造成的压力越小;行程时间越长,对交通造成的压力越大。一般情况下,在城市快速轨道10 km左右的交通行程中,行程时间在20 min以内为最佳,对交通的压力较小。实验对比结果如表1所示。
如表1所示,完成30 km的行程时间,适应性思维规划方法需要69.52 min,互联网地图数据规划方法需要68.45 min,而基于粒子群算法规划方法需要60.12 min,基于粒子群算法规划方法出行时间最短。从城市快速轨道10 km距离的行程时间来对比,适应性思维规划方法和互联网地图数据规划方法完成行程的时间分别为23.01 min和22.54 min,不满足最佳通行时间20 min内的标准,而基于粒子群算法规划方法为19.23 min,可以满足最佳的通行时间标准。基于粒子群算法规划方法规划的线网交通压力小,线网规划效果较好。
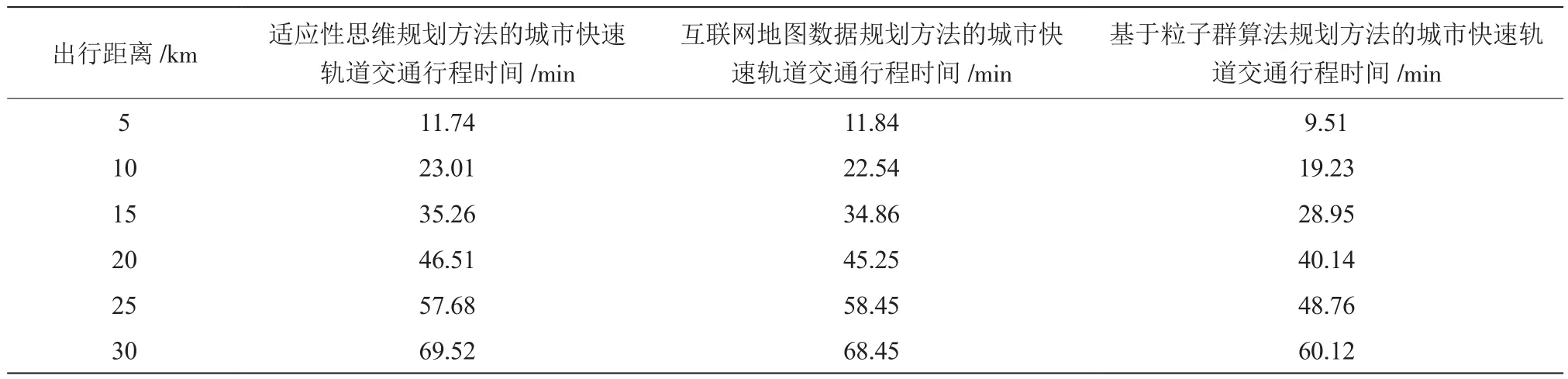
表1 实验结果
3 结 论
现阶段国内轨道交通处于快速发展阶段,早晚高峰交通压力为人们出行带来了极大的不便,本文利用粒子群算法设计了城市快速轨道交通线网规划方法。通过构建交通特征提取模型、需求预测模型、基于粒子群算法的线网规划模型等,建立城市快速轨道交通线网规划方法体系。实验显示,基于粒子群算法的城市快速轨道交通线网规划方法构建的线网有效地缓解了交通压力,缩短居民通行时间,提升轨网运行效率,推动城市快速轨道交通线网规划的发展。
