市场模式下光伏产消者的策略优化
2023-01-06裴柯雯陈盛华
裴柯雯,陈盛华
(河北工业大学 电气工程学院,天津 300401)
0 引 言
目前,能源结构与电力系统运行方式发生了巨大的变化,分布式资源在电网的渗透率不断提高,光伏产消者正在成为分布式光伏与市场经济文献中的研究热点。光伏产消者的新型配电方式为能源管理带来灵活性,有利于改变电能的分布特性,提高电网的供电可靠性。中国目前还处于电力市场建设初级阶段,市场的运营模式、交易机制和实施方法尚不明确。中国电力市场交易规模不断扩大,可支持用户之间的直接交易,多元化市场主体,保证发电侧和售电侧竞争活动有序进行[1]。
产消者在电力系统中发挥着越来越重要的作用,国内外对产消者激励方式、管理框架、交易价格等研究已有一些成果。文献[1]提出的自治消费者社区给予消费者不同平衡溢价的鼓励,以平衡社区电力。文献[2]基于主从博弈理论提出了社区运营商与产消者群组成的社区内能源互联网分布式的能量管理。文献[3]提出了以中国给予光伏电能供需比的内部价格模型。文献[4]提出了一种兼具市场特性和控制功能的机制,即交互能源。这些研究可以优化分布式能源就地利用率,保证电网安全运行,也可以将其结合以保证社会整体效益,但是大多研究较为复杂,在基层社区适用性较低。
本文提出一种基于实时电价的产消者策略优化模型,与上述文献中针对产消者和社区运营商之间交易不同的是,该模型只研究产消者之间的策略问题,更加贴近基层社区情况。该模型有利于调整用户用电策略,实现净负荷的削峰填谷,优化电力结构,减轻电网负担,提高用电安全性,有利于经济运行。同时,光伏一类清洁能源的广泛使用对减轻环境压力,为早日达到“碳达峰”与“碳中和”具有重要的作用。
1 市场模式下产消者交易框架
“产消者”既是消费者又是生产者,他们通过电能与市场调度者产生联系,可以将过量的光伏电能上传到市场,大大提高电能的利用率。本文研究主要针对1个具有提供产消者交易平台的社区,包括拥有电能的市场调度者和几个光伏产消者,具体交易框架如图1所示。

图1 产消者交易示意
市场调度者是产消者交易的运营者,与社区内产消者和电网之间进行电能交易,购买产消者(也可称为“用户”)光伏过量发电的电能,在用户光伏不足时提供电能,储存电能不足可从电网购电来进行供应。市场调度者在管理电能交易这个过程中不消耗电能,通过管理与用户之间交易的电价来赚取差价。
每个用户都有一定的可平移负荷,通过调节每一时刻的可平移负荷量来向市场调度者出售过量的光伏电能,在合理分配电能的过程中获取利益。
2 市场调度者的定价模型
在成熟的电力市场中,电价受需求、供应等形态影响,是一个动态调整过程。本文中,用户通过调整可平移负荷来调整向市场调度者提供的电量,从而改变交易电价。电价是收益的关键因素,相比于尖峰电价,分时电价机制更能反映系统动态供需关系,能够刺激和鼓励用户优化用电方式。因此需要市场调度者制定合适的电价模型来达到与产消者的共赢。
为保证系统优化运行,提高负荷率,应尽量减小系统净负荷波动和峰谷差,即削峰填谷,本文根据净负荷量来制定电价模型。
将1天分为24个时段,1 h为1时段,各时段按照系统运行的平均边际成本来收取电费,电价模型为
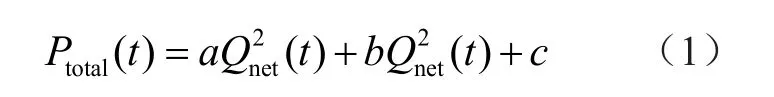
式中:a,b,c为内部交易电价系数;Ptotal(t)为t时段收取的电费总量,Qnet(t)为t时段的净负荷总量为
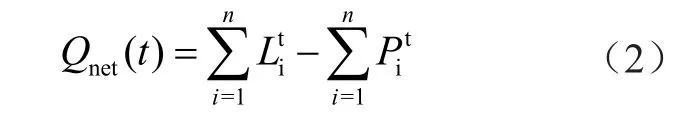
由式(1)可以得到单位电量的电价,由于售电价pcs和购电价pcb的标准不同,因此参数不同,分别可表示为
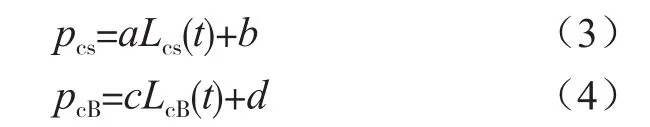
式中:Lcs(t)、LcB(t)分别为t时刻用户售电总量和购电总量;a为负数;c为正数。
3 光伏产消者模型
3.1 负荷模型
本文中的负荷由固定负荷Lf和可平移负荷La这2部分构成,即

固定负荷对可靠性要求较高,且用户用电时间不可改变,不参与需求侧调整。一时间段内,第i个用户的固定负荷数列为
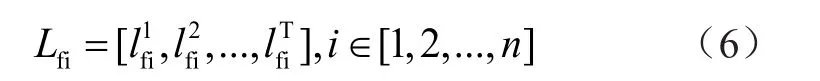
式中:n为用户数量。
可平移负荷为用户可根据电价信息与负荷需求来调整电量和用电时间的部分,满足一定时间内对所需负荷的供应即可。第i 个用户的可平移负荷为
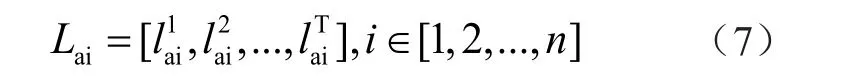
每个时刻的可平移负荷应满足约束条件为

3.2 光伏出力模型
利用改进贝叶斯神经网络的光伏出力概率预测方法可以得到每一时刻的光伏电源有功出力值[5]。第i个用户的光伏出力模型为
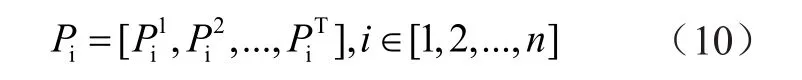
3.3 收益函数模型
该模型主要考虑产消者与市场调度者之间的交易,不考虑产消者直接从电网购电。产消者的收益由政府对新能源发电的补贴、能源消费所带来的用电效益和售、购电费用构成,第i个用户在第t时刻的收益为
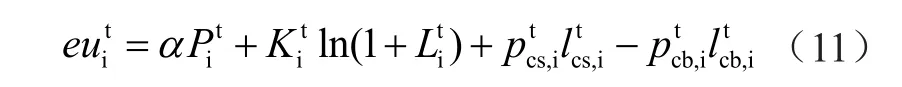
第i个用户的收益为

4 光伏产消者的非合作博弈模型及求解流程
4.1 光伏产消者的非合作博弈模型
在产消者模型中,每个产消者都是独立的利益个体,他们基于实时电价来不断调整不同时刻的可平移负荷,从而达到自身利益最大化。每个产消者的可平移负荷调整都会造成电价的改变,为了最大化所有产消者的利益,本文建立了产消者的非合作博弈模型,从而获得最优策略。
博弈通常包括博弈参与者、行为集合、收益和均衡4个要素,在本模型中4要素具体可表示为:
(1)博弈参与者为n个产消者;
(2)行为集合La1,La2,…,Lan为每个产消者对自身可平移负荷的取值调整策略集合
(3)产消者的收益为{Eu1,Eu2,…,Eun};
(4)博弈的最终解达到纳什均衡。
产消者通过改变自身用电行为,实现非合作博弈的目标函数(即式(11))值最大。
博弈最终求得纳什均衡解,即1个产消者单方面调整自己的行为都不会使自己的收益增加[6]。数学表示为
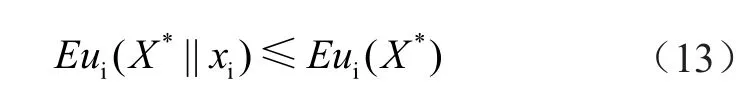
式中:(X*||xi)表示在其他参与者行为不变的情况下改变用户i的行为。
4.2 纳什均衡的存在性证明
设Ei为博弈参与者可出售电量的区间,为凸的有界闭集,当参与者与电能交易时必然存在自身对应的行为集合。
由布劳威尔的不动点定理,Eu为有界闭集之间的连续映射,那么一定存在一个解,使得Eu(x)=x。
该模型中的产消者要面对其他产消者选择的不确定性理性对策,属于混合策略,而在混合策略条件下,纳什均衡一定存在。
由以上2种判断方法,可知该模型的纳什均衡解存在。
4.3 博弈模型求解流程
该模型中需要产消者共同调整实现纳什均衡解的计算,可以将求解用以下数学式表示,即
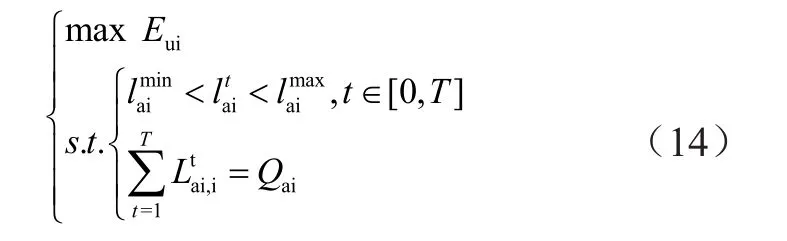
由于将问题进行了只保留电能交易、忽略与电网交易等简化之后求解并不复杂,可以用fmincon函数进行求解,但是迭代次数较多。研究的i个用户依次调整自身可平移负荷,调整过程中电价、收益和负荷在不断更新,在更新后数据的基础上重复上述过程直至达到均衡解。产消者的非合作博弈求解流程如图2所示。
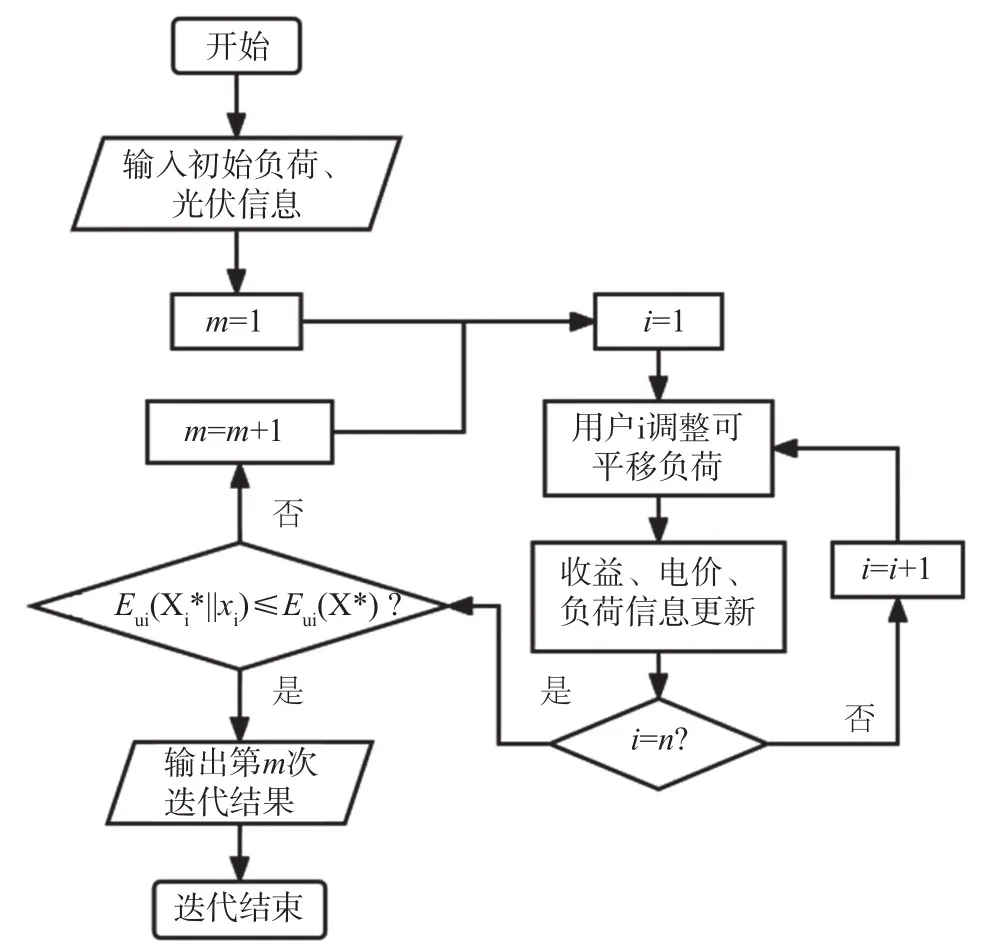
图2 博弈模型求解流程
5 算例分析
5.1 基础数据
本文选取某城市夏季一典型日的负荷和光伏数据进行分析。该社区包含5个光伏产消者,在光伏高峰期均在满足自己需要的基础上有多余光伏电量可出售。各产消者净负荷曲线如图3所示。
由图3可知,各产消者净负荷曲线大体趋势相同,均在10:00-15:00时达到最低,即售电最多。通过模型迭代调整可平移负荷来改变净负荷值,从而达到收益最大化。
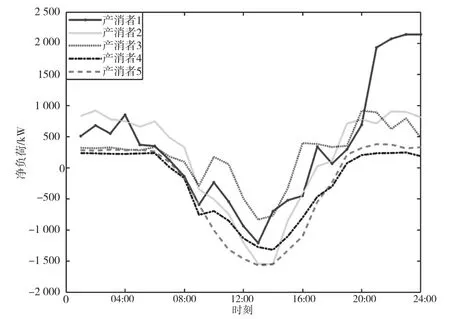
图3 各产消者净负荷曲线
5.2 光伏产消者的最优负荷策略
经过4次迭代后各项数据达到稳定。优化后与初始情况的产消者净负荷对比曲线如图4所示。
由图4可知,经过本文模型的优化,在晚间(20:00-24:00)的负荷峰值有所削减,午时(10:00-15:00时)的负荷谷值有所提升,起到了削峰填谷的作用。
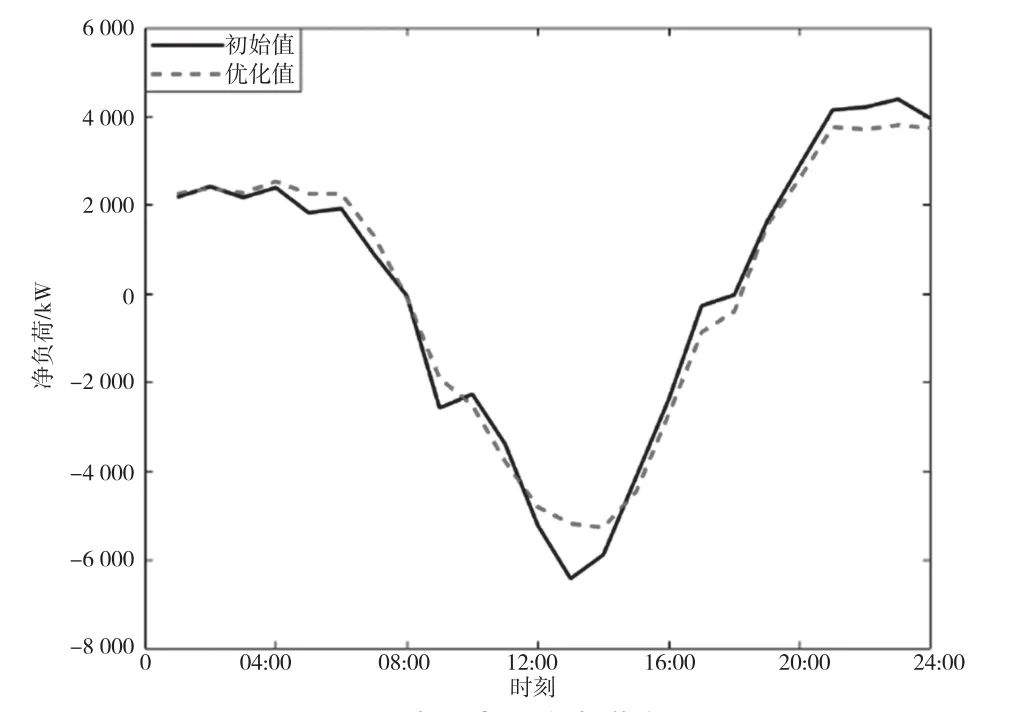
图4 产消者总净负荷曲线
由公式(3)和式(4)可知,电价与用户净负荷紧密联系,晚间购电价较高,所以用户在午时购电,减少晚间用电;午时售电价较低,因此用户增加午时用电,减少售电。这2种情况都会导致午时总净负荷(售电量)减少,晚间总净负荷(购电量)减少,即达到削峰填谷的效果。
5.3 电 价
使用模型前后的售电价与购电价分别如图5、图6所示。
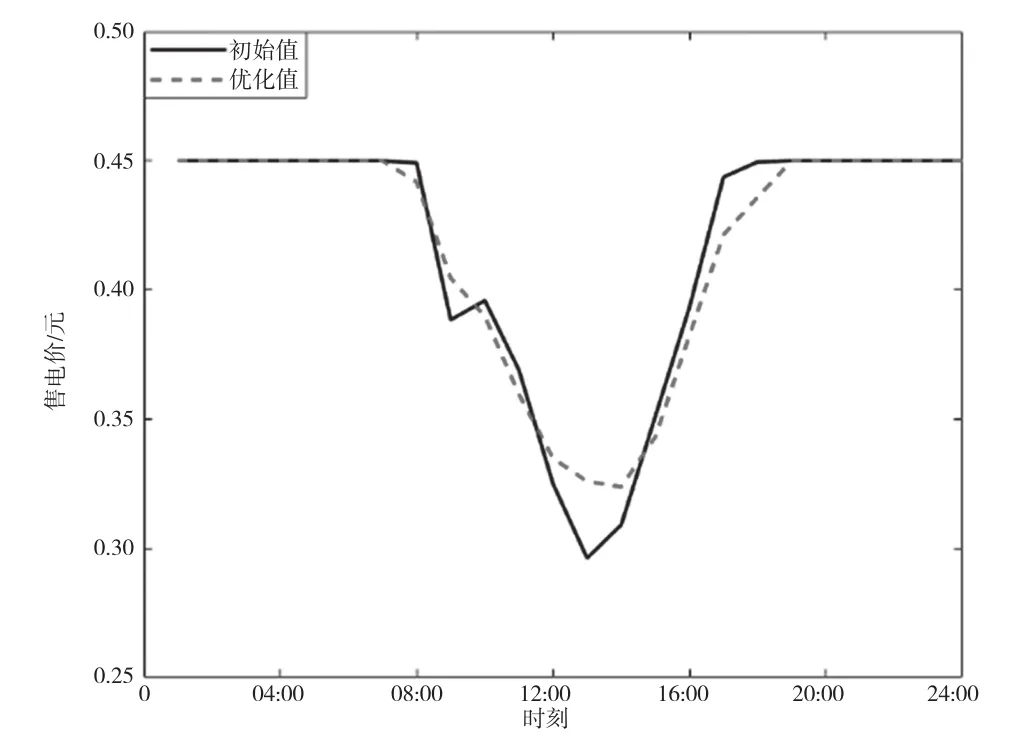
图5 售电价曲线

图6 购电价曲线
将图5与图4进行对比,可以发现在图4净负荷为负时,即开始进行售电时,2个曲线的变化趋势相同;净负荷为正,即进行购电时,图6与图4曲线变化趋势相同。购电量较低时,购电价同样较低,刺激用户消费,购电量高时,购电价变高,降低用户用电消费积极性;同样,售电量较低时,售电价较高,鼓励用户进行电量销售,售电量较高时,售电价变低,限制用户售电。
5.4 光伏产消者的收益
经过优化,各产消者的收益均有不同程度的增长,总收益由初始的102 347.2元增长为优化后的103 183.9元,具体对比如图7和表1所示。
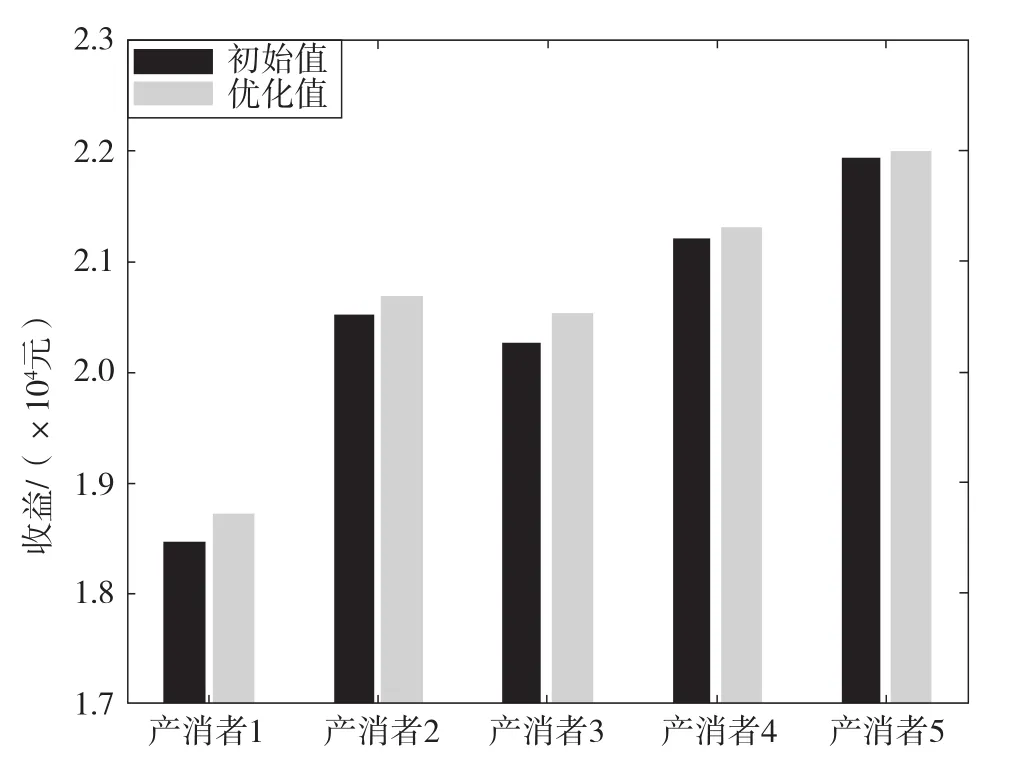
图7 各产消者收益对比柱状图
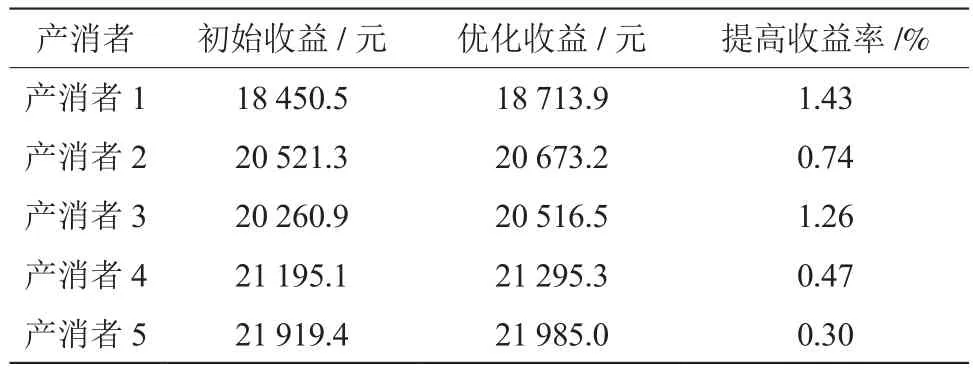
表1 各产消者收益对比
6 结 论
本文以社区产消者为研究对象,提出了基于非合作博弈的电能调整策略优化方法。该模型具有以下优势:(1)只考虑电能传输,符合大部分基层社区的实际情况;(2)在进行模型建立与计算时只涉及用户的净负荷数据,在实际应用时既能保护用户的隐私,又能保证计算的高效便捷。
由算例应用部分可知,本模型对提高产消者收益、优化系统用电负荷均起到了有利作用。
