基于注意力机制优化长短期记忆网络的短期电力负荷预测

王健，易姝慧，刘浩*，王春枝，刘俭，汪根荣

（1中国电力科学研究院有限公司 武汉 430070；2湖北工业大学 计算机学院，武汉 430068）

短期电力负荷预测是电力负荷预测中的不可忽视的一部分，它对不管是过去传统的还是现在智能化的电力系统运行都有举足轻重的作用.在现在开放式的电力市场中，短期负荷预测是保证电力系统经济、安全、稳定运行的有效工具，很多重要的决策都是以短期电力负荷预测结果为基础依据而做出的，比如电力系统的安全性和可靠分析、电力系统的维护保养安排以及发电生产的调度计划等.因此短期电力负荷预测一直是一个值得研究的课题，提高短期电力负荷预测的精确度更成了现代电力行业部门管理和运行的关键.

国外很早就开始了短期电力负荷预测方面的研究，有大量的相关研究文献，文献［1］中ENGLE等人提出了几种回归模型用于预测第二天的负荷数据.文献［2］中RAZAVI和TOLSON等人提出了一种基于神经网络的能源短期负荷预测模型，将历史每小时负荷数据、温度和星期几等作为输入变量，对未来1天到7天的电力负荷分布进行预测.CARPINTEIRO等人［3］提出了一种新的基于层次混合神经网络的电力负荷长期预测模型，它可以应用于需要时间序列分析的领域.文献［4］中提出了相似日的预测方法，该方法基于搜索出近一年、两年或三年内与预测日特征相似的天数的历史数据.文献［5］中时间序列分析方法是电力负荷预测领域的重要手段之一，预测即描述历史数据随时间动态变化的规律，通过建立相关模型来预测未来值.文献［6］中为了提高电力生产效率，研究针对电力负荷预测问题提出了一套综合解决方案，与持久性和搜索算法相结合，建立一个新的集成ultra-short-term电力负荷预测方法基于adaptive-network-based模糊推理系统（简称ANFIS）和反向传播神经网络.

与国外相比，国对电力负荷预测方面的研究起步较晚，但随着经济的发展、科学技术的进步及电力行业一些专家学者不断地研究钻研，电力行业也在快速的发展，电力负荷预测变得更加的精准、智能、精细.文献［7］中先研究了改进的深度信念网络在时间序列数据集的模型，并将改进的模型用于短期电力负荷预测.文献［8］中主要针对短期电力负荷数据非线性部分预测精度低问题提出了基于改进的粒子群算法和深度递归神经网络的短期电力负荷预测模型.文献［9］主要研究的基于神经网络的组合预测模型及其在短期负荷预测方面的应用.文献［10］中提出了一种随机森林与模糊聚类相结合的负荷预测方法，相比于传统的支持向量机和BP神经网络方法，验证了该方法的有效性.文献［11］中提出了支持向量机预测模型、长短期记忆网络预测模型并将二者进行组合的组合预测模型，将模型结合短期电力负荷数据进行验证，实验结果表明二者的组合模型预测结果误差低于2%.

由于短期电力负荷数据属于时间序列数据，故可采取对时间敏感有记忆功能的算法进行预测.但传统的神经网络对于周期较长的时间序列数据容易出现梯度消失或梯度爆炸的问题，故本次对短期负荷预测的研究是基于长短期记忆的神经网络（Long Short Term Memory network，LSTM）进行的.本文的工作内容包括：首先将LSTM结构单元中的隐含层由单一Tanh激活函数改为采用了一种基于权重的混合激活函数组（Tanh函数、Sigmod函数、Relu函数组合），然后采用注意力机制改进LSTM模型用于短期电力负荷预测，能有效挖掘电力负荷数据中的时序信息和变化规律.实验结果显示，改进后的模型预测准确度更高.

1 电力负荷数据及预处理

本次实验的电力负荷数据取自某地的电力负荷集，数据集包含了地区1和地区2从2009年1月1日至2015年1月10日的电力负荷数据以及2012年1月1日至2015年1月17日的天气因素数据.电力负荷数据是每15分钟进行一次采样，每日96次采样，电力负荷单位为MW.天气因素主要包括：日最高温度、日最低温度、日平均温度、日相对湿度以及日降雨量.本次实验选取了某地区1的数据，电力负荷数据有2208行97列，气象数据有1113行6列.

1.1 电力负荷特点

由于2015年的日负荷数据只有1个月的，所以只选取了2009年至2014年以天为单位的日电力负荷数据来观察每年的电力负荷变化，如图1所示.

从图1可以看出，2009年至2014年，每年的电力负荷数据呈现的波形都类似，在每年的1月份到3月份中间都会出现一次波谷，最大负荷的峰值出现在5月份到10月份之间，负荷的变化规律成锯齿状，波形呈现出周期性.

另外从图1还可以看出电力负荷数据具有一定的连续性，没有看到阶跃或离散的数据现象，这是由电网系统对发电、输送电及用电过程的稳定性要求所决定的.电力负荷数据的连续性、周期性的特点，是电力负荷能够被预测的前提和基础，其特点也是电力数据本身固有自带的特性.

1.2 电力负荷影响因素相关性分析

负荷预测的基本原则是确保负荷预测技术的科学性的先决条件，是预测方案产生的基础［12］.本次实验中的电力负荷数据从图1可以看出：有明显的周期规律但也有明显的波动，影响电力数据波动的原因就是外界因素的影响，如本次数据中所体现的外在因素主要是天气因素如日最高温度、日最低温度、日平均温度、日降雨量、日相对湿度等.要想提高短期负荷预测的精度，就要研究这些外在因素与负荷数据之间相关性的大小，找出相关性大的影响因素，将其作为特征作为输入，以提高负荷预测模型的精度.

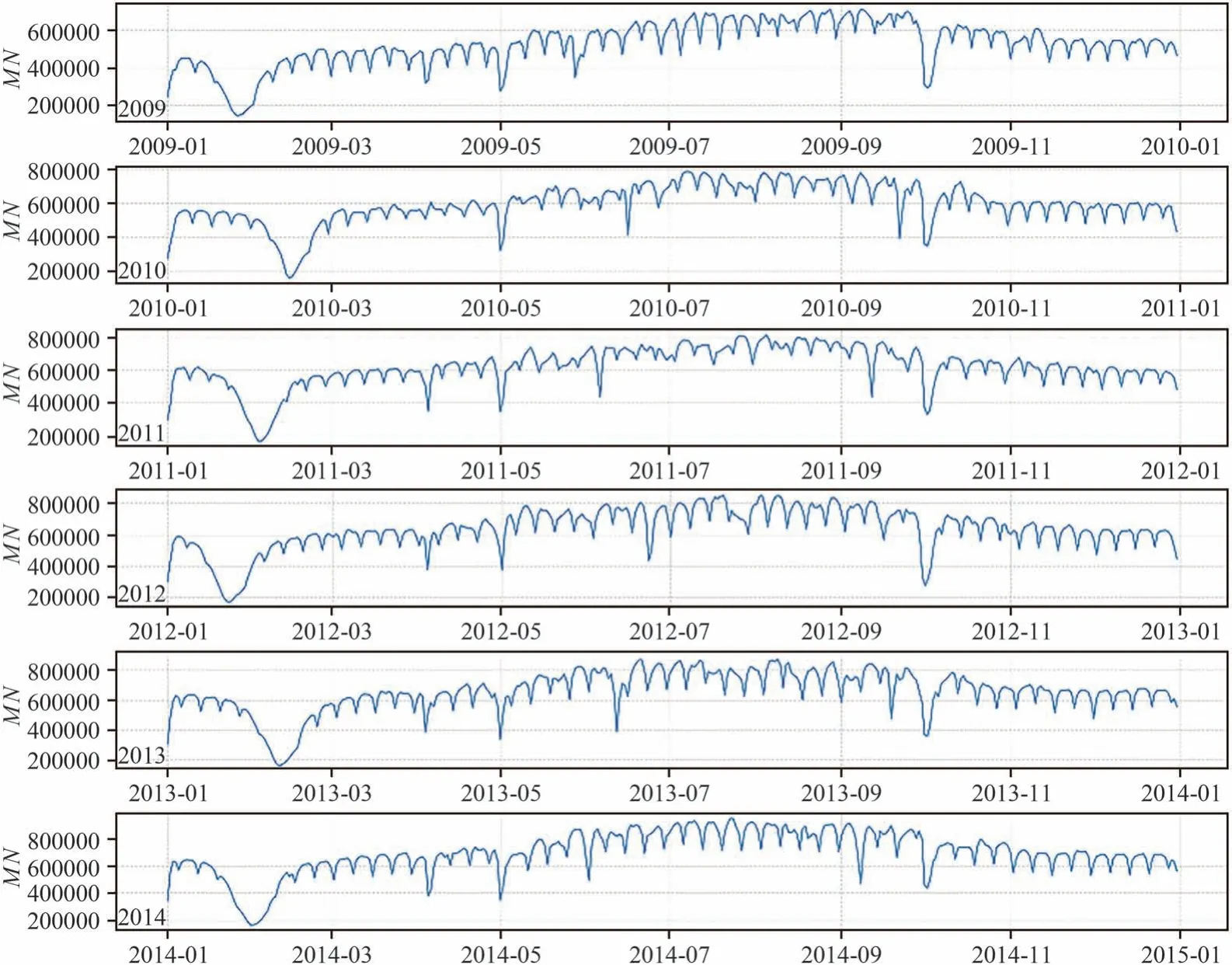
图1 2009年至2014年负荷数据Fig.1 Load datafrom 2009 to2014

为了观察天气因素中的日最高温度、日最低温度、日平均温度、日降雨量及日相对湿度与电力负荷数据之间的相关度，将天气因素数据［13-14］与电力负荷数据合并到一张表格中并将日最高温度、日最低温度、日平均温度、日降雨量及日相对湿度与日最高负荷、最低负荷、平均负荷、日负荷9个特征绘制了2012年至2014年共1096天的9个特征子图，如图2所示.

通过观察图2可以看出，日最大温度、日平均温度、日最低温度的波动曲线比较类似，且日平均温度、日最高温度、日最低温度的波动曲线与日最高负荷、日最低负荷、日平均负荷、日总负荷的变化曲线的变化趋势比较同步，随着日平均温度、日最高温度、日最低温度的上升，负荷值也跟着上升；随着日平均温度、日最高温度、日最低温度的下降负荷值也跟着下降，这说明日平均温度、日最高温度、日最低温度与电力负荷量存在着很强的相关性.经观察相对湿度与电力负荷也存在着一定的相关性，但较弱，降雨量与电力负荷的相关度更弱.为了进一步说明特征之间具体的相关性，下面将对相关性的系数进行计算.

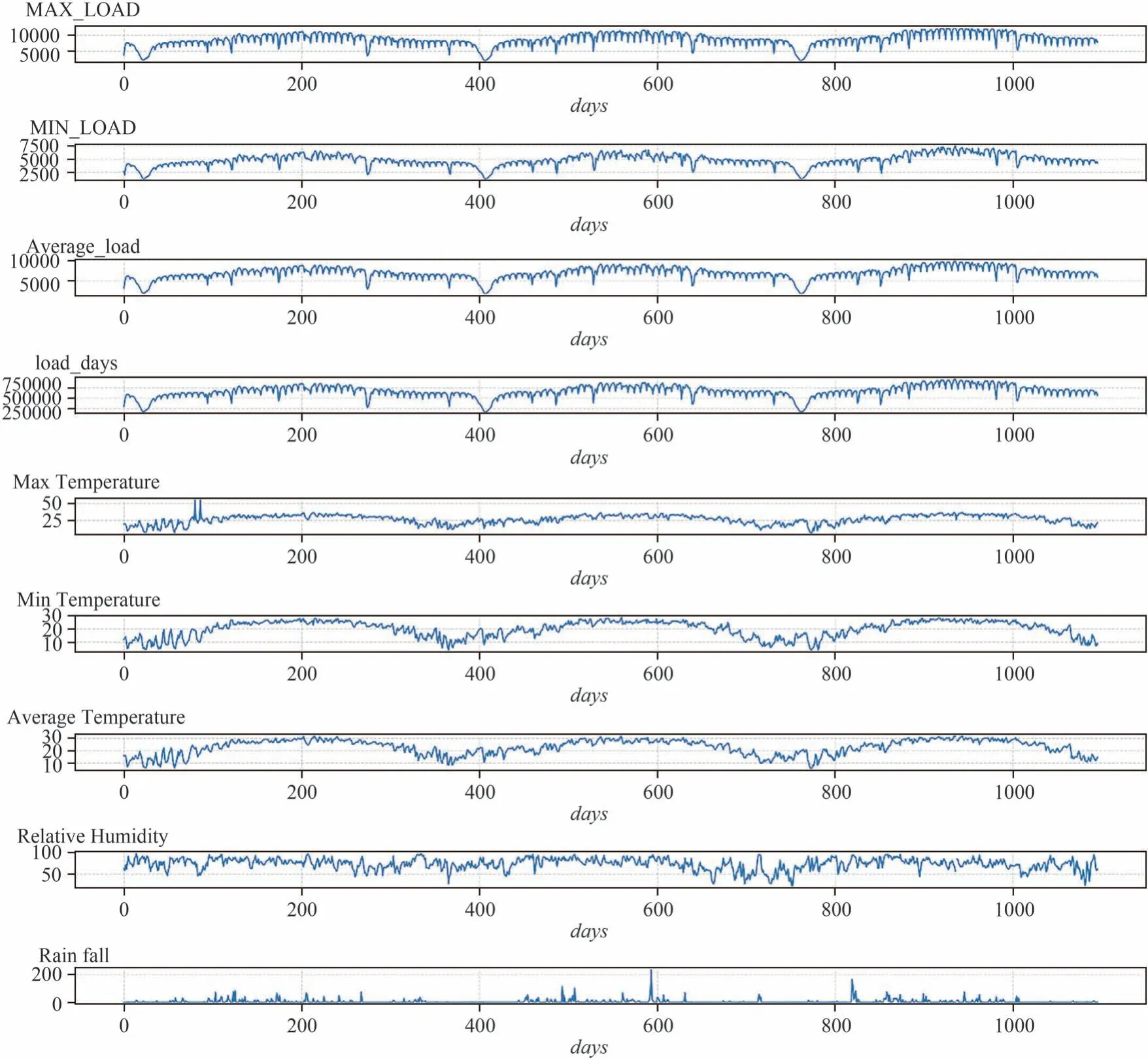
图2 2012年至2014年特征子图Fig.2 Featuresubgraphsfrom 2012 to 2014

相关性最常用的是皮尔森相关系数（Pearson correlation coefficient）.该系数是用来反映两个变量线性相关程度的统计量，使用公式：

公式（1）中，Cov(x，y)是协方差，分母上的两个变量σx、σy表示的是x和y的标准差（standard deviation），皮尔森相关系数范围为［-1，1］，越接近1表明正相关性关系越强，越接近-1表明负相关性关系越强，0则表示两个变量间没有线性关系.线性相关系数|r|及相关程度判定标准：当0＜=|r|＜0.3时，表示低度相关；当0.3＜=|r|＜0.8时，表示中度相关，当0.8＜=|r|＜1时，表示高度相关.

为了进一步说明最高负荷、最低负荷、平均负荷、日负荷、平均温度、最高温度、最低温度、相对湿度、降雨量这9个特征之间的相关度，特通过pandas读取数据，再由数据框调用corr方法，计算了它们之间的皮尔森相关系数，如表1所示.

通过表1可以看出，最高温度、最低温度、平均温度与负荷数据的相关系数大于0.3小于0.8，呈现中相关度，相对湿度、降雨量与负荷数据的相关系数都小于0.3，呈现出低相关性.故在该模型中舍弃特征相对湿度、降雨量，仅将最高负荷、最低负荷、平均负荷、日总负荷、平均温度、最高温度、最低温度7个特征作为模型的输入.

表1 特征之间的相关系数Tab.1 Pearson correlation coefficient amongfeature

1.3 数据预处理

数据预处理是为后期模型的训练做准备，而且数据的预处理也对模型的预测精度有影响.故为了提高电力负荷的预测精度，电力数据需要经过预处理才能将数据喂给预测模型具体预处理的过程，主要包括：根据需要整理合并数据集、数据清洗、数据标准化处理、数据集划分.

（1）数据集合并整理.

找出每一天采样的96个样本中的最大值、最小值，并求出96个样本点的平均值和求和，即得到日最高负荷、日最低负荷、日平均负荷、日总负荷4个特征数据.将这4个维度的特征数据与日平均温度、日最高温度、日最低温度3个维度的特征整合到一起，作为模型的输入特征，将7个维度的特征量数据与每天的96个样本点数据整合到一张数据表中，从而得到一个全新的数据集作为本次实验的数据集（1106行103列）.

（2）数据异常处理.

导入整理好的数据集，由于收集数据值是由人为采集和设备采集，可能会存在缺失值和异常值，而缺失值和异常值又会影响电力负荷预测的精度，故需要对缺失和异常的数据值进行查看并进行处理，用当日样本点的平均值代替异常值和补充缺失值，以避免缺失及异常值对预测结果带来的不良影响.

（3）数据标准化处理.

由于数据尺度太大会影响模型的训练效果并且长短期记忆神经网络预测模型对输入的数据尺度比较敏感，故可用以下公式（2）对异常处理后的数据进行标准化处理，以消除量级量纲的影响提高预测模型精确度，简化计算，提高模型的收敛速度.

公式（2）中x是原始电力负荷数据，xmean为原始电力负荷数据的平均值，xstd为原始电力负荷数据的方差，xnorm为标准化后的标准电力负荷值，其实质是将原始电荷数据转化为符合均值为0，标准差为1的标准正态分布的新负荷数据.经过标准化处理后的电力负荷数据，在不改变原始电力负荷变化趋势的情况下缩小了电力负荷数据尺度.

（4）将数据集划分为训练集和测试集.

预处理后的数据集总共有1106行103列，1106行是指由1106天，103列是日平均负荷、日最高负荷、日最低负荷、日总负荷、日最低温度、日最高温度、日平均温度7个维度特征数据加上每天的96个负荷采集样本数据，数据集划分是按照训练数据集占80%，测试数据集占20%来进行划分的.x_train取的是数据集的前884行的特征数据，y_train取的是前884行的每天的96个采集样本数据.x_test取的是数据集的后222行特征数据，y_test取的是后222行的每天的96个采集样本数据.

2 基于改进的AM-LSTM模型的短期电力负荷预测

2.1 改进的AM-LSTM模型

2.1.1 改进的LSTM单元

激活函数的作用是使神经网络模型的线性改为非线性.若没有激活函数，则无论神经网络有多少层，输出与输入都将呈现出线性关系.即隐藏层失去了其作用，没有激活函数的每层都相当于矩阵相乘，由此可见激活函数对长短期记忆神经网络（LSTM）的影响.为了更充分地发挥隐含层的作用，更好地适应和学习非线性关系的电力负荷数据，将LSTM单元中的激活函数进行了改进，如图3中红圈中的激活函数Tanh，将Tanh激活函数改进成了基于Tanh、Sigmoid、Relu的加权激活函数组，具体展现如图4所示.

根据图3-图4，其中σ为sigmoid函数，LSTM改进后，LSTM单元当前的输出值st公式为公式（3），展示如下：

图3 LSTM单元内部结构图Fig.3 Internal structurediagramof LSTMunit

图4 改进后的LSTM单元内部结构图Fig.4 Internal structure diagram of improved LSTM unit

其中Wi为权重矩阵，ct为当前时刻的单元状态，ot输出门的输出值，st为改进的LSTM单元当前的输出值，T为矩阵转置.

2.1.2 改进的AM-LSTM模型

在对时间序列数据进行处理的时候，会通过计算得到序列中各个元素的特征，如果需要在序列数据上进行信息提取时，需要关注整个序列的特征，而简单地将各个元素的特征相加或者是说求平均，则会导致模型的输入序列中每一个元素对于模型的输出序列中的每一个元素的影响力相同.因此，本文在模型中引入attention机制，加入注意力机制的改进的LSTM模型称为改进的AM-LSTM模型.改进的AM-LSTM模型用到了序列到序列的框架，其中编码器（Encoder）部分采用的改进的LSTM单元，解码器（Decoder）部分也采用的改进的LSTM单元，具体框架如图5所示.

Lut对照品，批号111520-201605，质量分数99.6%，中国食品药品检定研究院；香叶木素对照品，批号P0587，质量分数99.4%，上海源叶生物科技有限公司；聚乙烯吡咯烷酮（PVK 30），批号25000240379，Ashland公司；卵磷脂，批号PC-98T，辅必成上海医药科技有限公司；其他试剂均为分 析纯。

图5 改进的AM-LSTM模型Fig.5 Improved AM-LSTM model

初始向量x1，x2，...，xn是输入特征向量，本次训练数据集有最高温度、最低温度、平均温度、最高负荷、最平负荷、平局负荷、日总负荷7个特征向量，故用到7个改进的LSTM单元，7个输入特征向量经过改进的LSTM单元进行编码，输出固定长度的向量通过注意力机制（Attentional Mechanism）输出注意力机制的上下文C1，C2，…..，Ct，输出的注意力机制上下文通过解码层，输出预测结果o1，o2，...on.

在基于注意力机制的网络模型中，它是首先计算一组注意力权重，通过乘上编码器输出的向量来创建权重的组合.计算结果应该包含有关输入序列特定部分的信息，从而帮助解码器选择正确的表征进行输出.因此，解码器（Decode）可以使用编码器（Encode）序列的不同部分作为context直到解码完所有序列.

注意力机制在解码阶段的每个时间步长t计算一个向量ct和一个输出结果ot， 计算公式为：

其中hj是输入向量xj的隐藏层状态，atj是hj预测ot的权重.向量ct也被称作为期望注意力向量，通常可以被softmax函数计算出来，公式为：

其中attentionScore函数可以选择解码部分的隐藏状态和编码的隐藏状态来计算出一个用于计算权重的分数.

3 实验与结果分析

3.1 模型评估指标

模型评估指标是用来评价模型预测误差精度大小的预测性能的评价标准尺度，本次实验采用了平均绝对误差MAE（Mean Absolute Error）、均方根误差RMSE（Root Mean Squared Error）、对称平均绝对百分比误差（Symmetric Mean Absolute Percentage Error）、决定系数R2（R-Square）等来评估预测模型的预测精度［15-16］.具体如下：

假设y=[y1，y2，y3，…，yn]，其中n=1，2，3...4，为未来4天的真实值.y^=[y^1，y^2，y^3，…，y^n]为未来4天的预测值，其中n=1，2，3...4.m是测试样本数量，则本次回归模型的评估指标的公式分别可表达为：

均方绝对误差（MAE）：

均方根误差（RMSE）：

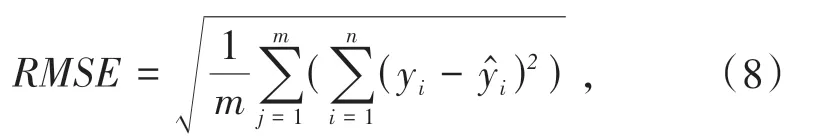
决定系数（Coefficient of Determination，R2）：

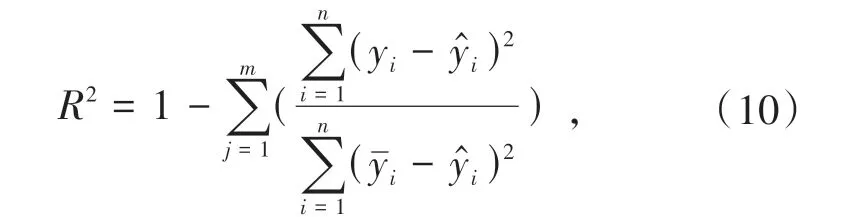
公式（7）中yˉi表示的是真实值的第i天的平均值，其中MAE、RMSE、SMAPE的范围均为［0，+∞），当预测值等于真实值时等于0，即理想模型；误差越大则模型预测精度越低；而R-Squared的范围为［0，1］，如果R-Squared=0则说明模型拟合效果特别差，如果R-Squared=1则说明模型无错误，一般来说，RSquared的值越大，表示模型拟合效果越好，预测值与真实值越接近，模型预测精度越高.

3.2 模型训练步骤

本次实验采用改进的长短期记忆网络模型，用3年的电力数据进行测试训练，训练好的模型用最近1年的电力负荷数据来预测未来4天的电力负荷，其主要步骤如图6所示.

图6 改进的AM-LSTM算法预测模型流程图Fig.6 Flow chart of improved AM-LSTMalgorithmprediction model

输入：最高温度、最低温度、平均温度、日最高负荷、日最低负荷、日平均负荷、日负荷7个特征向量及96个负荷样本向量.其中7个特征作为x_train，96个采集样本向量作为y_train.

输出：未来4天的电力负荷预测值，每天的负荷预测值数据包含96（24h/15min=96）个时间点的负荷预测值.

第1步，确定模型的输入.将收集好的历史数据作为模型的最主要输入量，同时为了提高模型的预测准确率，需要将一些可能影响负荷变化规律的外在因素进行充分考虑.对可能影响负荷变化规律的一些外在因素日最高温度、日最低温度、日平均温度、相对湿度、降雨量与电力负荷数据（日最高负荷、日最低负荷、日平均负荷、日总负荷）进行相关性分析，找出相关性大并有助于提高模型预测精度的影响因素，将其数据看作特征和电力负荷数据一起作为模型的特征输入.

第2步，数据预处理.输入的数据若不经过预处理而直接喂给模型用于训练，这会致使训练的结果不佳，因此模型的输入数据在输入模型前，一定要经过预处理.预处理过程主要包括：对缺失等异常数据进行补充、对数据进行标准化处理、将数据分为训练集和测试集等.

第3步，预处理后的数据喂给模型对模型进行训练，训练后的模型会输出预测的负荷数剧，将预测的数据和真实数据进行对比，评估观测模型的预测效果.

第4步，如果预测效果达不到要求，就修改调整模型的参数进行再次训练预测结果与前一次训练的预测结果对比，直到模型的预测结果达到要求为止.

3.3 模型的预测结果

为了能体现出改进的AM-LSTM模型的预测精度更高，本次实验对LSTM模型、AM-LSTM模型结合电力负荷数据也进行了训练并预测，结合改进前的LSTM、改进的AM-LSTM模型的预测结果进行对比分析.LSTM模型对未来4天的电力负荷预测结果（真实值与预测值的对比）如图7～10所示.

图7 LSTM模型预测第1天的结果Fig.7 Predicted resultsof first day using LSTMmodel

图8 LSTM模型预测第2天的结果Fig.8 Predicted results of second day using LSTMmodel

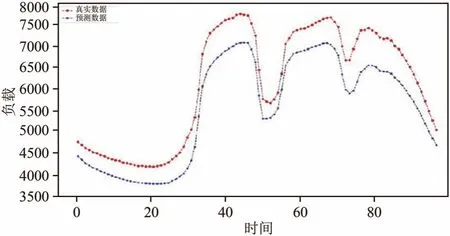
图9 LSTM模型预测第3天的结果Fig.9 Predicted results of third day using LSTM model s

图10 LSTM模型预测第4天的结果Fig.10 Predicted resultsof fourth day using LSTMmodels

为了改进的AM-LSTM模型对未来4天电力负荷预测的预测结果（每天隔15分钟一个电力负荷值，共由96个电力负荷值）如图11～14：

图11 改进的AM-LSTM模型预测第1天的结果Fig.11 Predicted results of first day using Improved AM-LSTM model

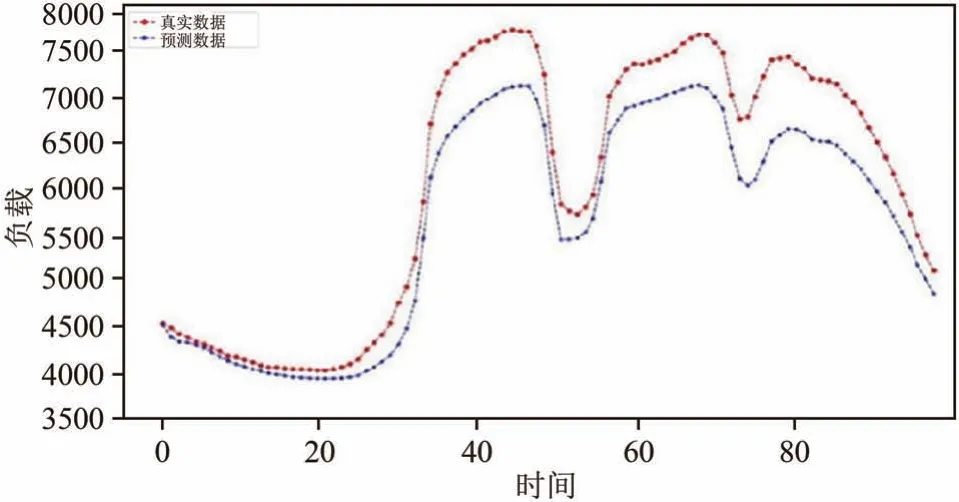
图12 改进的AM-LSTM模型预测第2天的结果Fig.12 Predicted resultsof second day using Improved AM-LSTMmodel

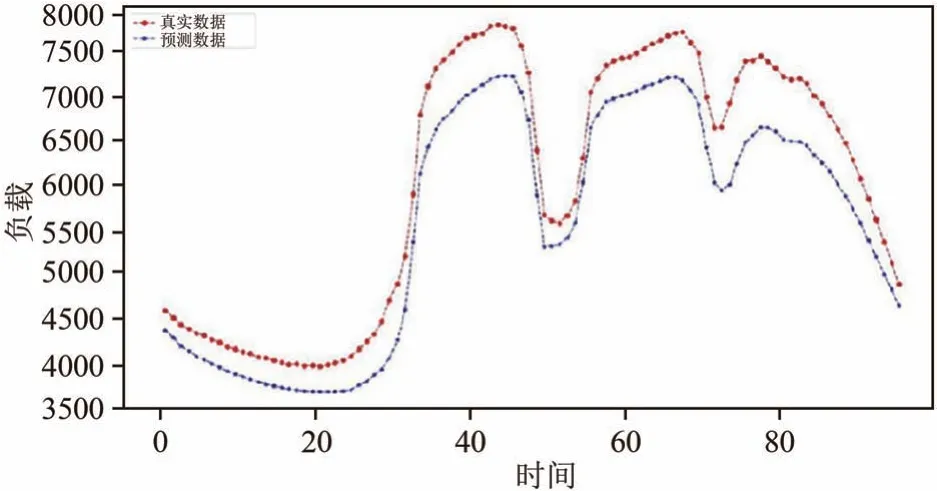
图13 改进的AM-LSTM模型预测第3天的结果Fig.13 Predicted resultsof third day using Improved AM-LSTMmodel s

从图11-图14中，可以看出改进的AM-LSTM模型能够更好地预测出未来4天的电力负荷值，拟合效果优于改进的AM-LSTM.为了更值观地看到改进的AM-LSTM模型的性能，根据模型的评估指标公式计算了模型的评估指标，如表2所示.

图14 改进的AM-LSTM模型预测第4天的结果Fig.14 Predicted resultsof fourth day using Improved AM-LSTMmodel

表2 改进的AM-LSTM模型评估指标Tab.2 Improved AM-LSTM model evaluation index

4 小结

本文主要提出了改进的AM-LSTM模型，并结合短期电力负荷数据验证并证明了改进的AM-LSTM短期电力负荷预测模型的预测精度比未改进的AMLSTM精度更高，添加了注意力机制的LSTM模型比LSTM模型的预测精度高.在提出改进的AM-LSTM模型前还做了一些数据处理的工作，主要包括：对电力负荷数据进行了分析，得出电力负荷数据呈现周期性、连续性的特性；分析了外在天气因素日最高温度、日平均温度、日最低温度、相对湿度、降雨量与最高负荷、最低负荷、平均负荷、日总负荷之间的相关性，并选取了相关性高的天气因素数据与负荷数据一起作为输入特征；将数据特征数据与每天采集的96个样本数据整合在一起，对整合后的数据进行清洗、标准化、划分训练集和测试集.