基于题感培养的初中数学单元复习课教学实践

⦿江苏省靖江市滨江学校 常静锋

如何培养学生的题感已经成为提高解题教学质量的一个热门话题.在初中数学优质解题教学的实践研究中，笔者曾对其理论建构进行了初步探讨，随着探究的不断深入，对优质解题教学的价值取向更加明晰：优质的解题教学需要践行核心素养培育的理念，秉持为思维而教的教学观，在教学的过程中凸显题感的培育，展现优效教学的主张，追求高效优质的效果.这是一种低耗型、可持续的教学形态，在单元复习课中的体现尤为明显.可见，解题教学应着力培养学生的创新素养和题感.在此价值的引领下，笔者通过具体教学实践，重点探讨解题教学中题感的培养策略.

1 放飞思维，成为审题的“主人”

解题的第一步自然是审题，我们都知道审好题是解好题的关键所在.而当前解题教学中，有些学生不喜动脑，习惯于教师“喂养”，思维的启迪通常源于教师的一步步提示，更有甚者等着教师直接讲解，自己更愿意充当一个听众；也有些教师沿袭传统教学中师道尊严的观念，在教学中捍卫自己的绝对权威，用自己的讲解去代替学生的思考，常常将学生的灵感与想法扼杀于摇篮之中.试问，如此教学之下，学生的题感从何而来？自然，这样一来学生自身的思维能力逐步弱化，当需要独立解题时，少了教师的提示，思维就无法打开，更不要说本该有的题感.事实上，解题的过程就是让学生通过各种选择，如知识、方法、思想，进行思维拓展，并形成题感的过程.如果略过这个环节，那么如何培养题感，如何学会解题，又如何谈能力的提升？笔者认为可以从以下方面着手.

(1)给足“想”的时空

出示问题之后，教师首先要做的并非分析和讲解，而是需要给足学生“想”的时间和空间，让学生有足够的时间去厘清题意，探寻思路.在这个过程中，教师也并非完全地冷眼旁观，可以这样激励和引导学生：“分析条件你想到了什么？分析问题你又想到了什么？多朝着与条件、问题有关的知识方法去想，或许你会有更多的发现.”由于习惯的养成需要经历“强制—认同—自觉”的过程，经常性地给予学生这样的提示和启发，可以强化学生的心智，促进学生养成深入思考的习惯，对知识的融合、知识的发生和发展都有帮助.

(2)多给“画”的机会

数形结合是解决数学问题的重要思想方法，而目前学生通过数形结合解决问题的观念落实得并不理想.因此，厘清题意之后，可在脑中“画”出单元基本结构，“画”是促进学生进行直观思考的根本方法.教师应多给学生“画”的机会，助力学生审好题，促进题感的形成.

2 借题发挥，逐步孕育题感

教师教学不仅需要变化，而且要会变，让学生对这些大变化和小变化产生兴趣.解题教学也需做到善变，要会通过对例习题的挖掘进行改编，以启发学生思维，发展学生思维能力.因此，借题发挥，通过“小题大做”来拓展延伸是孕育题感的关键一步.

(1)一题多解

一题多解，就是通过一个典型问题，启发学生从不同角度，运用不同思路、方法去分析和解答的思维训练活动.这样的借题发挥训练，可以让学生的思路越发宽广，逐步形成题感，逐步提升解题能力.这里需要注意的是，在通过一题多解培养题感时，不能一味追求解法的数量，而应通过对比各种方法的优劣性去渗透解题的思想方法.

例1已知O为△ABC中线AD的中点，连结BO并延长后与AC相交于点E,求AE∶EC.

方法1：作平行线后借助于平行线分线段成比例的定理解题(仅列举其中一种解法).

如图1，过点D作DF∥BE且与AC相交于点F.

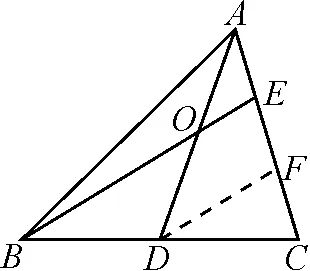
图1

因为DF∥BE，且点D平分BC，所以CF=FE.

同理，可得AE=EF.

方法2：作平行线后借助于相似三角形预备定理解题(仅列举其中一种解法).

如图2，过点D作DF∥AC且与BE相交于点F.

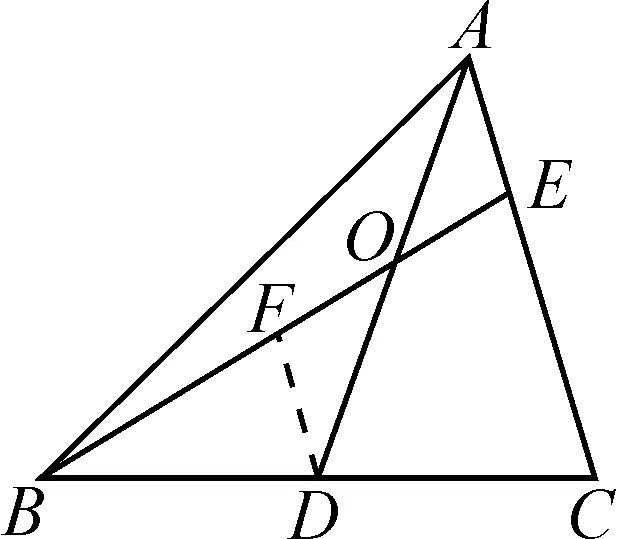
图2

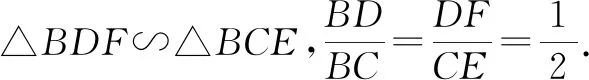
方法3：通过引入参数，借助于代数法(仅列举其中一种解法)解题.

如图3，过点O作OF∥AC与BC相交于点F.

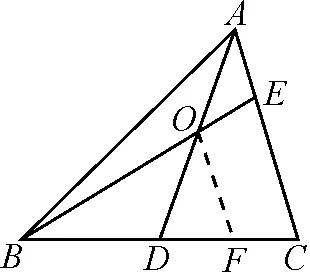
图3

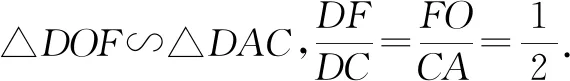
设DF=x，OF=y，则BF=3x，BC=4x,AC=2y.

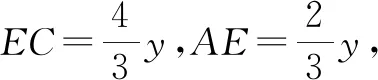
方法4：借助面积求线段比.

如图4，连接DE.

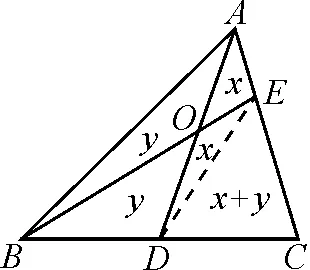
图4

因为点O是AD中点，所以S△AOE=S△DOE，S△AOB=S△DOB，S△BDE=S△CDE.

设S△AOE=x，S△AOB=y，则S△BDE=S△CDE=x+y.

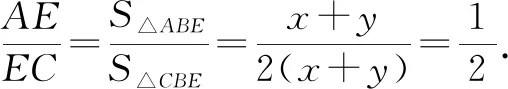
从本例中可以看出，典型问题蕴含丰富的知识、方法和解题技巧，各种不同方法的纵横交错使得显性的知识训练越发到位，达到了对知识技能的最优整合，同时通过最优方法的探寻，很好地培养了学生的探究精神、创新意识和题感.

3 一题多变

一题多变，就是通过对原题的加工和引申，打开学生的思路，使其积极投入到问题的分析中去.通过变题让学生去联想、去深思、去探究，不仅锻炼学生的审题和解题能力，而且还提高了学生的学习效率，更重要的是通过解题让学生获得良好的解题感觉，促进题感的提升.

例2当等腰三角形的顶角是36°时则具有以下特性：经过它的某一顶点的一条射线可将其分为两个小的等腰三角形.请解答：

如图5，已知△ABC，∠A=36°，AB=AC，射线BD平分∠ABC并与AC相交于点D.

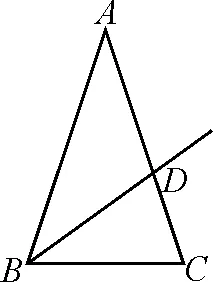
图5

证明：△DAB和△BCD均为等腰三角形.

变式1请在图6和图7的两个三角形中各画一条射线，分别将原三角形分为两个小等腰三角形，再分别将画出的小等腰三角形的两个底角的度数标出来.

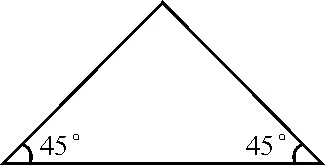
图6

图7

变式2试着画出2个具有该特性(例2给出的特性)三角形的示意图，再将每个小等腰三角形的各个内角度数标出来.(注明：2个三角形不可相似，也不可是等腰或直角三角形.)

综上分析可看出，一道高立意的数学问题，能让学生经历深入探究的历程，让手、口、脑都“动”起来，充分调动学习的潜力，获得解决问题的灵感.更重要的是，学生在问题中探究，在探究中反思，在反思中发现，在发现中成长，最终提高了解决问题的能力.

4 关注“双基”，确保题感的提升

解题作为考查学生学习效果和学习能力的有效途径，对学生的“双基”提出了较高的要求.想要高效解题，就需要有价值且相对连贯的基础知识和相对稳定的基本技能.这就需要教师重新审视教学中的“双基”训练，是否达到让学生自主建构新知的作用，是否实现为培养题感增效的效能.

当然，每个学生都是独立的个体，学习也是自己的事情，教师身处其中也只是一个引导者.这就需要学生具有较强的自主学习能力，才能通过发现式学习、探究式学习、研究性学习和自主学习等多种方式，去习得知识，进而不断生长智慧与能力，真正意义上提升解题能力.

“双基”是学习的核心，是培养数学素养的基石，是形成与发展解题能力的基本策略[3].只有不断优化和提升“双基”训练的质量，才能让学生的知识更稳定、思维更活跃、题感更丰富、学习更自信.

总之，作为教师，我们不仅需要关注到学生审题能力的拔节，还需关注到孕育题感的借题发挥策略的有效应用，更重要的是需要始终关注到对学生“双基”的训练，这样一来，才能让学生题感的提升水到渠成，从而为解决问题能力的进阶做好充分的准备.长此以往，学生的创造性思维能力自然得到提升，数学素养自然得以发展，利于学生的终身发展，这样的初中数学优质解题教学方式应是我们不断追求的.