漏磁法无损检测技术优化与检测效果比较
2023-01-05林益遐
林益遐
(秦皇岛技师学院,河北 秦皇岛 066000)
漏磁法无损检测主要应用于钢轨、钢丝绳、炮管、罐体等铁磁材料表面缺陷以及内部缺陷检测领域,并取得了良好的应用效果。现阶段,铁磁材料磁场分布计算问题仍然没有得到很好地分析和解决,在均匀外磁场磁化条件下,基于有限元法和磁荷法,提出铁磁材料表面缺陷磁场分布法。但该方法仅仅能获得基于椭圆、矩形等铁磁表面的缺陷漏磁分布初步结果,无法满足实际检测相关要求,出现这一现象的原因主要集中2点:(1)在实际检测领域,铁磁材料内部磁场分布呈现出突出的非均匀特性;(2)在实际检测领域,材料磁化处理通常呈现出非均匀状态,导致磁导率会随着磁场强度变化呈现出明显的变化。因此,加强对铁磁材料磁场分布的合理化计算显得尤为重要。
1 漏磁法无损检测理论基础与技术
电荷主要用于对电场源的产生,而电荷空间位置通常表现出固定不变的状态;同时,在时间的不断推移下,电量所对应的电荷并没有形成相应的电场,该电场被称为“静电场”。另外,一旦电荷出现定向移动,电路会瞬间产生相应的电流,当电流处于稳恒状态时,则会出现静磁场,电流和磁场两者之间相互独立,互不影响。但是,在时间不断推移下,一旦电场出现不同程度的变化,电场会直接转换为磁场。当时变电场和时变磁场出现相互转换时,会形成时变电磁场。从电磁学的基本理论出发,用磁畴解释了铁磁性物质的磁化过程,介绍了恒定磁场的边界条件。通过磁阻最小原理解释了漏磁检测技术的原理,对漏磁检测的等效磁路、提离效应和速度效应进行研究,并且分析了使用脉冲方波激励的优势。
1.1 电磁法理论基础
1.1.1铁磁性材料的磁化过程
磁化现象,主要是指通过设置相应的磁场,确保磁性材料 表现出明显的磁特性。在大自然界中,磁性材料主要包含3种:顺磁性材料、反磁性材料和抗磁性材料。磁性主要是借助电子内部的磁矩性能所获得的,铁作为一种重要的顺磁性材料,内部经常会自发性地出现磁化现象,该现象被称为磁畴。在微观层面上,可以借助磁畴理论知识,科学、有效地解释铁磁化过程,然后,利用磁化曲线,生动、形象地描述磁化特性。当铁磁材料在实际使用时,并没有出现被磁化现象,需要采用随机排列的方式 ,对铁磁材料内部磁畴进行排序,磁矩会呈现出相互抵消的状态,导致铁磁材料并不会对外显示出明显的磁性。当外部磁场施加到一定值后,磁畴会自动沿着所设置好的磁场方向进行自动排序,从而形成一定强度的附加磁场。对于铁磁材料而言,其磁化过程主要包含4个阶段:(1)起始磁化阶段。在这一阶段中,由于受磁畴惯性的影响,当外磁场强度不断增加时 ,铁磁材料内部磁感应强度会呈现出缓慢上升的趋势,导致畴壁迁移现象变得越来越突出,起始磁化阶段总体上呈现出一定的可逆性。(2)直线阶段。在这一阶段中,铁磁材料磁感应强度会随着磁场强度的不断增加而呈现出直线上升的趋势,出现这一现象的根本原因是在外磁场的影响下,磁畴方向与磁场强度方向越来越接近,这一阶段通常表现出一定不可逆性。(3)饱和阶段。在该阶段中,磁畴方向始终与外磁场方向保持一致,如果不断地增加磁场强度值,磁感应强度处于饱和状态,不会继续增加,曲线整体呈现出平缓状态。在外磁场的影响下,铁磁材料会被磁化处理,并转变为饱和状态,此时,如果将外磁场撤掉后,铁磁材料并没有出现退磁现象,而是呈现出另外一种变化状态。当外磁场强度降到最低 时,铁磁材料 所对应的 磁感应强度并不会立马消失,而是存在一个临界值,该临界值被称为“剩磁感应强度” ;同时,铁磁材料磁感应强度所呈现出的变化状态总是滞后于磁场强度变化状态,这就是所谓的“磁滞现象”。如果对整个磁场施加一个反向磁场力,铁磁材料磁感应强度会在第一时间内立马消失,此时,可以将反向磁场强度称为“矫顽力”,从而形成相应的磁滞回线。该曲线沿着原点呈现出中心对称的状态,确保整个磁滞损耗与曲线围绕面积两者之间呈现出正比状态。
1.1.2恒定磁场的边界条件
对于铁磁材料而言,其磁场在同一介质中分布表现出一定的均匀性。当磁场在不同介质中进行传播时,不同介质的分界处会呈现出一定的不连续现象。另外,铁磁材料内部磁场强度会与各个分界面之间呈现出一定的平行且密集的状态, 当磁场穿过铁磁材料后,会与铁磁材料表面相垂直。
1.2 漏磁法无损检测技术
1.2.1漏磁检测技术原理
漏磁检测主要是在磁粉检测原理的基础上提出的,通过利用磁阻最小值原理,采用外加磁场的方式,对整个样本进行磁化处理,确保其始终处于一定的饱和状态。当样本存在缺陷时,由于其内部磁阻增大,导致一部分磁场穿出样本表面,形成可以检测的漏磁场,从而发现缺陷的存在。其检测对象一般为导磁材料,漏磁检查原理图如图1所示。

图1 漏磁检查原理图Fig.1 Schematic diagram of magnetic flux leakage inspection
由于铁磁性材料的相对磁导率远大于空气,如果样本表面平滑,那几乎所有磁力线均在样本内流过,漏磁场很微弱,一旦样本出现一定的缺陷问题,由于样本所对应的磁导率比较小,导致磁阻变得越来越大,此时,缺陷处磁场变得越来越突变。在样本缺陷处 ,难以借助漏磁场对其进行处理,因此,漏磁场会在样本表面处出现少量泄露,从而形成相应的漏磁场,该漏磁场表现出一定的可测量性。缺陷处漏磁场的大小及其分布情况与缺陷的几何参数密切相关,使用磁场传感器对漏磁场进行测量,寻找与缺陷相关的特征量,从而可以反演评估缺陷参数。当探头从左向右扫过缺陷时,磁场传感器采集到的漏磁场信号可以正交分解为水平分量Bx和垂直分量By,它们随着检测位置x的变化如图2所示,零位置为缺陷正中心。Bx在缺陷正中心处的幅值最大,由于缺陷边界附近磁场畸变导致在缺陷边角附近存在微小的波谷;By在缺陷中心处幅值为零,并在缺陷两侧各有一个波峰和波谷。
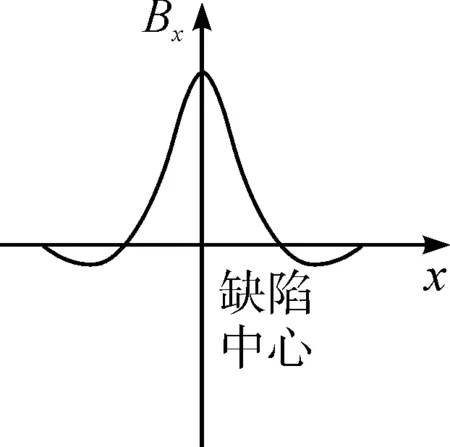
(a)水平分量Bx

(b)垂直分量By图2 缺陷处漏磁场分析Fig.2 Analysis of leakage magnetic field at defect
1.2.2磁路分析
在许多实际问题中,计算主磁通Φ或是某处的磁感应强度B是很有必要的。但在一般情况下,精确求得磁场分布比较困难,所以通过借鉴电路分析的方法,采用磁路近似分析这些问题。
1.2.3提离效应分析
在漏磁检测中,提离是不可避免的。当提离值很小的情况下,忽略磁场的边缘效应。假设B0、B1分别为气隙和磁芯中的磁感应强度,由于磁场垂直于磁芯和空气隙交界面,根据磁场边界条件有B0=B1,得到以下公式:
式中:μr1为磁芯的相对磁导率,其值远大于1,故H0≫H1,提离处的磁场强度很大。如果提离值过大,则气隙中会消耗很大部分磁动势,导致样本内分得的磁势减小,不利于样本的磁化。并且随着提离值增大,缺陷处漏磁场减小,不利于磁场传感器采集漏磁场信号,所以漏磁检测中应尽可能地减小探头的提离值。
1.2.4速度效应分析
当探头与被测样本之间存在相对运动时,原理类似于交流激励。尤其是在探头运动速度很快的情况下,前一个区域还未完全磁化,探头就已经运动到下一个区域,在铁磁性材料中产生感应涡流,影响缺陷处磁场的分布情况。
1.2.5脉冲漏磁检测技术
相比于直流激励与交流激励而言,脉冲方波信号具有更加丰富的频谱信息,可以反映出不同深度的缺陷情况[4-7]。在脉冲方波信号的上升沿和下降沿处,产生瞬态变化的磁场,根据法拉第电磁感应定律,当闭合回路中磁通量发生变化,导体将会感应出电动势,形成电流阻碍磁通的变化。感生涡流具有趋肤效应,导体表面上的涡流密度要远大于导体内部,当电流密度下降到表面的1/e时的深度称为涡流的渗透深度,其表达式
式中:δ为渗透深度;f为激励频率;μ为材料磁导率;σ为材料电导率。可见在高频激励、材料高磁导率或高电导率的情况下,涡流的渗透深度会显著降低,浅层缺陷对涡流的影响较大,而深层缺陷对涡流影响则较小。
1.3 漏磁检测有限元仿真分析
1.3.1有限元分析法
解析法和数值法是求解漏磁场分布的2种主要方法。使用解析法求电磁场方程组的解是非常困难的,仅适用于几种特殊情况,如采用磁偶极子模型对一些简单的点缺陷、矩形截面缺陷给出解析解。对于一些复杂形状的缺陷,因为无法确定磁偶极子的分布情况,所以引入数值法中的有限元分析法对这类问题进行近似求解。
20世纪50年代,为了研究飞机结构静、动态特性,适用于计算机处理的有限元分析(FEA)方法应运而生,之后便很快应用于求解热传导、电磁场、流体力学等问题。有限元法的主要原理是将所要求解的连续区域离散为若干个单元,这些单元体便称为有限元。各个有限元之间以节点连接,在每个有限元内假设一些简单函数对该区域复杂的解析表达式近似拟合,最后把所有区域联合起来,得到符合整个求解域的近似解,从而把一个连续无自由度的问题转变为离散有自由度的问题。
常用的有限元分析软件有ANSYS、Maxwell、COMSOL Multiphysics等,本文采用Maxwell软件对漏磁检测模型进行仿真分析。
1.3.2激励对漏磁场的影响
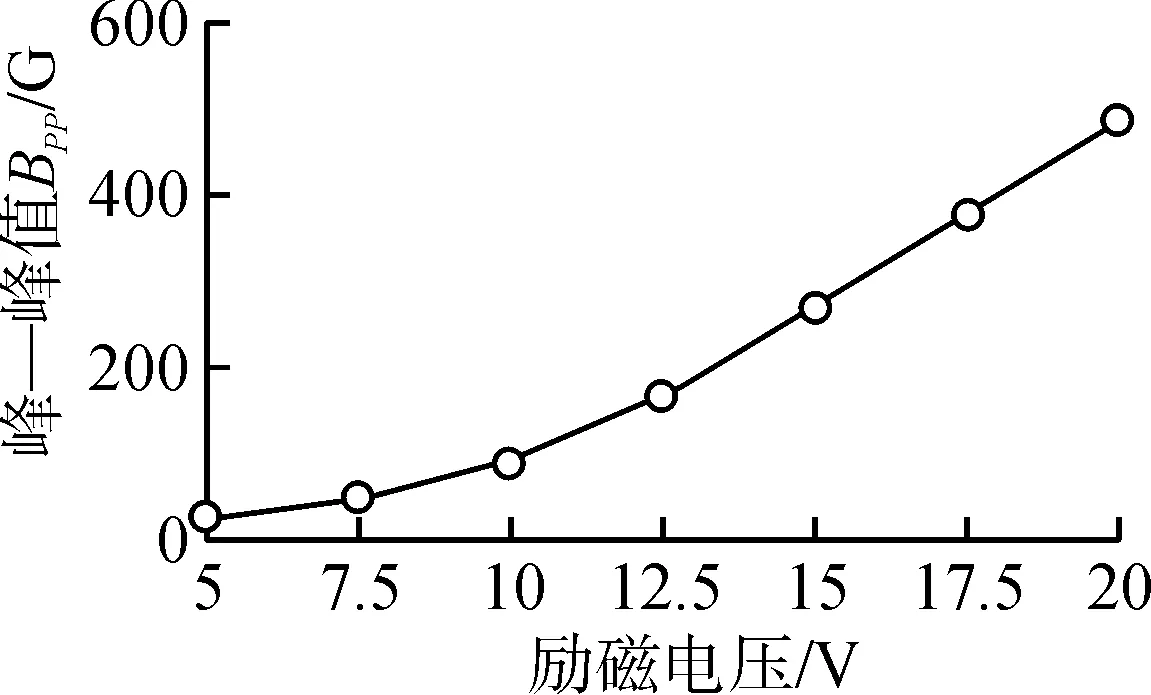
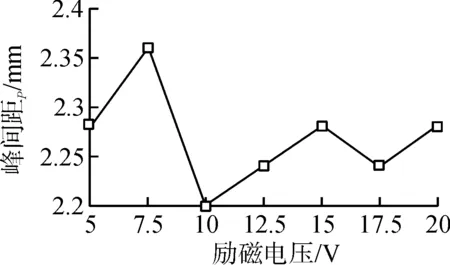
激励的选取对于漏磁检测至关重要。如果激励较小,材料被磁化强度不足,漏磁场较小;如果激励过大,材料进入饱和区后磁感应强度线性变化,电路损耗增大,磁芯容易饱和。根据图3所示的磁化特性曲线和对应的相对磁导率曲线,当H=Hm时材料的磁导率达到最大值,分别从H>Hm和H 图3 5#钢初始磁化曲线Fig.3 Initial magnetization curve of 5# steel 由图3可以看出,通过该区域垂直于磁场方向的横截面的磁通略微增大,因为缺陷空气域的磁导率要远小于材料磁导率,一部分增大的磁通将会绕过缺陷从其附近的材料通过,导致材料中磁场强度增大,磁导率下降,材料磁阻增大,这将会使缺陷附近的漏磁通相对增大。材料中磁场强度小于Hm,类似上述分析,随着材料中磁场强度增大,磁导率上升,磁阻减小,导致更多的磁通在材料内部通过,使缺陷附近的漏磁通相对减小。基于现有模型,改变激励电压从5 V到20 V,间隔2.5 V。随着激励电压增大,垂直方向漏磁场分布呈逐渐变大趋势,峰谷值增大,峰谷处位置几乎保持不变。其特征值Bpp的变化趋势如图4(a)所示,Bpp在激励电压较小时上升缓慢,之后逐渐加快;在激励电压大于15 V后Bpp几乎呈线性增大。这与之前所分析的相吻合,在信号缓慢上升区,材料中的磁场强度小于Hμm,不利于漏磁场的产生;而在线性上升区,材料已经处于近饱和状态,磁场强度大于Hμm,有利于漏磁场的产生。在图4(b)中,Xpp随着励磁电压上升在2.2~2.35 mm内无规律变化,最大变化率为7%,可以认为是仿真误差所引起的变化,判断改变励磁电压只会影响到Bpp的幅值,而对Xpp无明显影响。 (a)峰-峰值 Bpp (b)峰间距xpp图4 漏磁场垂直分量的特征值随激励电压变化图Fig.4 Variation of eigenvalue of vertical component of leakage magnetic field with excitation voltage 为了进一步提高漏磁法无损检测结果的精确性,本文所选用的励磁磁体主要以“U形磁体”为主,其检测装置如图5所示。 图5 检测装置Fig.5 Detection device U形磁体在实际使用期间,所激发的磁场总是呈现出非均匀状态,特别是在磁极附近位置处,其非均匀性特征变得尤为突出;因此,铁磁材料所对应的磁化过程同样也会呈现出非均匀状态。为了实现对铁磁材料内部磁场分布的科学化计算,要根据真空条件,精确地计算出U形磁体所对应的磁场分布结果。为此,相关人员要构建出相应的磁场分布坐标系,并结合磁荷相关理论知识,用H表示磁荷qm内部磁场强度。利用该公式,精确地计算出U形磁体 在xOy(二维平面)上磁场分布情况。 H=Hxi+Hxj 式中:σm为磁极上的面磁荷密度。 铁磁材料在实际磁化期间,其磁导率μ计算公式: 磁导率μ与磁场强度H之间存在显著的非线性关系,对磁感应强度分布结果产生了直接性的影响。为了实现对铁磁材料内部磁场分布结果的精确化计算和分析,需要借助μr与H之间的关系式,根据曲线所具有的独特形状,列出以下函数公式: 式中:a、b、c、n、m均表示待定系数。 在实验曲线中,设置2个点,分别是P1、P2点,并保证这2个点始终位于尝试函数曲线中,并分别确定出a、b、c3个待定系数,即: 表1 几种常用钢种的n、m值Tab.1 n, m values of several commonly used steel grades 在进行计算期间,n和m分别从0.01增加到30,整个步长值达到了0.01。将4种铁磁材料 的实验结果和理论结果进行一一对比,发现通过借助尝试函数,所获得的μr=μr(H)关系式完全符合实验结果。由此可见,尝试函数的应用取得了理想的效果。 以上公式可以精确地计算出H,该H可以直观形象地反映出励磁外场分布情况,由此可以推出计算铁磁材料内部磁感应强度公式: B=μrμ0H 综上所述,本文所用到的U形永磁体在实际磁化期间,根据铁磁材料 特点,重点运用了磁场分布 解析函数表达式,该表达式含有两个参数,分别是磁导率和磁场强度,这两种参数存在明显的依赖关系,该依赖关系被称为“普适函数”,可以适用于多种形状的励磁体,这些研究结果为后期深入地分析和研究非均匀外场和非均匀磁化下的铁磁材料磁场分布计算打下坚实的基础。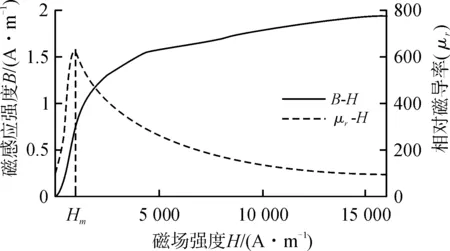
2 U形永磁体的磁场强度环境水质监测分析

3 磁材料的μ-H函数关系与实验结果的比较
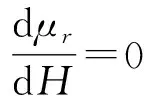

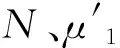
4 材料内部的磁感应强度分布
5 结语
