BP神经网络在水泥土无侧限抗压强度预测中的应用

蔡金轩 孟凡星

（长江大学，湖北 荆州 434023）

0 引言

软土具有高压缩性、低承载力及低抗剪强度等特点。为防止因地基软土而造成不均匀沉降，高层建筑使用水泥土来改善地基条件［1］。影响水泥土强度的因素有很多［2-3］，且存在着复杂的非线性关系。国内外学者提出过经验公式、数值模拟预测方法，但存在结果不精确的局限性。BP神经网络因自身较强的自学习及自适应能力，已广泛应用于拟合、压缩、预测、分类等［4］，其具有较强的映射能力，在抗压强度预测方面表现优异［5-7］。Tang等［8］基于神经网络使用经验模型分析柱屈服性能的影响因素。焦楚杰等［9］分析植生型多孔混凝土抗压强度的主要因素，采用神经网络建立预测模型，对模型预测值及线性回归方程计算值进行对比。宋军伟等［10］利用遗传算法对BP神经网络进行优化，在多元掺和料砂浆28 d抗压强度的预测上表现优异。本研究通过大量室内试验得到不同水泥掺量、水泥种类、水灰比及标号在不同凝期下的抗压强度，并在此基础上采用BP神经网络对水泥土无侧限抗压强度进行预测分析。

1 无侧限抗压强度试验

1.1 试验材料

试验选用典型的淤泥质粉质黏土，参照《土工试验方法标准》［11］进行物理力学性质试验，如表1所示。该试验所用水泥为华新水泥股份有限公司生产的P·O42.5、P·C42.5及M32.5。

1.2 试样制备

参照《水泥土配合比设计规程》［12］对试验的试样搅拌、成型及养护进行统一操作。原状淤泥质土含水量高，初始进行自然风干，之后将风干的土样放置干燥箱进行干燥处理（110℃，不小于8 h），然后将风干后的土样进行粉碎处理，并通过2 mm筛，最后将过筛的土按照试验进行配比。采用机械搅拌，在搅拌结束后20 min内将土样浇筑到模具中，并在振动台上进行振实处理。将试样表面覆膜放入标养室中，进行恒温养护（20℃±2℃、湿度≥95%），24 h后进行脱模，最终将其转至标养室养护至相应龄期。

1.3 试验仪器及方法

试验基于《水泥土配合比设计规程》［12］，选取15%为水泥掺入比基准值，分别设计10%、15%、20%三种水泥掺入比及0.5、0.75、1.0三组水灰比，对凝期为7 d、14 d、28 d的试样进行水泥土无侧限抗压强度试验。采用上海松盾仪器制造有限公司生产的WDW-1电子万能试验机，依据规范要求［11］来调配好相关参数（应力控制为0.15 kN/s），进行试样加载。通过室内试验，获得不同水泥型号、水泥掺入量、水灰比在不同凝期下的抗压强度指标，见表2。

2 神经网络基本理论

2.1 神经网络基本理论

BP神经网络全称为误差反向传播神经网络，其属于多层前向型网络，能以任意精度逼近任何非线性函数［13］，采用BP神经网络对水泥土单轴抗压强度进行预测时，要选取适合的输入特征。当水泥型号相同时，水泥土强度随凝期的增长而逐渐增大，随着水泥掺入量的增加，水泥土单轴抗压强度得到提高［14-16］。研究发现，水灰比对水泥土强度有较大的影响［17］，因此选取水泥种类、标号、凝期、水灰比、水泥掺入量作为预测水泥土强度模型的输入特征。神经网络数据来源室内无侧限抗压强度试验的135个试样。考虑到试验水泥种类不同，将P·O42.5水泥赋值为1、P·C42.5水泥赋值为2、M32.5水泥赋值为3，根据水泥标号不同，将标号42.5赋值为4.25、标号32.5赋值为3.25。

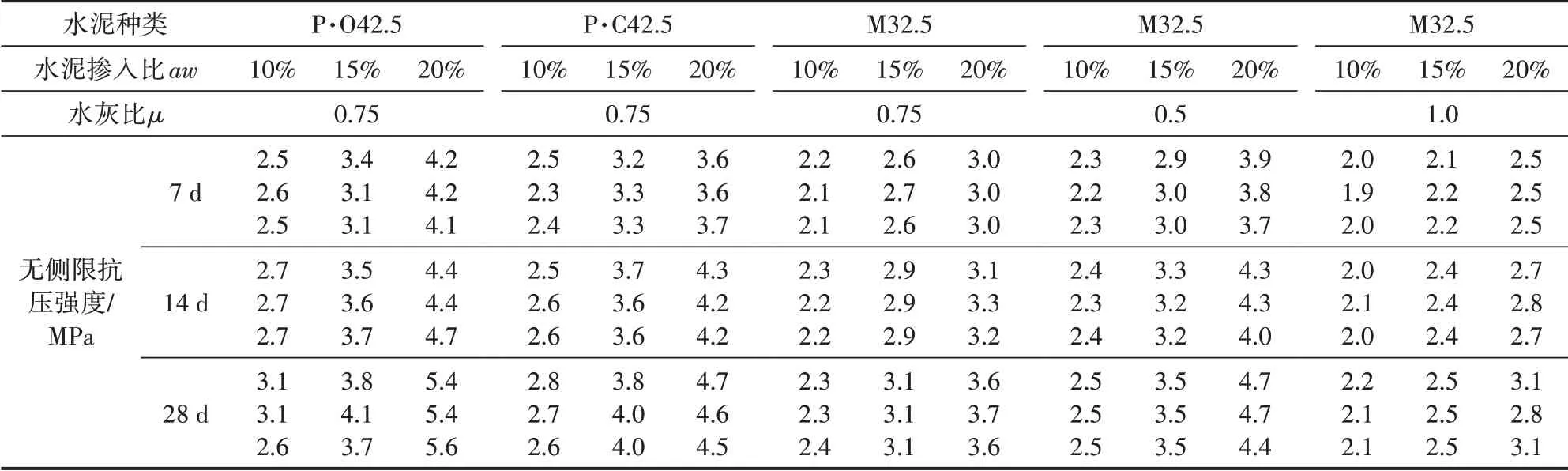
表2 水泥土无侧限抗压强度指标

在神经网络模型预测中，输入层包含种类、标号、掺入量、水灰比、凝期的输入特征。输出层特征选取为试样的抗压强度，选用log-sigmoid函数作为输入层与输出层的传输函数，选取tansigmoid作为函数隐含层与输出层的激活函数。

由于传输函数选取的是log-sigmoid函数，见式（1），其本身只能识别0～1的值，函数在［0，1］内曲线变化平缓。因此，在神经网络训练前，对数据进行归一化处理，将数据值控制在该区间内，从而使该函数在此区间变化梯度较大，提高网络收敛速度。数据归一化的方法选最大最小法［18］，见式（2）。

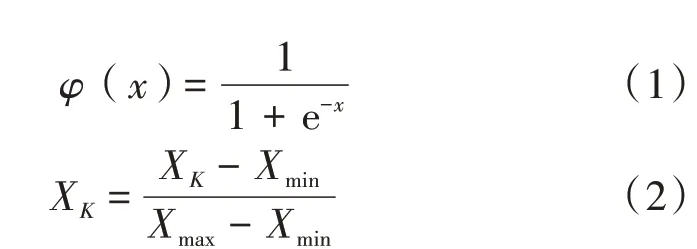
式中：x为向量矩阵的数据；φ（x）为函数传递值；X K为归一化的数；Xmin为数据序列最小数；Xmax为序列最大数。

2.2 BP神经网络模型的建立

在建立模型前，先确定隐含层神经元的个数，隐含层神经元数目的选择是比较复杂的问题，往往根据设计者的经验及多次试错来确定，没有明确的解析式能推导出建立模型所需的神经元个数。关于隐含层神经元的个数确定［4］可参照经验公式（3）。

式中：n1为神经元个数；m为输出神经元个数；n为输入单元数；a为［1，10］内的常数。

本研究的输出神经元个数为1个，输入单元数为5个，则隐含层神经元的个数为［4，13］，最优神经元个数要在该范围通过多次试算才能确定。

在神经网络训练中，训练样本的数目越多，则训练结果越能反映其内在规律，本研究选取的样本总量为135个，软件随机选取95个样本，并将其随机划分为70%的训练样本、15%的测试样本及15%的验证样本，剩余的作为预测指标。选取均方差MSE（Mean Square Error）作为神经网络终止训练的准则，通过M SE来反映神经网络的性能及神经网络的精度。均方差越小，则网络性能越好，精度越高。采用R2来反映训练样本、测试样本、预测样本及总样本的输出与目标间的相关性。

不同神经元个数下试算的M S E值和R值如图1、图2所示。由图1、图2可知，该BP网络结构在为5-8-1时MSE值最小、R值最大，预测的精度较高且比较稳定。因此，用于水泥土强度预测的神经网络，其隐含层神经元为8个。

图1 不同神经元下的MSE值

图2 不同神经元下的R值

2.3 回归及预测结果

图3为BP神经网络模型性能图，该图反映了网络的验证性能，向量的训练在保证误差最小的前提下进行验证，从而防止出现过拟合。由图3可知，该模型最佳验证性能在训练次数为3时取得，且该神经元模型的M S E值为0.001 070 8。

BP神经网络模型的训练阶段如图4所示，误差在第3次训练后重复出现，而在第4次训练停止测试过程没有出现错误。因此，可将该时期的权重当作最终权重。

采用BP神经网络模型对该水泥土强度相关试验数据进行训练，回归结果如图5所示，分别反映训练、验证、测试及总体结果。当R值越接近1，越能表示输出及目标间具有良好的线性关系。该训练样本、验证样本、测试样本及总体样本的R值分别为0.985 81、0.989 75、0.980 04、0.985 51，表明总体上线性回归的结果较好，采用该模型对水泥土强度进行预测结果较为可靠。

在对模型进行反复训练后，神经网络模型能准确预测出水泥土的无侧限抗压强度，得到的水泥土强度预测结果对比见图6。由图6可知，通过神经网络对样本进行训练预测，室内试验数据指标线条与预测线条基本相似，从预测的40个样本可以发现，相对误差最小仅为0.59%，最大为19.54%，对其他结果进行预测，其相对误差均小于20%。因此，在该网络模型条件下输出的参数合理。

图3 BP神经网络模型性能

图4 BP神经网络模型训练状态

图5 BP神经网络模型回归R值

3 结论

本研究采用BP神经网络模型，选用水泥种类、标号、凝期、水灰比、水泥掺量作为输入特征，通过室内试验得到水泥土无侧限抗压强度，并进行训练预测，得到以下结论。①BP神经网络的M S E值约为0.001 152 4，R值约为0.988，该网络模型水泥土无侧限抗压强度能进行较高精度的预测。②网络模型中有90%的数据误差范围在10%以内，表明BP神经网络适用于提取输入特征，能较好地映射水泥土无侧限抗压强度与影响因素间的非线性关系。③采用BP神经网络能快速、准确地预测水泥土无侧限抗压强度，能在一定程度上减小室内试验的工作量，从而节省时间及试验成本。

图6 水泥土抗压强度预测结果对比