真空管道磁浮交通管内波系时空分布特征

胡 啸，邓自刚，*，张银龙，张继旺，张卫华

(1.西南交通大学牵引动力国家重点实验室，成都 610031；2.西南交通大学超高速真空管道磁浮交通研究中心，成都 610031；3.中铁第四勘察设计院集团有限公司，武汉 430063)

0 引言

真空管道磁浮交通将真空管道技术与磁悬浮列车技术相结合，成为了一种新型的地面轨道交通方式。真空管道使列车处于低密度、低气压的运行条件且无外界环境干扰，理论上能够最大限度地减少列车的运行阻力[1]。2013年，美国伊隆·马斯克提出“超级高铁”概念。随后，研发风潮迅速席卷全球，法国、英国、德国、韩国等国家纷纷加入这场科技竞赛。其中，以美国的研究进展最为迅速，美国从事“超级高铁”研发的公司主要包括Virgin Hyperloop One、SpaceX、HTT公 司。2020年11月，Virgin Hyperloop One公司实现首次载人（2人）运行测试。

我国也积极投入到了低真空管道运输系统的研究中。2014年6月，西南交通大学完成并成功调试了真空管道高温超导磁悬浮列车试验系统“Super-Maglev”[2]，开展了真空管道磁浮交通在低速运行时的一系列气动特性实验研究[3]，并且在探索过程中，意外地发现低气压对高温超导磁浮车的悬浮特性也有明显的增益效果[4]。为了进一步提高列车实验速度，2020年西南交通大学开始建设最高时速可达1500 km的多态耦合轨道交通动模型试验平台，目前平台已完成设计-采购-施工（EPC）总包。

低真空管道磁浮交通是超大型复杂系统，其中管道内气动特性直接影响管道建设、维护成本以及车辆运行安全性、稳定性和舒适性，这也成为了近些年来的研究热点。列车气动阻力与系统顶层参数（运行速度、真空度、车/管阻塞比）的关系颇受学者们的关注。研究发现，随着列车速度的增加，列车阻力系数先增大后减小，在Kantrowitz极限附近会出现阻力系数的最大值[5]。列车气动阻力与管内气压[6-7]、阻塞比[8]成线性关系。为了进一步减少空气阻力，降低运行能耗，国内外学者开展了列车外形优化[9-10]和管道结构[11-12]设计相关研究。

此外，列车在管道内运行会产生复杂的波系现象，这些波系的反射、传播、干涉也会恶化列车运行环境，进而对列车运行的安全性、稳定性和舒适性产生影响。周鹏等[13-14]基于二维轴对称车/管模型研究了管道内激波的产生与传播。Niu等[5]也基于二维轴对称车/管模型研究了不同马赫数下波系对管内热压分布的影响，研究结果表明：激波出现在列车的前部和尾部，膨胀波仅出现在尾部，两种波的传播范围随着列车速度的增加而增加。张晓涵等[15]考虑了列车的悬浮高度，建立了二维非轴对称车/管模型，研究了亚声速下管道内激波现象，研究结果表明在尾流区域，激波分布明显不同于对称模型的结果，呈现上下不对称现象。

目前而言，针对管道内波系的研究主要基于二维模型，而列车是具有特殊流线型复杂头型设计的三维模型，列车的三维效应会直接影响管内波系的产生及分布。另外，目前的研究忽略了列车的启动阶段以及管内波系的时变特性。

鉴于此，本文基于IDDES湍流模型及重叠网格技术，研究高温超导磁浮列车在加速启动阶段和匀速阶段管内波系的时变分布特征，为速度为1500 km/h的多态耦合轨道交通动模型试验平台的建设提供参考。

1 数值方法

1.1 列车/管道几何模型

由于目前真空管道交通尚未工程化，因此本文中使用的磁悬浮列车模型根据高速列车的外观和高温超导磁悬浮列车的特点设计。如图1所示，三编组高温超导磁悬浮列车模型包括头车、中间车和尾车，列车的长度L为81.73 m，宽度W为3.37 m，高度H为3.80 m。该列车模型保留了复杂的结构部件，如风挡、低温容器（Cryostat）和悬浮架。悬浮间隙（磁悬浮列车车底（低温容器）和轨道之间的距离）为0.02 m。本文使用的管道模型参考高速铁路的隧道模型，管道净空面积为45 m2。列车/管道的阻塞比为0.2639。轨道采用双Halbach型永磁导轨[2]，双轨之间的间距为2 m。为了减少计算资源的花费，对轨道进行了简化，其尺寸如图1（b）所示。

图1 列车/管道模型及尺寸Fig.1 Train/Tube models and dimensions

1.2 计算区域和边界条件

为了模拟磁悬浮列车在真空管道中运行，采用了STAR-CCM+软件中的重叠网格技术。重叠网格技术已经被证明可以有效地模拟列车在隧道中行驶[16]以及两列车交会时的气动特性[17-18]。总的来说，重叠网格技术是一种区域划分和网格重组的策略。在本研究中，整个计算区域被划分为与磁悬浮列车相连的重叠区域（移动区域）和包括管道与轨道在内的背景区域（静止区域）。为了建立子网格间的信息传递，需要执行两个主要步骤。第一步是“挖洞”，识别计算子区域外的单元。第二步是定义插值算法，用于构建网格耦合的插值公式。

图2展示了计算区域侧视图的边界条件和尺寸。坐标系的原点设置在尾车鼻尖处。x轴的正方向对应于列车运动的反方向。整个计算区域长度为1000 m，即真空管道总长1000 m。在初始时刻（t =0 s），管道入口边界和重叠区域边界之间的距离是45 m。为了模拟一个无限长的真空管道，管道两端（入口和出口）的边界条件被设置为无反射的黎曼边界，称为自由流边界。磁悬浮列车、管道、轨道表面均采用无滑移壁面边界条件，重叠区域边界采用了重叠网格边界条件。磁悬浮列车车尾鼻尖和重叠区域边界之间的距离分别为15 m和65 m。在初始时刻，管道内的静态温度和压力分别为288 K和1013.25 Pa。

图2 初始时刻下计算区域的侧视图示意图(单位：m)Fig.2 Schematic diagram of the computational domain (side view) at t = 0 s（Unit:m）

如图3所示，列车在管道中运行分为两个阶段：加速阶段和匀速阶段。在0～1.04 s，列车以400 m/s2的加速度从0匀加速到416.67 m/s，列车行驶217 m；在1.04～1.75 s，列车保持416.67 m/s的速度匀速行驶295.84 m。列车的运动通过自定义程序实现。

图3 列车速度和运行距离随着时间的变化Fig.3 Variation of the train speed and running distance with time

此外，文献[19]基于二维轴对称车/管模型研究了加速度大小对管内流场结构的影响，结果表明加速度大小对管内流场结构分布特征影响较小。因此为了节约计算资源，本文选取的加速度没有考虑人体的承受能力。

1.3 网格策略

在本研究中，非结构化的混合网格策略（trimmer网格和prism layer网格）用来离散计算域。为了求解壁面边界层处流动，在壁面附着22层prism layer网格，拉伸比为1.2，首层边界层网格厚度为0.2 mm。列车周围的流动是复杂的，尤其是在尾流区域。在本文中，根据Muld等[20]的网格划分策略，结合重叠网格要求，在列车周围和尾流区域使用多级细化加密块，尺寸分别为50、100、200 mm，如图4所示。模型计算网格总数为2638万。这种网格划分方法有效提高了流动复杂区域的求解精度。

1.4 求解方法

使用有限体积法来求解控制方程。为了获得较为准确的计算结果，使用改进的延迟分离涡模拟（IDDES）来解决湍流问题。对于IDDES，它为分离涡模拟（DES）公式提供了一些壁面建模的LES（WMLES）的功能。IDDES被广泛用于高速列车的气动特性研究[21-22]。为封闭求解的湍流方程引入SST k-ω湍流模型，它可以准确捕捉管内的流动分离和激波[23]。根据以往的研究[12-15]，由于管内激波和膨胀波的存在，气体温度T发生了巨大变化，所以管内空气的动态黏度 µ服从Sutherland定律，即：

式中：参考动态黏度µ0=1.716×10-5Pa·s； 参考温度T0= 273.15 K；Sutherland常数S=111 K 。

本文采用了耦合流隐式求解器来求解方程。为了提高求解器产生的线性系统的稳健性和收敛速度，本文运用了代数多重网格（AMG）算法。选择AUSM+格式来处理对流通量，可以准确捕捉到激波的不连续性[13-14]。对流项采用二阶迎风/有界中心差分混合方法进行离散，混合方案表达如下：

图4 计算网格的布局展示Fig.4 Configuration of the computational grid

式中：m˙表 示通过面f的质量流率；ϕSOU和 ϕBCD分别是通过二阶迎风（SOU）插值和有界中心差分（BCD）插值得到的单元面值；σ为混合系数，本文设为0.15。

时间项和离散化分别通过二阶精度隐式格式和双时间步格式处理。在列车加速阶段，时间步长保持动态自适应，以确保满足库朗数小于1的要求。在列车匀速运行阶段，时间步长为1.2×10-4s。磁浮列车在管道内运行的物理时间为1.75 s。在128核的高性能计算机上，总计算时间约为480 h。

2 验证

2.1 网格独立性研究

为了开展网格敏感性分析，本文划分了三种具有相同网格策略、不同密度的网格。粗、中、细网格总数分别为1269万、2638万和4932万。表1列出了三组网格的关键网格参数。为了匹配IDDES模型对网格的要求，三套网格保持相同的近壁棱镜层厚度。此外，为了进一步研究边界层网格的独立性，与粗网格和中等网格相比，细网格包含更多的棱柱层。图5展示了中等网格计算时，列车上下表面中心线上的y+分布。列车上下表面的y+值大多小于1，最高不超过1.5，这符合IDDES模型对网格的要求。

表1比较了三组网格计算的气动阻力和相对误差。这里的相对误差是指粗网格和中网格计算的阻力值与细网格计算的相对差异。中等网格的预测结果与细网格的预测结果相似，阻力相对误差约1%。

表1 网格分辨率的比较Table 1 Comparison of the grid resolution

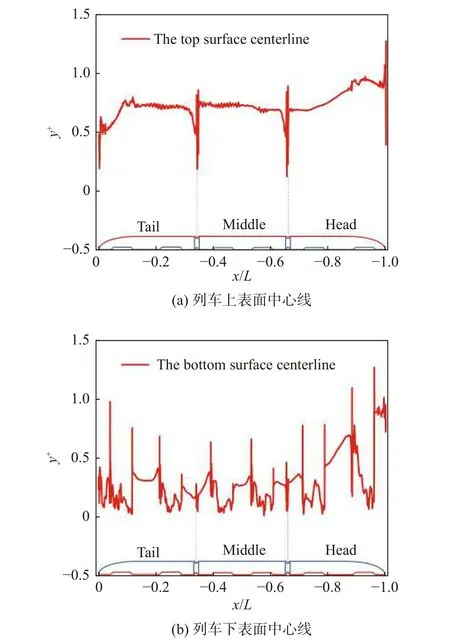
图5 列车表面y+分布Fig.5 y+ distribution along the train surface

图6比较了三套网格计算的尾流区域压力沿流动方向的波动情况。由结果可知，中网格和细网格计算的压力波动分布是相似的，而粗网格尽管可以捕捉由波系引起的压力波动趋势，但是与其他两套较细的网格相比，波动幅值有较大差异。

网格独立性研究表明，中等网格具有足够的分辨率。因此，在这项工作中，中等网格密度可用于研究真空管道磁浮交通管内波系时空分布特征。

图6 z = 1 m截面中心线上列车尾流压力分布比较Fig.6 Comparison of the pressure distribution in the wake region along the centerlineof a cross section at z = 1 m

2.2 与风洞实验数据比较

为了进一步验证本文采用的数值算法捕捉管内波系（激波和膨胀波）的能力，将数值模拟结果与Kayser和Whiton[24]在兰利研究中心的8英尺跨声速风洞测试所得的试验数据进行比较。风洞试验测试的马赫数（Ma= 1.2）与本研究中列车的马赫数非常接近。图7给出了风洞试验所用几何模型SOCBT及其尺寸，模型直径D为0.057 m，攻角为4°。

图7 SOCBT模型尺寸Fig.7 Size of the SOCBT model

如图8所示，数值模拟结果与实验数据吻合良好，本文采用的方法也能准确捕捉激波/膨胀波的位置。此外，模型迎风侧表面的压力系数Cp大于背风侧。压力系数Cp定义如下：

式中：p 和p0分别表示表面静压和参考压力，ρ为空气密度，V为入口速度。

通过网格独立性和风洞试验验证，可以得出本文采用的数值模拟方法和网格划分策略可用于真空管道交通管内波系分布和流场结构特征的研究。

3 结果与讨论

3.1 管内流场时变特性

本节主要分析管内流场时变（加速阶段和匀速阶段）分布的特性，分别对列车前方区域和尾流区域的流动特点进行描述。

图8 SOCBT压力系数分布Fig.8 Pressure coefficient distribution of the SOCBT model

1）列车前方流场时变特性。如图9所示，在加速阶段，列车加速向前运动会不断产生压缩波，压缩波以当地声速向前运动，后产生的压缩波速度比先产生的压缩波快，这样后产生的压缩波不断追上前方的压缩波，形成一道正激波[25]，这里把前方正激波定义为NSWL。

图10给出了不同时刻下y = 0截面的列车前方马赫数分布云图。在加速阶段，NSWL的强度随着列车速度的增加逐渐增强。这里激波的强度定义为波前后气流参数（马赫数）的变化。在匀速阶段，列车速度保持不变，没有新产生的压缩波，所以NSWL的强度保持不变，但是正激波NSWL和列车之间的距离随着运行时间线性增加（图11）。

图9 列车前方正激波形成示意图Fig.9 Schematic diagram of the normal shock wave formation in front of the train

图10 列车前方马赫数时变分布特征Fig.10 Time-varying Mach number distribution characteristics in front of the train

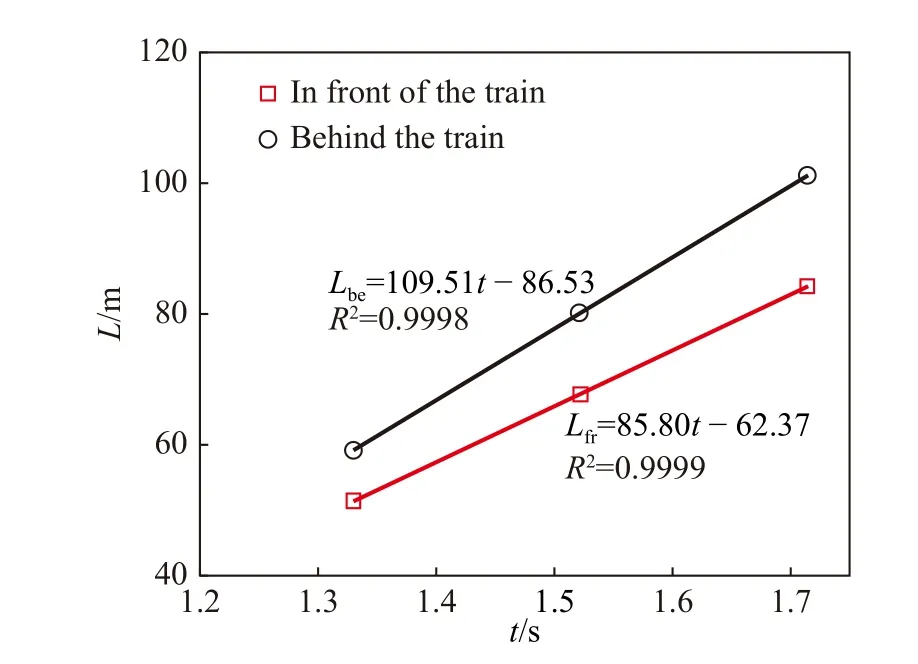
图11 匀速阶段时激波扰动区长度与列车运行时间的关系Fig.11 Relationship between the length of the disturbed region and the train movement time in the uniform speed operation phase

图12 尾流区域马赫数时变分布特征Fig.12 Time-varying Mach number distribution characteristicsin the wake region

2）尾流区域流场时变特性。图12给出了不同时刻下y =0截面的列车尾流区域马赫数分布云图。可以明显看出相比于列车前方区域，尾流区流动非常复杂。在t =0.672 s，尾车附近出现了局部超声速区域，形成了斜激波S1。在t=0.768 s，S1处于不稳定状态，相较于t =0.672 s，S1的位置更靠近尾车鼻尖。同时S1向管道壁面传播反射，形成反射激波。尾流区域也出现了正激波，这里称为NSWT。随着列车继续运动，激波S1的位置不断接近尾车鼻尖，且在管道壁面反射传播。

此外，尾流区域涡的分布也较为紊乱，随着列车速度增加，尾涡紊乱程度先增大后减小。在激波出现的地方，涡紊乱程度较小，激波占据主导地位。在匀速阶段，正激波NSWT和列车之间的距离随着运行时间线性增加（图11），这和文献[12]的结论一致。

3.2 管内流场空间分布特征

本节以t = 1.75 s时刻为例，分析管内流场的空间分布特征。

1）列车前方流场空间分布特性。图13为列车前方压力空间分布云图，列车前方正激波（NSWL）作为一个分界面将列车前方的流场分为激波扰动区和未扰动区，未扰动区的流场物理量与管内初始流场的物理量一致，而激波扰动区是一个正压区。

图13 列车前方压力空间分布Fig.13 Spatial distribution of pressure in front of the train

为进一步量化分析，图14比较了不同位置处的列车前方压力分布，其中Line 1（z =0 m）位于纵截面y =0 m，Line 2（y =0 m）位于水平截面z =2 m。对比发现，两条线探针上的压力分布几乎无差异，除了头车鼻尖附近因端部效应造成的影响。这里可以认为列车前方的激波扰动区域呈现准一维分布特性。

图14 列车前方不同位置处压力分布对比Fig.14 Comparison of pressure distributionsat different positionsin front of the train

2）尾流区流场空间分布特性。图15为尾流区域压力空间分布云图，列车尾流是一个负压区域，并且激波和膨胀波在管道壁面反射传播。

图16给出了中心纵截面y = 0 m处尾流拓扑结构示意图。在先前基于轴对称车/管模型的研究中，列车尾流区域的特点主要是有规律地交替出现一系列斜激波和膨胀波[5,7,12-14]。在本文中，由于考虑了悬浮间隙，尾流区域的波系分布呈现明显的上下不对称性。在尾车流线型区域，出现了经典的Prandtl Meyer等熵流，气流加速，压力下降。由于过度膨胀，尾车压力小于未受干扰的环境压力。在磁悬浮列车的上、下表面分别产生了两个斜激波（S1和S2），使得流动转向和压力上升。S1与管道上壁面相互作用，形成反射激波S3。同时，由于S1和S2引起的反向压力梯度，尾车鼻尖附近发生流动分离，形成剪切层[15]，增加了尾流区域流动的不稳定性。当剪切层重新附着在地面时，形成了一个再附着激波S4，之后剪切层逐渐远离地面。S3和S4发生了不规则相交。另外，当激波与不稳定的剪切层相互作用时，会产生局部分离泡。

图15 尾流区域压力空间分布Fig. 15 Spatial distribution of pressure in the wake region

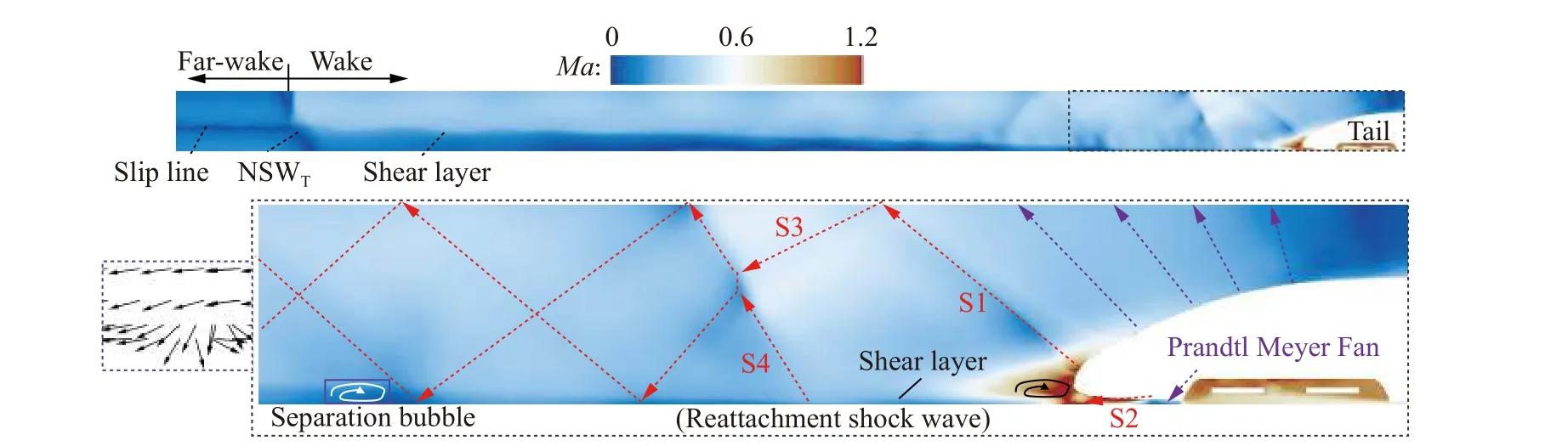
图16 y = 0 m截面上尾流拓扑结构示意图Fig.16 Schematic of the wake flow topology in the crosssection at y = 0 m

斜激波和膨胀波在管道壁面不断反射和传播。由于波系的能量被空气黏性耗散，波系的强度逐渐减弱。在斜激波和膨胀波停止传播的位置形成了尾部正激波（NSWT），用来恢复膨胀波造成的压力下降。与以往基于轴对称车/管模型的研究结果不同[5,7,12-14]，本研究中的NSWT与x轴有一个角度，这是由于剪切层造成z方向上物理量分布不均匀。此外，气流经过NSWT后，虽然在远尾迹区域的压力是均匀分布的，但由于剪切层的存在，上下区域的气流速度存在差异，因此在远尾迹区域可以看到一条与剪切层相连的滑移线。

图17对比了不同高度水平面上（z =0、1、2、3 m）尾流流场的结构分布。对比发现，不同高度水平面的流场结构差异较大。在近地面上（z =0、1 m），尾流较为紊乱，波系分布不明显。随着远离地面，紊乱程度降低，且能够明显观察到波系的传播与反射。为了探究这种差异，图18通过等值面Q = 5000来可视化尾涡结构。

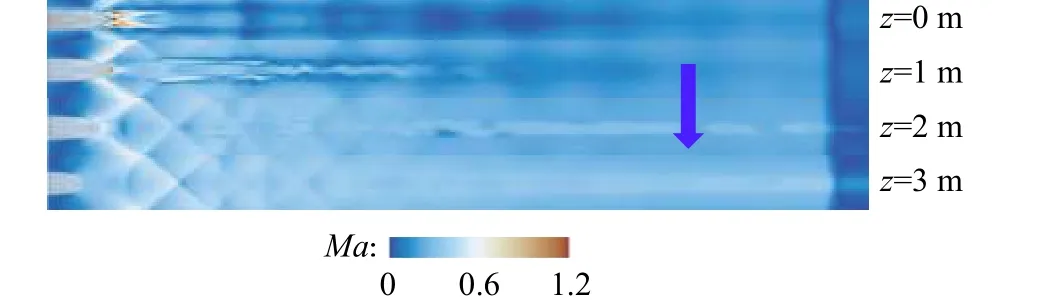
图17 不同水平截面上尾流流场结构Fig.17 Wake structuresat different horizontal crosssections

图18 尾流涡结构Fig.18 Vortex structures in the wake region

从图18可以看到尾流区域存在一对反向旋转的涡，并且涡对沿着轨道螺旋上升。在近地面上（z =0、1 m），正是因为涡对的影响使得尾流较为紊乱。激波与涡对的相互作用增加了尾流的复杂程度，也是空气动力学中常见的流动现象。在后续工作中还要继续深入研究管道中涡-激波的相互作用特性，本文不再对此展开。

为了进一步量化分析，图19比较了不同位置处的尾流区域压力分布，其中Line 3（z = 3.8 m）和Line 4（z =-0.5 m）均位于纵截面y =0 m处。对比发现，两条线探针上的压力分布差异较大，特别是尾车鼻尖附近。具体来说，首先是由于截面变化率不同，列车上表面和下表面产生的膨胀波扇的强度有较大差异，下表面的膨胀波扇长度较小，但是导致的压力变化梯度大。其次是由于鼻尖附近流动分离引起了较大的压力波动。

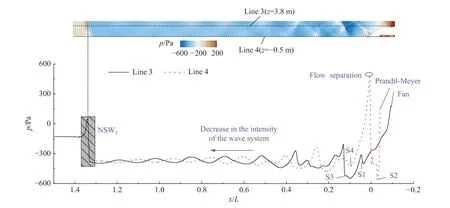
图19 尾流区域不同位置处压力分布对比Fig.19 Comparison of pressure distributions at different positions in thewake region

4 结论

本文基于IDDES湍流模型及重叠网格技术，研究了高温超导磁悬浮列车在启动加速阶段和匀速阶段的管内波系时变分布特征。根据仿真结果，得出以下结论：

1）列车加速向前运动会不断产生压缩波，这一系列压缩波形成一道正激波，正激波将列车前方的流场分为激波扰动区和未扰动区。未扰动区域的流场物理量与管内初始流场的物理量一致；而激波扰动区是一个正压区，在匀速运行阶段，呈现准一维分布特性。

2）列车尾流区较为复杂，存在着激波、膨胀波、涡对以及它们间的相互作用等复杂流动现象。在加速阶段，在t =0.768 s，列车上表面开始形成斜激波，随着列车进一步加速，一方面斜激波向列车运行反方向运动，另一方面会向管道壁面传播反射，形成反射激波。在匀速阶段，尾流正激波和列车之间的距离随着运行时间呈线性增加。

3）相较于轴对称车/管模型下的波系分布，考虑悬浮间隙时，尾流区域的波系分布呈现明显的上下不对称现象。特别是列车上下表面产生的膨胀波扇以及流动分离形成的剪切层。

4）尾流区域存在一对反向旋转的涡，并且涡对沿着轨道螺旋上升。在近地截面上，由于激波与涡对的相互作用使得尾流较为紊乱，波系分布不明显。随着远离地面，紊乱程度降低，且能够明显观察到波系的传播与反射。

5）本文研究的列车最高运行速度为1500 km/h，下一步研究中，将系统性地研究多个速度域（亚声速、跨声速和超声速）下管内波系分布特性，服务多态耦合轨道交通动模型试验平台的建设。

致谢：感谢中铁第四勘察设计院集团有限公司高温超导磁浮低真空管道工艺研究（2019K118）项目的资助。