面向爆轰冲击的分离式流固耦合数值模拟
2023-01-05郭晓威甘新标龚春叶杨文祥
张 森,郭晓威,*,甘新标,龚春叶,杨文祥,李 超
(1.国防科技大学计算机学院,量子信息研究所兼高性能计算国家重点实验室,长沙 410073;2.中国空气动力研究与发展中心,绵阳 621000)
0 引言
爆轰波的冲击响应通常涉及高温高压下的流体动力学,以及固体的变形和损伤等。这一复杂过程固有的多物理和多尺度特性导致了实验的高成本和高难度。随着高性能计算技术和数值模拟方法的发展,对爆轰冲击下固体响应进行数值模拟已成为一种有效的工程研究方法[1-3]。
爆轰传播是一个典型的两相或多相流问题。考虑到不同域(如炸药和空气)之间跨界面的跳跃条件,该问题的主要数值难点是精确计算界面运动,可能的解决方法包括界面跟踪法[4]、基于界面重构过程的VOF(volume of fluid)方法[5]、水平集(level set,LS)方法[6]、扩散界面法[7-9]等。其中扩散界面法不需要计算界面的精确位置,而需要为过渡层中的混合物引入与扩散界面相对应的混合物模型或人工状态方程。利用这一方法,Larrouturou提出了适用于理想气体状态方程的γ模型和质量分数模型[7]。然而,这些模型可能导致压力或速度在界面上的振荡。为了解决这个问题,Abgrall和Karni将γ模型的非保守方程应用于该问题[8]。Shyue通过添加更多与状态方程中所用参数相对应的输运方程,将该模型扩展到其他类型的状态方程[9]。此外,离散玻尔兹曼方法(DBM)应用在爆轰燃烧领域并取得进展[10],张玉东等基于离散玻尔兹曼模型,模拟和研究了四种不同反应速率的爆轰现象,从水动力量、非平衡量和熵产三方面研究了四种起爆方式的差异[11]。blastFoam[12-13]是Synthetik applicated Technologies基 于 开 源 软 件OpenFOAM开发的适用于高爆轰、爆炸安全、气流和一般可压缩流动的单相多相可压缩流动库,包括13个状态方程,允许在极端条件下对各材料进行建模。blastFoam提供了一个比较完善的功能来模拟爆轰波的传播过程,但是无法模拟爆轰冲击引起的固体变形和损伤。固体的损伤变形可通过固体力学进行建模计算,采用有限元方法对数学模型进行离散。开源有限元框架deal.II[14]是一个支持创建有限元代码的C++程序库,该程序库包含网格处理和细化、自由度处理、网格输入和图形格式的结果输出等细节。
流固耦合(fluid structureinteraction,FSI)的主要理论模型可以从流体动力学和固体力学的建模中得到。但是,除了单一的物理模型外,还需要考虑不同物理模型之间的相互作用。流固耦合数值模拟一般采用整体式或分离式方法。整体式方法将耦合系统作为整体来推导全局方程,然后用统一的方法对其进行离散求解。该方法是鲁棒且高效的,但其模块化不足,在解决新问题时无法重用已有的代码,需要进行重构、离散化、编码。分离式方法固有的灵活性,可以重用现有相对成熟的单物理场求解器,快速开发代码,并能在有限的时间内快速解决问题。
分离式方法将FSI问题分解为多个域,分别求解每个子域,并通过不同域之间的接口进行耦合。分离式FSI主要包括两个任务,即:流体与固体方程之间的耦合格式和流体与固体在界面上的数据映射。在过去的几十年中,拟牛顿耦合方法变得越来越重要。Michler等提出的interface-Newton-Krylov方法[15]是第一个拟牛顿耦合方法。之后,Vierendeels等在块迭代系统的基础上,提出了界面块拟牛顿最小二乘(IBQN-LS)耦合方案[16],Degroote等提出了界面拟牛顿逆最小二乘法(IQN-ILS)[17],Bogaers等提出了多矢量拟牛顿(MVQN)格式[18]。对于数据映射方法,常用的有最近邻法、最近投影法、径向基函数映射法等。精确代码交互耦合环境preCICE提供了多物理耦合所需的所有组件,包括通信方法、数据映射方法以及基于拟牛顿耦合方法的高效和健壮的耦合迭代技术[19-21]。
分离式方法具有良好的功能可扩展性和灵活性,但其收敛效率和并行可扩展性通常较差。De Nayer等采用基于CoMA的分离式方法模拟了带有柔性分流板(PfS-1a)的圆柱绕流[22],其效率和可扩展性受顺序耦合格式和集中式工具的限制,客户端与服务器之间的通信存在瓶颈。为解决上述问题,我们基于点对点的通信布局来传输耦合数据,消除瓶颈。
综上所述,本文针对爆轰冲击下的固体响应,基于开源软件OpenFOAM(blastFoam[12])、deal.Ⅱ[14]、preCICE[19]实现分离式流固耦合的求解系统,兼具灵活性和可扩展性,同时采用具体实例,即三维竖直墙体在高爆轰作用下的运动过程,进行数值模拟,并对模拟结果进行分析和讨论,以验证求解系统的正确性。
1 数值方法
分离式流固耦合数值求解部分包含三个模块,即流体计算模块、固体计算模块和耦合计算信息交换模块。各个模块的数值方法也不尽相同。
1.1 流体计算模块
爆轰波传播是一种高度可压缩的超音速流动。基于OpenFOAM软件框架和blastFoam库,采用有限体积法对流体模型进行离散求解。
作为流体动力学的基本控制方程,Navier-Stokes(N-S)方程主要由连续方程、动量方程和能量方程三个基本物理守恒定律组成。N-S方程可以表示为:

其中,U指由体积分数、质量、动量和能量组成的矢量,F 指相应的通量,S表示源项的向量。它们被定义为:
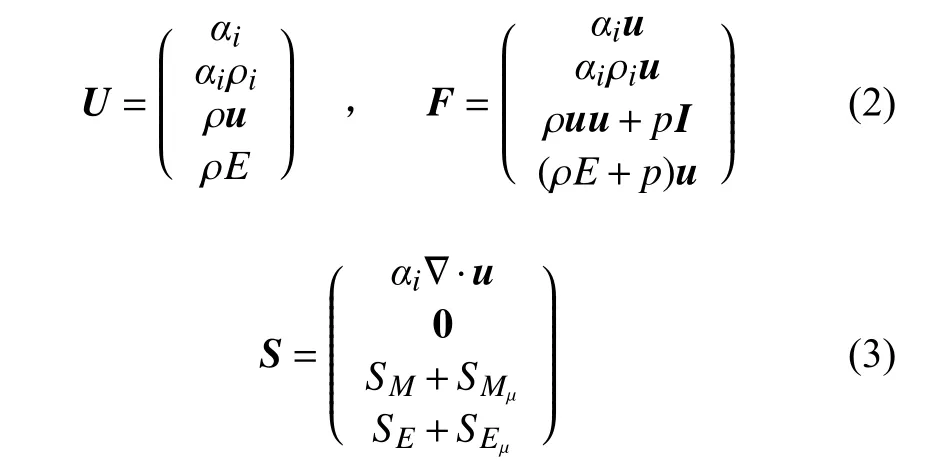
式中:u表 示混合物速度,I 表示单位矩阵,ρ指混合物密度,E 指总能量,p表示压力,SM和SE是指动量和能量源项, SMµ和SEµ指黏性项,αi和ρi表示每相的体积分数和密度。所有体积分数之和定义为1,混合物的密度ρ由各相的体积分数和密度确定,表示为ρ=
压力由一个特定的状态方程来定义,在这个状态方程中,混合物的内能、密度和体积分数被用来计算总压力。状态方程的Mie-Grüneisen形式使用理想气体项和偏差项来计算压力,即:

其中,Γi是Grüneisen系数,e是材料的内部能量,Πi指与理想气体的压力偏差。同时,声速表示为:

不同的材料对应不同的状态方程。对于理想气体,满足Γi=γi,Πi=0;对于硬化气体,满足Γi=γi,Πi=γiai,其中,γi表示比热比,ai表示参考压力。对于高能炸药,Jones Wilkins Lee(JWL)状态方程是最常用的描述高能炸药的状态方程,系数满足:
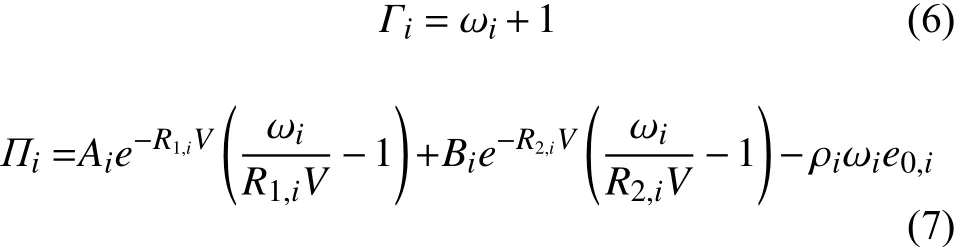
1.2 固体计算模块
假设固体为线性弹性的,则可用弹性方程描述固体的运动。在deal.II软件框架的基础上,采用有限元方法对固体计算模块进行离散求解。
控制方程主要由运动方程、本构方程和应变位移方程组成,即:
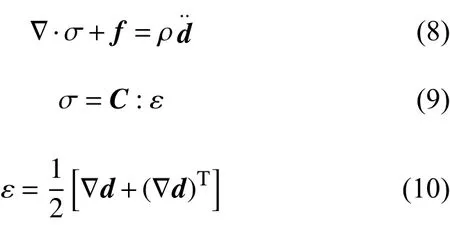
其中,σ表示Cauchy应力张量,f表示单位体积的体积力,ρ表示质量密度,d 表示位移矢量,表示d对时间的二阶导数。C表示四阶刚度张量,ε表示无穷小应变张量,运算符“:”表示两个张量的内积。
在各向同性介质中,本构方程可简化为:
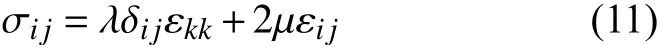
其中,λ表示Lamé第一参数,µ表示剪切模量,两者都是Lamé参数。
在通过接口数据通信获得应力后,可将应力代入本构方程(9)求解应变,然后代入应变位移方程(10)求解位移。最后,将经过一个时间步长后的位移通过接口数据通信发送给流体计算模块,完成耦合交互。
1.3 耦合计算信息交换模块
对于分离式FSI,假设两个求解器F 以及S,分别等价于映射和S。一个求解器将耦合接口上的输入向量映射到输出向量,并将其发送到另一个求解器。也就是说,以固体边界上的位移D( 或速度V)作为流体求解器的输入,计算作用到固体上的应力F作为输出;固体求解器将这些应力作为输入,并计算位移(或速度)作为输出。数学形式表示为:

分离式流固耦合数值模拟中的时间步可以在流体或固体求解器中通过少量固定数量的时间步来完成,也可以通过迭代过程直到收敛。前者对应于显式耦合格式,后者对应于隐式耦合格式,两者都有串行和并行格式。
串行显式格式首先使用旧时间步的位移值dn作为输入来运行流体求解器,并获得下一时间步的输出应力值 fn+1。然后使用输出应力值 fn+1作为输入来运行固体求解器以获得下一时间步的位移值dn+1,即:
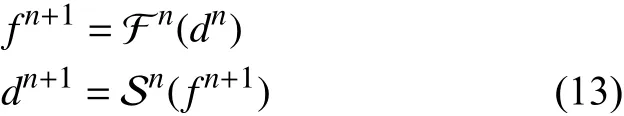
在串行显式格式中,两个求解器是交错运行的,因此在负载平衡和最大化并行性方面不是最优的。并行显式格式使用旧时间步的位移和应力值(dn,fn)作为两个求解器的输入,以获得下一时间步的位移和应力值(dn+1,fn+1):

两个解算器之间没有依赖关系,因此可以在同一时间步中同时执行。然而,这两种方案都可能导致不稳定,可以使用迭代方法迭代执行两个求解器,直到收敛。对于串行隐式格式,表达式为:
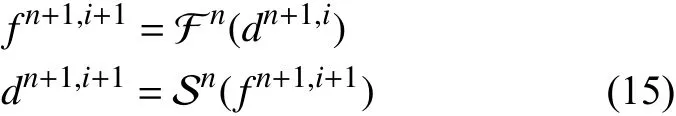
而对于并行隐式格式,表达式为:
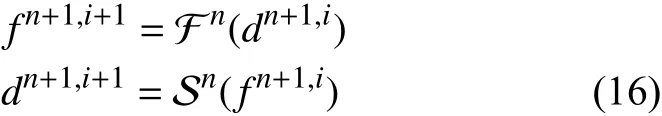
当迭代收敛时,则满足:
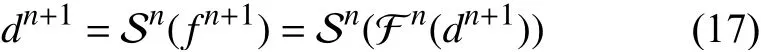
由于求解器之间相互独立,所使用的网格在界面上可能会出现不一致的情况,因此需要在不匹配的网格之间进行数据映射。常见的数据映射方法有最近邻映射、最近投影映射、径向基函数(RBF)映射等。
求解器之间通信的主要任务是交换耦合数据。开源耦合库preCICE为通信任务提供了解决方案,使用MPI或TCP/IP套接字建立通信。在耦合模拟之前,preCICE将在每个求解器进程之间建立一个通信通道,每个并行求解器将选择一个进程作为“主进程”来控制整个数值模拟过程。在通信过程中,采用了点对点的通信方式,不使用任何中央服务器。通过先前建立的通信通道,各求解器进程之间的通信是本地和异步的[19]。
2 验证算例的几何构型与参数配置
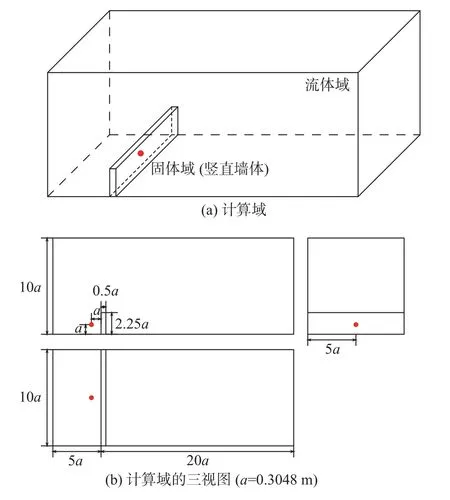
图1 测试算例的计算域示意图及其三视图Fig.1 Computational domain and itsthree views
采用三维竖直墙体在高爆轰作用下的运动过程作为测试算例验证和分析流固耦合数值模拟的求解系统。测试算例的计算域示意图及其三视图如图1所示,计算域分为两部分:流体部分和固体部分。固体部分为0.5a ×2.25a ×10a的竖直墙体,流体部分则是立方体空间内去除竖直墙体剩下的区域。红点表示爆轰中心,距固体和下边界的距离均为0.3048 m。在中心截面处竖直墙体周围设置了六个采样点,采样点的分布情况如图2所示,红点表示爆轰中心,青点表示各采样点。使用两种不同规模的网格(分别为457.6万和764万个单元)进行网格无关性检验,结果如图3所示。由图中可以看出采样点1和2处的压力变化与网格规模无关,因此数值模拟的结果与网格规模无关。下文中除并行测试外的数值模拟结果均采用以下结构化网格,即流体网格包含466.9万个点,1382万个面和457.6万个单元。爆轰中心附近和流体与固体界面处的网格较密集,远离爆轰中心处网格较稀疏。固体网格包含64.8万个点、59万个面和19.2万个单元,自由度为618723。
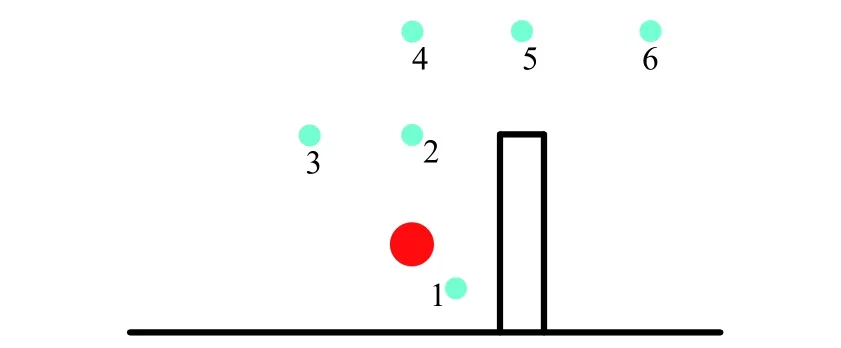
图2 中心截面处竖直墙体周围的采样点分布示意图Fig. 2 Distribution of sampling pointsaround the central section of the vertical wall
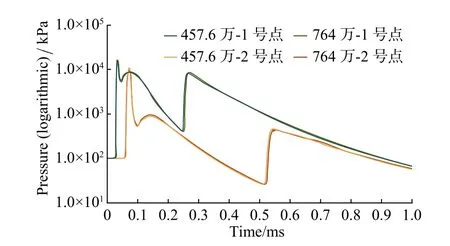
图3 网格无关性检验(采样点1和2处的压力变化)Fig.3 Mesh independency test(pressure at sampling points1 and 2)
流体部分由两相材料组成,即C4炸药和空气。各相材料的状态方程类型及其系数值如表1所示。C4炸药的状态方程类型为JWL,而空气的状态方程类型为硬化气体(Stiffened Gas)。对于固体部分,竖直墙体的材料由三个参数决定,即密度(ρ)和两个Lamé参数(λ 、µ)。混凝土墙体的密度为2440 kg/m3, λ为9.03×109,µ为13.54×109;铁板墙体密度为7000 kg/m3,λ为102.42×109,µ为80.47×109。
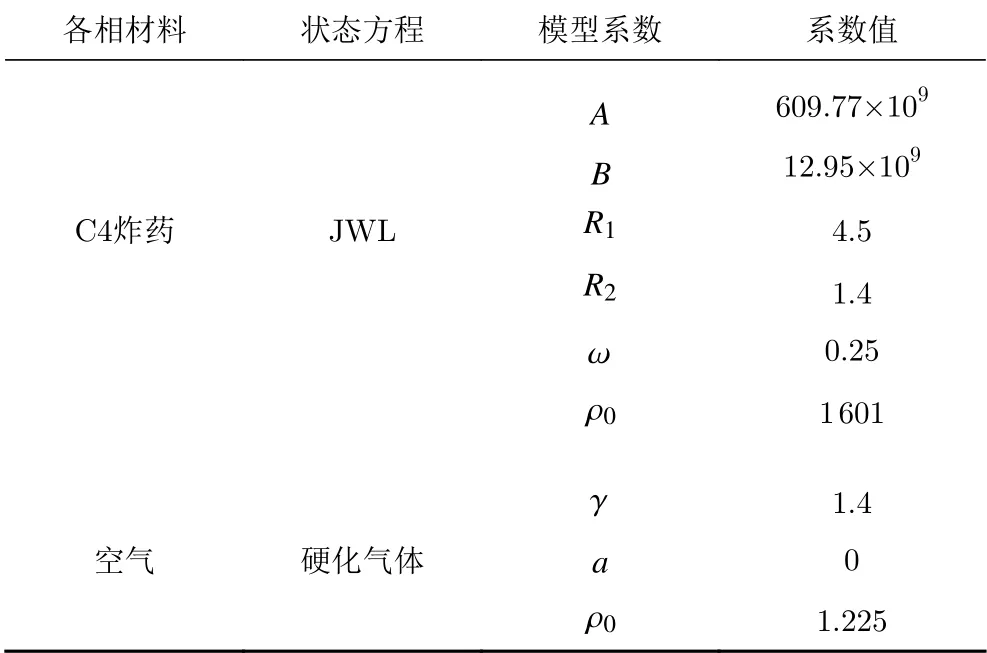
表1 流体计算模块各相材料的状态方程及其系数值Table1 The EOSand coefficients of each phase in the fluid module
数值格式是数值模拟的重要部分。对于流体求解器,通量格式选择HLLC格式;一阶时间导数项格式选择二阶强稳定Runge-Kutta(RK2SSP)格式;从单元中心到面中心的插值格式为cubic插值,标量的重构格式是vanAlbada,向量的重构格式是vanAlbadaV。除此之外,梯度格式为faceMDLimited leastSquares 1.0、表面法向梯度格式为corrected、拉普拉斯格式为Gauss linear corrected。对于固体求解器,选择具有二阶精度的Crank-Nicolson格式。
对于耦合计算信息交换模块,耦合交互的数据为位移和应力,数据映射方法采用最近邻映射。耦合格式采用串行隐式格式(方程(15)),加速格式采用IQN-ILS[17]方法。
3 结果与讨论
算例是在高性能计算平台上进行测试的,该平台包含数百个计算节点,每个节点包含两个Xeon E5-2620处理器(6核,2.10 GHz)。
图4是Beyer报告中的爆轰过程定性分析图,显示出高能炸药爆炸后的爆轰波传播过程。在高爆轰作用下,竖直墙体受到较大的冲击力,导致壁面变形。图5是三维竖直墙体在高爆轰作用下的运动过程的整体模拟图。该图包括竖直墙体的位移、流场中的速度流线和密度等值线以及下边界的速度分布。图中竖直墙体的材质为铁板,铁板墙体的变形程度小于混凝土墙体。

图4 Beyer报告[23]中的爆轰过程定性分析图Fig.4 A sketch of denotation process provided by Ref.[23]
炸药在爆炸点起爆后很快就扩散到竖直墙体。在0.04 ms左右,爆轰波首先与竖直墙面接触,但竖直墙面暂时没有受到冲击力的影响,尚未发生变形。在0.07 ms左右,竖直墙体所受到的压力高达10.20 GPa,此时竖直墙体在爆轰接触点处有轻微变形。从图5可以看出,随着时间的推移,竖直墙受到持续的应力,变形继续从初始接触点向外延伸。当爆轰波传播到竖直墙体下边界的角落处时,压力和密度不断积累。在0.2 ms时,墙角处的压力为最大压力,达到52.24 MPa,密度达到47.71 kg/m3。在0.6 ms时,竖直墙体的变形达到最大值,x方向偏移达到0.045 m。当爆轰波撞击竖直墙体及其下边界时,爆轰波反弹并向后传播。爆轰波向外传播,对竖直墙体施加力的作用,引起竖直墙体的变形。同时,由于竖直墙体的变形,爆轰波传播的计算域发生变化,从而影响爆轰波的传播。它们相互耦合、相互作用。爆轰波向外传播,与竖墙相互耦合,竖直墙体右上角出现漩涡。数值模拟结果展示的爆轰过程与Beyer[23]报告的爆轰传播过程相一致。
图6显示了竖直墙体在高爆轰作用下的形变过程。竖直墙体的材料为混凝土。在初始爆轰接触点处,首先形成凹面,然后变形向外扩展。当时间为0.71 ms时,垂直墙的位移达到最大值,x方向的最大偏移达到0.157 m。随着时间的推移,虽然墙体中间位置的x方向偏移逐渐减小,但墙体的变形范围仍在不断扩大。
图7、图8和图9分别显示了0.4、0.8、1.2、1.6 ms的速度流线图、压力等值线图和密度等值线图。此时,爆轰波经过下边界和竖直墙体的反弹后继续向外传播。0.3 ms后,竖直墙体右上方逐渐形成涡旋,流线规则地向外辐射,压力和密度在波面处发生跃变(包括初始波和反弹波)。当爆轰波向外传播时,涡逐渐变大并逐步发展为梭形涡。图7显示了中心截面后半部分的速度流线图,可以看出,在0.4 ms时,整个速度流线向外辐射,在竖直墙体的右上角开始出现一个小涡旋。
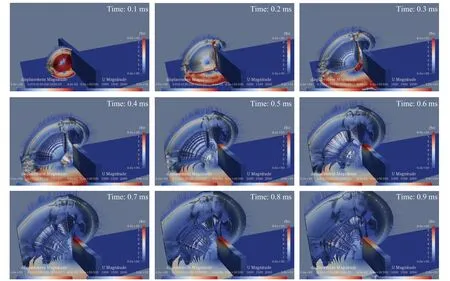
图5 三维竖直铁板墙体在高爆轰作用下运动过程的整体模拟图(时间跨度0.1~0.9 ms,间隔0.1 ms)Fig.5 The movement of a 3D vertical iron wall under the condition of a high-explosive detonation(the time span is0.1~ 0.9 ms,the interval time is0.1 ms)
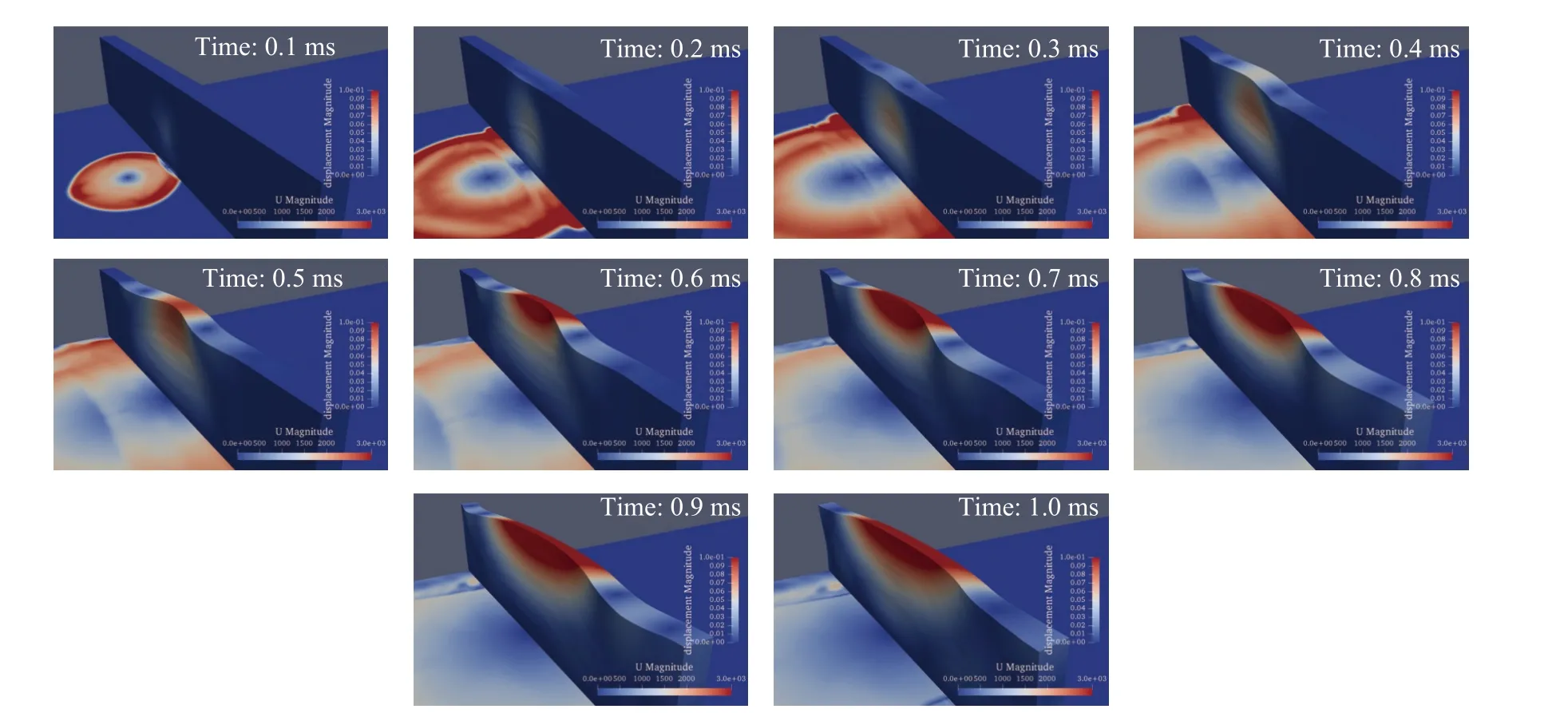
图6 三维竖直混凝土墙体在高爆轰作用下的形变过程图(时间跨度0.1~1.0 ms,间隔0.1 ms)Fig.6 The movement of a 3D vertical concretewall under the condition of a high-explosive detonation(the time span is0.1~ 1.0 ms,the interval time is0.1 ms)
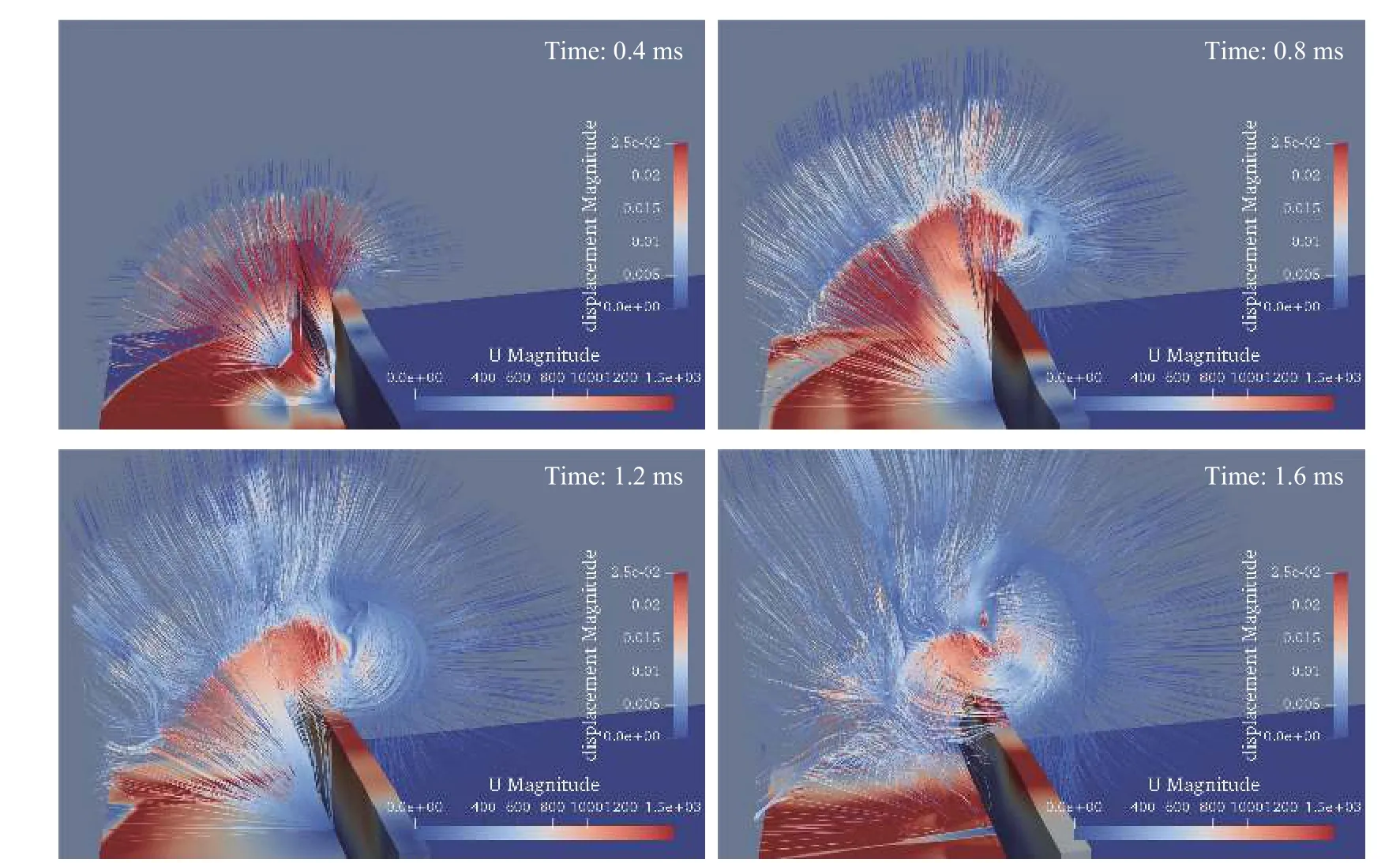
图7 中截面后半部分在0.4、0.8 、1.2、1.6 ms的速度流线图Fig.7 The velocity streamlinesin the second part of the central cross section at 0.4, 0.8 ,1.2,and 1.6 ms
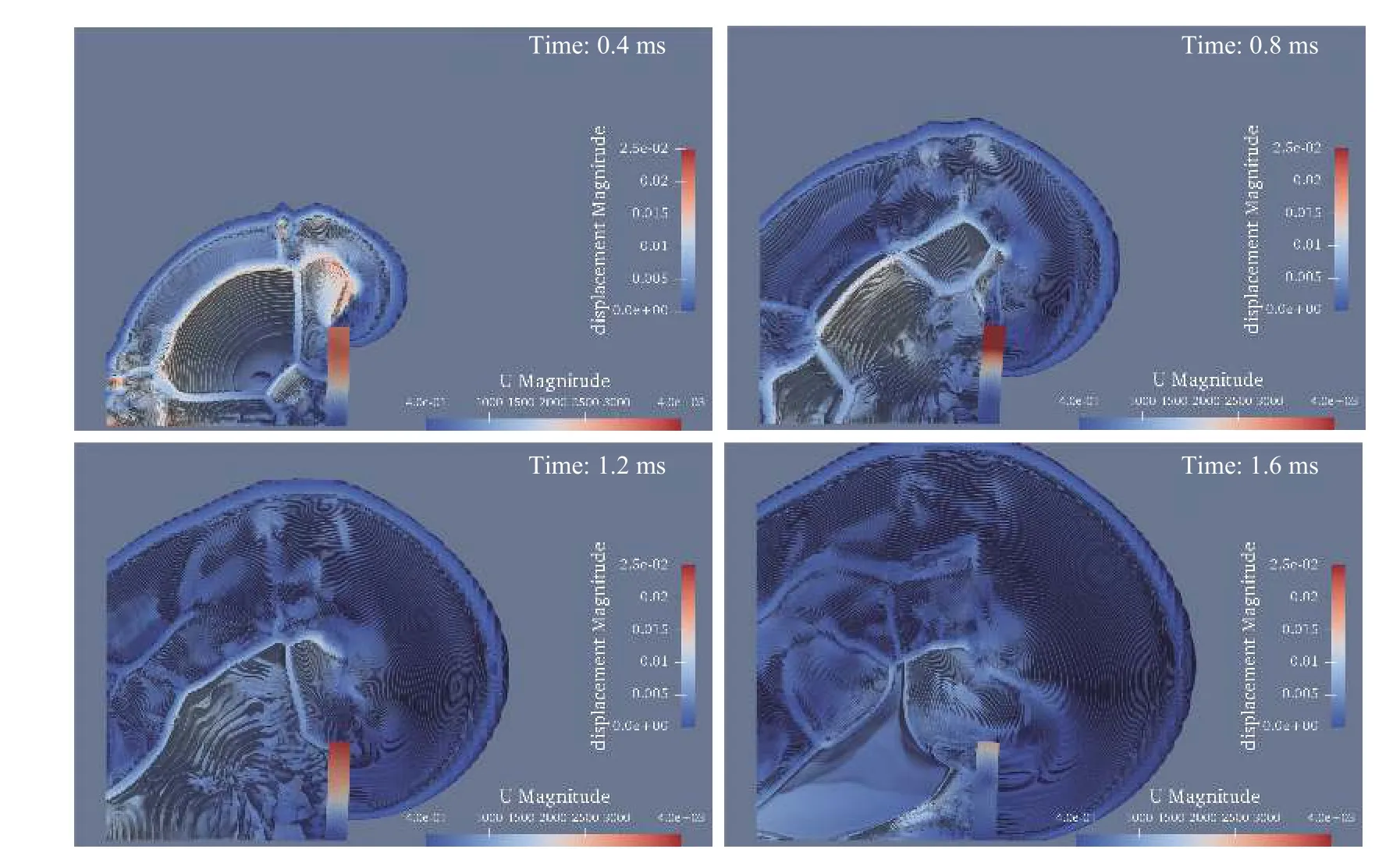
图8 中截面后半部分在0.4、0.8 、1.2、1.6 ms的压力等值线图Fig.8 The pressure contours in the second part of the central crosssection at 0.4, 0.8, 1.2, and 1.6 ms
在0.8 ms时,爆轰波向外传播,速度流线仍呈现向外辐射状。此时涡旋已经非常明显,同时呈现出梭形。在1.2 ms时,涡旋持续变大,流线出现混乱,不是规则的向外辐射状。在1.6 ms时,流线的混乱程度变大。图8和图9显示了中心横截面后半部分的压力等值线和密度等值线。可以看出,波面处的压力和密度发生跃变,波面处的压力和密度较高,而爆轰中心附近出现低压和低密度区。
各采样点处的压力-时间和密度-时间历程曲线如图10和图11所示。压力和密度在爆轰波传播到达的时候瞬间跳跃式增长,爆轰波传播过后则迅速下降。通过压力和密度变化的延迟情况可以判断出爆轰波到达的顺序。压力和密度出现了多次增长,表示初始波和反弹波经过了采样点。从图中可以看出,爆轰波最先到达1号采样点,压力最高达1.61296×107Pa,密度最高达到25.9997 kg/m3。随后到达2号、3号采样点。其他采样点处的密度最高到达5 kg/m3附近,之后不断下降趋近于零。

图9 中截面后半部分在0.4、0.8 、1.2、1.6 ms的密度等值线图Fig.9 The density contoursin the second part of the central cross section at 0.4, 0.8 ,1.2,and 1.6 ms
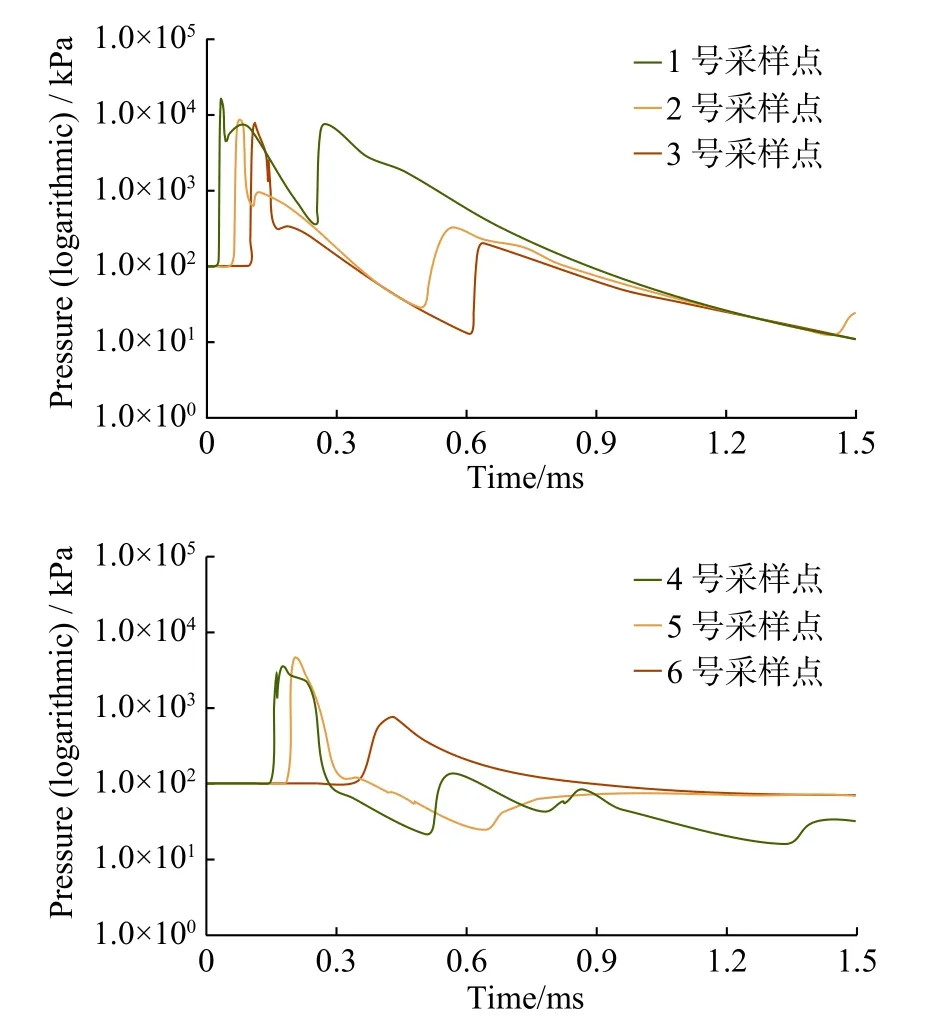
图10 采样点处的压力-时间历程曲线Fig.10 The time historiesof pressure
因为基于点对点通信模式和并行耦合格式,所以求解系统具有良好的并行可扩展性。我们设置了两种不同规模的网格(网格1:流体300万单元,固体10万单元;网格2:流体500万单元,固体10万单元),分别采用串行显式(方程(13))和并行显式(方程(14))耦合格式展开测试。图12显示了网格1和网格2在串行显式和并行显式耦合格式下的时间开销(400个时间步)和对应的加速比。对于同一网格,并行耦合格式的时间开销相比于串行格式减少大约36%(网格1)和28%(网格2)。在256核四个测试的加速比达到最大,分别为122.3(网格1-串行耦合),141.2(网格1-并行耦合),147.0(网格2-串行耦合),178.0(网格1-并行耦合)。
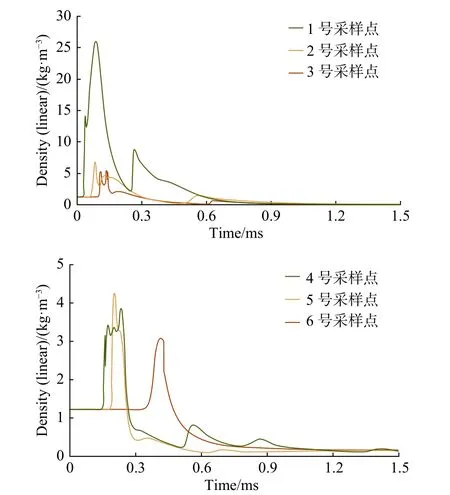
图11 采样点处的密度-时间历程曲线Fig.11 The time historiesof density
数值模拟给出了高能炸药在三维竖直墙体后起爆并传播的过程中各物理量的分布情况和高爆轰作用下竖直墙体的变形运动情况。模拟结果符合预期及爆轰过程的直观印象,可为相关工程应用的数字化设计和评价提供技术支持。

图12 网格1和网格2在串行显式和并行显式耦合格式下的时间开销(400个时间步)和对应的加速比Fig. 12 Thetime costs (400 time-steps) and the speedup ratios of Mesh1 and Mesh2 with serial-explicit and parallel-explicit coupling schemes
4 结论
爆轰冲击作用下固体响应过程的研究在诸多工程应用中,如损伤评估、建筑爆破、矿物开采等,具有重要意义。然而,在复杂的工程应用中,准确高效地模拟爆轰冲击作用下固体响应的过程存在许多困难和挑战。
本文采用分离式流固耦合的方法,基于开源软件OpenFOAM(blastFOAM)、preCICE和deal.Ⅱ实现数值模拟的求解系统,并利用三维竖直墙壁在高爆轰作用下的运动算例开展数值模拟。对于数值模拟结果,我们从爆轰响应整体过程、竖直墙体的形变过程、速度流线、压力和密度等值线、采样点处的压力和密度变化等方面详细展开分析。结果表明,该求解系统能够准确有效地模拟爆轰波传播的各个阶段以及高爆轰作用下竖直墙体的变形运动情况,模拟结果展示的爆轰过程与Beyer报告中的爆轰波传播过程一致。求解系统具有良好的并行可扩展性,在并行度为256核时的加速比达到141.2和178.0,并行效率分别达到55.2%和69.5%。总而言之,本文通过集成开放源代码,实现了面向爆轰冲击的分离式流固耦合数值模拟求解系统,该系统在诸多领域的工程应用中都具有重要的现实意义。
