基于磁偶极子的2阶磁场梯度张量缩并方法
2023-01-05江胜华
江胜华
(西南大学 工程技术学院,重庆 400715)
0 引言
磁性目标的磁场梯度张量定位技术,作为一种被动的定位技术,具有更丰富更深入的特征信息,包括梯度、张量不变量、特征值和模量等,其最大的优点是可以很大程度上克服地球磁场等背景磁场的影响,且不易受测量系统中朝向误差的影响,可以提高对磁性目标的定位精度[1-5]。其中,磁场梯度张量的不变量、模量和特征值等,与坐标轴方向无关,非常适合磁性目标的实时定位[6-8],已逐渐应用在水下/地下爆炸物探测、水下磁性物体探测、入侵物体探测、室内定位、体内微型诊疗装置定位[9-10]等多个领域。另一方面,铁磁金属试件可视为无数个微小的磁偶极子的组合,微小的磁偶极子与磁场传感器之间的关系可近似借鉴磁场定位的相关理论,磁场梯度张量可应用在金属缺陷、锈蚀、应力等损伤检测技术[11-12]。将磁场梯度张量的不变量、模量和特征值等进一步处理后,可得到更加丰富、细致和深入的定位特征信息。随着全张量磁力梯度仪的研制成功,为了适应不同的定位情景,也出现了各种不同构造和组合的全张量磁力梯度仪[13-14]。相应地,诸多学者发展了1阶磁场梯度张量的测量原理和算法,且已经应用在不同的领域。目前2阶磁场梯度张量亦开始逐渐应用在磁性物体的定位。Schmidt等[15]认为2阶磁场梯度张量比1阶磁场梯度张量在磁测反演时具有更高的分辨率。Clark[16]结合2阶和1阶磁场梯度张量计算了磁场梯度张量的特征值和不变量的导数,并应用在管道定位和矿床的几何形态及钻孔交点的定位,磁场反演结果与实际情况一致。Sui等[17]采用安装在一个旋转圆盘上的磁传感器进行了2阶磁场梯度张量的测量,认为2阶磁场梯度张量和1阶磁场梯度张量相结合使用,在一定程度上可降低定位时非唯一解和非真实解导致求解的模糊性。Li等[18]提出一种2阶磁场梯度测量系统,并采用2阶磁场梯度张量和欧拉方程进行磁场定位,结果表明2阶磁场梯度张量具有更强的消除背景磁场和抗干扰的能力。张涛等[19]通过十字型阵列、六面体阵列及9个传感器形成的菱形阵列3种全张量磁传感系统,在2 m×2 m的正方形区域内进行数值模拟,比较了1阶和2阶磁场梯度张量,结果显示:在消除地磁场方面,2阶磁场梯度张量更优;在消除干扰噪声方面,1阶磁场梯度张量略优。由于全张量磁力梯度仪的研制成功及发展,研究2阶磁场梯度张量,并与1阶磁场梯度张量结合使用,在磁场定位中将具有重要的研究意义和应用价值。
鉴于1阶和2阶磁场梯度张量测量设备的逐渐发展,同时2阶磁场梯度张量在磁测反演拥有更高的分辨率,处理特征值和不变量时具有更丰富、更细致的信息,更强的消除背景磁场和抗干扰的能力,可降低定位时非唯一解和非真实解导致求解的模糊性等多方面的优点,针对2阶磁场梯度张量的理论尚不够完善的现状,本文提出基于磁偶极子的2阶磁场梯度张量缩并方法,包括全局缩并和局部缩并的方法,提出2阶磁场梯度张量的全局模量和局部模量的计算公式,进行仿真分析,研究全局模量和局部模量及相关参数的三维空间分布规律,给出相关参数的近似计算公式,并比较2阶和1阶磁场梯度张量及模量随距离的规律。
1 基于磁偶极子的2阶磁场梯度张量
如磁性物体简化为磁偶极子,在测试系统处激发的磁感应强度矢量[20]为
(1)
式中:μ0为介质磁导率;m为磁性目标的磁矩m=(mx,my,mz),其中mx、my和mz分别为磁矩m沿着x轴、y轴和z轴3个方向的分量;r为磁偶极子至测量系统的位置矢量,r为r的模,r=|r|,即磁偶极子至测量系统的距离。磁感应强度矢量B可以用笛卡尔分量表示,即沿x轴、y轴和z轴3个方向的磁感应强度Bx、By和Bz。
磁偶极子的1阶磁场梯度张量[4,17]为
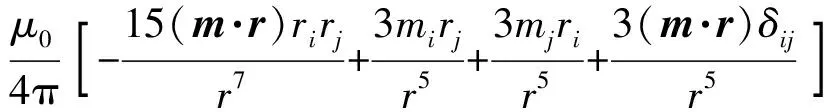
(2)
(3)
式中:i,j=x,y,z。
1阶磁场梯度张量G中共有9个参数,即Bxx、Bxy、Bxz、Byx、Byy、Byz、Bzx、Bzy和Bzz,分别为磁感应强度Bx、By和Bz沿x轴、y轴和z轴3个方向的梯度。9个参数中仅有5个独立的参数,即Bxx、Bxy、Bxz、Byy和Byz。
磁偶极子的1阶磁场梯度张量的全局模量CG为
(4)
式中:Gij表示矩阵Gij中的参数。
1阶磁场梯度张量的全局模量与磁偶极子的磁矩的模、磁偶极子至测量系统的距离等之间的关系[21-22]为
(5)

磁偶极子的2阶磁场梯度张量[17]为

(6)
δ=(δil,δjl,δkl)
(7)
式中:k,l=x,y,z。
磁偶极子的2阶磁场梯度张量展开成3个矩阵Hx、Hy和Hz:
(8)
式中:主对角元素满足:
Hxxx+Hyyx+Hzzx=0
(9)
Hx矩阵中共9个参数,但仅有5个独立的参数,即Hxxx、Hxyx、Hxzx、Hyyx和Hyzx。
(10)
式中:主对角元素满足:
Hxxy+Hyyy+Hzzy=0
(11)
Hy矩阵中共9个参数,但仅有5个独立的参数,即Hxxy、Hxyy、Hxzy、Hyyy和Hyzy。
(12)
式中:主对角元素满足:
Hzzz=-Hxxz-Hyyz
(13)
Hz矩阵中共9个参数,但仅有5个独立的参数,即Hxxz、Hxyz、Hxzz、Hyyz和Hyzz。
2阶磁场梯度张量H中共27个参数,由于(9)式、(11)式和(13)式,且考虑对称性,仅有7个独立的参数,即Hxxx、Hyyy、Hxxy、Hxxz、Hyyx、Hyyz和Hxyz。
2 基于磁偶极子的2阶磁场梯度张量缩并
定义磁偶极子的2阶磁场梯度张量的全局模量为
(14)
(14)式即为2阶磁场梯度张量全局缩并,将2阶磁场梯度张量H的全部27个元素变为一个标量CH。
定义磁偶极子的2阶磁场梯度张量局部模量CHx、CHy、CHz、CHxy、CHxz及CHyz,具体公式如下:
(15)
(16)
(17)
(18)
(19)
(20)
(15)式至(20)式为2阶磁场梯度张量局部缩并,将2阶磁场梯度张量H的若干元素变为标量CHx、CHy、CHz、CHxy、CHxz及CHyz。
根据(6)式可知,2阶磁场梯度张量的27个参数均与磁矩的模M呈正比,与距离的5次方r5呈反比,即H∝M/r5。根据(14)式,进一步得到全局模量CH亦与磁矩的模M呈正比,与距离的5次方r5呈反比,即CH∝M/r5。结合1阶磁场梯度张量的全局模量与磁偶极子的磁矩的模、磁偶极子至测量系统的距离等之间的关系[21-22],给出2阶磁场梯度张量的全局模量与磁偶极子的磁矩的模、磁偶极子至测量系统的距离等之间的关系为
(21)
式中:kH为仅与磁偶极子的轴线及磁性目标至测量系统连线夹角相关的参数。
由于H∝M/r5,通过(15)式~(20)式进一步得到局部模量亦与磁矩的模M呈正比,与距离的5次方r5呈反比,即CHx∝M/r5、CHy∝M/r5、CHz∝M/r5、CHxy∝M/r5、CHxz∝M/r5及CHyz∝M/r5。结合1阶磁场梯度张量的局部模量与磁偶极子磁矩的模、磁偶极子至测量系统的距离等之间的关系[21-22],给出2阶磁场梯度张量的局部模量CHx、CHy、CHz、CHxy、CHxz及CHyz与磁偶极子的磁矩的模、磁偶极子至测量系统的距离等之间的关系为
(22)
(23)
(24)
(25)
(26)
(27)
式中:kHx、kHy、kHz、kHxy、kHxz及kHyz为与磁偶极子的轴线和磁性目标至测量系统连线的夹角及r/r二者相关的参数。
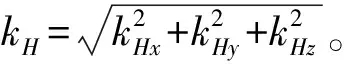
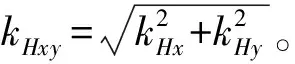
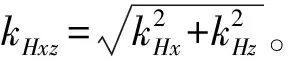

3 基于磁偶极子的2阶磁场梯度张量缩并的仿真分析
由(2)式和(6)式,可分别计算1阶和2阶磁场梯度张量,以Bxx、Byy、Bxy和Hxxx、Hyyy、Hxyz为例比较1阶磁场梯度张量和2阶磁场梯度张量,计算结果如图1~图2所示。在图1和图2中,计算Bxx、Byy、Bxy和Hxxx、Hyyy、Hxyz时,为比较二者的三维空间分布规律,取M=1.0 A·m2,r=|r|=1.0 m。由于1阶和2阶磁场梯度张量均与磁矩的模M呈正比的线性关系,当磁矩的模取其他值时,对关于1阶和2阶磁场梯度张量比较得出的结论没有影响;对于后续1阶和2阶磁场梯度张量的全局模量及相关参数的空间分布、相关参数具体取值的公式,以及1阶和2阶磁场梯度张量的全局模量与距离的关系比较得出来的结论,同样适用于磁矩的模取其他值的情况。

图1 1阶磁场梯度的三维空间分布Fig.1 3D spatial distribution of first-order magnetic gradient
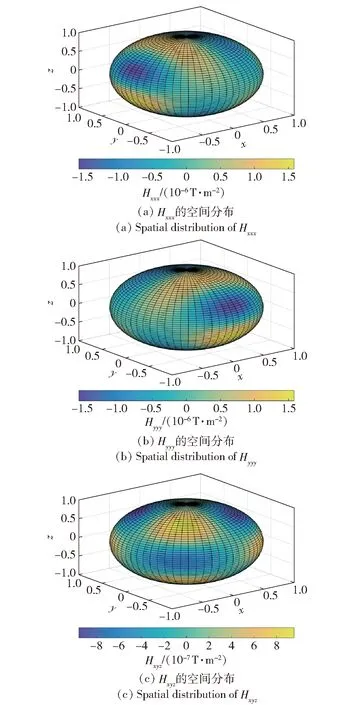
图2 2阶磁场梯度的三维空间分布Fig.2 3D spatial distribution of second-order magnetic gradient
由图1和图2可得,1阶磁场梯度Bxx、Byy和Bxy的范围分别为±4.13×10-7T/m、±4.13×10-7T/m和±2.88×10-7T/m;2阶磁场梯度Hxxx、Hyyy和Hxyz的范围分别为±1.58×10-6T/m2、±1.58×10-6T/m2和±9.64×10-7T/m2。在M=1.0 A·m2、r=|r|=1.0 m的情况下,Hxxx、Hyyy和Hxyz的绝对值最大值为Bxx、Byy和Bxy的绝对值最大值的3.35~3.83倍。
由(4)式和(14)式分别计算1阶和2阶磁场梯度张量的全局模量,即CG和CH,如图3~图4所示。在计算CG和CH时,取M=1.0 A·m2,r=|r|=1.0 m。

图3 1阶磁场梯度张量的全局模量CG的 三维空间分布Fig.3 3D spatial distribution of first-order magnetic gradient’s modulus CG
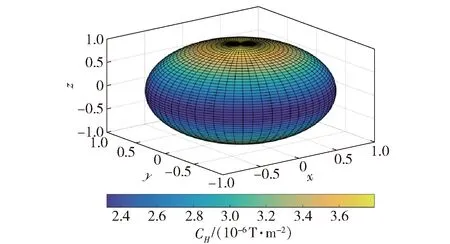
图4 2阶磁场梯度张量的全局模量CH的三维空间分布Fig.4 3D spatial distribution of second-order magnetic gradient’s modulus CH
由图3和图4可知,2阶磁场梯度张量的全局模量CH与1阶磁场梯度张量的全局模量CG极值分布相同:当ϑ=0°时(cos ϑ=m·r/(Mr),表示磁偶极子的轴线与磁性目标至测量系统连线夹角),CH与CG取最大值;当ϑ=90°时,CH与CG取最小值。
1阶磁场梯度张量的全局模量CG的范围为4.242 6×10-7~7.348 5×10-7T/m;2阶磁场梯度张量的全局模量CH的范围为23.238×10-7~37.947×10-7T/m2。在M=1.0 A·m2,r=|r|=1.0 m的情况下,CH最大值为CG最大值的5.16~5.48倍,其倍数大于磁场梯度张量(3.35~3.83倍)。
由(6)式、(14)式和(21)式,可计算kH值,其三维空间分布规律如图5所示,部分数值见表1。在计算kH时,取M=1.0 A·m2,r=|r|=1.0 m。

图5 kH值的三维空间分布Fig.5 3D spatial distribution of parameter kH

表1 kH值的理论反演值
由图4和图5可知,kH的三维空间分布规律与全局模量CH相同。同时,由表1可知,kH与距离r无关,只与ϑ有关。ϑ=0°时kH取最大值37.947 3;ϑ=90°时kH取最小值为23.237 9。
将kH值与角度ϑ之间进行拟合,则拟合公式为
kH=37.973 7-0.003 695ϑ2+2.315 1×10-7ϑ4
(28)
当90°≤ϑ≤180°时,参数kH的取值与0°≤ϑ≤90°对应的取值对称。
kH的理论值分布曲线与拟合公式计算值的比较如图6所示。

图6 kH值的拟合Fig. 6 Fitting curve of parameter kH
由图6可得:kH的理论值与拟合公式(28)式的计算值高度一致;理论反演值与拟合公式计算值误差的最大值为0.028 31,均值为0.016 88,标准差为0.008 256。
2阶磁场梯度张量的局部模量CHx、CHy、CHz、CHxy、CHxz、CHyz与M、r及ϑ有关,在特殊情况下,当磁偶极子轴线与坐标轴的某个轴相同时,例如为z轴时,则CHz和CHxy仅与M、|r|及ϑ相关,显然在磁场梯度张量定位时更为简便快速,因此,后面分析磁偶极子轴线方向为z轴方向时CHz和CHxy及参数kHz和kHxy,其三维空间分布规律如图7~图10所示。参数kHz和kHxy的具体取值如表2所示。

图7 CHxy的空间分布Fig.7 Spatial distribution of parameter CHxy

图8 kHxy值的空间分布Fig.8 Spatial distribution of parameter kHxy

图9 CHz的空间分布Fig.9 Spatial distribution of parameter CHz

图10 kHz值的空间分布Fig.10 Spatial distribution of parameter kHz
由图7可知,对于相等距离r的测量位置:在0°≤ϑ≤90°时,CHxy先增大、后减少;在ϑ=35°时CHxy取最大值;在ϑ=90°时CHxy取最小值。由图8可知,kHxy的三维分布趋势与CHxy一致。同时,由表2可知,kHxy和r无关,只和ϑ有关。在ϑ=0°时kHxy为24.000 0;在ϑ=35°时kHxy取最大值25.806 7;在ϑ=90°时kHxy取最小值17.492 9。
由图9可得,对于相等距离r的测量位置:在0°≤ϑ≤90°时CHz先减少后增加;在ϑ=0°时Cz取最大值;在ϑ=71°时CHz取最小值。通过图10可知,kHz的三维分布与CHz相同。同时,由表2可知,kHz和r无关,只和ϑ有关。在ϑ=0°时,kHz取最大值29.3939;在ϑ=71°时,kHz取最小值14.967 3;在ϑ=90°时,kHz为15.297 1。
kHxy和kHz与r无关,只与ϑ相关,kHxy和kHz可表示为

表2 kHxy和kHz值的理论反演值Table 2 Theoretical inversion value of parameterskHxy and kHz
kHxy=24.146 6-6.160 4×10-2ϑ+9.320 3× 10-3ϑ2-2.218 8×10-4ϑ3+1.297 4×10-6ϑ4
(29)
(30)
参数kHxy和kHz的理论分布曲线及其和拟合公式(29)式、(30)式的计算值的比较如图11和图12所示。

图11 kHxy值的拟合Fig.11 Fitting curve of parameter kHxy
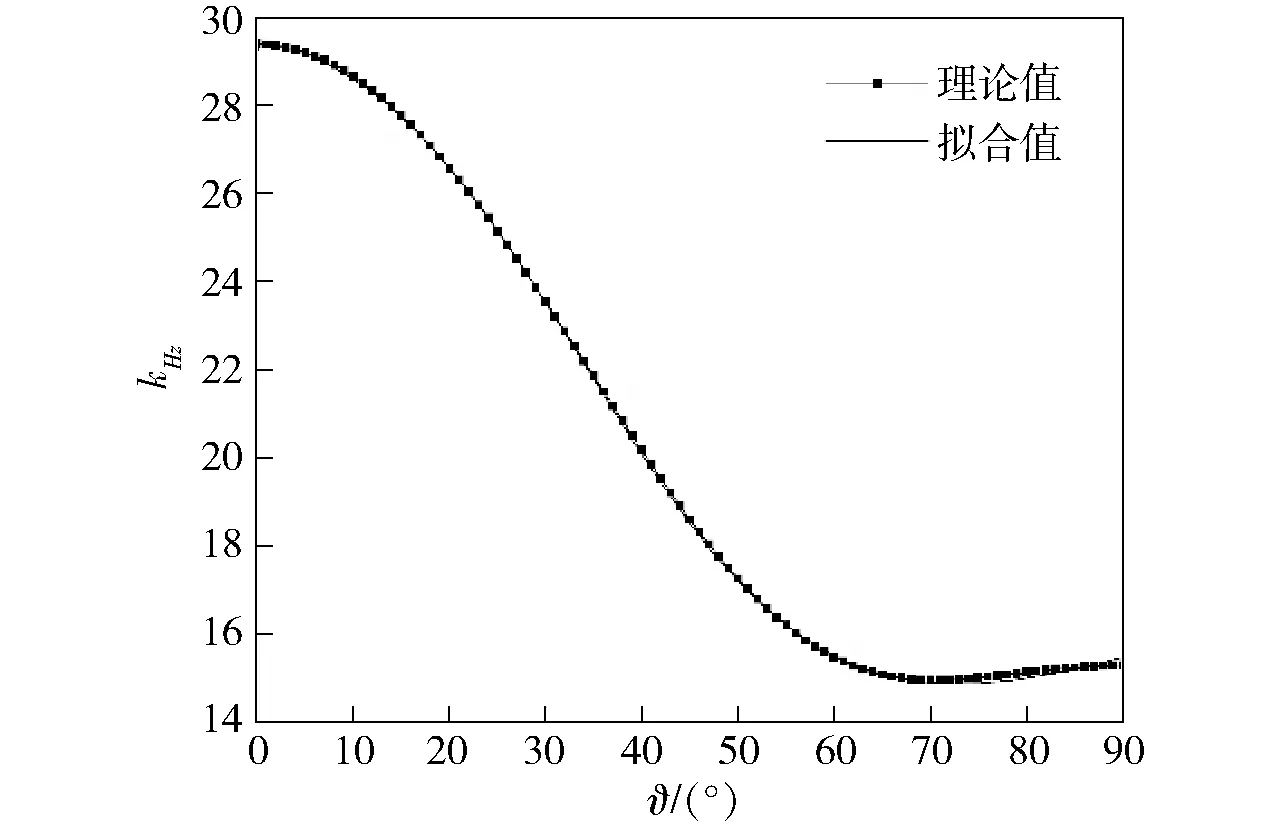
图12 kHz值的拟合Fig.12 Fitting curve of parameter kHz
由图11可得,kHxy的理论反演值与拟合公式(29)式计算值高度吻合;理论反演值与拟合公式计算值误差的最大值为0.146 6,均值为0.032 49,标准差为0.021 36。
由图12可得,kHz的理论反演值与拟合公式(30)式计算值高度吻合;理论反演值与拟合值误差的最大值为0.182 0,均值为0.050 35,标准差为0.039 69。
4 基于磁偶极子的1阶和2阶磁场梯度张量及全局模量与距离的关系
取M=1.0 A·m2,当距离r=0.01 m、0.1 m、1 m、10 m、100 m、1 000 m时,由(2)式和(6)式,可分别计算不同距离情况下的1阶和2阶磁场梯度张量,以Bxx、Bxy和Hxxx、Hxyz为例,进行仿真分析,给出各自的取值范围,比较1阶磁场梯度张量和2阶磁场梯度张量与距离r的规律,结果如表3所示。其中比值范围为max(|Hxxx|)/max(|Bxx|)和max(|Hxyz|)/max(|Bxy|)中取值的最大值和最小值。

表3 1阶和2阶磁场梯度张量与距离的关系Table 3 Relationship between magnetic gradient and distance
由表3可知:
1)当距离从0.01 m增加到1 000 m时,1阶磁场梯度Bxx的范围从±4.13×10 T/m衰减到±4.13×10-19T/m,Bxy的范围从±2.88×10 T/m衰减到±2.88×10-19T/m,Bxx和Bxy与距离的四次方呈反比,与(2)式中1阶磁场梯度和距离的关系一致;2阶磁场梯度张量Hxxx的范围从±1.58×104T/m2衰减到±1.58×10-21T/m2,Hxyz的范围从±9.64×103T/m2衰减到±9.64×10-22T/m2,Hxxx和Hxyz与距离的5次方呈反比,与(6)式中2阶磁场梯度和距离的关系一致。
2)当距离为0.01 m、0.1 m、1 m时,2阶磁场梯度张量的绝对值最大值大于1阶磁场梯度张量,且在距离越小时,2阶与1阶磁场梯度张量的比值越大;即在较小距离时,2阶磁场梯度张量比1阶在数值上更大更敏感;距离越小,2阶磁场梯度张量越敏感。
3)当距离为10 m、100 m、1 000 m时,2阶磁场梯度张量的绝对值最大值小于1阶磁场梯度张量,且距离越大,2阶与1阶磁场梯度张量的比值越小;即在距离较大时,2阶磁场梯度张量比1阶在数值上更小且衰减更快,相对而言,此时1阶磁场梯度张量更敏感。
4)由上所述可知,在磁性物体的探测过程中,如距离较远,则采用1阶磁场梯度张量更灵敏,如距离较近,则采用2阶磁场梯度张量更灵敏;在磁测过程为了消除干扰磁场,当干扰磁场较远时,采用2阶磁场梯度张量更易消除干扰磁场,当干扰磁场较近时,采用1阶磁场梯度张量更易消除干扰磁场。在实际应用时,可结合1阶和2阶磁场梯度张量进行使用,有助于同时提高灵敏度和消除地磁场等干扰磁场。
取M=1.0 A·m2,当距离r=0.01 m、0.1 m、1 m,10 m、100 m、1 000 m时,由(4)式和(14)式进行仿真分析,分别计算不同距离情况下的1阶和2阶磁场梯度张量的全局模量,即CG和CH,给出CG和CH的取值范围,比较1阶和2阶磁场梯度张量的全局模量与距离的关系,结果如表4所示。
由表4可知:
1)当距离从0.01 m增加到1 000 m时,1阶磁场梯度张量的全局模量CG的范围从4.242 6×10~7.348 5×10 T/m衰减到4.242 6×10-19~7.348 5×10-19T/m,与距离的4次方呈反比,与(5)式中1阶磁场梯度张量的全局模量和距离的关系一致;2阶磁场梯度张量的全局模量CH的范围从2.323 8×104~3.794 7×104T/m2衰减到2.323 8×10-21~3.794 7×10-21T/m2,与距离的5次方呈反比,与(21)式中2阶磁场梯度张量的全局模量和距离的关系一致。

表4 1阶和2阶磁场梯度张量的全局模量与距离的关系Table 4 Relationship between magnetic gradient’s full modulus and distance
2)当距离为0.01 m、0.1 m、1 m时,2阶磁场梯度张量的全局模量的最大值大于1阶磁场梯度张量的全局模量,且在距离越小时,2阶与1阶磁场梯度张量的全局模量的比值越大;即在较小距离时,2阶磁场梯度张量全局模量比1阶在数值上更大更敏感;距离越小,2阶磁场梯度张量的全局模量越敏感。
3)当r=10 m、100 m、1 000 m时,2阶磁场梯度张量的全局模量最大值小于1阶,且距离越大,2阶与1阶磁场梯度张量的全局模量的比值越小;即在r较大时,2阶磁场梯度张量的全局模量在数值上比1阶更小且衰减更快,相对而言,此时1阶磁场梯度张量的全局模量更敏感。
4)由上述可知,在磁性物体的探测过程中,当距离较远时,采用1阶磁场梯度张量的全局模量更灵敏,当距离较近时,采用2阶磁场梯度张量的全局模量更灵敏;在磁测过程为了消除干扰磁场,当干扰磁场较远时,采用2阶磁场梯度张量的全局模量更易消除干扰磁场,当干扰磁场较近时,采用1阶磁场梯度张量的全局模量更易消除干扰磁场。在实际应用时,可结合1阶和2阶磁场梯度张量的全局模量进行使用,有助于同时提高灵敏度和消除地磁场等干扰磁场。
由(5)式和(21)式,可得到1阶和2阶磁场梯度张量的全局模量的比值与距离的关系式,即
(31)
由(31)式可知,对于同一个测点(由角度ϑ和距离r确定),若1阶和2阶磁场梯度张量的全局模量相等,则相应的距离r取值如下:
(32)
由于参数kH和kG均仅与ϑ有关,则1阶和2阶磁场梯度张量的全局模量相等时对应的距离也仅与ϑ相关,如表5所示。
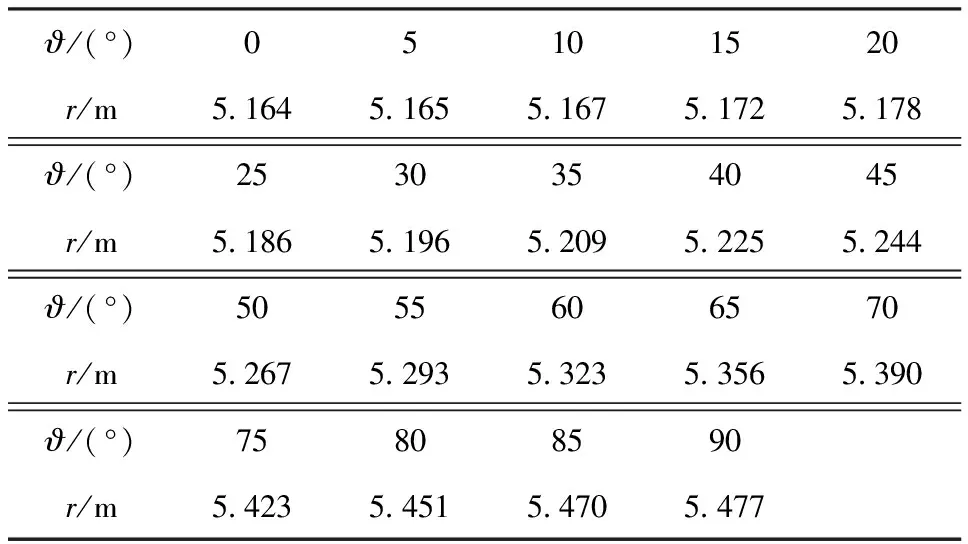
表5 1阶和2阶磁场梯度张量的全局模量 相等时的距离Table 5 Relationship between angle and distance when CG=CH
由表5可得,如1阶和2阶磁场梯度张量的全局模量相等,则距离在5.164~5.477 m之间,具体数值仅与ϑ相关。
由(32)式可知,当距离r
5 结论
1)本文提出了基于磁偶极子的2阶磁场梯度张量缩并方法,探讨了全局模量、局部模量及参数kH的三维空间分布,给出了相关参数kH、kHxy和kHz的近似计算公式,比较了1阶和2阶磁场梯度张量及全局模量与距离的关系。
2)0°≤ϑ≤90°时,全局模量CH及参数kH随着ϑ增大而减小,在ϑ=0°时最大,在ϑ=90°时最小。0°≤ϑ≤90°时,局部模量CHxy和kHxy随ϑ先增加后减少,当ϑ=35°时最大,当ϑ=90°时最小;局部模量CHz和kHz随ϑ先减少、后增加,当ϑ=71°时最小,当ϑ=0°时最大。
3)给出了2阶磁场梯度张量的全局模量和局部模量的计算中相关参数kH、kHxy和kHz的近似计算公式,且理论反演值和拟合值吻合度极高。
4)在距离较近时,2阶磁场梯度张量更敏感,2阶磁场梯度张量及全局模量的取值大于1阶;在距离较远时,1阶磁场梯度张量更敏感,2阶磁场梯度张量及全局模量的取值小于1阶。在实际应用时,可结合1阶和2阶磁场梯度张量的全局模量进行使用。
5)鉴于2阶磁场梯度张量在磁场定位方面的应用价值,2阶磁场梯度张量缩并方法有必要进一步的试验验证。
